Аналитический расчет дифференциальных и интегральных электромагнитных характеристик МГД-перемешивателя

В процессе приготовления многокомпонентных сплавов важной технологической операцией является перемешивание расплава с целью выравнивания химического состава и температуры во всем объеме ванны миксера. Перемешивание расплава в плавильных печах позволяет повысить интенсивность плавления и сократить на эту операцию потребление энергии. Основным достоинством электромагнитного перемешивания признано отсутствие контакта с высокотемпературным и агрессивным расплавом и возможность автоматизировать операцию перемешивания. В металлургической практике наибольшее распространение получили индукционные магнитогидродинамические (МГД) перемешиватели, воздействующие на расплав бегущим магнитным полем. Источником бегущего магнитного поля служит индуктор, представляющий собой катушки, расположенные на магнитопроводе, сдвинутые в пространстве и питаемые m -фазной системой переменных токов. Как правило, электромагнитные, тепловые и гидродинамические процессы в миксерах с МГД-перемешивателями моделируются численными методами с использованием таких программных пакетов, как ANSYS и т.д. [1] На ранней стадии проектирования МГД-перемешивателей требуется выбрать тип обмотки индуктора, количество фаз, частоту питающего напряжения, токовую нагрузку и т.д. Для этого требуется простая методика проектирования этих устройств. В [2] решена одномерная задача анализа электромагнитных процессов в МГД-перемешивателе. Интегральные и дифференциальные характеристики получены при наличии только первой гармоники электромагнитного поля в зазоре. В данной статье аналитически решена двухмерная задача по анализу электромагнитного поля в МГД-перемешивателе с применением рядов Фурье в комплексной форме. Полученные выражения позволяют учитывать тип обмотки, количество и размеры пазов, распределение токовой нагрузки и влияние продольного краевого эффекта.

Расчетная модель системы «МГД-перемешиватель – ванна с расплавом»

Эскиз системы, состоящей из ванны с жидким металлом (расплавом) и индуктора бегущего магнитного поля, представлен на рис. 1.

Индуктор расположен на расстоянии δ от расплава и имеет длину L= 2 pτ , где p – число пар полюсов; τ – полюсное деление.

Для анализа электромагнитного поля примем следующие допущения:

• 1.    Магнитопровод индуктора имеет магнитную проницаемость µ=∞ и электропроводность γ= 0 . В M пазов магнитопровода уложены проводники с током, каждый m -й паз заменен поверхностным током с комплексной линейной плотностью

• 2.    Воздушный зазор равномерный и равен

• 3.    Система имеет бесконечную длину в направлении оси y , т.е. электромагнитное поле является плоскопараллельным. Вектор комплексной напряженности электрического поля E=e y- E y , вектор комплексной напряженности магнитного поля H=e_x-H_x+e z H z , где ё_х , ё_y, ё_z -единичные векторы прямоугольной системы координат.

• 4.    Систему координат считаем жестко связанной с индуктором, а все элементы металла в ванне двигаются относительно индуктора с одинаковой скоростью u .

W I т _ ,vm m m ” 2A , m где wm - число проводников; /m - комплексный ток; 2Аm - ширина m-го паза.

⁸ k s k ^m §, (2) где k δ и k m – коэффициенты, учитывающие влияния пазов и магнитного сопротивления ярма и зубцов соответственно.

При принятых допущениях расчетная модель системы будет иметь вид, представленный на рис. 2.

Дифференциальные уравнения и граничные условия

Решение будем искать для комплексной напряженности электрического поля в области 1 (0 < z < J ) и области 2 ( J < z < да ) E 1 =e_yE_1y; E 2 = e_y-E_2y. .

В расчетных областях справедливы дифференциальные уравнения и граничные условия [3]:

^{d 2} Ey + ^{d 2} E 1 y = ₀. d z ²       d x x      ’

d ² E ₂     d ² E ₂                 .               d E ₂

—^y +      - i • Ц о • Y • ®-^E 2 y - A ) • Y • u^y = 0; ^(3, 4)

о z      о x                             d x

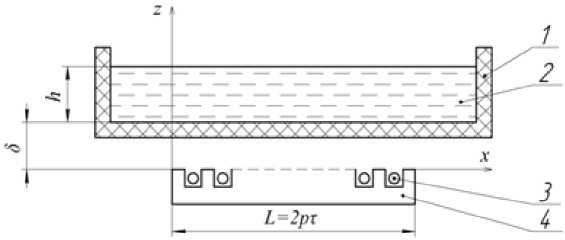
Рис. 1. Индуктор бегущего магнитного поля вблизи ванны с расплавом: 1 – прямоугольная ванна; 2 – расплав; 3 – многофазная обмотка; 4 – магнитопровод индуктора

ц=,х:; y-0

Рис. 2. Расчетная модель МГД-перемешивателя расплава в ванне, x_m – расстояние до центра m -го паза от начала системы координат

Здесь i^-1; ^ о =4- ^п- 1а ^- Гн/м ; m=2- ^nf с^-1; f ^— частота тока, Гц; ^{y —} удельная электропро— водность расплава, 1^/(Ом^м

Комплексная линейная плотность тока J m определяется выражением (2), где

J J е^™ и ™ и e

-

Величина фазы m -го тока зависит от количества фаз, числа пар полюсов p и количества пазов M .

Решение дифференциальных уравнений

Полагая, что электромагнитное поле периодично по координате x с периодом T , будем искать решения в виде рядов Фурье в комплексной форме [4]:

E^(. x , Z ) = z ^ n ( Z )ekx , n =-”	(9)
&                     1 T & E 1,2 n (z ) = T J E 1,2 ( x , z ) e   n d x ;	(10)
kn = ^n ^ -	(11)

Умножив уравнения (3) и (4) на функцию e ^-iknx и проинтегрировав получившееся выражение по x от 0 до T , получим:

d 2 E 1 n dz 2	kn 2 E & 1 n	= 0;	(12)
d 2 E & 2 n	ϕ n 2 E & 2 n	= 0;	(13)
dz 2
ϕ n 2 = k n	2 + i ⋅ µ 0	⋅ γ ⋅ ω + i ⋅ k n ⋅ µ 0 ⋅ γ ⋅ u .	(14)

Общие решения обыкновенных дифференциальных уравнений (12) и (13) определяются выражениями

E 1 n = A 1 e ^knz + A 2 e ^{- knz} ;

E 2 n = A 3 e ^{ϕ nz} + A 4 e ^{- ϕ nz} .

(15, 16)

Постоянные интегрирования Aj ( j=1..4) определяются из граничных условий (3-5), которые также необходимо преобразовать в соответствии с (10). При этом условие (3) заменяется выражением dE1n

dz

^ψ n ^,

Определив постоянные интегрирования из граничных условий и подставив их в (15) и (16),

получим:	ϕ n ( δ - z ) E & 1 n = - ψ n Gn ( z ) ;               E & 2 n = - ψ n e      ,                       (19, 20) k n   Q n                            Qn
где	Gn ( z ) = kn cosh ( kn ( z - δ ) ) - ϕ n sinh ( kn ( z - δ ) ) ;                                (21) Q n = k n sinh( k n δ ) + ϕ n cosh( k n δ ).                                           (22)

В соответствии с (6) запишем искомые решения:

где

E & 1 y ( x , z ) =- i 2 ω T µ 0 n ∑=-∞ k 1 2 GQn ( n z ) C 1 n e ik n x ;                                     (23) ” 1 e ^ ^ - z ) E 2 y ( x”' ) = ‘ T : k ,    Q n   Cl n e  ;                               (24) M C 1 n = : Jm sin( k, A m ) e-knxm -                                               (25) m = 1

Из уравнения Максвелла rotE =-гю В, имеем:

■     1 d Ey                       .     1 d Ey Bx = ■ я ;                      Bz = ■ я ;                                 (26) i m d z                         i rn d x

Подставив (23) и (24) в (26), получим:

где

B _ _ 2 , X G' , ( z ) C e k n x .        B _ i 222 у ± G , ( z ) C e k n x .      (27 28) x l        Tn _ _ . k-   Qn     ln    ■          z l       T"k- Q-    "    '          ■ B & x 2 = ^ ^ 0 :: S^e^ C l- е*-;      B z 2 -i"-^ 1L ± e ^^ C i- e-;   (29, 30) T n - _ ” kn   Qn                             T n - _ ” kn   Qn G' n ( z ) = k n smh ( k n ( z - 6 )) - Ф п cosh ( k n ( z - 6 ))                               (31)

Плотность тока в области 2 определяется законом Ома с учетом движения расплава со скоростью u относительно системы координат:

^ Фп ( 6 - z ) 62y = Y(E2 + uB&2z) = i 2П X e—Cnn^(s)ekn;                       (32) T n=-„ nQn (      T т в( s) = Eu (1 -s)-y 1,                                                 (33) где е = юу/^т2 / п2; T* = T / т.

Интегральные и дифференциальные характеристики МГД-перемешивателя

Комплексная электромагнитная мощность, отдаваемая обмоткой индуктора в зазор, равна

• S-    =-1. £ mfE( Х0 - J-., dx     T' £/ GQ0 C_C , n,(34)

д 2.   == m ( . m)     ; S р ДУ р

Электромагнитная сила, действующая на обмотку индуктора в направлении движения, равна силе, действующей на расплав, и определяется выражением

M x m + ^A m &

^Fem = Re ^- S Z J B 1 z ^{( X} ,^{0) J}m ^d x . m = 1 x m — A m

= Re J , 4 ^ > S у Л G^ CC 2               1 ⁿ

I ^T . =-« k -     Q .

.

При взаимодействии магнитного поля с индуктированными в жидком металле токами возникают электромагнитные силы, средняя за период объемная плотность которых описывается выражением f = ReS2 R B2 )= e-f. + e.f.■

где f. = Re{S2 yB 2.}

f z =- Re{< & ₂ y B 2 . }.                       (37, 38)

Запишем выражения для относительных электромагнитной мощности и силы. За базисные мощность и силу примем величины, определяемые выражениями

P b =           J ^1;              F b = 2P7 - ^ 0 - S ■   2 ,             ⁽³9, 40)

^M где J ₌ ^ -m-m .

m = 1 ^T

В соответствии с (34), (36), (39) и (40) будем иметь:

e Srn^-TtL

S em т-x i / v P s     4 n . =-^.

/V

1 G n (0)

3 A n3  Qn

(T¹                         ]

Cl-C2- ;    F⁷m = Fem = Re ] — Z-2- . M C1 -C2 - [ ,  (41^, 42)

F s      | ^{2 n -} =^-» n   Q.         J

где G . (0) = k . cosh ( k . ( . - S )) - ф . sinh ( k . ( . - S )); Q . = k . sinh( k . S ) + q> . cosh( k . S );

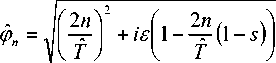
MM

C =Yj sin(£ A >-k; C, =yj sm(k A >k 1n         m       n m             2n         mn m m=1

: _ ^T_k 2nn. t-T- j Jm^- j* -J* n = П ^кп = Г T = T ’ ^J m = J ’ ^Jm = J -

Относительные активная и реактивная мощности соответственно таковы:

Pem = Re{L }               Qem = Im^em |

Коэффициент мощности МГД-перемешивателя и электромагнитный коэффициент полезного действия устройства в двигательном режиме:

ˆˆ cosф = Pem „   ;          Пет = Fey (1 -»).                      (45, 46)

A P em ² + Q em '                 ^P m

Анализ расчета электромагнитных характеристик

Как следует из полученных выражений, безразмерные характеристики индукционного МГД-перемешивателя определяют следующие параметры:

• 1.    Количество пазов M , размеры пазов 2 Δ m и их расположение x m , амплитудно-фазовые характеристики синусоидальных токов в пазах J_m=Jmei*™, соотношение размеров индуктора ( L =2 p т=2т) и ванны (Т =Т/т ).

• 2.    Безразмерный коэффициент добротности E=Ym^₀T2 /П .

• 3.    Относительная величина зазора между индуктором и расплавом – δ/τ.

• 4.    Скорость движения расплава (как твердого тела) относительно индуктора – u или величина скольжения s =1- u / τ f . Для упрощения сравнения характеристик будем полагать, что ширина всех пазов одинакова (Δ _m=const ) и они занимают половину длинны индуктора, т.е. Е M=1 2 А _т=т .. Условие T =2т позволяет анализировать электромагнитное поле и электромагнитные характеристики без учета влияния продольного краевого эффекта. Рассмотрим три типа обмоток (рис. 3): трехфазная обмотка с фазной зоной 120° (рис. 3 a ); двухфазная обмотка с фазной зоной 90° (рис. 3 б ); трехфазная обмотка с фазной зоной 60° (рис. 3 в ). Очевидно, что линейная токовая нагрузка во всех трех вариантах обмоток одинакова.

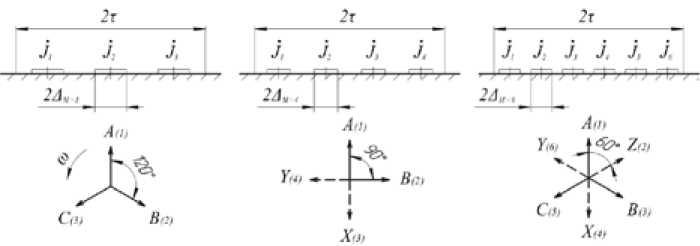
a                           б                          в

Рис. 3. Исследуемые типы обмоток индуктора

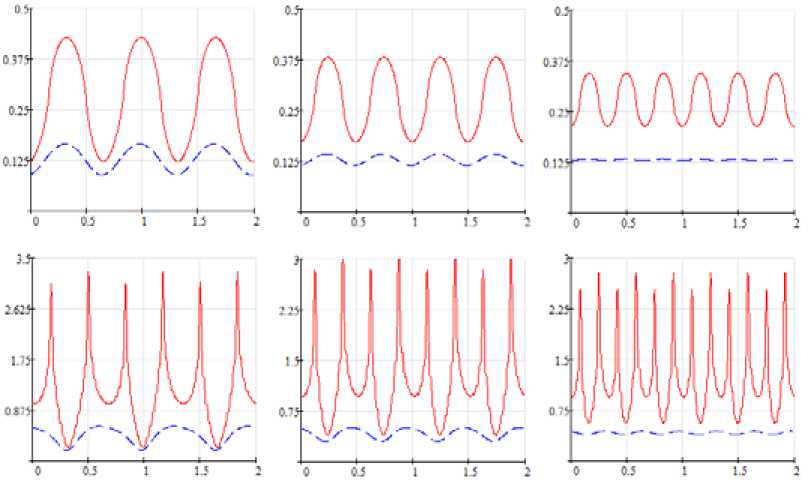
a                            б                              в

Рис. 4. Относительная напряженность электрического поля и нормальная составляющая относительной магнитной индукции для трех вариантов обмоток

На рис. 4 представлены огибающие кривые относительной напряженности электрического поля ( E 1y / to^ 0 jT ) и нормальной составляющей относительной магнитной индукции ( B 1z /pJ на поверхности индуктора ( z=0 ) – сплошные линии – и поверхности расплава ( z=δ’ ) – пунктирные линии. По оси абсцисс показаны относительные значения. Кривые, представленные на рис. 4 a , 4 б , 4 в , соответствуют обмоткам на рис. 3 a , 3 б , 3 в . При расчете принималось T= 2 τ ; s= 1; δ/τ= 0,2; ε= 2, т.е. скорость расплава u=0 . Если на поверхности индуктора зубцово-пазовые гармоники явно проявляются, то на поверхности расплава их проявление ослабевает. При этом с увеличением числа пазов проявление гармоник также уменьшается.

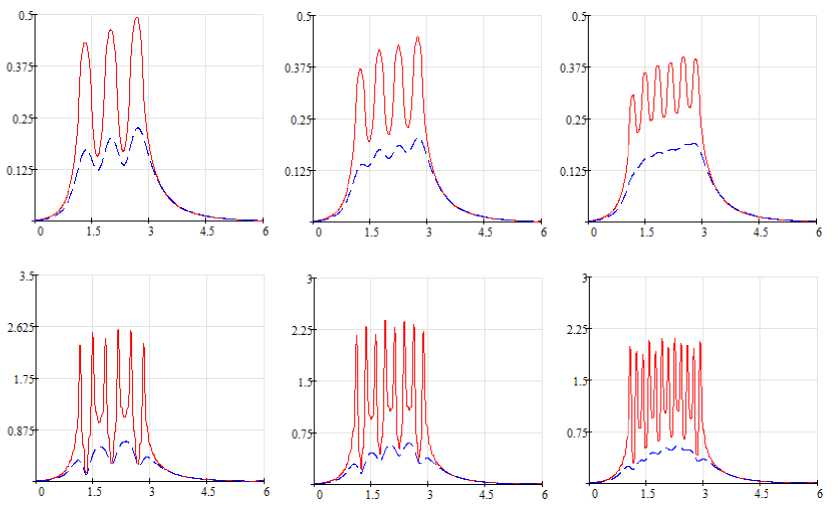
Картина распределения электромагнитного поля изменяется при наличии движения расплава относительно индуктора ( u≠0 ). На рис. 5 показаны те же огибающие при наличии движения. При расчете принималось T= 6 τ ; s= 0,1; ε= 2; δ/τ= 0,2. От начала координат до входа в индуктор предусмотрено расстояние τ , а от выхода индуктора до конца периода T – расстояние 3 τ . Вследствие проявления продольного краевого эффекта на входе индуктора электромагнитное поле сжимается, а на выходе вытягивается. Неравномерность распределения электромагнитного поля по длине индуктора приводит к несимметрии токов в фазах при их подключении к источнику фиксированного напряжения. С уменьшением зазора δ неравномерность возрастает.

На рис. 6 и 7 представлены интегральные характеристики, соответствующие рассматри-;

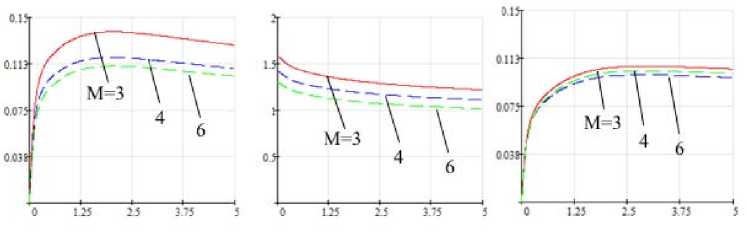
ваемым обмоткам. Зависимости относительных активной Р_ет и реактивной Q_em мощностей от ε при M=3, 4, 6, показаны на рис. 6 a и 6 б соответственно. На рис. 6 в показана зависимость cos ф = f(E).

a                           б                           в

Рис. 5. Относительная напряженность электрического поля и нормальная составляющая относительной магнитной индукции для трех вариантов обмоток при T≠2τ и s= 0,1

а                           б                            в

Рис. 6. Относительные активная (а), реактивная мощности (б) и коэффициент мощности от ε (в)

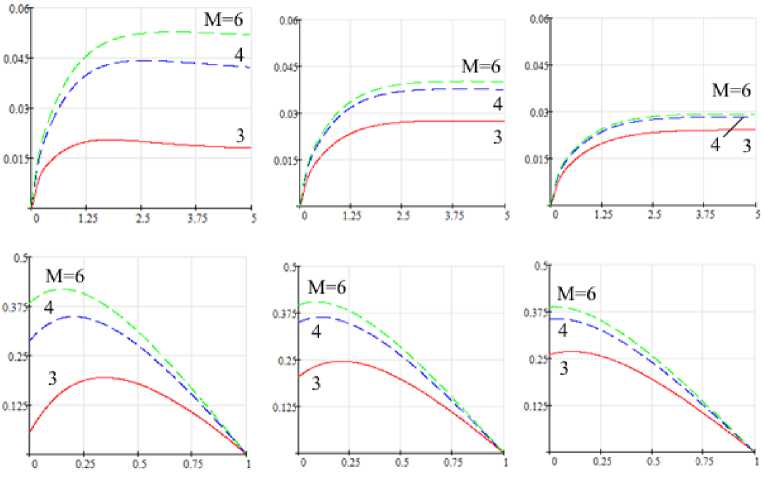
На рис. 7 а изображены зависимости относительной электромагнитной силы F_m от добротности ε , а на рис. 7 б представлены зависимости коэффициента полезного действия η от скольжения s .

Как следует из представленных графиков, индуктор с трехфазной обмоткой с фазной зоной 120° ( M =3) потребляет из сети бóльшие активную и реактивную мощности, чем индуктор с обмотками M =4 и 6. Вместе с тем индуктор с этой обмоткой развивает электромагнитную силу F_em , действующую на расплав, меньшую, чем индукторы с другими обмотками (рис. 7 a ). Этому соответствуют графики η= f ( s ), представленные на рис. 7 б . С увеличением величины – 82 –

б                                в)

Рис. 7. Относительная электромагнитная сила от ε (сверху), КПД от s (снизу): а – δ/τ =0,2; б – δ/τ =0,3; в – δ/τ =0,4

зазора ( δ/τ от 0,2 до 0,4) разность электромагнитных характеристик представленных обмоток уменьшается.

Выводы

На основе использования интегрального конечного преобразования с использованием рядом Фурье в комплексной форме решена двухмерная задача по анализу электромагнитных процессов в системе «МГД-перемешиватель – ванна с расплавом». Полученные выражения для дифференциальных характеристик: векторов электромагнитного поля, плотности тока и удельных электромагнитных сил в расплаве, позволяют анализировать гармонический состав электромагнитного поля в зазоре при различном дискретном распределении токовой нагрузки в индукторе и с учетом проявления продольного краевого эффекта. Выражения для электромагнитных мощности, силы, коэффициентов полезного действия и мощности дают возможность оценить требования к источнику питания МГД-перешивателя и эффективность его работы.

Проведен анализ дифференциальных и интегральных характеристик МГД-перешивателя с распространенными типами двухфазной и трехфазной обмотками, показаны их зависимости от коэффициента добротности и количества пазов индуктора.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда поддержки научной и научно-технической деятельности в рамках научных проектов № 16-48-242018 и № 16-43-242013 р_офи_м.