Аналитический расчёт преломляющих оптических элементов для формирования однопараметрических диаграмм направленности

Задача формирования заданных диаграмм направленности (ДН) излучения актуальна для ряда прикладных задач, включающих создание оптических элементов для светотехнических систем различного назначения. В общем случае для формирования ДН заданной формы требуются преломляющие или отражающие оптические элементы с поверхностями свободной формы. Как правило, для расчёта таких оптических элементов используются итерационные методы [1 –7]. Итерационные методы имеют ряд недостатков (вычислительная сложность, эффекты стагнации, не гарантируется сходимость к глобальному оптимуму) и далеко не всегда позволяют получить решение.

На взгляд авторов, наиболее естественным представлением поверхности свободной формы для формирования заданной ДН в виде двумерной области или кривой является огибающая поверхность. При этом отражающая поверхность представляется в виде огибающей параметрического семейства параболоидов вращения [8, 9], а преломляющая поверхность – в виде огибающей гиперболоидов или эллипсоидов вращения, в зависимости от показателей преломления сред, разделяемых поверхностью [10– 12]. Указанные поверхности позволяют преобразовать сферический пучок света от источника в коллимированный пучок заданного направления. Такой подход ранее использовался авторами для расчёта отражающих и преломляющих оптических элементов, формирующих однопараметрические ДН (диаграммы направленности в линию) [8– 12]. При сферическом освещающем пучке законченные аналитические решения были получены только для случая формирования ДН в виде отрезка прямой [9, 11]. В этом случае расчёт зеркала (или преломляющей поверхности) был сведён к интегрированию обыкновенных дифференциальных уравнений, разрешённых относительно производной. В случае однопараметрической ДН произвольного вида формирование заданного распределения энергии на ДН требует решения сложного нелинейного дифференциального уравнения второго порядка.

В настоящей работе рассмотрен расчёт преломляющих оптических элементов для формирования заданных однопараметрических ДН в важном частном случае освещающего пучка с плоским волновым фронтом. В данном случае расчёт преломляющей поверхности при произвольной форме ДН удалось свести к последовательному решению двух дифференциальных уравнений первого порядка, разрешённых относительно производной. В качестве примера рассчитаны оптические элементы, формирующие ДН в виде отрезка, дуги окружности и двух дуг окружностей.

Расчёт преломляющей поверхности

Пусть освещающий пучок с плоским волновым фронтом и направлением распространения e _z = (0, 0, 1) падает на преломляющий оптический элемент (рис. 1).

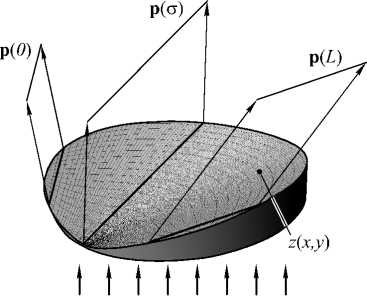
Рис. 1. Геометрия задачи формирования ДН

Показатели преломления материала элемента и окружающей среды составляют n1 и n2 соответственно. Первая поверхность оптического элемента является плоской и расположена в плоскости z =0 при (x, y) e G , где G - апертура элемента. Вторая поверхность оптического элемента описывается функцией z = z (x, y), (x, y) e G . Отметим, что при указанной геометрии оптического элемента преломление падающих лучей происходит только на второй поверхности. Задача состоит в расчёте формы преломляющей поверхности z(x,y) из условия, что направления преломлённых лучей описываются заданной единичной векторной функцией одного аргумента

p ( ° ) = ( P x ( ° ), P y ( ° ), P z ( ° ) ) , |p(°)| = 1, (1) где °e [0, d ] - некоторый параметр. Следуя работам [8-12], будем называть функцию (1) диаграммой направленности в виде линии. Дополнительно на ДН (1) должно быть сформировано заданное распределение энергии, описываемое функцией I ( ° ), °е [0, d ].

Рассмотрим сначала вспомогательную задачу, состоящую в расчёте плоской преломляющей поверхности, преобразующей освещающий пучок с плоским волновым фронтом и направлением e ₀ (| e ₀ | = 1) в пучок с плоским волновым фронтом и направлением p ( ° ), где ° - некоторое фиксированное значение параметра. Обозначим n ( ° ) - нормальный вектор плоской преломляющей поверхности. Согласно закону преломления (закону Снеллиуса) вектора e ₀ , p ( ° ), n ( ° ) лежат в одной плоскости. Таким образом, мы можем представить вектор n ( ° ) в виде линейной комбинации векторов е ₀ и p ( ° ):

^{n (} ° ) = C 1 p ( ° ) + С 2 ^e 0 , ⁽²⁾ где c 1 , c ₂ - некоторые коэффициенты. Умножив левую и правую части выражения (2) векторно на n ( o ), будем иметь:

c1 sin (apr)+ c 2 sin (a0) = 0, где a0 и apr - углы падения и преломления соответственно. Поскольку sin (a0) / sin(apr)= n21 = n2 / n1, то получим

n ( ° )~ 6 0 - n 21 Р ( ° ). (3)

Уравнение (3) является решением простейшей обратной задачи, состоящей в определении нормального вектора плоской преломляющей поверхности по заданному направлению p ( ° ) преломлённого пучка.

Рассмотрим освещающий пучок с плоским волновым фронтом и направлением распространения e ₀ = e z = (0,0,1). В этом случае уравнение преломляющей плоской поверхности может быть получено из (2), (3) в виде:

z - n 21 (p(°), M ) = V(°), (4) где M = (x, y, z), а функция y(°) характеризует расстояние от преломляющей плоскости до начала координат. Преломляющую поверхность для формирования заданной ДН (1) предлагается определить в виде огибающей семейства плоскостей (4) по параметру о. По определению, огибающая поверхность касается каждой из плоскостей семейства (4) вдоль некоторой кривой. Поскольку направления нормалей огибающей поверхности и плоскостей (4) вдоль кривых касания совпадают, то преломлённые лучи будут иметь заданные направления (1). Таким образом, расчёт преломляющей поверхности для формирования ДН (1) сводится к построению огибающей для семейства плоскостей (4). Уравнение огибающей поверхности в декартовых координатах имеет вид [13]

[ z - n21 (p (°), M) = V(°), ifdp(°) m)-   1 dV(°)                    (5)

I            , M- I = .

[( d°     )    n21 d°

Первое уравнение в (5) является уравнением исходной плоскости, а второе уравнение соответствует производной первого уравнения по параметру о и также является уравнением плоскости с нормальным вектором d p ( ° ) / d ° . Таким образом, огибающая поверхность образована из прямых Г ( ° ), являющихся пересечением плоскостей в (5). В математике такие поверхности называются развёртывающимися.

Функция v(°) в (5) определяет распределение энергии вдоль ДН. Рассмотрим расчёт v(°) из условия формирования заданного распределения энергии на ДН. Согласно (5), направляющие вектора прямых Г(°), образующих огибающую поверхность (5), имеют вид:

X d p ( ° ) t ( ° ) = n ( ° ) X ' d °

.

где n ( ° ) = ( p_x ( ° ), p y ( ° ), p_z ( ° ) - 1/ n ₂₁ ) — нормальный вектор плоскости в (4). В общем случае t_z (о) ^ 0 и прямая с направляющим вектором (6) пересечёт плоскость z = 0. Полагая z = 0 в (5), получим для нахождения точки пересечения ( x 0 , y 0 ), расположенной в плоскости z = 0, следующую систему линейных уравнений:

P x ( ° ) X 0 + P y ( ° ) У 0 =-- V ( ° ), n ₂₁

' *X° x + ^Py*°l y = d° 0    d°   0

-

1 d ^ ( ° ) n 21   d °

.

Решая систему (7) с использованием правил Крамера, получим:

. x ⁰

-

У 0 =

-

^{f d} P y ( ° ) , . d y ( o ) ) I — y— y ( o) — P_y ( о ) I , ( d a d a y )

f . ,dv ( ° ) d P _x ( ° ) ) - Px ю' —-x — v ( ° ) , 1 1 d ° d ° )

I n 21 t z ( ° ) I

1 . _________________________________ n 21 t z ( ° )

,

где tz (°) = Px (°)

^d P y ( ° ) d °

-

d P ( ° ) Py ( ° ) , ^y     d °

.

Обозначим т(о) единичную проекцию вектора t(o) в (6) на плоскость z = 0. В этом случае проекция Г± (°) прямой Г(°) на плоскость z = 0 может быть записана в виде:

(x-x0)тy(°)-(y-y0)тx(°) = 0 , или xтy (°) - yтx (°) = l(°) , где

l ( о ) = x 0 ( О ) т у ( о ) - У 0 ( о ) т x ( о ) =

= ---1— [ ^^ ( P x ^{( О ) Т} X ^{( О ) +} Р у ^{( О ) Т} у ^{( О )} ) ^{- (10)}

n ₂₁ t z ( o ) V do ^х                   y ^у *

Без ограничения общности будем считать, что падающий пучок имеет радиально-симметричное распределение освещённости:

, х Г d p ( о) , х d Р у ( о )      ))

-V(o)l— X — т x ( о ) + — У — т у ( о ) I .

V d o           d o    ^у )J

Далее рассмотрим случай t z b) = 0. Этому условию, в частности, соответствует ДН в виде «отрезка», заданная уравнением p ( o ) = ( p_x ( o ),0, p z ( o )). Для указанной ДН вектор t (o) в (6) перпендикулярен плоскости XOZ и проекции Г _± (о) имеют следующий простой вид:

E 0 ( x , у ) = E 0 ( р ) , р = V x ² + у ²<  R ,             (14)

где R - радиус пучка. Отметим, что функция l ( о )

равна расстоянию от прямой Г_± ( о ) до начала координат в плоскости z = 0. Поэтому при условии (14) закон сохранения светового потока можно записать в следующей дифференциальной форме:

x = l ( o ).

При условии (11) из (5) несложно получить, что

f ^/ R m^O)

J ___ E 0 ( V l ² (^o) ⁺ t ² ) ^d t ^d l (^o) = I (^o)

- V R ² - l ² (o)

d p ( o ) d o

d o ,

— 1

l(o) = . / х-------,      

^P, ° + n 21 ^T^P x ^{( o )/} ( 1 ^- n 21 P z ^{( o )} )

do        do f 1 dy(o)     у (o)   dPz (o)

Xl---1

n ₂₁   d o     1 - n ₂₁ p z ( o )  d o

.

Таким образом, функция l ( о ) в (10), (12) определя

ется функцией у ( о ) и её производной. Рассмотрим расчёт функции l ( о ) из условия формирования заданного распределения энергии I ( o ), ое [0, d ] вдоль ДН. Следуя работам [12, 14], функцию I ( о ) будем называть линейной плотностью энергии. Данное название связано с определением I ( o ) как интегральной величины,

или dl^L I(o) dp^0)/ У E0 (l2 (o)+t2)dt. (15) do               do         .-.       '               *

- R - l ( σ )

Таким образом, расчёт функции l ( o ) сводится к интегрированию обыкновенного дифференциального уравнения первого порядка, разрешённого относительно производной. Решение уравнения (15) является тривиальной задачей, которая может быть решена с использованием стандартного метода Рунге-Кутты.

Пусть ое [0, d ] является натуральным параметром,

при этом

^d P ^{( o )} d o

= 1. В важном частном случае, соответ-

которая соответствует световому потоку, попадающему на единицу длины ДН. Для получения заданной линейной плотности I ( о ) определим функцию l ( о ) из закона сохранения светового потока. Для этого приравняем световой поток падающего пучка, заключённый между начальной прямой Г_± (0), касающейся апертуры опти

ствующем постоянной освещённости падающего пучка E ₀ ( р ) = E ₀ , р< R и постоянной линейной плотности I ( о ) = I , ое [0, d ], уравнение (15) может быть решено аналитически относительно функции o( l ) в виде:

ческого элемента, и текущей прямой Г_± ( о ) , к световому потоку, проходящему через фрагмент ДН, заключённый между направлениями p (0) и p ( o ) :

d

o ( l ) = — arcsin п

V

l I l 1 + 1

R 7 Ry

-

х 2

l 1

R 7

d

+--.

σ

J I ( t )

d p ⁽ t ) d t

d t = J   E ₀ ( x , у ) d x d у ,

D ( 0, 0 )

где E ₀( x , у ) - освещённость падающего пучка в плоскости z = 0, D (0, о ) - область, заключённая между

прямыми линиями Г_± (0) и Г_± ( о ) .

d y ( o ) d o

Соответственно, функция l ( o ) получается из решения уравнения (16).

Уравнения (5), определяющие преломляющую поверхность, зависят от функции у ( о ) и её производной. Данная функция при известной функции l ( o ) может быть вычислена из уравнений (10) и (12) (в зависимости от условий t z ( о ) ^ 0 или t z ( о ) = 0) в виде:

1 I X        \7 d P x ( o )          ^d P y ^{( o )}

---------------------- n ₂₁ t z ( o ) l ( o ) +y ( o ) l — ^x —- т _x ( o ) +— ^у — т, ( o ) P x ( o ) т x ( o ) + P y ( о ) т у ( о ) V                   V d o             d o ^у

= 5

- n „ 1 1 ( o ) I ^{J p ,o)} + n Il d o

d P z ( О ) P x ( О ) I + y ( o ) d P z ( o )

21      1                           x do  1 - n21 pz (o)

^{1 -} n 21 Pz ^{( О )  d O}   J ,

tz (о) ^ 0, tz (О) = 0.

Согласно (17), расчёт у ( о ) также сводится к интегрированию обыкновенного дифференциального уравнения первого порядка, разрешённого относительно производной.

Таким образом, расчёт преломляющей поверхности для формирования заданной ДН p (o) сводится к интегрированию дифференциальных уравнений (15), (17) с последующим восстановлением профиля по-

верхности из уравнений (5), (9). В частности, при τ _y (σ) ≠ 0 уравнение огибающей поверхности несложно

получить в следующем аналитическом виде:

z I CT , y ) =

---------X

¹ - n 21 P z ^{( CT )}

, .           , . l ( CT ) + y T ( CT )

X _V ( o ) + n 21 p_x ( ст)-----—

I                          T ( CT )

J

+ n 21 P y ( CT ) y .

J

вещённостью E 0 ( x , y ) = E 0 , ^/ x ² + y² <  R . ДН определим как направления на точки кривых, расположенных в удалённой плоскости z = f , f >>  R . Запишем уравнения кривых, расположенных в плоскости z = f и соответствующих отрезку, дуге окружности и композитной кривой, состоящей из двух дуг окружностей:

В частном случае задачи формирования ДН в виде отрезка ( p ( CT ) = ( p_x ( ct ),0, p_z ( ст )) ) преломляющая по-

X seg ( ct ) = I -^ + ct ,0, f J , сте [ 0, d ] ,             (20)

верхность соответствует цилиндрической поверхности:

X (g) = 7? x arc               arc

Z ( CT ) =  ------ '       ( v ( CT ) + n 21 P x ( CT ) l ( CT ) ) .          (19)

^{1 -} n 21 P z ^{( CT )}

X sin

I

f CT- d /2 J

R arc

cos

f ст- d /2 J

R arc

-

R 0

f

A

R arc

,

R arc J

,

Примеры расчёта преломляющих оптических элементов

Были рассчитаны оптические элементы, формирующие ДН в виде отрезка, дуги окружности и двух дуг окружностей, при освещающем пучке с постоянной ос- сте [0,d],

^X comp (^CT) = ^R arc

fr

^{- sin}

I sin

.I

f ст- d /2

R arc ст-d/2 J

R arc

f CT- d /2

, - cos --------

R arc

f CT- d /2 cos I----------

R arc

-

f

A

1    /                rx d

⁺‘t 0'4 ,

R

/ arc J L

1 f ^J Г d j

1, R ^CT i, d ,

“arc J

d

где d – длина отрезка в (20), длина дуги окружности в (21) и длина композитной кривой в (22), R arc – радиус дуг окружностей в (21), (22), φ_arc= d / R _arc – угловой размер дуги в (21), φ_arc /2 – угловые размеры дуг в (22). Согласно (20)–(22), соответствующие ДН имеют вид:

Pseg (CT) = Xseg (CT) /|Xseg (ct)| ,(23)

Parc (CT) = Xarc (ct) / |Xarc (ct)| ,(24)

Pcomp (CT) = Xcomp (CT) / |Xcomp (CT)| .

Расчёт оптических элементов для формирования ДН (23)–(25) производился по формулам (15), (17)– (19) при следующих параметрах: радиус освещающего пучка R = 20 мм, f =5000 мм, d = 3000 мм, ф arc = 70°, показатель преломления материала элемента n ₁ = 1,5, показатель преломления окружающей среды n ₂ = 1. При расчёте оптических элементов функции линейной плотности энергии были определены в виде I (σ)~1/ p_z (σ). В этом случае оптические элементы будут формировать в удалённой плоскости z = f постоянные распределения освещённости вдоль кривых (20)–(22). Рассчитанные оптические элементы приведены на рис. 2 а–в . Отметим, что нижние поверхности элементов соответствуют плоскостям, перпендикулярным падающему пучку. Излом поверхности элемента на рис. 2 в в центральном сечении объясняется тем, что вектор кривизны кривой (22) в точке σ = d /2 меняет знак.

Расчётные распределения освещённости, формируемые элементами на рис. 2, приведены на рис. 3.

Распределения освещённости на рис. 3 были рассчитаны с использованием программы для светотехнических расчётов TracePro [15]. Результаты моделирования показывают высокое качество формирования заданных ДН и подтверждают корректность приведённых математических выкладок.

Заключение

Получено общее представление преломляющей поверхности для формирования однопараметрической ДН в виде огибающей семейства плоскостей при освещающем пучке с плоским волновым фронтом. Расчёт поверхности оптического элемента при произвольном виде ДН сведён к последовательному решению двух дифференциальных уравнений первого порядка, разрешённых относительно производной. Рассчитаны оптические элементы для формирования ДН в виде отрезка, ДН в виде дуги окружности и композитной ДН, состоящей из двух дуг окружностей. Результаты моделирования работы рассчитанных элементов показывают высокую эффективность предложенного метода. Метод может быть обобщён на случай падающего пучка с произвольным волновым фронтом. В этом случае вместо первой плоской поверхности элемента следует использовать преломляющую поверхность, преобразующую падающий пучок в пучок с плоским волновым фронтом.

Работа выполнена при поддержке грантов РФФИ 13-07-97001, 14-07-00339, гранта поддержки ведущих научных школ НШ-3970.2014.9 и Министерства образования и науки РФ.

a)

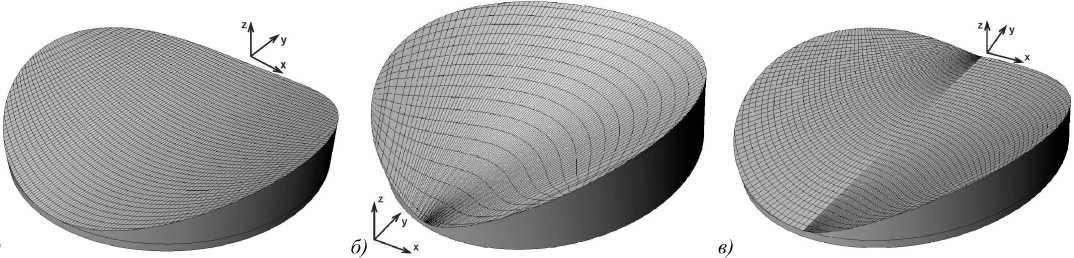
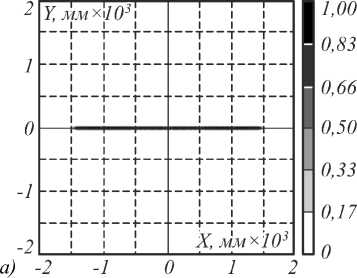
Рис. 2. Оптические элементы (n1=1,5; n2=1) для формирования ДН в виде отрезка (a), ДН в виде дуги окружности (б) и композитной ДН, состоящей из двух дуг окружностей (в). Радиусы элементов равны 20 мм, а максимальная высота составляет 7 мм (a), 9,8 мм (б) и 6,4 мм (в). Параметры формируемых ДН в плоскости z=5000 мм: длины кривых – 3000 мм, угловой размер дуги окружности – 70°, угловые размеры дуг композитной ДН – 35°

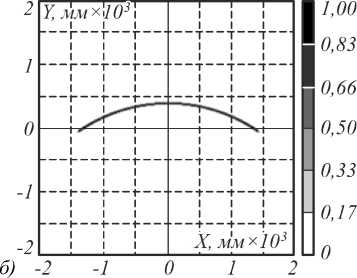
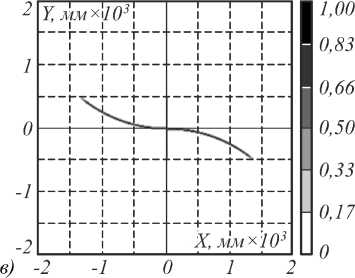
Рис. 3. Распределения освещённости, формируемые оптическими элементами, приведёнными на рис. 2, в плоскости z = 5000 мм