Аналитический расчёт преломляющих оптических элементов для фокусировки в кривую

Задача фокусировки светового пучка в кривую актуальна для широкого круга прикладных областей, включающего лазерные технологии, оптическую обработку информации, микроскопию, светотехнику. Простейшая оптическая система для фокусировки плоского пучка в отрезок соответствует комбинации цилиндрической и сферической линз. Однако при использовании такой системы трудно получить линию высокого качества с требуемым распределением освещённости вдоль линии. Линии произвольной формы с требуемым распределением освещённости могут быть сформированы оптическими элементами с поверхностями свободной формы. Расчёт таких оптических элементов, как правило, основан на сложных оптимизационных процедурах [1–9] (исключением являются задачи с радиальной и цилиндрической симметрией и точечным источником излучения [10, 11]). Рабочие характеристики существующих итерационных процедур являются недостаточно хорошими, и задача расчёта преломляющих (отражающих) оптических элементов для точного формирования сложных распределений освещённости остаётся актуальной.

В работе [6] предложен «метод вспомогательных параболоидов» для расчёта зеркал с поверхностями свободной формы, предназначенных для формирования дискретных распределений интенсивности (освещённости), соответствующих набору точек. В этом случае поверхность зеркала представляется в виде набора сегментов параболоидов или эллипсоидов с определёнными параметрами. Расчёт параметров параболоидов (эллипсоидов) осуществляется итерационным методом, при этом сходимость метода строго доказана [6]. Данный подход был обобщён на случай расчёта преломляющих оптических элементов [7]. В этом случае поверхность оптического элемента состоит из сегментов картезианских ова- лов. В [1, 2, 8, 9, 12] расчёт отражающих и преломляющих поверхностей для формирования непрерывных распределений освещённости основан на построении отображения между угловыми координатами лучей, выходящих из источника, и точками на выходной плоскости. При этом методы [6, 7] используются для определения вида указанного отображения [8].

На взгляд авторов, наиболее естественным представлением поверхности оптического элемента для формирования заданного распределения освещённости в виде двумерной области или кривой является огибающая поверхность. При этом в зависимости от типа оптического элемента (отражающий или преломляющий) поверхность представляется в виде огибающей параметрического семейства эллипсоидов (параболоидов) вращения или картезианских овалов. Такой подход ранее использовался авторами для расчёта зеркал, формирующих однопараметрические диаграммы направленности (диаграммы направленности в виде линий) [13-15]. В этом случае поверхность зеркала соответствует огибающей однопараметрического семейства параболоидов вращения (направления осей параболоидов определяются заданной диаграммой направленности). В важном практическом случае формирования диаграммы направленности в виде отрезка расчёт зеркала был сведён к интегрированию обыкновенного дифференциального уравнения, разрешённого относительно производной [15].

В настоящей работе авторы используют аналогичный подход для расчёта преломляющего оптического элемента, фокусирующего пучок с плоским волновым фронтом в кривую заданной формы. Для преломляющей поверхности оптического элемента получено аналитическое выражение, соответствующее огибающей семейства гиперболоидов вращения, каждый из которых фокусирует падающий пучок в точку на линии. Расчёт параметров гипербо- лоидов вращения, обеспечивающих формирование вдоль кривой фокусировки заданного распределения энергии, в приближении тонкого оптического элемента сведён к решению дифференциального уравнения первого порядка, разрешённого относительно производной. В качестве примеров рассчитаны оптические элементы для фокусировки в отрезок и в кривую, состоящую из двух дуг окружности. В работе также продемонстрировано применение предложенного метода для фокусировки плоского светового пучка в дискретный набор точек на кривой.

1.    Расчёт преломляющей поверхности для фокусировки в кривую

Рассмотрим задачу расчёта преломляющего оптического элемента (показатель преломления материала элемента – n ) для фокусировки пучка с плоским волновым фронтом в заданную линию (рис. 1). Направление падающего пучка совпадает с осью Oz . Оптический элемент ограничен двумя поверхностями (рис. 1). Первая поверхность элемента является плоской и лежит в плоскости z =0. Вторая поверхность является поверхностью свободной формы и описывается функцией z = H ( x ), где x = ( x , y ) e D – декартовы координаты в плоскости z =0, D – апертура элемента. Задача состоит в расчёте функции H ( x ) , обеспечивающей фокусировку падающего пучка в кривую, расположенную в плоскости z = f и заданную в параметрическом виде:

X ф = ( X ф, Y ф, f ), (1)

где ^ e [0, d ] - натуральный параметр. При этом вдоль кривой должно быть сформировано заданное распределение энергии, описываемое функцией I ( ^ ) , ^e [ 0, d ] .

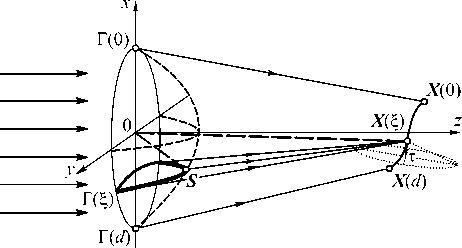
Рис. 1. Геометрия задачи фокусировки в линию

Сначала рассмотрим расчёт преломляющей линзы, фокусирующей плоскую волну (с направлением p = (0,0,1)) в некоторую точку линии. Первую поверхность линзы будем считать плоской, расположенной в плоскости z = 0. Для второй поверхности h ( x ) из принципа Ферма несложно получить следующее неявное уравнение:

n ■ h ( x , y ) + | X© - S| = v©, (2)

где S = ( x , y , h ( x , y ) ) - радиус-вектор точки на поверхности оптического элемента, у© — константа. При условии (2) оптическая длина путей лучей от исходного плоского волнового фронта (от плоскости z = 0) до точки X ( £ ) есть величина постоянная. Уравнение (2) записано в предположении, что показатель преломления среды вне линзы n ₀ = 1. Константа у© в (2) соответствует эйконалу светового поля в точке фокусировки X ( £ ) .

Известно, что преломляющая поверхность, фокусирующая в точку сферический световой пучок от точечного источника, является картезианским овалом [7, 16]. Таким образом, при фокусировке плоского пучка в точку преломляющая поверхность является частным случаем картезианского овала, когда один из фокусов (источник света) расположен в бесконечности. В этом случае картезианский овал соответствует гиперболоиду или эллипсоиду вращения (в зависимости от показателей преломления сред, разделяемых поверхностью). При условии n / n ₀ >  1 поверхность (2) является гиперболоидом вращения.

Поверхность для фокусировки в линию (1) является огибающей семейства гиперболоидов вращения (2) по параметру ξ. Действительно, по определению огибающая поверхность касается каждого из гиперболоидов семейства (2) вдоль некоторой кривой. Поскольку направления нормалей огибающей поверхности и гиперболоидов (2) вдоль кривых касания совпадают, то преломлённые лучи будут сфокусированы в точки на кривой (1). Таким образом, расчёт преломляющей поверхности для фокусировки в линию (1) сводится к построению огибающей для семейства гиперболоидов вращения (2) по параметру ξ.

Огибающая поверхность определяется уравнением (2) и его производной по параметру ξ [17]:

( X© - S d X ( ^ ) L d y ( ^ ) _v |X ( ^ ) - S| ’ d ^ J      d ^

Уравнение (3) является уравнением кругового конуса с вершиной в точке кривой X ( £ ) и осью

Т = d X® d ^

, совпадающей с касательной к линии (1)

(рис. 1). Так как ξ является натуральным парамет- ром, то |т| = 1, а производная эйконала dy(^) d^

опре-

деляет косинус половинного угла при вершине конуса. Таким образом, огибающая поверхность состоит из набора кривых Г©, £ e [0, d ], являющихся пересечением конусов (3) с гиперболоидами вращения (2). При этом лучи, приходящие с кривой Γ(ξ) в точку кривой X (ξ), лежат на поверхности конуса (3).

Уравнения (2), (3) определяют уравнение поверхности оптического элемента в неявном виде в декартовых координатах.

2.    Расчёт поверхности оптического элемента в криволинейных координатах

Поверхность оптического элемента для фокусировки в кривую может быть записана в простом аналитическом виде при использовании специальных криволинейных координат, связанных с лучами. Введём для линии (1) вектора касательной, нормали и бинормали:

• *® = ( ^ ,d Y ( S ) ,0 1

( d 5     d 5    J

чёта функции v ( 5 ) будем использовать закон сохранения светового потока. Для записи закона сохранения светового потока введём проекции Г_± ( 5 ) кривых Γ(ξ) на плоскость z = 0. Согласно (6), (7), проекции Г_± ( 5 ) имеют вид:

x ( 5 , ф ) = X © + ( nf -v ( 5 ) )х

d X © dv© - d Y© d 5 d 5      d 5

у

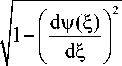
х

n ( 5 ) =1-

d Y ( 5 ) d X© d 5 ’ d 5

,0 I ,

n 1

^^^^^^в

dv© d 5

cos (ф)- 1

I ^{sin (}ф)

,

У © ф) = Y © ⁺ ( nf ^- v© ) ^х

b = ( 0,0, - 1 ) .

х

d Y ©dv© d X ( 5 ) d 5    d 5 ⁺ d 5

у

n 1

^^^^^^в

dv© d 5

^^^^^^в

f dv©) ■ / А [^^J ^{sin (}ф)

cos (ф)- 1

У

.

Уравнения (8) связывают декартовы координаты ( x , y ) с криволинейными координатами (ξ, φ). Ко-

Единичный вектор образующей конуса (3) но представить в системе координат (4) в виде:

p ( 5 , ф ) = t ( 5 )cos (a) + n ( 5 )sin (a) sin (ф) +

+ b sin (a) cos (ф) ,

мож-

где a = arccos

| d y ( ^ ) |

I d 5 ^J

– половинный угол при вер-

ордината 5 в (8) определяет кривую Г_± ( 5 ), а координата ф - положение точки на этой кривой.

Световой поток, заключённый между кривыми

Г_± ( 5 ) и Г_± ( 5 + А£ ), записывается в виде:

ф 2 ( 5 )

_Л .     . „ г' _г /„ х _т I „ dv d²v I .

АФ = А5 1 0 (5,ф) J ©,ф©г;:хг I dф, d5 d5 J

ф 1 (У

где I 0 (ξ, φ) – распределение освещённости падающе-

го светового пучка,

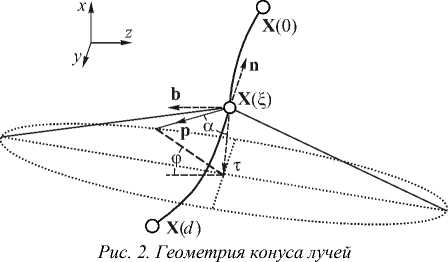
шине конуса, φ – угол в основании конуса, отсчитываемый от вектора b по направлению к вектору n© (рис. 2). С использованием криволинейных координат ( 5 , ф ) уравнение поверхности оптического элемента может быть представлено в виде:

S(^, ф) = ( x (5, ф), у © ф), z © ф) ) = = X(^) + p(^, ф) ■ l © ф), где l© ф) - расстояние вдоль вектора луча от точки поверхности до точки на кривой (1) (рис. 1). Подставив (6) в (2), получим:

l © ф) =

nf -v ( 5 ) ⁿP_z © ф) ⁺ 1.

Уравнения (6), (7) определяют поверхность оптического элемента в аналитическом виде и зависят от функции эйконала v ( 5 ). Эта функция определяет распределение энергии вдоль линии фокусировки (1). Рассмотрим расчёт v ( 5 ) из условия формирования заданного распределения энергии I (5) , 5 е [ 0, d ] вдоль кривой фокусировки. Для рас

.^f          d v d ²v

J I ⁵ ф ; v ^{( 5 )};    ;

у          d 5 d 5

du(5, ф) dv(5, ф) du (5, ф) dv(5, ф) ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B  ^^^^^^B  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B d5 дф дф д5

якобиан преобразования координат (8). Согласно (8), якобиан (10) зависит от функции эйконала v(5), а также от её первой и второй производных. Пределы интегрирования φ1(ξ) и φ2(ξ) в (9) определяют точки пересечения кривых Г± (5) с границами апертуры в плоскости z = 0. Например, для круговой апертуры с радиусом R функции φ1(ξ) и φ2(ξ) находятся из уравнения x2 (5, ф) + У2 (5, ф) = R2. (11)

Согласно построению оптического элемента световой поток ∆Φ, заключённый между кривыми Г_± ( 5 ), Г_± ( 5 + А5 ), переходит в сегмент кривой длиной А^, ограниченной точками X ( 5 ) и X ( 5 + А5 ). Соответственно, световой поток на единицу длины кривой фокусировки можно записать в следующем виде:

ДФ

I ( С ) = lim = д . дс

Ф 2 (^С)                 (

d v d V |

= I I о (^С v ) J i^v ; ^ ( ^С »;₁₁;,,. I ^d Ф .

^J             ।            dC d ^ J

п2(С)              I

I (С)= j Iо (С, n)J I С, п; а (С);— I dn •(16)

т(С))           V

Ф 1 (^С)

Функция I ( с ) в (12) определяет линейную плотность энергии вдоль кривой. При заданной линейной плотности I ( с ) уравнение (12) становится нелинейным дифференциальным уравнением второго порядка относительно функции v ( O • Таким образом, расчёт оптического элемента для фокусировки в линию сводится к решению уравнения (12) относительно функции v ( O и последующему расчёту поверхности по аналитическим выражениям (6), (7).

Функцию а ( С ) можно получить из (16) из условия формирования заданной линейной плотности энергии I ( С ) . Действительно, подставляя (15) в (16), получим для функции а ( С ) следующее дифферен-

циальное уравнение:

d q ( С ) = d C =

П 2 ^(С)

I ( С ) - ( а ² ( С ) + 1 ) K ( С ) j I о ( С , n ) n d n

П 1 ( С )

П 2 (^С)                    'I /П 2 (^С)                  ______________

^- j I 0 (^{c ,} n ) d n      j I 0 (^{c ,} n )V f ² +n ² d n .

П 1 ( С )                                 П 1 ( С )

3. Закон сохранения светового потока в приближении тонкого оптического элемента

Решение нелинейного дифференциального уравнения (12) является сложной вычислительной задачей. Его можно существенно упростить в приближении тонкого оптического элемента. В этом случае в качестве проекций Г_± ( С ) можно приближённо

В отличие от уравнения (12), интегрирование уравнения (17) является тривиальной вычислительной задачей и может быть выполнено с помощью

стандартных численных методов, например метода Рунге–Кутты.

Выражения для преломляющей поверхности (6), (7) зависят от функции эйконала и её производной, которые несложно получить из (14) в виде:

рассматривать кривые, которые являются пересечением конусов (3) с плоскостью z =0. Указанные кривые являются гиперболами и могут быть получены из уравнений (5), (6) в виде [18, 19]:

, ( С , п ) = X ( С ) + а ( С ) 7 f ’ +П ^-П ^,

^{С С} (13)

y (с,n) = Y(С)+а (С) Х7 dYjC^i+n‘Xy, где а (С) = 5>V®/ 1 dC    У

^d CC ) J ^, п = f tg ( ф ) •   ⁽¹⁴⁾

п                   dv(O

Поскольку производная —dc— соответствует косинусу половинного угла при вершине конуса лучей (3), то функция а ( С ) в (14) соответствует котангенсу половинного угла при вершине конуса.

Якобиан преобразования координат (13) имеет вид:

Ie

J \ ^{c ,} п ; а ^{( С )};— 1 =

I

= ^{1 +} dadr     "  Р a ² "^{1 )} K ^(С) ,

где K ( С ) =

d2X(С) dY(С) dX(С) d2Y(С) dC2    dC      dC

– кривиз-

на линии (1). Якобиан (15) зависит от функции а ( С ) и её первой производной.

В приближении тонкого оптического элемента закон сохранения светового потока (12) принимает вид:

dV^L ^* « )₌, v ( 5 ) = J -,O(tL₌ d t.   (18)

^{d C}      V1 + а ²( С )           ^j V1 + а ²( t )

Таким образом, выражения (6), (7) (17) и (18) представляют собой законченное решение задачи фокусировки в кривую (1) с заданным распределением линейной плотности энергии I (ξ). При этом расчёт поверхности оптического элемента состоит из следующих шагов:

• 1)    Выбор вида кривой фокусировки (1), требуемого распределения линейной плотности энергии и распределения освещённости падающего пучка.

• 2)    Численное интегрирование дифференциального уравнения первого порядка (17).

• 3)    Расчёт функции эйконала и его производной по формулам (18).

• 4)    Расчёт поверхности оптического элемента по формулам (6), (7).

4.    Фокусировка в отрезок и в составную из двух дуг окружности кривую

Таким образом, расчёт поверхности оптического элемента сводится к решению обыкновенного дифференциального уравнения первого порядка, разрешённого относительно производной, (17) и последующему интегрированию полученного решения в (18).

Отметим, что полученное решение является приближённым, поскольку расчёт функции ^ ( С ) , определяющей распределение линейной плотности энергии вдоль линии фокусировки, выполнен в приближении тонкого оптического элемента. Тем не менее результаты расчёта, представленные в следующем пункте, показывают возможность использования данного приближения даже при расчёте оптических элементов с большой числовой апертурой (когда углы преломлённых лучей с осью Oz достигают 28°).

Для демонстрации работоспособности разработанного метода были рассчитаны оптические элементы с круглой апертурой для фокусировки свето- вого пучка с равномерным распределением освещённости 10 (x) = 10 в отрезок и в кривую, состоящую из двух дуг окружности. Для обеих кривых была задана постоянная линейная плотность энергии I (^) = I, ^ е [0, d]. Параметрические урав- нения указанных кривых имеют вид:

Xarc (^) = Rarc *

7- Sin ( ( ^ ^- d /2 ) / R arc ) ,    )

cos ( ( §- d /2 ) / R are ) + 1, , ^Е 0, d ,

*5

f / R are

k

' sin №^{- d /2} ) / ^R arc ) ’ cos ( ( ^- d /2 ) / R are ) - 1,

J arc

_e d j

’ ^ ^£ 2’ d ’

а)

Рис. 3. Преломляющие оптические элементы

где Rarc - радиус дуг окружностей, а фarc = R arc

/ d –

угловой размер дуг. Расчёт производился по формулам (6), (7), (17), (18) при следующих параметрах: радиус апертуры R =20 мм, расстояние до плоскости фокусировки f =50 мм, длина отрезка d = 10 мм, радиус дуг окружностей Rarc =5,7 мм, угловой размер дуг Фarc = 45°.

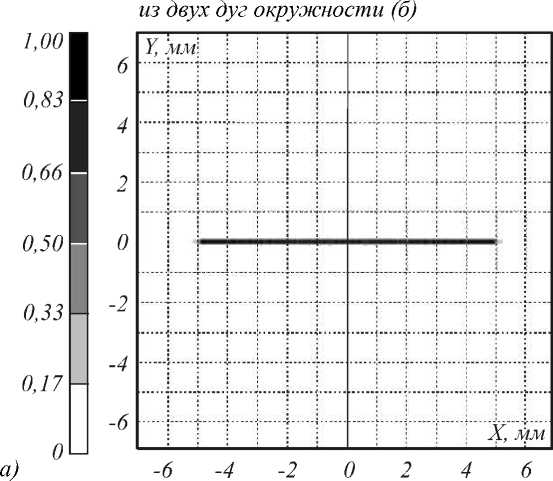
Рассчитанные элементы приведены на рис. 3. Излом поверхности с рис. 3 б в центральном сечении (в плоскости x = 0) объясняется тем, что вектор кривизны линии (20) в точке X (0) меняет знак. Расчётные распределения освещённости, формируемые элементами с рис. 3, приведены на рис. 4. Распределения освещённости на рис. 4 были рассчитаны с использованием коммерческой программы по светотехнике TracePro [20] при коллимированном падающем пучке с постоянной освещённостью. Результаты моделирования показывают высокое качество фокусировки в заданные кривые. Несмотря на то, что использованное при расчёте уравнение (17) является приближённым, рассчитанные распределения освещённости вдоль линий близки к равномерным распределениям (среднеквадратические отклонения полученных распределений от равномерного составляют менее 5%). Отметим, что при указанных параметрах углы преломлённых лучей с осью Oz достигают 28°, то есть рассматриваемые оптические элементы работают в существенно непараксиальном режиме.

б)

для фокусировки в отрезок (а) и в кривую, состоящую

б)

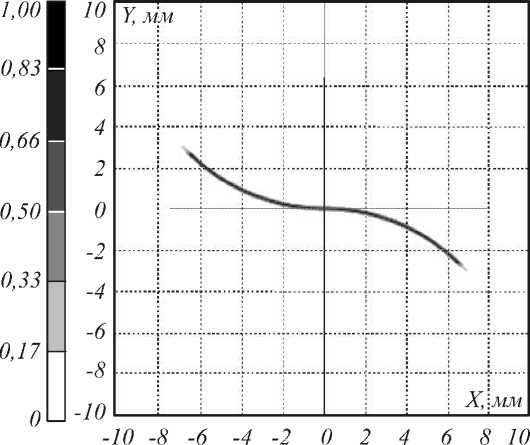
Рис. 4. Распределения освещённости, формируемые рассчитанными оптическими элементами для фокусировки в отрезок (а) и в кривую, состоящую из двух дуг окружности (б)

5.    Фокусировка в набор точек на кривой

В работах [6–8] рассмотрены итерационные методы для решения обратной задачи фокусировки в набор точек. Предложенный в данной работе метод позволяет получить аналитическое решение задачи расчёта преломляющей поверхности для фокусировки в набор точек, лежащих на кривой (1). В этом случае поверхность представляет собой набор сегментов линз, каждый из которых фокусирует падающий на него световой пучок в соответствующую точку.

Набор точек на кривой (1) определим в виде:

Xp (I) = X(I,), £g[I,^), г = 1,^+1,     (21)

где ¹ =

I+I + .

– центральная точка полуинтервала

[ I . I + . ) . I = N ( , - 1 ) . N -

количество точек, в ко-

торые производится фокусировка.

Расчёт поверхности оптического элемента для фокусировки в набор точек (21) производится по ранее полученным формулам (5), (6), (7), (17) (18). Отличие от случая фокусировки в кривую (1) состоит в том, что в выражении (7) вместо непрерывной функции эйконала у ( I ) используется кусочно

Рис. 5. Преломляющие оптические элементы для фокусировки в набор точек на отрезке (а)

постоянная функция у p ( I ):

v p ( I ) = v ( l ) , Ie [ l , I + 1 ) , , = 1, N Ti.      (22)

Рассчитанные описанным выше способом оптические элементы для фокусировки в набор точек на отрезке и в набор точек на кривой из двух дуг окружности представлены на рис. 5. На рис. 6 представлены результаты моделирования распределений освещённости, формируемых рассчитанными оптическими элементами, в программе TracePro. Они показывают высокое качество фокусировки в заданный набор точек.

Заключение

Предложено аналитическое представление преломляющей поверхности для фокусировки в заданную кривую в виде огибающей семейства гиперболоидов вращения. В приближении тонкого оптического элемента задача фокусировки в кривую с заданным распределением линейной плотности энергии сведена к решению обыкновенного дифференциального уравнения первого порядка, разрешённого относительно производной. Результаты моделирования распределений освещённости, формируемых элементами, рассчитанными из условия фокусировки в отрезок и дугу окружности, показывают эффективность предложенного метода. Предложено применение разработанного метода для фокусировки в дискретный набор точек на кривой. Рассчитаны оптические элементы для фокусировки в набор точек на отрезке и на кривой, состоящей из двух дуг окружности. Результаты моделирования работы рассчитанных элементов показывают эффективность предложенного метода.

б)

а)

0,17

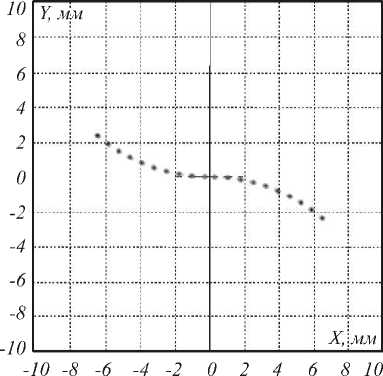
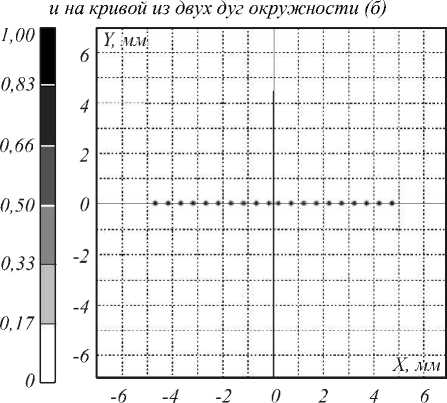
Рис. 6. Распределения освещённости, формируемые рассчитанными оптическими элементами для фокусировки в наборы точек на отрезке (а) и на кривой, состоящей из двух дуг окружности (б)

Представленный метод может быть обобщён на случай освещающего пучка с произвольным волновым фронтом. В этом случае поверхность оптического элемента представляется в виде огибающей семейства поверхностей, фокусирующих падающий пучок в точки линии. В частности, при сферическом освещающем пучке поверхность оптического элемента представляется в виде огибающей семейства картезианских овалов.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации и грантов РФФИ 12-07-31055, 12-07-31193, 12-07-13113, 13-07-97001.