Аналитический вариант решения задачи о вероятности одновременного возникновения событий техногенного характера, инициирующих пожары и взрывы

For definition of likelihood characteristics of failures, fires, explosions frequently it is necessary to define probability of simultaneous occurrence of 2 and more independent events (for example, occurrences of the combustible environment and an ignition source). Thus for definition of probability of simultaneous occurrence of independent events within a year in some techniques the formula of multiplication of probabilities is used. In article the doubt in adequacy of such principle as it, according to the author, overestimates total probability in comparison with results of stochastic modeling is stated. Other analytical dependence Is offered ^∗ .

^∗ Sedov D.V. Analytical variant of the decision of the problem about probability of simultaneous occurrence of events of the technogenic character initiating fires and explosions.

Постановка проблемы

При определении вероятностных характеристик техногенных аварий, пожаров, взрывов возникает необходимость нахождения вероятности одновременного возникновения, по крайней мере, двух независимых событий в течение периода наблюдения. Например, аварийный выход жидкости из резервуара в окружающую среду произойдет в течение года, если в течение года совпадут период заполнения резервуара и период отказа датчика уровня. Пожар в течение года произойдет, если одновременно возникнет утечка горючей жидкости из емкости и короткое замыкание электропроводки с образованием искр. Взрыв в течение года произойдет, если в период образования взрывоопасного облака около резервуара в него ударит молния.

Согласно подходу, принятому в некоторых нормативных документах и некоторых литературных источниках, для определения вероятности одновременного возникновения событий А и Б предписывается перемножать их вероятности:

Q В = Q А Q Б , (1)

где Q В - вероятность одновременного возникновения событий А и Б в течение периода наблюдения; Q _А и Q Б - вероятности возникновения событий А и Б в течение периода наблюдения.

Так, [1, формула 40] для определения вероятности образования к -й горючей среды для случая независимости событий ГВ (появление горючего вещества) и ОК (появление окислителя) указывается выражение: Q i (ГС к ) = Q i (ГВ i ) Q i (ОК m ), где Q_; (ГВ i ) - вероятность появления достаточного для образования горючей среды количества l -го горючего вещества в i -м элементе объекта в течение года; Q i (ОК m ) - вероятность появления достаточного для образования горючей среды количества m -го окислителя в i -м элементе объекта в течение года; к , l , m - порядковые номера горючей среды, горючего вещества и окислителя.

В том же документе [см. формула 45] для вероятности подсоса окислителя в аппарат с горючим веществом (событие b ₂ ) закреплена формула: Q i (b ₂ ) = Q i (S i ) Q i (S ₂ ), где Q i (S i ) - вероятность нахождения i -го элемента объекта под разрежением; Q i (S ₂ ) - вероятность разгерметизации аппарата.

По аналогичному принципу в [1] определяются вероятность появления в i -м элементе объекта искр короткого замыкания [формула 55], вероятность появления i -м элементе объекта искр статического электричества [формула 57].

В [2] приводится пример «дерева отказа» и дается пояснение: «Для связи между событиями в узлах “деревьев” используются знаки “И” и “ИЛИ”. Логический знак “И” означает, что вышестоящее событие возникает при одновременном наступлении нижестоящих событий (соответствует перемножению их вероятностей для оценки вероятности вышестоящего события)».

В [3] при комментировании «дерева неисправностей» указывается: «Операция “И” означает, что перед тем, как произойдет некоторое событие

“А”, должно произойти несколько событий, например, “Б” и “В”. В вероятностном аспекте такая операция выражается логическим произведением: Р (А) = Р (Б)* Р (В)».

На наш взгляд, простое перемножение вероятностей искажает реальную картину, потому что позволяет определить лишь вероятность того, что все рассматриваемые события произойдут в течение периода наблюдения и не более. Но это еще не гарантирует того, что события произойдут одновременно. Например, загорание в помещении в течение года не произойдет, даже если горючая среда и источник зажигания возникнут в течение года, но не будут сосуществовать в один и тот же момент, не будут «пересекаться»1.

Перемножение вероятностей не учитывает фактор, который оказывает главное влияние на возможность возникновения «пересечения», – длительность существования событий. Пожалуй, большинство реальных случайных физических явлений, событий, процессов имеют определенную длительность, т.е. период, в течение которого они существуют после своего возникновения. Длящимся событием является, например, аварийная утечка горючего газа через фланцевое соединение: она возникает случайно и длится в течение времени до устранения аварии. Другой пример – поступление паров бензина в окружающее пространство с поверхности разлива, образовавшегося при обрыве сливного рукава автоцистерны. Данное событие является случайным и длится до момента покрытия поверхности разлива пеной.

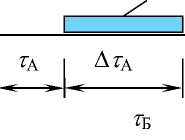
Для иллюстрации одновременного возникновения длящихся событий рассмотрим следующую модель. В течение года может произойти событие А и событие Б. Время τ _А до возникновения события А и время τ _Б до возникновения события Б являются случайными величинами. Событие А после возникновения длится в течение Δ τ А , событие Б – Δ τ Б . Если событие А и событие Б будут сосуществовать в одни и те же моменты времени, образующие некоторый интервал «пересечения», то произойдет опасное событие В.

На рис. 1 а показан случай, когда и событие А, и событие Б происходят в течение периода наблюдения τ. Вероятность их появления в течение τ определяется по формуле (1), но, как видно из рис. 1 а, «пересечения» не наблюдается. Действительно, события А и Б могут возникнуть один за другим с отставанием, допустим, в 1 мин. Но если каждое из данных событий длится несколько секунд, то даже такое близкое по времени возникновение не приведет к их «пересечению», т.е.

появлению опасного события В (рис. 1 б ).

Событие А

Событие Б

Δ τ Б

т

Время

а)

Событие А    Событие Б

Событие В

Время

б)

Рис. 1. Интерпретация одновременного возникновения («пересечения») двух независимых событий с ненулевой длительностью в течение периода наблюдения: а - «пересечение» событий не происходит, хотя оба события возникают в течение одного и того же периода наблюдения т, б - «пересечение» событий в течение периода наблюдения т происходит

По-видимому, вероятность показанного на рис. 1 б «пересечения» должна быть значительно меньше, чем вероятность, получаемая по формуле (1). Ведь для возникновения «пересечения» еще недостаточно, чтобы события А и Б произошли в рамках периода наблюдения. Необходимо, чтобы они какое-то время происходили одновременно, «пересекались». Впрочем, вероятность «пересечения» двух событий в течение периода наблюдения может оказаться и равной произведению их вероятностей, но только в том случае, если длительность каждого события ( Л т _А и Л т _Б ) будет равна или превышать период наблюдения ( τ ). В этом частном случае (о нем будет сказано ниже) для возникновения «пересечения» действительно достаточно, чтобы события А и Б произошли в течение рассматриваемого интервала времени.

Таким образом, одновременное возникновение событий А и Б в течение какого-либо периода не гарантирует «пересечения» данных событий. «Пересечение» (событие В) может произойти лишь в одном из двух случаев: 1) первым в течение периода наблюдения возникает событие А, а событие Б возникает в то время, пока событие А еще длится; 2) в течение периода наблюдения первым возникает событие Б, и пока оно длится, возникает событие А. Если события А и Б возникают в один и тот же момент времени, то «пересечение» происходит, хотя данный случай является математически невозможным, ведь «момент времени» имеет бесконечно малую длительность.

Стохастическое моделирование «пересечения» двух случайных независимых длящихся событий

С целью получения идеализированной картины исследуемого процесса, когда рассматриваемые события строго подчиняются экспоненциальному закону распределения вероятностей, нами было проведено стохастическое моделирование возникновения «пересечений». Полученные результаты о вероятности «пересечения» двух случайных событий А и Б использовались для построения эмпирической функции распределения времени до момента «пересечения». Данная эмпирическая функция распределения в дальнейшем рассматривалась в качестве ориентира при выводе аналитического выражения для теоретической функции распределения. При стохастическом моделировании использовался генератор равномерно распределенных случайных чисел программы Microsoft Office Excel 2007.

В качестве случайных величин рассматривались периоды Т А и Т Б до возникновения А и Б. Было принято, что интенсивности появления событий не зависят от времени, т.е. закон распределения А и Б является экспоненциальным. Для получения случайных экспоненциально распределенных величин использовалось выражение:

E = - ln(1 - R) , где E – экспоненциально распределенное случайное число; R – равномерно распределенное случайное число от 0 до 1. Случайная величина Е принимает любые значения в интервале от 0 (при R = 0) до ∞ (при R = 1). Значения времени до возникновения событий А и Б определялись по формулам:

г А = Т А E = - Т А ln ( 1 - R ) = - ^ln ( 1 - R ) ,

^А гБ = ТБE = -ТБ ln(1 - R) = -^ln(1 - R),

^Б где ТА и ТБ – средние периоды времени до возникновения событий А и Б соответственно; λА и λБ – интенсивности возникновения событий А и Б соответственно.

Средние периоды времени до возникновения событий Т А и Т Б , длительности событий А г А и А т _б , а также размер периода наблюдения т задавались как исходные данные.

Факт возникновения «пересечения» событий А и Б в течение периода наблюдения г, определялся путем сопоставления момента возникновения первого события с моментом возникновения второго события. Сопоставление проводилось в соответствии с блок-схемой, представленной на рис. 2.

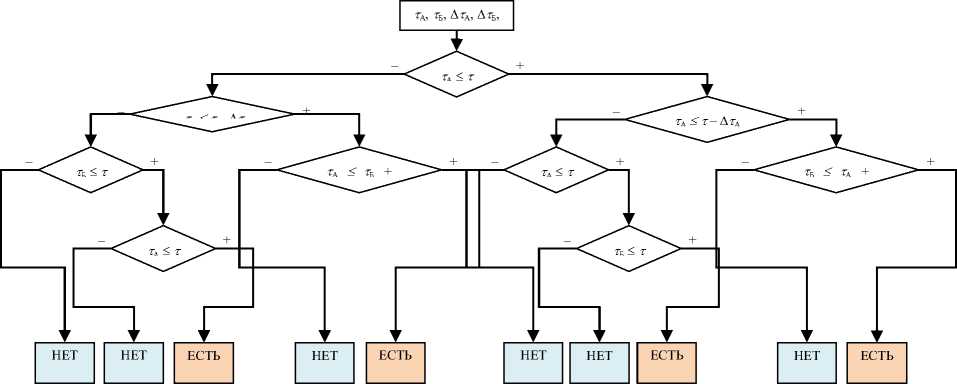
Рис. 2. Блок-схема для фиксации «пересечений» независимых случайных длящихся событий А и Б в процессе стохастического моделирования их возникновения

Согласно блок-схеме на рис. 2 между собой сравниваются периоды Т А и т _б . Если т А <  т б, значит событие А происходит одновременно или раньше, чем событие Б. Если при этом событие А успевает просуществовать в рамках периода наблюдения τ в течение всей своей длительности Δ τ _А , то для возникновения «пересечения» необходимо, чтобы событие Б произошло в течение интервала от 0 до τ А + Δτ А , т.е. в период, пока событие А еще длится. Если событие А возникает внутри рассматриваемого периода τ , но не успевает полностью просуществовать, то для «пересечения» необходимо, чтобы событие Б произошло в интервале от Т А до т . Если же первым возникает событие Б, то анализ стохастических данных производится по аналогичной схеме, в которой индексы А и Б меняются друг с другом. Таким образом, всего существует четыре варианта «пересечения»: два варианта, когда первым возникает событие А, и два, когда первым появляется Б.

Все зафиксированные в течение т «пересечения» подсчитывались. Их количество N₀( t ) при известном общем числе испытаний N позволило определить эмпирическую вероятность q_b ( т ) «пересечения» в течение периода наблюдения:

Q (т ) = ^^-

Так, было принято, что событие А длится в течение Ата = 10 ч, событие Б - в течение Атб = 2 ч. Средние периоды до возникновения событий ТА = 104 ч и ТБ = 2-104 ч (ЛА = 1/ТА = 10-4 ч-1; ЛБ = 1/ТБ = 5^10"5 ч-1). Расчетный период времени, в пределах которого наблюдались «пересечения», т = 1 год.

В результате 1 млн статистических испытаний (1 млн однолетних стохастических численных «экспериментов») получено 293 «пересечения», т.е. в среднем эмпирическая вероятность «пересечения» в течение года составила о! = 2,93 - 10^-4.

B

По формуле (1) получился следующий результат: Q b ( т ) = Q a ( т Q (т ) = ( 1 — e - ^Л А ^т )( 1 — e - ^Л ' ^т ) = 0,207.

Данная величина почти в 700 раз больше полученной при моделировании, т.е. отличается от вероятности «пересечения» идеализированных событий.

Было проведено стохастическое моделирование для различных периодов наблюдения, длительностей и средних времен до возникновения событий. Полученные значения эмпирической функции распределения представлены в виде графиков на рис. 3 и 4.

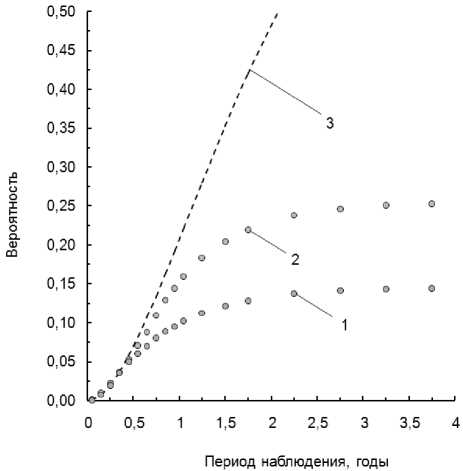
Рис. 3. Вероятность «пересечения» двух независимых случайных длящихся событий при изменении их длительности ( Т А = 1,14, Т Б = 2,28 года):

1 - эмпирическая функция распределения времени до момента «пересечения» для Д т _А = 0,3 года, Д т Б = 0,25 года;

2 - то же для Д т _А = 0,75 года, Д т Б = 0,25 года;

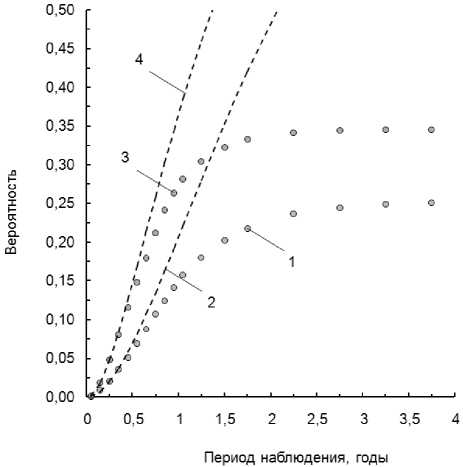
Рис. 4. Вероятность «пересечения» двух независимых случайных длящихся событий при изменении среднего времени до их возникновения ( Д т а = 0,75, Д т б = 0,25 года):

1 - эмпирическая функция распределения времени до момента «пересечения» для Т _А = 1,14, Т Б = 2,28 года;

2 - результаты расчета по формуле (1) для Т А = 1,14, Т Б = 2,28 года;

3 – результаты расчета по формуле (1)   3 – эмпирическая функция распределения для ТА = 0,57, ТБ = 1,71 года;

4 – результаты расчета по формуле (1) для Т А = 0,57, Т Б = 1,71 года

Из рис. 3 и 4 видно, что при малых значениях времени эмпирическая функция распределения увеличивается медленно, после чего темпы ее роста увеличиваются, и на значительном удалении от нуля рост функции замедляется. При периодах наблюдения, значительно превышающих Т _А и Т _Б , рост функции практически останавливается. Это объясняется тем, что события А и Б в основном происходят в окрестности Т А и Т Б и практически не возникают на значительном удалении от них, а значит, и вероятность «пересечения» при очень больших периодах наблюдения оказывается такой же, как и при малых.

Видно также, насколько разные значения принимает зависимость, полученная при стохастическом моделировании, и формула (1). Заметим все же, что при малых значениях τ рассматриваемые графики совпадают. Это объясняется тем, что на данном участке периоды наблюдения оказываются меньше длительностей Δ τ A и Δ τ Б , и для «пересечения» становится достаточным, чтобы А и Б лишь возникли в течение τ , т.е. при малых значениях времени формула (1) становится справедливой. Таким образом, формула (1) не в полной мере корректно описывает процесс возникновения «пересечения».

Как видно из рис. 3, при уменьшении длительности событий Δ τ A и Δ τ Б значения эмпирической функции распределения уменьшаются. График же, построенный по формуле (1), остается без изменений. При увеличении среднего времени до возникновения событий Т _A и Т _Б (уменьшении интенсивности) эмпирические значения увеличиваются (см. рис. 4). График, построенный по формуле (1), также меняется.

Вывод теоретической зависимости для вероятности «пересечения» двух случайных независимых длящихся событий

Общие замечания. Большое влияние на вероятность «пересечения» оказывают длительности событий. Если длительность события, которое возникает первым, меньше периода наблюдения τ, то второму событию необходимо возникнуть в те моменты, пока первое событие еще длится. Если же длительность первого события велика и превышает τ, то второму событию достаточно возникнуть между моментом возникновения первого события и границей периода наблюдения. Таким образом, длительности событий определяют сам принцип построения теоретического выражения для вероятности «пересечения».

Так как при рассмотрении «пересечения» двух событий первым возникает либо одно, либо второе из них, то полная вероятность «пересечения» будет определяться суммой:

^QB ^(т ) = ^Q B|AA ^{( t} ) + ^Q В|ББ ^{( т} )’ (²) где Q _В|_АБ ( Т ) и Q в|_БА ( Т ), соответственно вероятность «пересечения», когда первым возникает событие А, и вероятность «пересечения», когда первым возникает событие Б.

Принцип определения каждой из вероятностей Q _В|_АБ ( Т ) и Q _ВБ_А ( т ) определяется в зависимости от длительностей событий А и Б. На рис. 5 представлена структурная схема возникновения «пересечения» для случая, когда длительность первого события меньше периода наблюдения, на рис. 6 - когда она равна или превышает его.

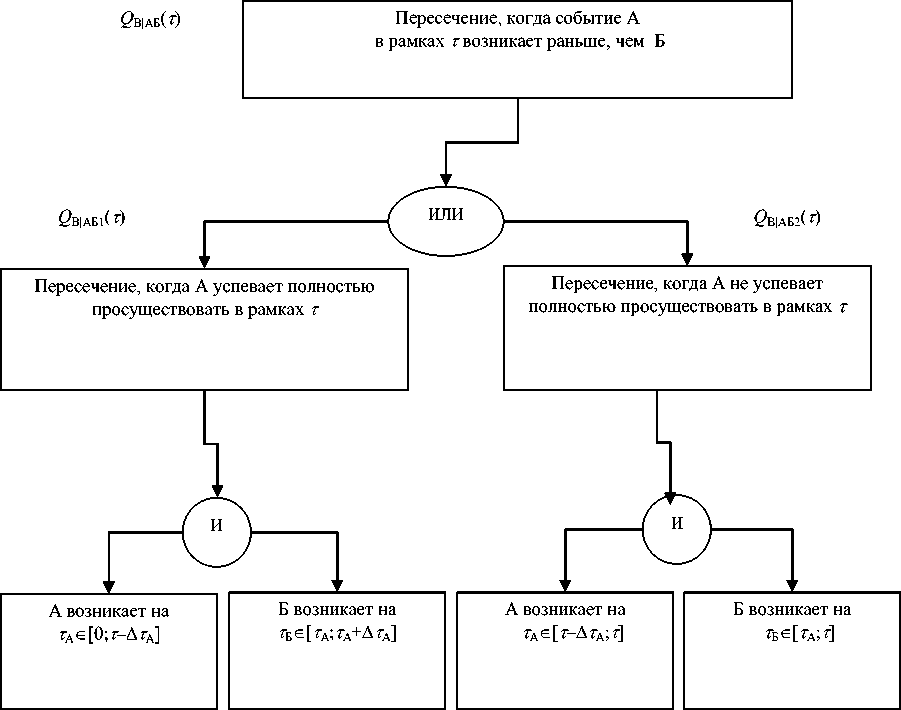
Рис. 5. Структурная схема возникновения «пересечения», когда длительность первого события (А) меньше периода наблюдения

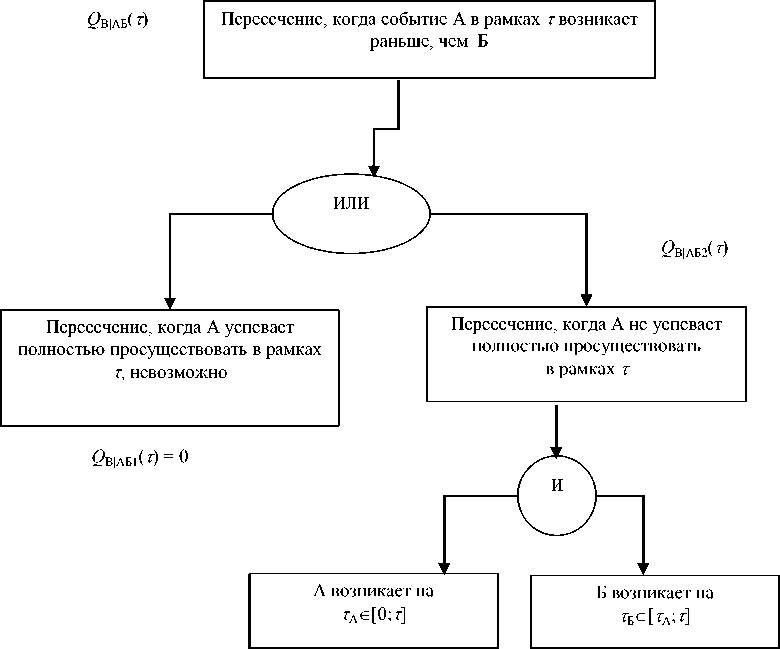
Рис. 6. Структурная схема возникновения «пересечения», когда длительность первого события (А) равна или превышает период наблюдения

Вероятность «пересечения», когда длительность первого события меньше периода наблюдения. Если длительность первого возникшего в рамках т события ( А т _а или А т Б ) меньше т , то данное событие может успеть в пределах т просуществовать в течение всей своей длительности, а может и не успеть. В этом случае и Q в|_АБ ( т ), и Q в|_БА ( т ) будут определяться в соответствии со схемой на рис. 5.

Выражение (2) для полной вероятности «пересечения» примет вид:

^Q B ^{( т} ) = ^Q В|ААБ ^{( т} ) + ^Q В|ААБ ^{( т} ) + ^Q В|ББА ^{( т} ) + ^Q В|ББА ^{( т} ) ^-(³⁾

Вероятность QВ|АБ1(т) можно найти как произведение вероятности того, что событие А, возникнув раньше Б, успеет просуществовать в течение Ата за наблюдаемый период т, и условной вероятности того, что событие Б, возникнув после А, произойдет в период, пока А еще длится:

Qbiaаб(т) = (1 — e-'А(т-Ата))(e-ХБтА - e-^Б(тА +АтА)) =

(1 _ e ^— ^ А ^{( т —А т} А ) ) е ^— ^ Б ^т А

—

e ^_ Я б ^Ат а

)

Следует заметить, что величина e ^А Б ^{т А}

, входящая в данную формулу,

является случайной, так как содержит случайное число тА, возникновение которого ограничено интервалом тАе[0; т-АтА]. На данном интервале можно определить среднее значение e

,^{— А} Б ^т А

. Для этого учтем, что случайное

число тА принимает различные значения не с равной вероятностью, а подчиняясь

экспоненциальному

закону,

т.е.

через

равномерно

распределенное число R его можно выразить как г_А

= —— ln ( 1 - R ) . Если в

А а

такой форме его подставить в e

' ^Ат А

, то получим:

e ^{- А} Б ^{т А}

= ( 1 - R ) ^А Б 'А . На

границах интервала т _А е [0; т- А т А ] число R будет принимать значения: R ₁ =

0, R ₂ = 1 - e ^АА^{(т Ат А} ) . Тогда в среднем величина e

" ^АБ^т А

составит:

R 2

-

R 1

R 2

J ( 1 — R ) ^{А б/ А а} d R =

R 1

R 2

•

А а

Б

-

R 1

Аа +

А а

—

e

^{— ( А} А ^{+ А} Б ^{)( т —А т} А )

•

Аа +

—

e

^{— А} а ^{( т а А} а а )

.

Таким образом, получаем выражение для Q _В а _Б1 ( т ):

^Q В|ААБ ^{( т )} = ^{( 1}

-

e

^{— А} А ^{( т —А т} А

-

e

^-А Б ^Ат а

)•

А а

—

e

^{— ( А} А ^{+ А} Б ^{)( т —А т} А )

•

—

e

^{— А} А ^{( т —А т} А )

А а

•(1

-

e - ^ Б ^{Ат А} )( 1

-

e

^{—( А} А ^{+ А} Б ^{)( т —А т} А ) )

Что касается вероятности Q _ВА_Б2 ( т ), то

она представляет

собой

произведение вероятности возникновения события А на участке тае[т-

А т А ; т ] и вероятности возникновения события Б на участке т_Бе[т_А; т ]:

Q В| АБ2

(т) =(e

—

^А А ^{( т —А т} А )

-

e

,^{— А} А ^т

x e

—

^А Б ^т А

-

e

.^{— А} Б ^т

)=

= e

.^{— А} А ^т

( e ^A A ^{А т} а

—

1x e

—

^А Б ^т А

—

e

.^{— А} Б ^т

).

,^{— А} Б ^т А

Здесь среднее значение было найдено для случайной величины e на участке тАе[т-АтА;т]. Оно составило:

А а

e

—

Б

e

--

•

А а

+

e

—ААт

( e A A A ^ A

--

.

Поэтому выражение для Q _ВА_Б2 ( т ) приняло вид:

Q В|АБ2

^(т ) =

„ —Ат e ^А

( e^-A^ а _— 1

А а

e

,^— ( ^А А ^{+ А} Б ^)г

e ( ^А а ^{+ А} б ^{)А т} а

—

= e

,^{—( А} А ^{+ А} Б ^)г

А а

• ( e ( А + А ) А

-

•

„—Ат e ^А

e ^A A ^{А т} а _ 1 )

—

e ^А Б ^т

0+1

-

e ^A A ^{А т} а

.

Вероятности же QВ|БА1(т) и QВ|БА2(т)  определяются аналогичным образом с той лишь разницей, что вместо А рассматривается Б, и наоборот.

Вероятность «пересечения», когда длительность первого события равна или превышает период наблюдения. Если А т _а >  т и А т Б >  т , то события А или Б не успеют просуществовать в течение всей своей длительности, в какой бы момент периода т они не возникли. Поэтому вероятности Q _ВА_Б1 ( т ) и Q _В|_БА1 ( т ) будут равняться нулю (см. рис. 6), а выражение (2) для полной вероятности «пересечения» примет вид:

^Q В ( ^Т ) = ^Q В|АБ2 ( ^{Т ) + Q} В|БА2 ( ^Т ^                ⁽⁶⁾

Вероятность Q _В|_АБ2 ( т ) равна произведению вероятности того, что А произойдет в течение периода наблюдения, т.е. на интервале Т а € [0; т ], и вероятности того, что Б произойдет в течение т _Б е [ т _А ; т ]:

^ ваб2 ( т ) = ( 1 - e — ^Л А ^т )( e — ^А — e ^{- Л} Б ^т ) .

Среднее значение величины ^{e Л;т А}

на участке т А е [0; т ] составит:

Л А ----------- • —

ЛА + Л 1

—

—Лт e А

• [ 1 — e ^{— ( Л} А ^{+ Л б т} ] .

Поэтому выражение для Q _ВА_Б2 ( т ) примет вид:

С в „. ( т ) = ( 1 — e-^Л А ^т ]^ХА

• --------------------:-------

1 — e ^{— Л} А ^т

[ 1 — e ~(X ^{+ Л} Б ^т ] — e - ^Л Б ^т

J

Л А

ЛА + ЛБ

( 1 — e ^{— ( Л а + Л б т} ) + 1 — e ^{— Л} Б ^т

По аналогии получается выражение для Q _ВБ_А2 ( т ).

Полная вероятность «пересечения» по формуле (6) составит:

Q ( т ) =-- ^{Л а} --( 1 — e "^{( Л а + Л} Б ^т ) + 1 — e "^хБ ^т

^В       Л а + Л б

^Л^_ • ( 1 — e "^{( Л а + Л б т} ) + 1 — e "^ЛА^т =

Л а + Л б ^{V           7}

= ( 1 — e ^{— Л} А ^т )( 1 — e ^—Л Б ^т ) .

Как видно, полученное выражение идентично формуле (1), т.е. формула (1) представляет собой частный случай вероятности «пересечения», когда длительности событий А и Б настолько велики, что превышают период наблюдения, либо период наблюдения настолько мал, что длительности оказываются больше него.

Вероятность «пересечения», когда длительность одного из событий меньше периода наблюдения, а длительность другого равна или больше. Если Ат _A >  т , а Ат _Б <  т , то формула для полной вероятности «пересечения» будет иметь вид:

Q B ^{( т} )   ^Q B|АБ2 ( J ) + Q В|БА1 ^{( т} ) + Q В|БА2 ^{( т} )’ ⁽⁸⁾

где вероятность Q _В|_АБ2 ( T ) будет определяться по формуле (7), а вероятности Q _В|_БА1 ( т ) и Q _В|_БА2 ( т ) - по аналогии с формулами (4) и (5), соответственно.

Если же А т _а <  т , а А т _б >  т, то формула для Q_В(т) будет иметь вид:

^{Q ( т} ) = ^Q B|АБ1 ^{( т} ) + ^Q B|АБ2 ^{( т} ) + ^Q В|БА2 ^{( т} )’ ⁽⁹⁾

где Q В|АБ1 ( Т ) и Q в|аб2( т ) определяются по (4) и (5), а Q В|БА2 ( Т - по аналогии с (7).

Таким образом, в общем виде вероятность «пересечения» можно определять по формуле (3). В зависимости от величины длитель-ностей событий слагаемые данной формулы будут рассчитываться по соответствующим выражениям. В частности, если длительности превышают период наблюдения, вероятности Q _В|_АБ1 ( т ) и Q _ВБ_А1 ( т ) становятся равными нулю.

Сравнение результатов стохастического моделирования и результатов аналитического расчета

С помощью программы Microsoft Office Excel 2007 были проведены расчеты по определению вероятности «пересечения» Q_В(т) с помощью полученного аналитичес-кого выражения. Было принято, что длительность события А составляет Ат _а = 0,75 года, события Б - А т _б = 0,25 года. Среднее время до возникновения события А равно Т А = 1,14 года, события Б - Т Б = 2,28 года. По результатам расчетов был построен график изменения вероятности «пересечения» Q _В ( т ) в зависимости от величины периода наблюдения т, а также графики, отражающие изменение всех слагаемых формулы ^(3): Q В|АБ1 ^{( т )}, Q В|АБ2 ^{( т )}, Q В|БА1 ^{( т ) и} Q В|БА2 ^{( т )}-

Для проверки корректности вывода аналитического выражения (3) для вероятности «пересечения» было проведено сравнение значений, полученных с помощью выражения (3), значений эмпири-ческой функции распределения, а также значений, получаемых с помощью зависимости (1). Результаты данного сравнения представлены на рис. 7.

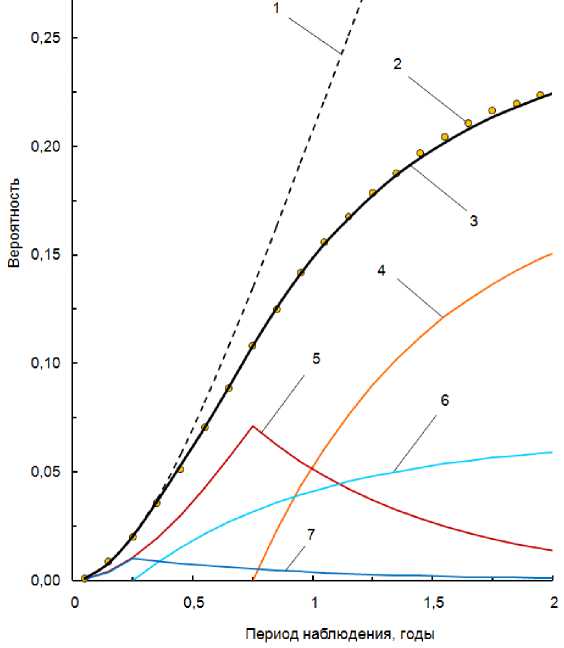
Рис. 7. Сравнение результатов стохастического моделирования и результатов аналитических расчетов вероятности «пересечения»: 1 – расчетные значения, полученные по формуле (1); 2 – эмпирическая функция распределения времени до «пересечения»; 3 – расчетные значения, полученные по формуле (3);

4 – расчетные значения Q _В|_АБ1 ( τ ); 5 – расчетные значения Q _В|_АБ2 ( τ );

6 – расчетные значения Q _В|_БА1 ( τ ); 7 – расчетные значения Q _В|_БА2 ( τ )

Как видно из рис. 7, полученная нами кривая Q _В ( τ ) (линия 3) хорошо описывает стохастическую зависи-мость (маркеры 2). Линия же 1, построенная по значениям формулы (1), в целом не отражает исследуемое явление.

Линия 4 показывает изменение вероятности того, что «пересечение» произойдет, если событие А, возникнув первым, успеет полностью просуществовать в течение периода наблюдения. Как видно, на участке от 0 до 0,75 года данная вероятность равна нулю. Действительно, на данном участке длительность события А (0,75 года) оказывается больше, чем τ . Поэтому здесь событие А не может полностью просу-ществовать.

Линия 5 отображает изменение вероятности того, что «пересечение» произойдет, если событие А, возникнув первым, не успеет просуществовать в течение всей длительности. Данная вероятность на участке от 0 до 0,75 года возрастает: здесь увеличивается и вероятность возникновения А в течение τ , и вероятность возникновения Б, пока А еще длится. Однако после 0,75 года величина Q В|АБ2 ( τ ) снижается: период наблюдения начинает превышать длительность события А, и вероятность того, что А не сможет полностью просуществовать, стано-вится все меньше.

Аналогично ведут себя вероятности Q В|БА1 ( τ ) и Q В|БА2 ( τ ), изменение которых описывается линиями 6 и 7.

Отметим, что лишь на участке от 0 до 0,25 года, где длительности события А и события Б превышают период наблюдения, графики 1, 2 и 3 совпадают. Лишь на этом участке формула (1) дает результаты, согласующиеся с данными опыта. Выведенная нами зависимость для Q _В ( τ ) описывает процесс при любых значениях Δ τ A , Δ τ Б , Т А и Т Б .

Таким образом, показано, что для определения вероятности одновременного возникновения независимых случайных длящихся событий А и Б перемножение их вероятностей отличается от результатов стохастического моделирования. Подход, основанный на перемножении вероятностей, приводит к завышению результатов. При этом завышение оказывается тем значительнее, чем меньше дли-тельность рассматриваемых событий. Предложенное нами математическое выражение для вероятности «пересечения» независимых случайных длящихся событий достаточно точно описывает данные стохасти-ческого моделирования, а значит правильно отражает моделируемый процесс.

Подчеркнем, что полученная аналитическая зависимость справед-лива только для идеализированных явлений, которые полностью подчиняются экспоненциальному закону распределения. Поэтому перед применением полученных выражений необходимо строго обосновать, что закон распределения отказов, аварий и других событий, инициирующих пожары и взрывы, является экспоненциальным. Для оконча-тельного вывода о том, что полученное выражение правомерно использовать применительно к реальным процессам, необходимо сравнение аналитических результатов со статистическими данными об отказах, авариях, пожарах и взрывах и провести анализ погрешности.