Аналитическое исследование температурного поля поверхностного слоя валков горячей прокатки алюминиевых сплавов

• ¹    Самарский государственный аэрокосмический университет,

• 2    Волжский филиал Института металлургии и материаловедения им. А.А. Байкова РАН, г. Самара

Получено аналитическое решение уравнения теплопроводности для вращающегося цилиндра, подверженного циклическому нагреву в контакте с горячим металлом и последующему охлаждению поверхности эмульсией. Данное решение доведено до рабочей методики расчета температур в зависимости от числа оборотов валка и режимов прокатки для рабочих циклов и пауз между пропусками полос. Рекомендации по стабилизации тепловой выпуклости и доотпуску штатных валков в первой клети для повышения их эксплуатационной стойкости могут быть использованы в практике прокатного производства.

Температурный режим поверхностного слоя валков горячей прокатки алюминиевых сплавов определяет как качество горячекатаных полуфабрикатов (плит, полос и рулонов), так и срок службы валков и зависит от целого ряда технологических параметров процесса прокатки и условий охлаждения валков.

В процессе прокатки поверхностный слой рабочих валков прокатного стана подвергается циклическому нагреву в контактной зоне и последующему эмульсионному охлаждению при выходе из контакта на каждом обороте валка. Амплитуда колебаний температуры в течение оборота с удалением от поверхности валка интенсивно уменьшается, и на некоторой глубине становится равной нулю. В более глубоких слоях она при длительной прокатке монотонно возрастает. В паузах между пропусками полос охлаждение эмульсией приводит к снижению температуры как в поверхностном слое, так и в более глубоких слоях валка.

Детальное систематическое исследование температурного поля активного поверхностного слоя, а так же глубинных слоев валка экспериментальными методами трудно осуществимо. Поэтому в данной работе, используя общие подходы к решению подобных задач [1, 2], приводятся расчетные методы и их результаты применительно к реальным режимам эксплуатации валков горячей прокатки алюминиевых сплавов многоклетьево-го стана 2800 [7].

Используя аддитивные свойства интегралов уравнения теплопроводности, температурное поле в валке рассматривается как сумма температурных полей от отдельных тепловых потоков. Результирующую температуру в момент контакта валка с горячим металлом обозначим через t’, а при отсутствии контакта через t= t» -t’», где t»- температура, обусловленная потоком тепла в массу валка, накопленного тонким его поверхностным слоем в очаге деформации, t’»- температура, обусловленная потоком тепла с поверхности валка при его эмульсионном охлаждении. В расчетах температурных полей используются следующие общепринятые обозначения:

• X - коэффициент теплопроводности,

а - коэффициент температуропроводности, р - плотность тела, с - удельная теплоемкость, к - коэффициент теплопередачи

(вт/м2град), х - расстояние от поверхности (м), тс - время контакта (сек),

• V- скорость прокатки (м/сек).

Составляющая tпдля поверхности валка рассчитывается через коэффициент тепло-усвоения идеально контактирующих тел т и функцию передачи тепла от полосы к валку через тонкую пленку эмульсии G по формуле [1]

/         m t П = t 0 + Г G(t пол - t 0 ) , m +1

2т t " = 1 -------- п V т + Ат

^- t п ) ^exP

V

---x----

4 а (т + А т ) _у

а величина Ат находится из условия tП = tП при т = 0. Выразив время через число оборотов т = т об ■ n = nD в / V m =

( ^ G p ) пол \ ^{( Х} с Р ) вал

для случая однократного контакта валка с металлом на первом обороте, получим температуру от потока тепла на глубине х

G = 1

-

^f к exp -

V

² a т пол с

X

пол

А f erfc / ^V

kja т пол с

^Х пол

A

/

индекс “ пол ” - относится к прокатываемой полосе, а “ вал ” - к телу валка.

Усреднив теплофизические свойства алюминиевых сплавов и валковых сталей и

//       (tП,(р   tП,(0))      f Р А tx = A I------Т   expl        л 2

V n+A2 V n+A J где в = x2   = x2 V

⁴ a ^т об     ⁴ a ^{n D} в ’

приняв время контакта т _с= 0,08 - 0,01 с; к = 50^10 4 вт/м ² град при 8 = 1 - 2 мкм [1], получим т =2,077, т/(т+ 1) = 0,675, G=0,96, h =Gm/m+1=0,65. Применительно к непрерывному процессу прокатки под т ₀ будем понимать температуру поверхности валка перед входом в очаг деформации. Тогда для любого числа оборотов валка n получим

A = - b- = 0,302 4 ^ h п^ об Dd₆

тоб - продолжительность одного оборота валка;

A h - абсолютное обжатие в данном проходе.

Для поверхности валка при x=0

t П₍ n ) = ht 0 + (1 - h ) t П ( n - 1) .           (1)

//

// _     ^{( t}П ,⁽1)     t П ,⁽0) )

t^П = А I -----7Г ,.            ⁽³⁾

V n + A

При вычислении составляющей t» момент окончания нагрева поверхности от контакта с полосой т = т _с рассматривается как начальный момент распространения тепла вглубь валка от мгновенного плоского источника, интенсивность которого согласно [2,3] равна:

Отрицательный тепловой поток q эм , обусловленный охлаждением эмульсией, имеющей температуру 1_эм, будем считать постоянным и равным значениям [3]:

q ЭМ = a ^{[ t} П   ⁽ t ЭМ    t H ^{) ]          (4)}

Температурное поле, обусловленно е этим потоком, описывается формулой [2]

„ Xcp , , q = 2J    (t П у п

^- t п ) \к .       (2)

Процесс распространения тепла от такого однократно действующего источника при нулевой начальной температуре в теории теплопроводности описывается формулой [3]

где

Л" _ ² qЭМ ^т Д ^x пх р F V 2 40т )

' x ²      '

= exp--

+ А т )     V ⁴ а( т + А т ) ,

Тогда

t " =         q

J пХ с р ( т

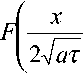
А

/ x ² ) = ^exp

4a т

V У

- п

xx ъЕI' erfгЕу

x erf 2 Дит - табулируемая функция

интеграла вероятности,

tП - средне интегральная результирующая температура поверхности валка t n = k1 (tn - t П ) ’ k1 - коэффициент осреднения, равный k1= 1,05-1,10.

Совместное решение уравнений (4) и (5)

при х = 0 дает выражение:

^tП ,( n )

где

/// t_П

2 ак 4т     ^

I—. —f₁ 2 ак 4т ^ V^{1 +} ж J

t n

V

-

tЭМ

-

t H

k

сти

Результирующая температура поверхно-(без начальной температуры tН) от еди-

ничного теплового источника q и охлаждения эмульсией q_ЭМ будет равна:

t   "_t"'= ___¹___P/+ ^k¹

t n t n t n         ptn ⁺ I ----7---------x

2^        ок_кT

/^    п/c/ 1 ₁

t 3M t H

.

V

к

Выразив время т через число оборотов n и обозначив

= A^t n .. . )

k = 1

^D ( n - k + 1)

^tn ,( k - 1)

^D ( n - k + 1) ^]+ t 3 - Н

Нn

-----;= + I h 1 + н4п

4n - k + 1 + A ² (1 + H4n - k + 1)"

После аналогичных преобразований температура на глубине х перед входом в очаг деформации выразится формулой:

^tx ,( n )

= а ^К 'П. k )

k = 1

^{- t}n ,( k - 1)

) D x ,( n - k + 1) ^]+ t 3-Н

Hn ■ F (n ) 1 + H4n

+ t_H

(9) здесь

D x ,( n - k + 1) = lexp^{( -} У ^{2 +} V^ H ^{(1 -} erfy )J D ( n - k + 1 ;

F ( n - k + 1) = exp^{( -} У ²) ^- V ^ y ^{(1 -} erfy );

^{2 ак} 'j^П Db _ „

—I    — = Н '

4 лА ср 4V

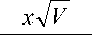
2 4 а л О в

W = 0,6218 4V при x=5 мм,

t ЭМ t H _ _t

= t Э - Н

к с учетом уравнения (3), получим

_ . V n,(l) - tn,(0) )     _nn_ n = ,n +a (1+Hn) 1+Hn -Н.(6)

В реальном процессе прокатки источник q действует многократно, т.е. при каждом обороте валка. Поэтому первый член в формуле (6) должен быть представлен многочленом, в котором каждое слагаемое k пропорцио- нально температурным напорам

/

Vt n,(k)    1 n,(k-1)/> длительность действия которых последовательно уменьшается за время одного оборота. Полная (с учетом начальной) результирующая температура поверхности валка перед входом в очаг деформации применительно к любому полному числу оборотов п = 1,2,3... выразится формулой:

= 2 ak 44D H = 0,00155 a

" 4nA c pv ’ W ^при D ^B =

=650мм; (12)

W y=vn^iTT                  (13)

Процесс прокатки каждой полосы N=1,2,3,… состоит из рабочих циклов длительностью n _p и пауз длительностью n _пз . В паузах тепловые источники q не действуют, поэтому при

(nр + nпз ) N - n пз + 1 ^ n < (n р + nпз ) N принимается tn(n) = tn(n-1) "                (14)

Тогда слагаемые сумм в формулах (7) и (9), соответствующие номерам оборотов в паузах, будут выпадать, так как для них

⁽ t n ( n ) - t n ( n - 1) ) = ⁰ "

Для любого угла поворота валка отно- сительно точки выхода из контакта с металлом (щ) в приведенных формулах вместо n

следует принимать n ^{1 +} 360 _O .

Формулы (7) и (9) справедливы для среднего сечения валка при прокатке широких полос или листов, когда тепловым потоком вдоль оси валка можно пренебречь. В сечениях близких к кромке проката с учетом продольного теплового потока в часть валка, не контактирующую с металлом, но охлаждаемую эмульсией, величина tП в каждом проходе составит:

^tП ,( n )

= A £ [ ( ' П« )

k = 1

^^^^^^^»

t П ,( k - 1) ) D ( n - k + 1) R ( n - k + 1) ^{] +}

^t x ,( n )

где

⁺ t Э - Н

^R ( n ) ⁺ t H ,

^ [(t П,(k)   t П,(k-1) )D,(n -k+1)R (n -k+1) ] + k=1

⁺ t Э - Н

^F(,n ) R ( n ) ⁺ t H ,

0,2 zW

^R ( n - k + 1) = ^{0,5 + 0,5} erf I ,   ₁

V n - k +1

так как остальные вычисляются ранее при последовательном расчете температур для меньших значений n. С учетом этого положения разработана программа расчета температурного поля в поверхностном слое валка на ПЭВМ. Расчеты выполнялись применительно к пятой и седьмой клетям непрерывной группы листопрокатного стана 2800. В расчетах принималось D _в = 640мм, t _пол = 400°С, t_ЭМ = б7°С, t_Н= 60°С .

Вследствие циклического нагрева от контакта с прокатываемой полосой на дуге захвата и последующего эмульсионного охлаждения поверхности, а также наличия пауз между пропусками полос, изменение температуры в точках поверхностного слоя рабочего валка носит сложный характер. Немонотонное изменение температуры в течение одного оборота с быстро затухающей амплитудой колебания при удалении от поверхности валка приведено на рис.1 . Расчеты значений температур в зависимости от угла поворота валка показали, что такой характер изменения температуры при прокатке по различным режимам распространяется примерно до глубины х = 5 мм (активный слой). На этой глубине и в более отдаленных точках (тепловое ядро) в рабочих циклах прокатки температура монотонно возрастает с каждым

z - расстояние от кромки листа до данного сечения, мм.

Для расчета температур по выведенным формулам для заданного числа оборотов n в силу их рекурентности необходим предварительный последовательный расчет температур для всех предыдущих значений п . В развертке сумм формул (7) и (9) комплекс (n-ck+ 1) меняется от п для первого члена суммы (k =1) до 1 для последнего члена (k=n). На первый взгляд кажется, что расчет по этим формулам требует значительного объема вычислений, связанных с определением всех (от k = 1 до k=n) значений коэффициентов D, D x и F при каждом новом обороте n.

Фактически, при данном n из всех значений ^D _(n - _k+1) , D _х , _(п - _к+1) и F _(п - _к+1) вновь требуется рассчитать только D _(n) , D _x(n) и F _(n) ,

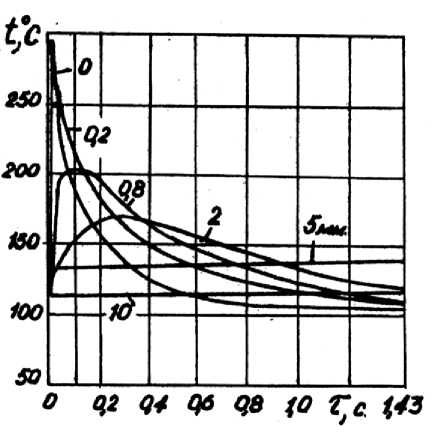
Рис.1 . Изменение температуры в поверхностном слое валка 0 640 мм в течение одного (шестого) оборота при прокатке второй полосы по режиму:

A h = 17 мм, V=1,4 м/с, а =9,700 Вт/(м 2 О С), n р =85, n пз =15.

оборотом валка. Рассчитанная по этой методике температура t _x на данной глубине может быть использована в качестве граничного условия для расчета температурного поля в тепловом ядре более простыми известными методами.

Дальнейшие расчеты производились для целочисленных значений n с определением температур поверхности на входе в очаг деформации (t_П), при выходе из него (t’_П) и температуры на глубине 5 мм (t_х). Они показали, что с увеличением числа оборотов n значения указанных температур в рабочих циклах прокатки непрерывно возрастают, но с затухающей скоростью. Во время пауз значения t_П и t_х снижаются также с замедляющейся скоростью постепенно приближаясь к t_ЭМ, но из-за их кратковременности далеко не достигая ее (рис. 2). При этом следует иметь в виду, что температура поверхности на каждом обороте циклирует между двумя соответствующими пунктирными линиями, что на рис. 2 не показано.

В процессе непрерывной прокатки полос N = 1,2,3,... со сравнительно короткими паузами между их пропусками через валки, как видно из рис.2, кривые изменения температур t_П, t_х ,t’_П от числа оборотов n распо-

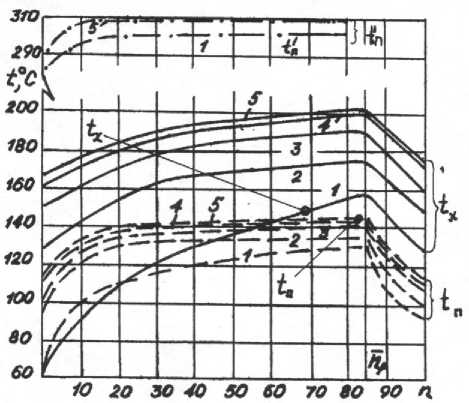
Рис.2 Зависимость температур поверхности валка ∅ 640 мм на выходе (t’ _П ), входе (t _П ) в очаг деформации и на глубине 5 мм (t_x) от числа оборотов (n) при прокатке полос N=1,2….5 gjрежиму: ∆ h = 17 мм, V=1,4 м/с, α =9,700 Вт/(м ^{2 О}С), n р =85, n пз =15.

лагаются одна над другой с нарастанием N, постепенно сближаясь, но не сливаясь полностью. Однако, учитывая погрешность в выборе значений исходных параметров для расчета и требуемую в практике точность в определении температур порядка 5-10°С, можно считать, что после прокатки 4...5 полос в активной зоне рабочего валка устанавливается квазистационарный температурный режим. К аналогичным выводам пришли авторы работы [2], экспериментально изучавшие тепловой режим работы валков. Установившийся температурный режим в тепловом ядре устанавливается значительно позднее.

Наибольший практический интерес представляют значения температур поверхности и на глубине 5мм для начала прокатки (конца пауз) (t_П, n _пз , t_х, n _пз ) и конца прокатки полос (t_П, n _р , t_х, n _р ) в квазиустановившемся режиме, наступление которого в дальнейших расчетах принято при прокатке пятой полосы. Для исследования влияния режимов прокатки и охлаждения на значения этих температур проведен расчет 24 вариантов температурного поля поверхностного активного слоя.

Расчеты показали, что на тепловой режим активного слоя оказывает влияние большое число параметров: абсолютное обжатие ∆ h, скорость прокатки V, интенсивность эмульсионного охлаждения, характеризуемая коэффициентом теплоотдачи α , длина прокатанной полосы выраженная числом рабочих оборотов валка n _р , длительность пауз τ _пз , представленная в расчетах числом оборотов валка в паузах n _пз = V τ _пз / π D_в .Влияние других параметров режима (t_пол, t_ЭМ, t_Н) не исследовалось, так как диапазон их изменения незначителен, и они принимались постоянными.

Наибольшее влияние на значения указанных температур оказывает абсолютное обжатие и скорость прокатки. Эта зависимость представлена графически на рис.3, который построен по данным расчета температур по разработанной методике при постоянных базовых значениях других параметров режима : nр =85, τпз ,=20с, α=7500 Вm/

(м ² град). Зависимость t_j,n где j=П,x , n = n _р ,

∆h nпз , от A = 0,3024   D при V=const в ис- в следованном диапазоне изменения ∆h - практически линейная, а от скорости V - имеет более сложный характер.

Раздельное влияние каждого из трех ос- тальных параметров i=nр , τпз , α на температуры tj,n(i) оценивалось коэффициентами Kj,n(i), рассчитываемыми по формуле:

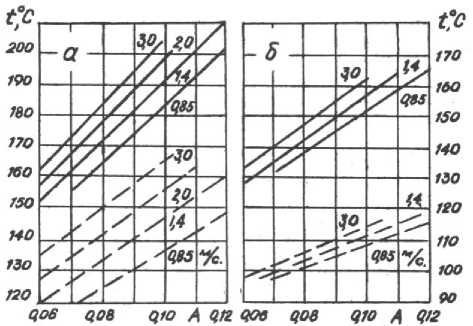
Рис.3. Зависимость установившихся температур поверхности (----) и на глубине

5 мм (-----) валка диаметром 640 мм в конце прокатки

K i , n ( i ) =

t _{j , n} ( i ) - t_ЭМ t_{j , n} ( i *) - t_ЭМ

в которой значения tj,n(i) определялись из температурного поля, рассчитанного для двух других, отличных от базового, значений параметров i. При этом для каждого нового значения i расчет температур tj,n(i) производился для двух - трех вариантов режима (сочетаниях основных параметров ∆h и V), для которых величина tj,n(i*) известна для базового значения i* и выбирается по графику (рис.3). Рассчитанные таким образом два-три Kj,n(i) для каждого конкретного значения i практически (с точностью до 3 %) совпадали. Рассчитано также не сколько вариантов режима одновременно с двумя новыми значениями i, отличными от базовых i*. Оказалось, что эффект попарного влияния параметров ( на Kjn(() незначителен (2-3 %) и им можно пренебречь, а совместное их влияние определять произведением значений коэффициентов K. п(г) для соответствующих i, каждо е из которых является однопараметрическим. Следует также отметить, что длительность рабочих циклов n р практически не влияет на температуры tП, nпз , и tх, nпз в конце пауз, а длительность пауз τпз (в диапазоне от 15 до 50 с) - на температуры tП, nр , tх, nр в конце рабочих циклов прокатки полос. В то же время интенсивность эмульсионного охлаждения а влияет на температуры как в конце прокатки, так и в конце пауз, причем более значительно полос при nр = 85 (а) и в конце пауз длительностью

Т пз = 20 с (б) от коэффициента обжатия

A = 0,302 4 ^{∆ h}

в

и скорость прокатки V (цифры у

кривых) для t_nan =400° С, t_H =60°С , t_ЭМ =67°С^О и а = 7500 Вт/(м ² град).

на температуры поверхности валка.

Графики зависимости коэффициентов K_j,n от параметров i представлены на рис.4. Используя их совместно с графиками на рис. 3, можно, не прибегая к расчету по формулам (1), (5), (7), определять значения искомых температур из формулы (16) при квази-установившемся режиме прокатки с достаточной для практики точностью.

При проведении технических расчетов необходимо знать коэффициент теплоотдачи

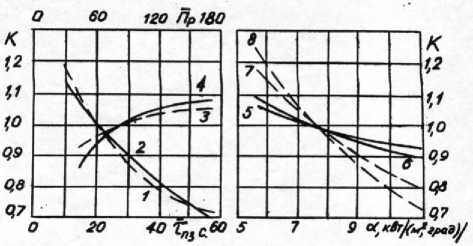
Рис. 4. Зависимость коэффициентов в формуле (18) от параметров режима прокатки и охлаждения :

^{1 К} n ( Т пз ), ²- К , П з ( Т пз ), 3- К п , n р ( n р ),

4- K_x , n р ( n р ), 5- K x П пз ( а ), 6- K x n р ( а ),

7- КпПр (а), 8 - Кп, Ппз (а), а при охлаждении поверхности валка эмульсией, подаваемой из спрейерного устройства (коллектора) под давлением через систему форсунок. Теплофизика и гидродинамика такого процесса весьма сложны; на величину а влияет большое число факторов: удельный расход охладителя, конструкция форсунок и их расположение по углу поворота и длине валка, расстояние от форсунок до поверхности, скорость вращения валка и пр. Расчет α по критериальным зависимостям, полученным в опытах по моделированию процесса спрейерного охлаждения различных объектов [4, 5 ], из-за сложности воспроизведения всех параметров процесса дает резко различные значения - от 2000 до 20000 Вт/{м2 град). Авторы работ [1, 6] рекомендуют α от 12000 до 16000 Вт/(м2 -град). В работе [8] приводятся обобщенные по станам холодной прокатки зависимости а от удельного расхода охладителя q при подаче его через форсунки круглой и щелевой формы различных размеров, при q до 5 л/м.с. Экстраполируя эти данные до значений 10-17 л/м.с, принятых на стане горячей прокатки 2800, получим соответственно α= 6000 + 11000 Вт/{м2.град). Температуры поверхности в конце прокатки полос, рассчитанные при принятых значениях aa, близки к выборочно замеренным на рабочих валках клети № 5 стана 2800 (125 - 145°С) при прокатке по различным режимам [7].

Рассмотрим некоторые практические приложения полученных результатов расчета. Важной характеристикой режима работы стана является устойчивость теплового профиля рабочих валков при прокатке полос по различным режимам и прокатке одной полосы, которая непосредственно связана с величиной изменения температуры t_x на поверхности теплового ядра (на глубине 5 мм). Анализ заводских данных по сочетанию параметров ∆ h, V, L( n _р ) технологических режимов прокатки разных сплавов показывает, что значение указанной температуры в конце прокатки полос ( t_x, n _р ) может изменяться от 170 до 215°С в клети № 5 и от 150 до 195 °С в клети №7 при α =7500 Вт/(м ^{2 .} град)=const.

Подчеркнем, что такие колебания температуры (следовательно, и теплового профиля) при переходе от одного режима прокатки к другому могут быть предотвращены (исключая крайние: самый легкий и самый тяжелый) соответствующим изменением интенсивности эмульсионного охлаждения. Однако в практике этот прием используется недостаточно в связи с отсутствием информации о зависимости теплового режима от режимов прокатки и охлаждения. Изменение температуры t_x , при прокатке одной полосы от начальной t_x, n _пз ( в конце пауз ) до конечной t_x, n _р (в конце прокатки полосы) также связано со стабильностью тепловой выпуклости и проявляется в продольной разнотолщинности листа. Анализ результатов расчета показывает, что увеличение темпа прокатки за счет сокращения длительности пауз и интенсификация охлаждения валков уменьшают разность температур ( t_x, n _пз - t_x, n _р ), повышают устойчивость теплового профиля и уменьшают разнотолщинность листа. Напротив, длительные паузы и простои, связанные с нарушением ритма прокатки, дестабилизируют тепловой режим и снижают качество листа по разнотолщинности.

Полученные данные о значениях температуры поверхности валка в контакте с полосой tʼП позволяют судить о соответствии материала валков и температуры их отпуска после закалки условиям эксплуатации. В клети № 5 при температуре полосы 400°С ее значение, соответствующее наиболее тяжелым тепловым режимам прокатки, составляет 320 - 325°С. Отпуск штатных валков при 340°С обеспечивает их структурную стабильность в этих условиях. Рабочие валки реверсивных клетей №1 и №2 имеют более высокую нагрузку, так как температура слитков ряда марок алюминия и сплавов на его основе составляет 450°С, а абсолютные обжатия принимаются 30 - 40 мм в клети №1 и 45 - 50 мм в клети №2. Кроме того, при первых проходах в клети №1 эмульсионное охлаждение валков отсутствует. Дополнительные расчеты, проведенные для ∆h=40мм, V=1м/с, nр= 3 и α = 0 дают tʼП =360°С при tʼпол=450°C. При увеличении температуры слитка до 500°С температура поверхности валка возрастает до 385°С. С ростом температуры разогрева поверхности растет и амплитуда ее колебания в течение оборота валка и пропуска слитка. Поверхность отпущенных после закалки валков при 340°С в этих условиях теряет структурную стабильность в процессе доотпуска при разогреве ее до указанных температур и быстро выходит из строя по трещинам. Температуру отпуска рабочих валков реверсивных клетей рекомендовано повысить до 380 - 400 °С.