Аналитическое моделирование поведения теплового поля для случаев радиальной и линейной фильтрации в околоскважинном пространстве

В работе рассматривается аналитическое моделирование поведения теплового поля в скважине для случаев радиальной и линейной фильтрации в упругой среде [1–3]. Радиальная фильтрация возникает при движении флюида в радиальном пространстве вокруг

Батманова Ольга Викторовна старший преподаватель Института информационных систем и инженерно-компьютерных технологий (ИСИКТ), заместитель заведующего кафедрой телекоммуникационных систем и информационной безопасности, Российский новый университет, Москва; старший преподаватель факультета финансов и банковского дела, Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации, Москва. Сфера научных интересов: геофизические и гидродинамические исследования скважин, системный анализ, анализ данных, информационные технологии, искусственный интеллект. Автор восьми опубликованных научных работ. SPIN-код: 1120-9070, AuthorID: 998517.

скважины вследствие негерметичности цементного камня, Сравнение динамики изменения температуры в зависимости от геометрических особенностей канала, по которому дренируется флюид, позволит понять, какие основные характерные признаки поведения теплового поля можно регистрировать, чтобы дифференцировать тип перетока [4–5].

Аналитическое моделирование поведения теплового поля для случаев радиальной ...

Аналитическая модель теплового поля в случае радиальной фильтрации

Для решения задачи поведения теплового поля при радиальном течении флюида вдоль оси скважины примем в качестве допущения влияние краевых эффектов на стенку скважины, пренебрегая радиусом скважины r, и установим его значение 0 м. Система «скважина – канал перетока» представляет собой полнотелый цилиндр радиусом R, через который движется флюид объемом Q. Флюид имеет объемную теплоемкость с _γ , коэффициент теплопередачи между породой и цементным кольцом обозначим α и собственную температуру T ; окружающее пространство имеет температуру Т г (геотермическая температура), которая меняется с изменением глубины от T ( z ) до T ( z + dz ).

На Рисунке 1 представлено схематическое построение рассматриваемой области движения флюида при радиальной геометрии потока. Мы не учитываем различие потока в стволе скважины и заколонном пространстве, полагая что движение происходит с одинаковой скоростью, а толщиной эксплуатационной колонны можно пренебречь.

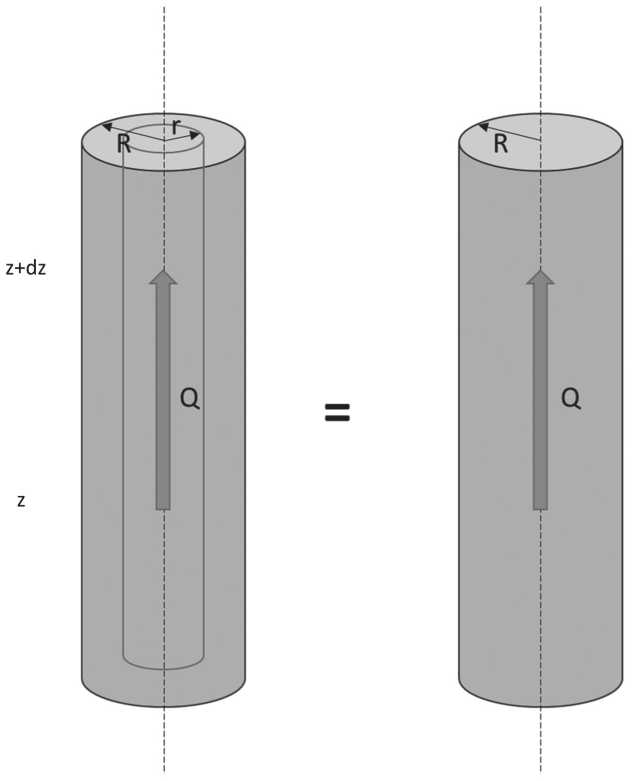
Рисунок 1. Схема объекта системы переноса флюида.

Источник: здесь и далее схемы и графики составлены авторами.

Поток флюида объемом Q проходит через цилиндр радиусом R , двигаясь вверх с глубины z ( z = 0) до z + dz . При этом меняется температура флюида с T ( z ) до T ( z + dz ) вследствие теплообмена с окружающей материей.

Динамическая схема процесса массопереноса представлена на Рисунке 2.

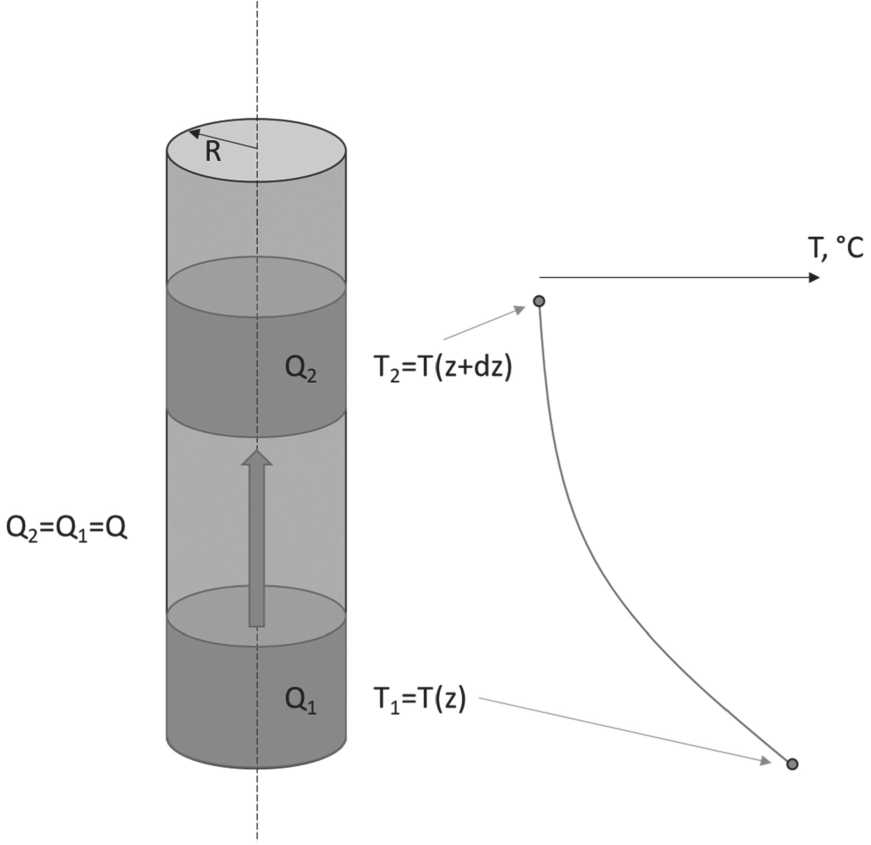
Рисунок 2. Динамическая схема процесса массопереноса в радиальном канале фильтрации

Запишем уравнение теплового баланса для процесса теплообмена флюида, текущего в пористой среде с окружающими горными породами.

В свою очередь, параметр а представлен уравнением а = / Q \.

(T—T)

Смысл коэффициента теплоотдачи заключается в характеристике интенсивности теплообмена между системами.

Изменение температуры по радиусу от стенки скважины происходит по линейному закону (Рисунок 3).

На графике нанесены три точки. Крайняя левая точка соответствует температуре на стенке скважины rc , следующая точка – значению температуры на произвольном расстоянии от стенки скважины в интервале r е (rc;т6Я). Чтобы найти температуру в соответствующем интервале между скважинной и геотермической температурой, необходимо воспользоваться уравнением

Аналитическое моделирование поведения теплового поля для случаев радиальной ...

T = Т г + ( T m - Т г )

ln I — к ^Г 6Л ln f r^ r ' вл

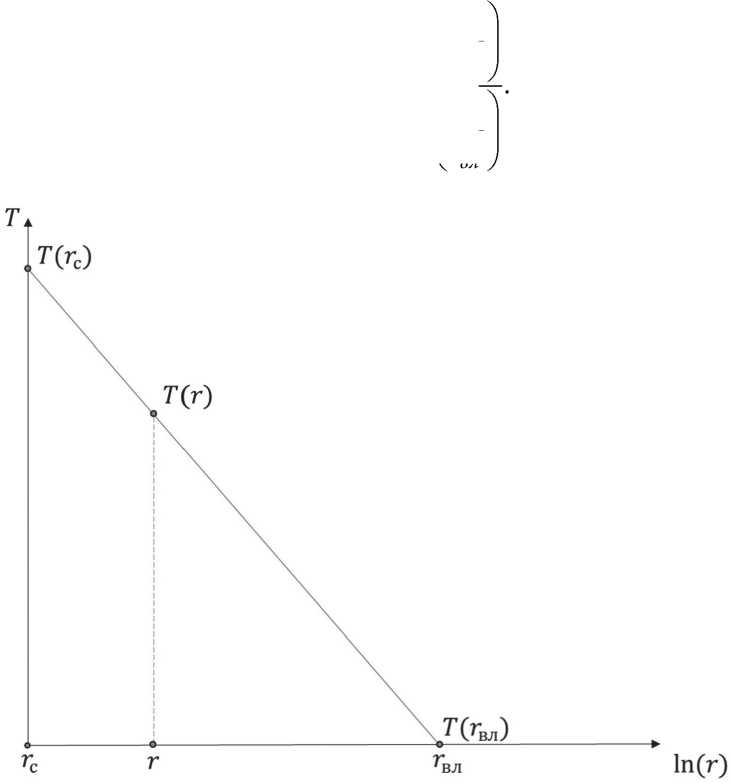
Рисунок 3. Изменение температуры по радиусу. В точке радиуса влияния измененное тепловое поле выходит на начальную пластовую температуру

Совместив уравнения (2) и (3), получим закон для нахождения величины дебита потока по тепловым изменениям на расстоянии r от стенки ствола скважины:

dT ^{Л (} Tc m ^{- Т} г ) 1

Q = Л--=--

dr

X

.

ln Р y

r c

Далее произведем замену величины дебита Q в уравнении (2) на выражение (4). Получим уравнение, описывающее коэффициент теплоотдачи как функцию теплопроводности горных пород X :

Л

.

a = S—^V r | ln (rc)

Yc к ln ( Твл )

Далее вернемся к уравнению (1) и произведем замену величины коэффициента теплоотдачи на выражение (5):

Л cYQ(T(z + dz)-T(z)) = 2^'c f 3 ( . X (T-Тг )dz. r I ln ( rc ) ] c к ln ( Гвл ) J

Произведя математические преобразования, выразим произведение, характеризующее изменение температуры относительно величины геотермической температуры с изменением глубины. Формула, описывающая данное выражение, представлена в уравнении

c rQIn(rc /r„ ) =(T-T)

2 пЛ        dT / dz '

Левую часть уравнения (6) можно обозначить буквой В ; данный параметр принято называть нормированным коэффициентом теплоотдачи. Итоговый вариант формулы (6)

представлен выражением

c / Q In ( r_c / r _en )

Br =------------

2пЛ

.

Аналитическая модель теплового поля в случае линейной фильтрации (Рисунок 4)

Рисунок 4. Динамическая схема процесса массопереноса в линейном канале фильтрации

Для решения задачи оценки поведения теплового поля при течении флюида по радиальному каналу фильтрации зададим начальные условия.

Поток флюида, дебит которого составляет Q , движется вверх по системе «скважина – трещина»; перемещение объема флюида происходит с начальной глубины z = 0 на расстояние z + dz . Трещина представляет собой прямоугольный блок с шириной _д x и протяженностью 2 L _mp . Ширина трещины пренебрежительно мала, условно примем ее равной 0.

Поскольку размеры трещины много больше радиальных размеров скважины, то в решении задачи оценки поведения поля при линейном канале фильтрации пренебрежем радиусом скважины и примем его равным 0 ( r c = 0 ).

По аналогии с аналитическим решением для радиального канала фильтрации составим уравнение теплового баланса для линейного канала фильтрации:

c , Q ( T ( z + dz ) - T ( z ) ) = 2 L m_P ( T - T , ) dz .                       (9)

В правой части уравнения (8) произведение 2 L _mp dz есть площадь канала фильтрации, поскольку в постановке задачи мы условились принять ширину фильтрационного канала равной 0.

Аналитическое моделирование поведения теплового поля для случаев радиальной ...

Поле температуры в случае линейного течения в пористой среде ведет себя аналогичным образом с радиальным течением в случае рассмотрения профиля температуры по ла-терали (Рисунок 5).

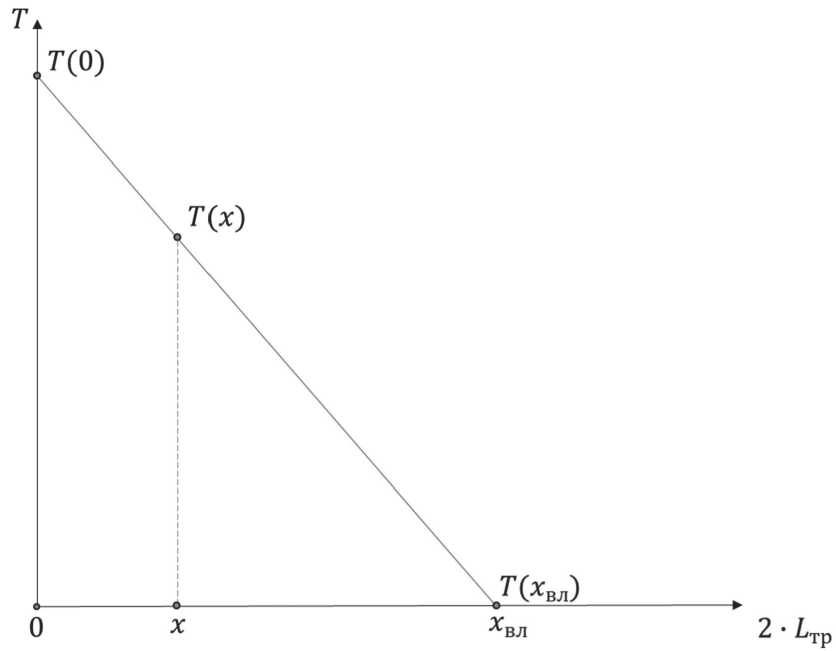
Рисунок 5. Изменение температуры по длине трещины. В точке радиуса влияния трещины измененное тепловое поле выходит на начальную пластовую температуру

На расстоянии x от центра скважины, но в диапазоне полудлины трещины x е ( 0;2 L _mp ) поведение температуры описывается формулой, являющейся полной аналогией формулы (3) для радиальной фильтрации флюида в пористой среде:

T = Т г + ( Т ст - Т г ) x ⁵^

- x

.

x en

Далее выразим коэффициент теплоотдачи α через коэффициент теплопроводности и радиус влияния трещины х _её . Запишем последовательно уравнение для потока флюида через трещину:

Q = -A dT .

dx

Для записи уравнения (10) в более развернутом виде необходимо найти производную температуры по координате x :

d ( ^Т ст dT = 0 +---- dx

dx

ст г . ^х ел

Полученное выражение объединим с уравнением (10), тем самым получим развернутую связь изменения температуры в зависимости от дебита, а также теплопроводности горной породы и радиуса влияния трещины:

Q = Мг «»

—

T)

.

^х вл

Поскольку уже ранее было записано выражение для коэффициента теплоотдачи в случае радиальной фильтрации (уравнение (2)), то запишем уравнение для коэффициента теплоотдачи для случая линейной фильтрации:

A

a =—.

x

вл

Когда известна связь между коэффициентом теплоотдачи и теплопроводностью горной породы, а также радиусом влияния трещины, можно записать нормированный коэффициент теплоотдачи для случая фильтрации флюида по трещине. Для этого запишем уравнение (8) совместно с уравнением (13):

cQ ( T ( z + dz ) — T ( z ) ) = 2 h^ t — T ) dz . (15)

^Х вё

Имея в виду тот факт, что нормированный коэффициент теплоотдачи имеет смысл уравнения (7), произведем перестановку переменных в уравнении (14) для получения искомой величины:

c y Ox eA B            .

f 4 L mp A

Имея зависимости, представленные коэффициентом теплоотдачи для двух случаев – радиальной фильтрации и линейной фильтрации, – можно провести их.

В первую очередь, примем во внимание, что для радиального канала фильтрации радиус влияния в зависимости от времени будет описываться логарифмической зависимостью гвл = lnl 1 +       I-                                             (17)

I    rc )

В свою очередь, при линейной фильтрации радиус влияния трещины будет рассчиты- ваться как хвл = Vet -

В обоих уравнениях фигурирует время влияние фильтрации t и температуропроводность массива горных пород.

Произведем замену в уравнениях (7) и (15) соответствующих радиусов влияния и запишем в виде уравнений c/1

Br =-

B f =

2nA

CyQ - -Jot

4 L mp A

.

Если найти отношение двух нормированных коэффициентов теплопередачи, то получим выражение

Аналитическое моделирование поведения теплового поля для случаев радиальной ...

B r

B f

Аналитически видно, что на ранних временах тепловое поле изменяется более интенсивно при радиальной фильтрации, нежели в случае линейной фильтрации флюида в среде (Рисунок 6).

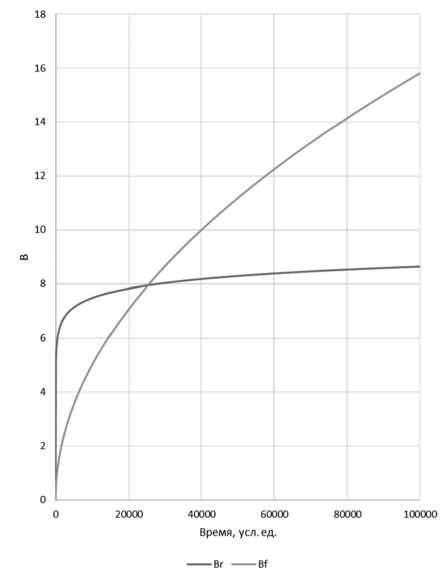
Рисунок 6. Изменение величины нормированного коэффициента теплопередачи во времени в зависимости от типа фильтрации

Выводы

Решение задачи, связанной с аналитическим моделированием поведения теплового поля для случаев каналов фильтрации различной геометрии, показало, что тип перетока проявляет себя по-разному относительно поля температуры. Анализируя динамику изменения нормированного коэффициента теплоотдачи В, можно сделать вывод, что при малом времени работы канала перетока заколонная циркуляция проявляет себя более интенсивно по сравнению с перетоком по трещине. Данная особенность соответствует физике процесса. Объем трещины и проводящих полостей в цементе различен, трещина уводит воду в пласт по латерали, что в результате оттягивает эффект яркого охлаждения прискважинной области. В свою очередь, при движении перетока по каналам в цементе интенсивно охлаждается прискважинная область. Данные особенности поведения температуры могут использоваться в качестве диагностических признаков оценки типа пере- тока, в зависимости от чего проводятся различные действия для предотвращения непроизводительной закачки вследствие межпластового перетока. Для ликвидации перетока по заколонному пространству в скважинах проводятся ремонтные работы, а для ликвидации перетока по трещине необходимо снизить деление нагнетания.