Аналитическое обеспечение учетного процесса: практика применения элементов математической логистики

С развитием аналитических методов современный бухгалтерский учет все больше становится похож на прикладной раздел математики. Сама сущность понятия «бухгалтерия» ассоциируется у простого обывателя с вычислениями и расчетами. Таким образом, применение математических методов есть логическое следствие развития данной отрасли человеческих знаний.

В данной статье речь пойдет о довольно сложном понятии – математической логистике. Дело в том, что обоснованные логистические расчеты лежат в основе любого успешного предприятия. Но многие специалисты считают, что бремя бухгалтерского дела и так слишком тяжело для современного бухгалтера. Имеет право на существование и другая точка зрения.

С развитием мирового хозяйства и информационных технологий, все больший удельный вес в учетном процессе будут занимать автоматизированные системы учета (АСУ) и анализа. Из этого можно сделать вывод о том, что высокотехнологичной экономике попросту не будет нужен бухгалтер, который не владеет методами анализа и аналитическими программами обработки данных. Но, мало просто уметь нажимать на клавиши и видеть результат в виде конечных цифр, очень важно понимать сущность процессов, происходящих внутри вычислительной машины. Это значит, что в современных условиях рыночной экономики должен произойти симбиоз трех направлений, которые впоследствии войдут в профессию бухгалтера – это фундаментальные знания бухгалтерского учета, экономического анализа и элементов программирования. Именно такие высококлассные специалисты в обозримом будущем станут двигателем экономики и поглотят излишнюю дифференциацию экономических специальностей.

Теперь, непосредственно, перейдем к нашему сквозному примеру. Допустим, что в городе Курске имеется некое производство. В состав данного комплекса входит бухгалтерская служба (экономического отдела и отдела планирования попросту нет). Перед бухгалтерами данного предприятия стоит острый логистический вопрос о наиболее дешевой доставке, необходимых для производства ресурсов, из некого завода, назовем его завод «В». Предположим, что через город Курск (точка А) по прямой l проходит железная дорога (рис. 1).

А

Рисунок 1 – Железная дорога и город Курск

Пусть, на расстоянии а (км) от железной дороги расположен завод «В» (рис. 2).

В

la

А

Рисунок 2 - Расположение завода относительно города Курска

Известно, что от завода «В» до железной дороги и до города Курска ведут множество автомобильных дорог, при чем, можно доехать как напрямую из завода «В», так и сначала по шоссе, а затем по железной дороге (рис. 3).

В

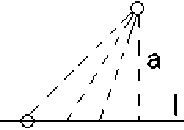
А С К D

Рисунок 3 - Множество дорог до города Курска

При этом, стоимость перевозок по шоссе в два раза дороже, чем по железной дороге. Необходимо построить такой маршрут, чтобы доставлять грузы из завода «В» в город Курск было экономически целесообразно.

Очевидно, что путь по шоссе (отрезок ВА) и путь ему противоположный будут очень дорогими, так как ВА2 = BD2+DА2. Заметим, что в данном случае нужно найти наиболее короткий и дешевый путь. Не сложно увидеть, что все протяженности дорог, заключенные внутри плоскости (ABD), существенно зависят от их угла наклона к железной дороге, а это значит, что существует перевалочный пункт (например точка С), так, что перевозка груза из завода «В» в пункт «С» по шоссе, а затем из пункта «С» в город Курск является наиболее дешевой. Отметим, что для примера мы могли взять любую другую точку в заданном интервале. Для решения поставленной задачи необходимо прибегнуть к детерминированному моделированию, то есть, построению математической модели экономического процесса.

Введем прямоугольную систему координат с центром в точке А, пусть точка D - проекция завода «В» на железную дорогу l; b - расстояние от Курска до точки D; а - угол между шоссе и железной дорогой; p - стоимость перевозки груза на расстоянии одного километра по железной дороге (рис. 4).

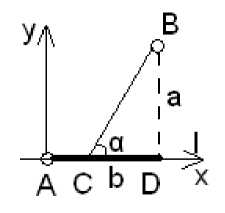
Рисунок 4 - Графическая модель

Итак, мы ввели графическую модель задачи, теперь выведем аналитическую модель. Рассмотрим некоторые соотношения в JBCD. Зная определения простейших тригонометрических функций найдем, что CD=аxсtg а (км), ВС= -^, АС=Ь - а^с1д а (км). Таким образом, найдем суммарную стоимость перевозки груза из завода «В» в город Курск (точка А), имея ввиду, что на каждом отрезке (ВС и АС) длину пути необходимо умножать на стоимость перевозки. Пусть у(а) - суммарная стоимость, тогда у(а) =p(b - а^с1д а) + ^^. Теперь применяя правила дифференциального исчисления, найдем производную данной функции:

dy_    ,    1   \ _|_ о -~ cos а . _ ра(1-2 cos а)

da  ^^Р  sin² а      ^paV sin 2 а         sin² а

Найдем стационарные точки данной функции из частных решений dy уравнения — = 0:

pа(1-2cosа)                                          1

---——; a---= 0, откуда 1 - 2cos a = 0 => cos a = - , где частное решение а= -, то есть АС= b - а*с1£ - = b - -р .

з ,                                з        Тз

Теперь, для того, чтобы ответить на вопрос поставленной задачи, найдем производную второго порядка:

d²y     2 sin axsin² a-(1-2 cos a)x2 sin axcos a

2 sin2 a-2 cos a+4 cos2 a

= ap--------------a--------------= ap sin3 a

угол а= - , получим:

1-cos a+cos2 a

= 2ap sin3 a

Подставим во вторую производную искомый

^4 |(a= - )= 2ap     >0

da² l^k      3 ^{7 p} ( V3 ) 3

Так как вторая производная положительна, то а= - есть то самое значение угла, при котором стоимость принимает наименьшее значение. А это значит, что нужно выбирать на карте такое шоссе, чтобы угол между ним и железной дорогой составил примерно 600, ибо при этом мы понесем наименьшие затраты при перевозке груза из завода «В» в город Курск.

Таким образом, разобрав наш условный пример, мы увидели всю важность основательных математических расчетов в хозяйственной деятельности предприятия. Пусть не пугают читателя сложные тригонометрические модели, ведь если наложить на проблему исследования технологическую плоскость в виде многочисленных вычислительных сервисов, то решение задачи заняло бы у обычного бухгалтера всего пару минут. А теперь представим, что 2 минуты не сложных расчетов позволят сэкономить предприятию десятки тысяч рублей за перевозку грузов. Согласитесь, вполне оправданная цена.

Итак, в заключении, отметим, что сегодня повседневная хозяйственная жизнь пронизана сложными задачами и ситуациями. Одни из них решаются просто, для решения других необходимо применять более сложные модели и методы. Но все они, так или иначе, могут быть решены с помощью современных вычислительных программ и математического аппарата.

Поэтому применение аналитических процедур различного рода, есть неотъемлемая часть профессионализма бухгалтера.