Аналитическое описание радиально и азимутально поляризованного света и моделирование преобразования поляризации с помощью субволновых ДОЭ

Острая фокусировка лазерного пучка необходима во многих задачах, таких как микроскопия, оптическая манипуляция микрообъектами [1,2]. Для получения светового пятна малого диаметра удобно использовать радиально-поляризованный световой лазерный пучок.

Как правило, лазерное излучение имеет линейную поляризацию. Для преобразования ее в поляризацию с осевой симметрией существуют различные методы. Например, в [3] предложен а оптическая схема для преобразования линейной поляризации в круговую путем сложения двух когерентных модовых пучков с помощью интерферометра Маха-Цен-дера. Авторы в [4] предлагают схему для преобразования поляризации лазерного пучка с использованием спиральной фазовой пластинки, так же с помощью интерферометрической оптической схемы. В [5] предложена схема, основанная на когерентном сложении модовых пучков с использованием фазовой дифракционной решетки, позволяющей менять межмодовый фазовый сдвиг без применения дополнительных элементов.

В [6-10] предложено использовать субволновые дифракционные решетки для поворота поляризации лазерного излучения. При падении поляризованного света на такую решетку поляризация поворачивается в зависимости от угла между направлением вектора поляризации падающего излучения и канавками решетки. Таким способом поляризацию падающего пучка можно повернуть от -π до π. В [9, 10] предложены формы рельефа дифракционного оптического элемента (ДОЭ) для формирования радиально или азимутально поляризованного пучка. Однако в данных работах не проводилось строгого моделирования распространения света с помощью таких ДОЭ.

В данной работе получены аналитические выражения для радиально и азимутально поляризованного лазерного пучка, формируемого путем сложения двух когерентных гауссовых оптических вихрей с круговой поляризацией. Показано также, что вместо гауссовых пучков можно использовать другие оптические вихри, в частности, гипергеометрические лазерные пучки , позволяющие формировать световое поле с радиальной поляризацией и комплексной амплитудой, пропорциональной ф ункци и Куммера (вырожденной гипергеометрической ф ункции).

Кроме того, в работе проведено моделирование распространения света через ДОЭ, рассмотренный в [10], а так же через ДОЭ, состоящий из четырех секций, каждая из которой поворачивает поляризацию падающего пучка на постоянный угол. Моделирование проведено при помощи программного пакета FullWAVE (фирма RSoft, США). Для анализа поляризации светового пучка на основе данных, полученных программой FullWAVE, разработана дополнительная программа на языке программирования C++.

1. Получение радиально и азимутально поляризованных пучков с помощью оптических вихрей с эллиптической поляризацией

На основе дифракционных интегралов Рэлея-Зоммерфельда в работе [11] получены выражения для распространения в свободном пространстве Гауссова оптического вихря с эллиптической поляризацией:

I Г I E x ( r , ф , 0 ) = B x exp I-- 2 I exp ( im ф ) ,

I to )

I r I

^E y ( r, ф ^,0 ) = B y exp l-- 2 I exp ( im ф ) , I to J

где ( r, ф ) - полярные координаты в начальной плоскости z = 0, to - радиус перетяжки гауссова пучка, m – порядок спиральной фазовой пластинки (топологический заряд), формирующей Гауссов оптический вихрь, B x , B y – амплитуды составляющих гауссова пучка E x и E y .

В произвольной плоскости, поперечной оптической оси, на расстоянии z комплексные амплитуды определяются след ующими выражениями:

E x , y ( p , 9 , z ) = ( - i ) m ⁺ 1

B_x , _ykz exp ( im 9 + ik4 p ² + z ²) c^

p ² + z^г

8 p 32 ex

■ Р (-У ) Im-1 ( У )- Im +1 (У ) ,

^E z ( p , ⁹ , ^z ) = ( ^- i ) m 2 ^k 2 ^exP p + z

'² + z ² + im 9 ) 8^ 3. ^ехР^{( -} У ^)x

X

f Bx

-

2 V

— exp ( i9) j( m + 3 - 3 У ) Im+1 ( У )-Im+3 ( У ) + У Im-1 ( У )-Im+5 ( У )

-

B X + iB y

exp (^- i ⁹) И ^{m + 1 - 3} У ) I m -1 ( У )^- I m +1 ( У ) ⁺ У I m - 3 ( У )^- I m +3 ( У )

-

^- i ( B x cos ^{9 +} B y sin ⁹ ) c p I m - ( y )^- I m +1 ( y ) I ,

где ( p , 9 ) - полярные координаты в рассматриваемой поперечной плоскости, к - волновое число,

ik

P = ~--1 ,   , , c =

®    2^ p ² + zz

k p        _ c ²

p^+z4p ’ ^y = 8P'

При B x = ± iB_y Гауссов пучок имеет круговую поляризацию, а при B_x ^ 0 , В_У = 0 - линейную.

В частности, для правой круговой поляризации B y = –i B x при m = 1, после перехода к радиальной и азимутальной составляющим из (2) получится

E r ( p , ⁹ , z ) =

E Ф ( p , ⁹ , ^z ) =

<

E z ( p , ⁹ , z ) =

- B x kzc Vn

8 ( p ² + z ² ) P ³² iB x kzc 4k

8 ( p ² + z ² ) P³² iB_xk 4k

8 ( p ² + z ²) P ³²

^exp ( ^ik4 p ² + z ^{2 -} У ) [ 1 0 ( У ) ^- 1 1 ( У ) ] ,

^exp ( ik4 p ² + z^{2 -} y ) [ 1 0 ( y )^- 1 1 ( y ) ] ,

exp ( ik p ² + z² - y ) X

^X ( ( ^{2 - 3} У ⁺ ic p ) [ I 0 ( У )^- 1 1 ( У ) ] ⁺ У [ I ( У )^- I 2 ( У ) ] ) .

Аналогично, для левой круговой поляризации B y = +i B x при m = –1, получим

E r ( p , ⁹ , z ) =

B x kzc 4k      (гк 2

8 ( p² + z ² ) p 32 ^eXp⁽ ^P⁷⁷

• У ) [ I 0 ⁽ У ^{) -} I 1 ⁽ У ) ] ,

<

^E ф ⁽p , ⁹ , z ) =     iBxkzc /^3/ 2 ^eXP ( ^ik^ p ^{2 +} z²

8 ( p ² + z ² ) p^{32     v}

Ez(p,9,z)=8^wp2exp (ik ^^

• У ) [ I 0 ⁽ У ^{) -} I 1 ⁽ У ) ] ,

• -    У ) x

X{(2-3У + icp)[I0 (У)-I (У)] + У[I (У)-I2 (У)]}.

При сложении полей (4) и (5) формируется гауссов пучок с радиальной поляризацией:

Er ⁽p , ⁹ , ^z ) = 4 (p B x + z *² y^ P 32 ^exp ( ^ik ^ p ^{2 + z 2 -} y ) [ ¹ 0 ⁽ y )^{- 1} 1 ⁽ y ) J ,

^E _v( p , ⁹ , z ) = ⁰,

<

17 ( ex \       iBxk 4k

^E z ⁽p , ⁹ , z ) = ./2 x 23 -

4 p ² + z ² P

■32 ^exp ( ik 4 p ² + z ^{2 -} y ) ^x

X{(2-3У + icp)[I0 (У)-11 (У)] + У[11 (У)-I2(У)]}, а при их вычитании – с азимутальной:

E_r ( p , 6 , z ) = 0,

E ^{ф( р} ’ ^{6 z} ) = 4 ( PBx">  ^exP ( ^ik ^ ^p 2 ^{+ z} 2 - у ) ^ I ° ⁽ у ) - I i ⁽ у ^,

_ E_z ( p , 6 , z ) = °.

Лазерные пучки (6) были экспериментально получены в [3].

Световые пучки (7) используются в полых металлических волноводах, так как при прохождении через них такие пучки демонстрируют минимальные потери на стенках [12].

В качестве поля в начальной плоскости z = 0 не обязательно использовать гауссов пучок. Если вместо (1) записать

E x ( r , Ф , ° ) = ^B x A ( r ) ^eXP ( im ф ) , E y ( r , ф ,° ) = B y A ( r ) exp ( im ф ) ,

где A ( r ) – произвольная функция от радиальной координаты, применить преобразование Рэлея-Зом-мерфельда с приближением, использованным в [11], то для поперечных составляющих получатся следующие выражения:

E r ( p , ⁶ , ^z ) =

= B_x ( cos 6- i sin 6 ) D 1 ( p , z ) exp ( i 6 ) +

+ B_x ( cos 6 + i sin 6 ) D 1 ( p , z ) exp ( - i 6 ) =

= 2 B x D i ( p , z ) ,

^E ф ( p , ⁶ , ^z ) =

= B_x ( - sin 6- i cos 6 ) D 1 ( p , z ) exp ( i 6 ) +

+ B_x ( - sin 6 + i cos 6 ) D 1 ( p , z ) exp ( - i 6 ) = = °.

При получении (12) использовалось свойство функций D m ( p , z ), которые равны для m = -1 и m = +1.

Аналогично, пучок с азимутальной поляризацией получается вычитанием указанных пучков (11) с круговой поляризацией:

где

E x ( P , ⁶ , ^z ) = ^B x D m ( P , ^z ) ^exP ( im ⁶) ,

E y ( p , ⁶ , ^z ) = ^B y D m ( p , ^z ) ^eXP ( im ⁶) ,

E r ( p , ⁶ , ^z ) =

= B_x ( cos 6- i sin 6 ) D 1 ( p , z ) exp ( i 6 ) -

- B_x ( cos 6 + i sin 6 ) D 1 ( p , z ) exp ( - i 6 ) =

D m ( P , z ) = ( - i ) ” ⁺ 1

kz exp ( iksj p ² + z ² )

M

X J A ( r ) exp

ikr ²

p ² + z¹

12 v     J

m

X

k p r

1J

। rdr.

= °,

^E ф ( p , ⁶ , ^z ) =

= B_x ( - sin 6 - i cos 6 ) D 1 ( p , z ) exp ( i 6 ) -

- B_x ( - sin 6+ i cos 6 ) D 1 ( p , z ) exp ( - i 6 ) =

= - 2 iB x D i ( p , z ) .

После перехода к радиальной и азимутальной составляющим (9) примет вид:

E r ( p , ⁶ , ^z ) =

= E_x ( p , 6 , z ) cos 6 + E_y ( p , 6 , z ) sin 6 =

= ( B_x cos 6 + By sin 6 ) D m ( p , z ) exp ( im 6 ) ,

E ф ( p , ⁶ , ^z ) =

= - E_x ( p , 6 , z ) sin 6 + Ey ( p , 6 , z ) cos 6 =

= ( - B x sin 6 + By cos 6 ) D m ( p , z ) exp ( im 6 ) .

Как и в случае с гауссовым пучком, сложим два пучка: пучок (11) с правой круговой поляризацией ( B y = –i B x ) и m = 1, и пучок (11) с левой круговой поляризацией ( B y = i B x ) и m = –1. В результате получится пучок с радиальной поляризацией:

В качестве примера рассмотрим гипергеометрический лазерный пучок, возникающий при прохождении гауссова пучка с амплитудной степенной составляющей через винтовой логарифмический акси-кон с параболической линзой. В этом случ ае

I r I

A_r ( r ) = r exp--- X

I ® 2 )

2 ,

I ikr I I ■ 1 r I X exp--exp i у In—

I 2 f ) 4     r ° J

где to - радиус перетяжки Гауссова пучка, v - порядок амплитудной степенной составляющей, f – фокусное расстояние параболической линзы, у и r ° — параметры логарифмического аксикона.

В этом случае при сложении гипергеометрического пучка с правой круговой поляризацией и m = +1 с гипергеометрическим пучком с левой круговой поляризацией и m = –1 получится радиально поляризованное поле (12), для которого функция D 1 ( p , z ) имеет следующий вид:

D 1 ( p , z ) =

kz exp ( ik^ p ² + z² )

^ o^Y ( p 2 ⁺ z 2 )

X

X

f v + i Y+ 3 c Г

V 2

v + i y+ 3

4 p ²

f v + i Y+ 3   __c^3

1F1 I        ~       ;2; I, v 2        4 p)

где

1 ik ik              kp p p> + 2/ " 2,p .z’ c = 7p47

теристики первых двух: отсутствие решетки в области, близкой к отрицательной части оси X, скачок фазы на π, однако состоит из четырех отдельных зон, и световой пучок на выходе после него разделен на четыре сектора с однородной поляризацией в каждой из них. Межд у зонами присутствует скачок поляризации на 90°.

Цель моделирования была в нахожд ении минималь ной глуб ины рельефа бинарных субволновых ДОЭ для преобразования линейной поляризации в радиальную. Моделирование было проведено для

а 1 F 1 ( a ; b ; z ) – вырожденная гипергеометрическая функц ия (функция Куммера). Выражение (15) получено с использованием справочного интеграла (формула 6.631.1 в [13]):

следующих параметров: длина волны света λ = 1,55 мкм, показатель преломления решетки n = 3,47 (кремний). Период решеток на рис. 1 в наиболее частых областях составлял 0,21 мкм. У решетки, изображенной на рис. 1 а , в левой стороне наибольший период на краю ДОЭ составлял 2,37 мкм.

M j xц exp (-ax2) Jv (вx) dx = 0

_вт f У + Ц + 1 3

^p I 2 ) X

У+Ц+ 1

2 ^{V+ 1} a” r ( v + 1 )

X 1 F 1

f У + Ц+1 _

V 2 ^;

v + 1;

-

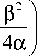
где Re( a ) > 0, Re( ^ + V ) > -1.

2. Моделирование

Так как задача преобразования поляризации падающего пучка ставилась для элементов микрооптики, то рельеф двух ДОЭ был позаимствован из [10] без изменений. Высота рельефа элемента на рис. 1 а рассчитывалась по формуле:

Рис. 1. Бинарные субволновые ДОЭ для преобразования линейной поляризации в радиальную

h

H

= —sgncos

C n nr ( x , y )

2 f 0 ( ^x , y ) 3

^{x cos} M^-1

V V 77

где h – высота рельефа в текущей точке с координатами x , y ; H – максимальная заданная высота решетки, r ( x , y ) - расстояние от центра элемента до точки с координатами ( x , y ) , 0 ( x , у ) - угол между осью X и вектором ( x , y ) , C =8/5 - константа, определяющая частоту полос дифракционной решетки, n - показатель преломления материала ДОЭ, sgn( x ) - знаковая функция.

Несмотря на большой относительно длины волны света период решетки, в левой части элемент а (рис. 1 а ) рабочие зоны решетки составляют значительную часть элемента. Элемент на рис. 1 б – то же, что и на рис. 1 а , но с отражени ем рельефа в левой части из правой. Такой элемент так же поворачивает поляризацию, однако между левой и правой частью выходного пучка имеется скачок фазы на π. Третий элемент (рис. 1 в ) исключает отрицательные харак-

Моделированием прохождения плоской волны с линейной поляризацией через элементы на рис. 1 была определена высота рельефа для данного показателя преломления света. Она составила h = 0,62 мкм (0,4 λ).

Элементы на рис. 1 преобразовывают линейную поляризацию в радиальную (вектор напряженности электрической составляющей поля колеблется вдоль радиальной полярной координаты) или азимут аль-ную (вектор напряженности электрической составляющей поля в точке колеблется перпендикулярно радиальной полярной координате) в зависимости от поляризации падающего пучка. При падении пучка с линейной поляризацией , когда вектор электрического поля находится в вертикальной плоскости, данные элементы (рис. 1) дадут азимутальную поляризацию. Если повернуть элемент на 90 градусов при неизменном положении вектора напряженности электрического поля, на выходе из элемента получится радиальная поляризация. Размеры элементов составляют 7×7 мкм. Для получения радиальной поляризации при моделировании ДОЭ на рис. 1 поворачивались на 90°.

Моделирование прохождения света через ДОЭ проводилось при помощи программного пакета FullWAVE. Для обработки данных, полученных с помощью FullWAVE, было написано дополнительное программное обеспечение на языке C++.

На рис. 2 приведены диаграммы распределения угла наклона к оси X вектора напряженности электрического поля в световом пучке после прохождения плоской световой волны через элемент на рис. 1 а . Вектор электрического поля падающего пучка был направлен вертикально для получения и радиальной (рис. 2 б ), и азимутальной (рис. 2 в ) поляризаций. Для получения радиальной поляризации ДОЭ на рис. 1 были повернуты по часовой стрелке на 90°. а) ^5"            A                   " 1 -3 -2 -1 0 '1 2 3          —тг б)                   жм 2 -2 -         Ж -3 -2 -1 0 '1 2 3          -л: в)                                .мим Рис. 2. Распределение угла наклона вектора напряженности электрического поля в выходном пучке после прохождения через элемент на рис. 2а: а) трехмерная модель ДОЭ, б) радиальная поляризация; в) азимутальной поляризация. Здесь и далее стрелками показано направление вектора электрического поля в один момент времени Как видно из рис. 2 б , таким элементом формируется радиальная поляризация. Это связано с тем, что в той части ДОЭ, которая находится близко к отрицательной полуоси X, вектор поляризации не должен поворачиваться. Поэтому чрезмерная величина периода решетки в данной области не сказывается отрицательно. Скачок с черного на белый цвет на этих рисунках и ниже соответствует изменению

угла наклона вектора напряженности электрического поля с –π на π, что фактически означает одно и то же направление данного вектора. При получении азимутальной поляризации (рис. 2 в ) на выходе ДОЭ на рис. 1 а в области близко к отрицательной части оси X субволновая дифракционная решетка почти отсутствует, что видно на рис. 1 б . Это влечет некорректный поворот поляризации, что видно на рис. 2 в в левой части близко к оси X. На рис. 3 приведены диаграммы распределения угла наклона к оси X вектора напряженности электрического поля в световом пучке после прохождения света через элемент на рис. 1 б . Выбором расположения ДОЭ относительно падающего пучка так же формировались на выходе радиальная (рис. 3 б ) и азимутальная (рис. 3 в ) поляризации. а) -3 -2 -I 0 7 2 3 б)                           А'' мим ^               --------1                              Л 2 - /- fl   T                    T           1 - 1      '                                * - 3 -                                       1 - 3 -2 -I 0 7 2 3         -7Г в)                            А-' мим Рис. 3. Распределение угла наклона к оси X вектора напряженности электрического поля в выходном пучке после прохождения через элемент на рис. 1б: а) трехмерная модель ДОЭ; б) радиальная поляризация; в) азимутальная поляризация

Формирование поляризации на выходе элемента на рис. 1 б происходит равномерно по всему полю, в отличие от элемента на рис. 1 а , что видно на рис. 3 а , б . Однако из рис. 3 б и рис. 3 в видно, что между двумя частями выходного пучка присутствует скачок фазы на π. Это связано с тем, что ДОЭ на рис. 1 б был получен из элемента на рис. 1 а путем отражения правой части рельефа. Избавиться от скачка фазы можно, если сделать дифракционный оптический элемент не бинарным, компенсируя скачок фазы на π при формировании рельефа, а со ступенькой.

На рис. 4 приведены диаграммы распределения угла наклона к оси X вектора напряженности электрического поля в световом пучке после прохождения света через элемент на рис. 1 б со ступенькой на π межд у правой и левой частями.

б)                         X', мкм

в)                        X', мкм

Рис. 4. Распределение угла наклона к оси X вектора напряженности электрического поля в выходном пучке после прохождения через элемент на рис. 4а со ступенькой между правой и левой частями: а) трехмерная модель ДОЭ; б) радиальная поляризация; в) азимутальная поляризация

Из рис. 3 и 4 видно, что добавление ступеньки высотой       межд у правой и левой частью ДОЭ

2( n - 1)

на рис. 1 б позволило получить радиальную и азимутальную поляризацию без скачка фазы на π межд у двумя частями выходного поля.

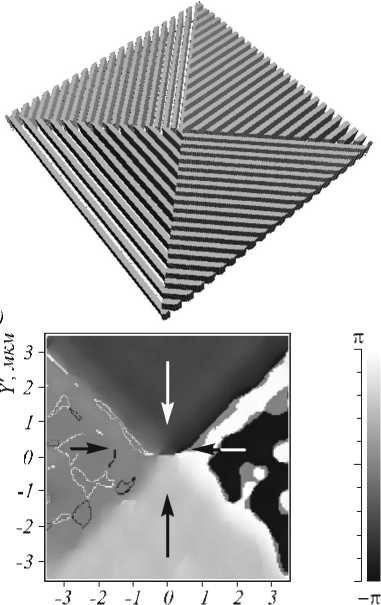
На рис. 5 приведены диаграммы распределения угла наклона к оси X вектора напряженности электрического поля в световом пучке после прохождения света через элемент на рис. 1 в .

б)                         X', мкм

в)                        X', мкм

Рис. 5. Распределение угла наклона к оси X вектора напряженности электрического поля в выходном пучке после прохождения через элемент на рис. 1в:

а) трехмерная модель ДОЭ; б) радиальная поляризация;

в) азимутальная поляризация

Световой пучок после прохождения через дифракционный элемент состоит из четырех частей с почти постоянной поляризацией внутри каждой части. Плоскость наблюдения при всех моделированиях, показан- ных на рис. 2-5, находилась на расстоянии 0,15 мкм от поверхности ДОЭ. Если отдалить плоскость наблюдения, границы между отдельными частями с постоянной поляризацией начнут размываться. На рис. 6 приведена диаграмма распределения угла наклона к оси X вектора напряженности электрического поля в выходном пучке после прохождения света через элемент на рис. 1в . Плоскость наблюдения находилась на расстоянии 3 мкм от поверхности ДОЭ.

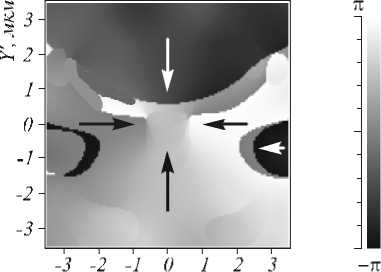
а)                        X', мкм

• б)                         X', мкм

Рис. 6. Распределение угла наклона к оси X вектора напряженности электрического поля в выходном пучке после прохождения через элемент на рис. 1в, расстояние между ДОЭ и плоскостью наблюдения 3 мкм а) радиальная поляризация; б) азимутальная поляризация

При прохождении некоторого расстояния четкие границы поляризации межд у отдельными зонами начинают размыв аться, что видно из рис. 6.

Заключение