Аналитическое определение интенсивности изнашивания бандажных полок рабочих лопаток ГТД

1Для улучшения газодинамических показателей и вибрационной прочности рабочие лопатки некоторых ступеней компрессора и турбины имеют бандажные полки. Эти полки образуют замкнутое кольцо на периферии рабочего колеса. Несмотря на значительный предварительный натяг, сжимающий полки соседних лопаток, последние не остаются неподвижными относительно друг друга при работе. Перемещение полок, вызванное вибрацией системы диск — лопатки, приводит к их взаимному трению и износу. Износ соприкасающихся поверхностей приведёт к ослаблению натяга, раскрытию стыка, что в свою очередь может вызвать разрушение лопатки и выход двигателя из строя. Таким образом, задача определения места и времени до раскрытия стыка является актуальной.

Для решения поставленной задачи необходимо знать    величины    динамических    реакций, возникающих в стыках полок и замке лопатки вследствие вибрации. Для этого использован приближённый аналитический метод.

Основным возмущающим фактором при вибрациях системы диск — лопатки считаем колебания диска. Полку представим как свободное абсолютно твёрдое тело, действие связей заменим их реакциями. На полку действуют следующие силы:  вес полки ; восстанавливающая сила упругости на конце лопатки ; силы натяга бандажа и , приложенные как реакции от соседних полок; сила реакции , возникающая в стыке, как в опоре от внешней нагрузки интенсивностью (аэродинамическая сила набегающего потока); силы трения и в стыках и момент сопротивления кручению .

Полка участвует одновременно в следующих четырёх основных движениях: вращательном вокруг оси вала вместе с диском *(t); колебательном вместе с замком лопатки в плоскости перпендикулярной       плоскости       диска

(t);колебательном в плоскости наименьшей жёсткости    относительно    замка    лопатки

(t);вращательном вокруг оси Сz (t).

При этом первые два составляют переносное движение, а два другие — относительное. В соответствие с этим положение полки определяют углы φ*, χ, ζ, β. Законы * и χ известны:

* t,

где - угловая скорость вращения вала.

Asin(m ) cos(pt),

Где согласно [1] A – амплитуда колебаний диска; m

–

число узловых диаметров, которые считаем неподвижными относительно диска; p – круговая частота колебаний диска.

Для определения законов движения (t) и β(t) использована теория Лагранжа и составлены дифференциальные уравнения движения полки:

J

+ ML  - M£ R + L J L sin /?о ^) cos Po +

+ % sin ₀      M R L L sin ₀ sin ₀ cos ₀

3 EJ

+ / sin/?Q J -(-—j^- N-N + fL 1 fLs sin/?q b3

N N f       ² L cos         qL ²,

1    22             0   8

b

Jz 1+ f + N 1-/3 = z ₂

b     GJp

N N fb N N               .

^{1            1 2        L}       (3)

где M – масса полки; L – длина пера лопатки; R – радиус диска; β 0 – угол закрутки пера лопатки; E – модуль упругости; J , J z - моменты инерции полки относительно оси наибольшей жёсткости и относительно оси z ; f – коэффициент трения; b – ширина полки; J p – полярный момент инерции сечения пера под полкой. Данные уравнения решаются численным методом на ЭВМ. Эти уравнения необходимы для определения сил инерции при расчёте динамических реакций.

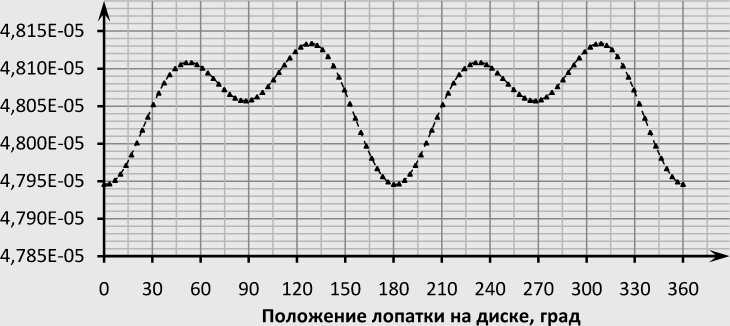
• 2    у. д.

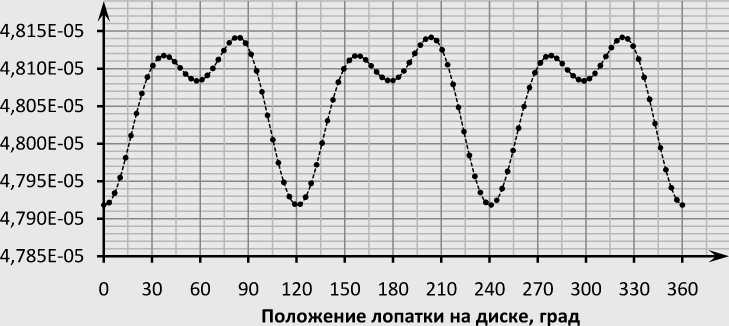
• 3    у. д.

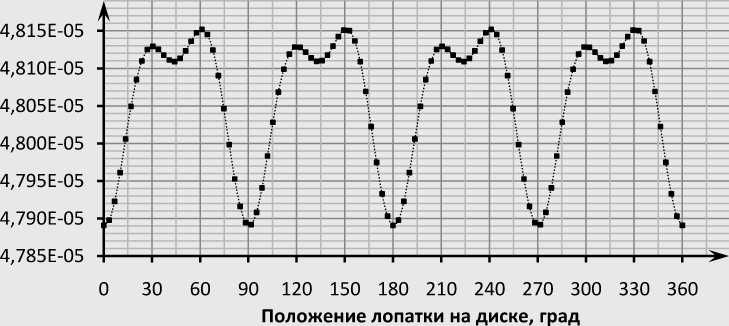
Рис.1. Линейная скорость изнашивания полосок по окружности диска

• 4    у. д.

Для определения динамических реакций использован метод кинетостатики. В результате получена система из шести алгебраических уравнений с шестью неизвестными:

a Nd + Xd + a 0, a Nd + Yd -х Zd + a0, a Nd + хYd + Zd + a0, a Nd + LYd -х R+ L Zd + M d sin β + a 0, a Nd LXd b хYd +Md cosβ + a 0, 92G,         010

a11N d +RXXd + Mzd + a12  0

где a1, a2…a12 – коэффициенты, зависящие от , β, χ и их производных; Nd – динамическая реакция в стыке полок; Xd, Yd, Zd, Md^ , Mdz – динамические реакции в замке лопатки. Решая данную систему на каждом шаге интегрирования дифференциальных уравнений (3), получим зависимость величины динамической реакции от времени.

JV

Anh

u0 -wPrKMKÔ ,

RT

Зная динамические реакции и площади контакта, можно вычислить скорость изнашивания.

Площадь контакта в каждый момент времени

где А r

– фактическая площадь контакта; h –

зависит от взаимного углового смешения контактирующих полок :

глубина необратимо повреждаемого слоя, мм; – исходная повреждаемость металла; X - общее число разрушаемых связей; t 0 =10^-13с – период колебаний

bc + 1b2L+R J- 3c 3§ 2

⁴                          (5)

4c L +R   2c2 + b2 -|8| ,

где c – толщина полки.

Объёмная скорость изнашивания, мм3/с, равна [2]:

атомной решётки; u 0 – энергия активации, Дж/моль; Y – структурно-чувствительный коэффициент, (Дж∙мм²)/(моль∙кг); V – коэффициент поглощения материала; P r – фактическое давление в области контакта, кГ/мм²; K M , K Ф – заданные коэффициенты; R – газовая постоянная, Дж/(моль∙К); Т – температура в области контакта, К.

Фактическое давление в области контакта P r

зависит от номинального P a , которое в свою очередь определяется как сумма давлений от динамической реакции N ^d и предварительного натяга q n

Nd

Pa          qn.

При этом линейная скорость изнашивания

JV h    Ar .

Для вычисления скорости

(8) изнашивания

необходимо интегрировать систему уравнений (3) на интервале от t = 0 до t = 0,1c, так как колебания

имеют периодический характер. Число шагов интегрирования n = 10000. На каждом шаге определялись динамические реакции, объёмная и линейная скорости изнашивания. Величина износа за 1 секунду определена как сумма произведений

n

Uhñåê  10 E Jhi •At, i 1                               (9)

где A t – шаг интегрирования, с.

Соответственно за 1 час износ достигнет

значения

U ÷àñ 3600 Uh .

Для расчётов взят диск радиусом R = 0,5 м со 106 лопатками длиной L = 0,142 м. Были получены линейные скорости изнашивания для каждого стыка бандажных полок. Расчёты проведены для случаев колебаний диска с 2, 3 и 4 узловыми диаметрами (у. д.). Полученные значения представлены в виде графиков зависимости линейной скорости изнашивания (мм/час) от положения лопатки на диске (рис. 1).

Как видно из графиков, наибольшая интенсивность износа наблюдается между узловыми диаметрами, т. е. там, где амплитуда колебаний, а, следовательно, и динамические реакции достигают наибольших значений.