Аналитическое определение места судна по двум измеренным расстояниям от навигационных ориентиров с помощью лазерных дальномеров (прямая засечка)

• 1.    Введение

• 2.    Два пути решения задачи

При производстве прибрежного промера и при тралении используется для определения места судна прямая засечка. Так как в настоящее время на вооружении гидрографов имеются лазерные дальномеры, то для аналитического определения места судна по двум измеренным расстояниям с навигационных ориентиров предлагается следующая схема расчета, выполненная на сфере (рис. 1).

Выбраны два навигационных ориентира А и В, на них находятся наблюдатели с лазерным дальномерами, которые одновременно измерили расстояние ДA и ДB, а на судне установлен лазерный отражатель. Если ориентиры А и В находятся в прямой видимости, то между ними измеряется расстояние с помощью лазерного дальномера, если нет видимости между знаками, то, имея точные координаты ориентиров А(ϕА, λА) и В(ϕВ, λВ), аналитически рассчитывается расстояние между ними (в градусной мере) по формуле sin2(S/2) = sin2((ϕB - ϕA)/2) + cosϕB⋅cosϕA⋅sin2((λB - λA)/2). (1)

Также предварительно рассчитываются направления с точки А на В и наоборот с точки В на А (рис. 1). Эти направления К А-В и К В-А определяются по формулам:

tg K A-B = sin( λ B - λ A )/(tg ϕ B ⋅ cos ϕ A - sin ϕ A ⋅ cos( λ B - λ A ),

tg K B-A = sin( λ B - λ A )/(sin ϕ B ⋅ cos( λ B - λ A ) - tg ϕ A ⋅ cos ϕ B ).

После этих предварительных вычислений, которые можно выполнить заранее, имея выбранные навигационные ориентиры, рассматриваем сферический треугольник АСВ, в котором три стороны известны.

Этих данных достаточно, чтобы рассчитать полупериметр треугольника Р , а также углы А и В по формулам:

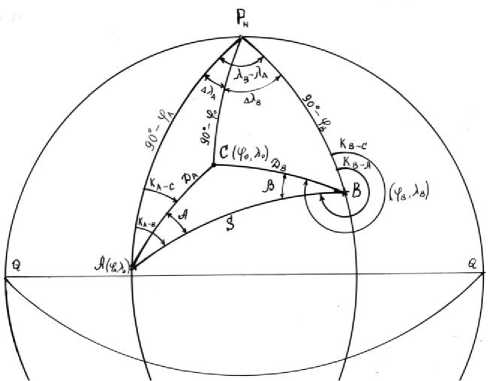
Рис. 1. Аналитическое определение места судна по двум измеренным расстояниям от навигационных ориентиров А и В

Санаев А.И., Пасечников М.А. Аналитическое определение места судна...

Р = (ДА + ДВ + S)/2,(4)

sin2(A/2) = (sin(P - ДА)⋅sin(P - S))/(sinДА⋅sinS),(5)

• sin2(B/2) = (sin(P - ДB)⋅sin(P - S))/(sinДB⋅sinS).(6)

После вышеуказанных вычислений можно определить направления К А-С , К В-С (ортодромические пеленги) с навигационных ориентиров А и В на точку С (судно). Они определяются по формулам:

КА-С = КА-В - А,(7)

КВ-С = КВ-А + В.(8)

Следовательно, имеются ортодромические пеленги К_А-С и К_В-С на точку С , а также измеренные расстояния Д_А и Д_В .

По этим данным на навигационном ориентире А , используя сферический треугольник АР_NС , направление К_А-С и расстояние Д_А , рассчитываются обсервованные координаты точки С (судна) по формулам:

sinϕ1 = sinϕA⋅cosДА + сosϕA⋅sinДА⋅cosKA-C, tgΔλ1 = (tgДА⋅sinKA-C)/(cosϕA - tgДA⋅sinϕA⋅cosKA-C),                   (9)

λ ₁ = λ _A + Δλ ₁.

Аналогично на точке В из сферического треугольника СР N В по К В-С и расстоянию Д В рассчитываются обсервованные координаты ϕ ₂, λ ₂ той же точки С (судна) по формулам:

sin ϕ 2 = sin ϕ В ⋅ сos Д В + cos ϕ B ⋅ cos Д В ⋅ сos К B-C ,

• tg Δλ 2 = (tg Д B ⋅ sin K B-C )/(cos ϕ B - tg Д B ⋅ sin ϕ B ⋅ cos K B-C ),                            (10)

λ 2 = λ В + Δλ 2 .

Окончательные координаты принимаются как среднее значение, полученное при решении этих двух сферических треугольников

ϕ 0 = ( ϕ 1 + ϕ 2 )/2,     λ 0 = ( λ 1 + λ 2 )/2.                                (11)

В данной схеме вычисления угол пересечения изолиний Θ не играет никакой роли, т.к. исходными данными для вычисления координат являются ортодромический пеленг и расстояние. А эти изолинии пересекаются под прямым углом. Кроме того, по этой же схеме можно определить место судна в любой точке относительно навигационных ориентиров, а также на базе и продолжении базы.

Представляет интерес и другая схема вычислений. Если с ориентиров А и В измерены расстояния Д_А и Д_В до точки С (судна), то можно взять разность расстояний Δ Д = Д_А - Д_В и получим изолинию - сферическую гиперболу. Если взять сумму расстояний Σ Д = Д А + Д В , то изолинией будет софокусный сферический эллипс. Вышеприведенные изолинии пересекаются под прямым углом. Если расстояния Д А и Д_В измерены с погрешностью ± m Д , то разность и сумма расстояний будет иметь погрешность √ 2 m Д , т.е. точность определения места судна будет ниже, чем при использовании первой схемы.

Уравнения сферической гиперболы и софокусного сферического эллипса в прямоугольной сферической системе координат имеют вид tg2Х/a - tg2У/b = 1,                tg2Х/a1 + tg2У/b1 = 1,                        (12)

где Х и У - прямоугольные сферические координаты; а , в - параметры гиперболы; а ₁, в ₁ - параметры эллипса.

Начало сферических прямоугольных координат берется в середине базы А , В . Ось Х - вдоль базы, а У - по нормали из середины базы. Решая систему уравнений (12), находим Х и У . От прямоугольных координат Х и У переходим в географические координаты, используя формулы сферической тригонометрии. Отметим, что данную схему использовать для определения места судна на базе и на продолжении базы не рекомендуется.

3. Заключение

Приведенные выше схемы позволяют контролировать и сравнивать определение места судна, рассчитаннoе аналитически и с помощью электронных карт.

Кроме того, этими схемами можно воспользоваться для проводки судов в узкостях.