Аналитическое представление статистических характеристик случайных процессов с произвольными спектрами

Чувствительность приёмных устройств ограничена их шумами [1]. Это относится и к оптическим квантовым усилителям [2–3], спектры шумов которых отличает свойство узкополосности. Эти спектры разнообразны, и важен поиск аналитических методов расчёта статистических характеристик случайных процессов с произвольными спектрами.

В настоящей работе показано, что статистические характеристики узкополосных стационарных случайных Гауссовых процессов обладают свойством подобия, специфика которого зависит от класса, к которому принадлежит спектр. Выделены и подробно изучены два класса спектров – монохромные, не обязательно одногорбые и бесструктурные, но чья индивидуальность почти не проявляется в характеристиках, и диахромные, типичный вид которых – двугорбый, хотя сюда могут относиться и спектры другого вида. На основе подобия развит метод аналитического представления статистических характеристик процессов с диахромными спектрами через характеристики процессов с монохромными спектрами, описываемые в силу подобия безразмерными универсальными функциями. Обсуждается аппроксимация характеристик для спектров, промежуточных между монохромными и диахромными. Предложена дальнейшая классификация спектров по степени полихромности и аналитическое представление характеристик таких спектров через монохромные универсальные функции. Предложенный метод не доказан строго , но проверен в большом количестве численных расчётов.

Здесь изложены результаты препринтов [4–8] вместе с необходимыми обобщениями.

1. Исходные соотношения

Рассмотрим стационарный случайный узкополосный процесс ξ ( t ) с Гауссовой статистикой и спектральной плотностью G ( ω ) [4]. В силу узкополосности ( ∆ω <<  ω 0 ) представим его как колебание на несущей частоте ω ₀ со случайной комплексной огибающей A ( t )

ξ ( t ) = A ( t ) e^{i ω 0 t} + к . с . (1)

При изучении процесса (1) необходимо исследовать такие его статистические характеристики [9], как коэффициент корреляции

γ(τ) =

ξ ²( t )

∫ ∞

_{= 0} G ( ω )cos( ωτ )d ω ₌

∫ ∞

₀ G ( ω )d ω

= r ( τ ) cos( ω ₀ τ ) + v ( τ ) sin( ω ₀ τ )

коэффициент корреляции мгновенной интенсивности I ( t ) = ξ ²( t ) (при Гауссовской статистике он равен квадрату (2)),

γ ²( τ ) =

ξ ²( t ) ξ ²( t + τ - ξ ²( t ) ² ξ ⁴( t ) - ξ ²( t ) ²

спектр флуктуаций на выходе квадратичного детектора – фурье-образ (3), состоящий из низкочастотной Г 0 ( ω ) (вблизи нуля частоты) и высокочастотной Г 2 ω ₀( ω ) (вблизи ±2 ω 0 ) частей

Γ ( ω ) = (2 π ) ^{- 1 ∞}γ ²( τ ) e^{i ωτ} d τ=Γ 0 ( ω ) +Γ 2 ω ( ω ); (4) -∞                                 ⁰

корреляционную функцию флуктуаций интенсивно-

сти на выходе «идеального» интегратора»

Φ(τ,τs)=

I τ _s ( t ) I τ _s ( t + τ)) - I τ _s ( t ) ²

2 I τ _s ( t )

= τs-2∫0τs ∫0τs γ2(t′ - t′′ + τ)dt′dt′′ =              (5)

= ∫ _- ^∞ _∞ sinc² ( ωτ _s /2 ) ⋅Γ ( ω ) exp( i ωτ )d ω = =τ _s ^{- 2} ∫ ₀ ^{τ s} ( τ _s - t ) ( γ ²( t +τ ) +γ ²( t -τ ) ) d t .

Угловые скобки в (2–3, 5) означают усреднение по ансамблю реализаций ξ ( t ) (полагаем 〈ξ ( t ) 〉 =0), τ – временной интервал между двумя моментами времени наблюдения процесса, sinc x = sin x / x , I _{τ s} ( t ) – скользящее среднее I ( t ) по промежутку времени τ _s

I τ ( t ) = τ^- s ^{1 τ s} ξ ²( t + t ′ )d t ′ . (6) s 0

В силу узкополосности статистические характеристики (2–5) можно выразить [9] с помощью коэффициента корреляции огибающей A ( t ) (1), а случайный процесс описывать не G ( ω ), а полученной из нее смещением на ω ₀ функцией S ( Ω ) = G ( ω ₀ + Ω ), где Ω = ω – ω ₀, – по-

ложительно определенной, локализованной вблизи Q =0, интегрируемой с квадратом функцией (т.е. имеющей конечные интегралы от нее и от ее квадрата), которую будем далее называть просто спектром процесса,

^(Q ) = 2 nf o ( Q )/ т c , r o (O) = 1.

Для функций (7,10,12), объектов нашего дальнейшего анализа, имеют место соотношения

в

∞

(A(t)AЧt + т)\   f S(Q)e-iQTdQ

Y, ( t ) = -—_;-----г—- = —----------=

0''-'                                    ”

( A ( t ) )         [ S ( Q )d Q

-∞

= r ( t ) + iv ( t ).

р ” ।         |2                  г ” —

Y ₀( t ) d T = 2 т _c ; r ₀( to )d to=n / т _c ;

∞                   ∞

Ф (0, т $ ) > т c / т $ . τ _s →∞

Бесконечные пределы интегрирования оправданы

(7) узкополосностью £ ( t ). Тогда S ( Q ) /

∞

S ( Q )d Q -

-∞

фурье-трансформанта Y o ( t ) и наоборот. Для S ( Q ) нечетных y₀ ( t ) комплексна. Но нам понадобится не Y₀ ( t ), а четная функция | Y ₀( t)| = -^ г ²( т ) + v ²( т ) .

Фурье-образ | y₀ ( t )|² - это Г₀( ю ) (4)

f ” I Yo (т)Г eQTdT   Г S(to)S(Q + to)dto r0(Q) = -          1---------■--------------- . (8)

∞

2If S ( Q )d Q )

-∞

Первые два соотношения (13) следуют из (10-11), а асимптотику Ф(0, T _s) можно получить, вынеся r₀( Q ) из-под интеграла в первом равенстве (10) при T _s > ™ [3] или применив к этому равенству разложение функции sinc( x ) по методу Виллиса [10].

Из (13) видно, что (11) определяет характерные временные и частотные масштабы (7,10,12). Однако роль (11) куда более существенна, чем масштаб. Определение T _c (11) наиболее адекватно природе рассматриваемых процессов. В численных экспериментах [4-8] было показано существование таких классов спектров S ( Q ), что для пары случайных процессов со

Функция Г₀( Q ), как и | y₀ ( t )|, чётная. Высокочастотную часть (4) рассматривать не будем.

Когда t_s << 1 / to o (У >  0), то в (6) I _{I s} = ^ ²( t ) и (5) переходит в коэффициент корреляции (3). С ростом т $ при данном т происходит быстрое (за время = 1 / to o ) падение Ф( т , T _s) от у 2 ( т ) до | y₀ ( t )|²/2 (при т = 0 - от 1 до 1/2) с последующим плавным изменением в масштабе времён T _s, т >> 1 / to o . Тогда Ф( т , T _s) (5) приближенно равна [4, 9]

Ф ( т , т $ ) = f sinc² ( Qt $ 1 2) Г ₀ ( Q ) exp( i QT )d Q = _{т (}                                             . (9)

= 0,5 т - ² J O * ( t $ - 1 ) (| Y o ( t + t )| ² + 1 Y o ( t - t )| ² ) d t

Замена Г( to ) в (5) на Г₀( Q ) в (9) означает отбрасывание Г_2wo( to ) (4) в силу sinc( to ₀ T _s/2)<< 1. А замена Y ( t )² в (5) на | y₀ ( t )|²/ 2 в (9) - пренебрежение быстро

спектрами из одного класса отношение их T _c есть коэффициент приближённого подобия одноимённых функций (7,10,12). То есть, если и аргументы (7,10,12) нормировать на (11), то полученные функции при различных S ( Q ) мало отличны друг от друга и с хорошей точностью описываются универсальными функциями, аналитические представления которых можно получить (и не одним способом), рассчитав (7,10,12) для некоторых S ( Q ).

Нормируем временные аргументы (7,10) на (11), вводя £ = т / T _c и п = т / T _c, а частотный аргумент в (12) и S ( Q ) - на обратную величину, вводя % = Qt _c . Саму S ( Q ) тоже нормируем. Тогда вместо (7,10,12) и S ( Q ) получим безразмерные по обеим осям функции

S ™( х ) = 2 S ( х / т c )/ J -” S ( х / т c ) d х ; (14)

осциллирующими и затухающими членами при T _s, т >> 1 / to o . Полагая далее T _s, т >> 1 / to o , имеем (5) в виде (9) с Ф( т , 0) = | Y₀ ( t )|² /2 и Ф( 0 ,0) = 1/2. При т = 0 (9) дает дисперсию флуктуаций (6)

Ф (0, T _s) = Г sinc² ( Qt _s /2) • Г ₀( Q )d Q =

^{J -}” _т                                 .           (10)

^T/ jj^T. ^- t )|Yo ⁽ t ^)2d t

| Y 0n©| = | Y o ( ^t _c )| = | г ( ^т _с) + iv ( ^т _с )|;             (15 a )

Г 0^п ( х ) = 2 пГ 0 ( х / T c )/ T c ;                         (15 b )

Ф ^8П( П ) = Ф (0, nT _c).

(15 c )

Из (9-10) следует, что (9) выражается через (10)

^{Ф ( т} , ^т $ ) = ^; ^{2 т} $

' ^{( т} $ + ^{т )2 ф (0, т} $ +^{т ) - 2 т} 2 ^{ф (0, т )} +" _v+ ( т $ - т )² Ф (0, т $ -т )              ,

Функции (7,10) безразмерны     Y o (O) = 1,

Все функции (15) чётные. Назовем (14) собственно нормированной функцией, т.к. она получается нормировкой S ( Q ) по осям на величины, вычисляемые через S ( Q ). Индекс «sn» у функций (15) означает, что и они нормированы с помощью T _c, получаемого в (11) из того же спектра S ( Q ). Из (14) следует

”                  ”           2

J -” S ™( хМ = 2, J -” ( S ^8П ( х ) ) d х = 4/ п .         (16)

Ф( 0 ,0) = 1/2), а (8) имеет размерность времени. С ее помощью введем время корреляции процесса (1)

т c = 2 nr o (O) = J _o ”| Y o ( T )|²d T =

= n J ” S ²( Q )d Q / ( J” S ( Q )d Q )

совпадающее с одним из его определений в [9]. Нормированная на (11) функция (8) также безразмерна

Если S ^sn( х ) подставить в (11), то получится 1 и повторная процедура нормировки (14) с учетом (16) не изменит S ^sn( х ). То же будет, если для S ( Q ) уже выполнено (16). Т.е. (16) - необходимые и достаточные условия собственно нормированности S ( Q ).

В новых переменных (7,10,12) примут вид

|yn ( < ) = (1/2) J -” S (/. e- i ^х ,

(17 a )

Γ ^{ɶ s} 0 ⁿ( χ ) = (1/2) ∫ _- ∞ _∞ γ ^s 0 ⁿ( ξ ) I ² e^{i χξ} d ξ =

^-∞                       ,            (17 b )

= ( π /4) ^∞ S ^sn ( x ) S ^sn ( x + χ )d x

-∞

Φ ^sn ( η ) = (1/2 π ) ^∞ Γ ^{ɶ s} 0 ⁿ( χ ) sinc²( ηχ /2)d χ _η ^{- ∞}             ₂               .        (17 c )

= η^{- 2} ∫ ₀ ( η -ξ ) I γ ^s 0 ⁿ( ξ ) I ²d ξ

Далее изучим совпадение одноимённых характеристик (17) для моно- и диахромных спектров (14), выделенных предложенными ниже критериями.

2. Монохромные спектры

В расчётах (17) для разных S ^sn( χ ) (14): четных, нечетных, одногорбых и с экстремумами – выделились спектры, названные нами монохромными. Их выделяют два критерия протяженности по оси абсцисс.

Первый ограничивает размер «ядра» спектра (14), определяемого шириной центральной его части, содержащей 50 % всей площади под кривой S ^sn( χ ) при условии равенства площадей оставшихся частей, т.е.

^χleft S ^sn ( χ )d χ : ^χright S ^sn ( χ )d χ : ^∞ S ^sn ( χ )d χ= 1:2:1, n -co                      J у                          v у .

χ left                                  χ right

s 0,5 ⁼ χ right ^- χ left ^≤ π / 2.

Табл. 1. Выполнение критериев (18 – 19) для некоторых спектров S ^sn( χ )

Форма собственно нормированного спектра S s n ( χ ) и его обозначение		s 0,5 / (π / 2)	s 0,9 / π
Гауссова S G ( χ ) = (2V2/ π ) ⋅ exp( - 2 χ 2 / π )		0,76	0,925
Параболическая S p ( χ ) = (2,5/ π )(1 - (5 χ /3 π )2 ), χ ≤ 0,6 π		0,83	0,875
Экспоненциальная симметричная S e ( χ ) = (4/ π ) ⋅ exp( - 4 1 χ / π )		0,69	1,15
Пол-экспоненциальная S he ( χ ) = (4/ π ) ⋅ exp( - 2 χ / π ), χ ≥ 0 [7]		1,1	1,51
Прямоугольная S r ( χ ) = 2/ π , 1 χ ≤π /2		1	0,9
Треугольная равнобедренная S t ( χ ) = (3/ π )(1 - 1,5 1 χ / π ), 1 χ ≤ 2 π /3		0,78	0,91
Прямоугольно-треугольная S rt ( χ ) = (3/ π )(1 - 3 χ / 4 π ), 0 ≤ χ ≤ 4 π /3 [7]		0,98	1
Лоренцева симметричная S L ( χ ) = (4/ π )/(1 + 4 χ 2)		0,64	2,01
Пол-лоренцева S hL( χ ) = (4/ π )/(1 +χ 2), χ ≥ 0	[7]	1,27	4,02
Состоящая из суммы трех экспонент S 3e ( χ ) [7]	штрихпунктирная линия 1 на рис.1	0,75	1,17
	штрихпунктирная линия 2 на рис.1	0,95	0,99

Для спектров табл. 1 почти все характеристики (17) считаются аналитически, что облегчает анализ их свойств для произвольных монохромных спектров. Для симметричных S ^sn(χ) табл.1 функции (17) даны в табл. 2, остальные приведены в [6–7]. В табл. 2 фигурируют специальные функции: si x = ∫ ₀ ^x sinc t d t , cin x = ∫ ₀ ^x [ (1 - cos t )/ t ] d t , erf x = (2/ Vπ ) ∫ ₀^xexp( - t ²) d t – интегральные синус, косинус и интеграл ошибок.

На рис. 1 показаны семь монохромных спектров из табл. 1 (5 четных, используемых далее, и 2 несимметричных, состоящих из трех экспонент, с несколькими экстремумами). Отвечающие им одноимённые функции (17) близки друг к другу.

Степень совпадения функций (17 a – c ) монохромных спектров разная. Так, | γ ^s₀ⁿ ( ξ )| близки у главного

Максимальное значение (18) для S _0,5 точно равно полуширине S ^sn( χ ) прямоугольной формы. Исследования показали необходимость (18) для отнесения спектра к классу монохромных.

Второй критерий схожим образом ограничивает размер основной части спектра (14), где теперь содержится 90 % площади под кривой S ^sn( χ ), т.е.

′′∞ leftSsn(χ)dχ: rightSsn(χ)dχ:     Ssn(χ)dχ=1:18:1, v - co                         * У, r                          * У * V

χleft                                χright s0,9 = χ′right- χl′eft ≤π.

Критерий (19) выступает как достаточное условие монохромности спектра, и его нередко можно ослабить до s 0,9 ≤ (1,25 ÷ 1,5) π . В (18– 19) не фигурируют особенности форм спектров.

Критерии (18 – 19) независимы, т.е. спектры могут удовлетворять или не удовлетворив обоим или только одному из них. Выполнение (18 – 19) обсуждалось в [4,7 –8] для многих спектров: симметричных и несимметричных одногорбых и состоящих из отдельных частей. Часть этих данных приведена в табл. 1.

максимума при | ξ | ≤ π /2, где | γ ^s₀ⁿ( ξ )| ² ≥ 0,1 , «хвосты» же сильно разнятся. Несмотря на близость I γ ^s₀ⁿ ( ξ )I, ненулевые четные члены их разложения в ряд Тейлора в точке ξ =0 не совпадают даже для четных S ^sn( χ ) табл. 1 [5]. Характеристики Γ ₀ ^sn ( χ ) и Ф ^sn ( η ) выражаются (17 b – c ) через I γ ^s₀ⁿ ( ξ ) I . Функции Γ ^{ɶ s}₀ⁿ ( χ ) группируются в узкую полосу. Лучшее совпадение наблюдается у функций Ф ^sn ( η ). Для оценки часто незаметных для глаза отличий Ф ^sn ( η ) в [6] была использована теория нечетких множеств. Отличия Ф ^sn оказались порядка единиц процентов во всей области определения. И при этом у Ф ^sn ( η ) из табл. 2 не совпадают как ненулевые члены разложения в ряд Тейлора при η =0, так и следующие за первым (13) члены асимптотического разложения при η → ∞ [5].

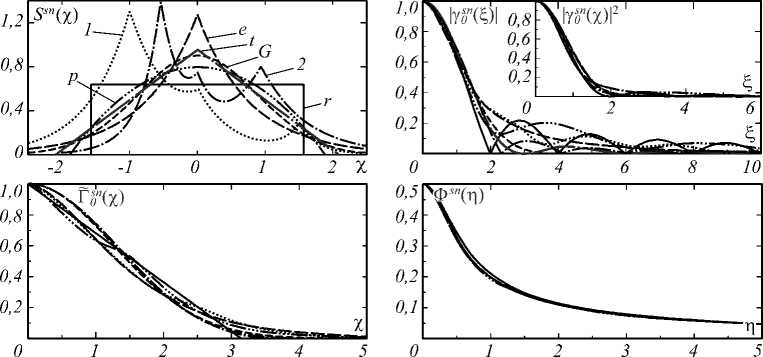
Рис. 1. Графики монохромных S ^sn( χ ) (5 четных, 2 состоящих из трех экспонент) и функций (17) для них. Соответствие вида линий спектру показано буквами, совпадающими с индексам у S ^sn( χ ) в табл. 1-2

Табл.2. Характеристики γ ^s₀ⁿ ( ξ ) , Γ ^{ɶ s}₀ⁿ ( χ ) и Φ ^sn ( η ) для некоторых собственно нормированных спектров S ^sn( χ )

Спектр	γ s 0 n( ξ )			Γ ɶ s 0 n( χ )			Φ sn( η )
S G ( χ )	γ 0 G = e -ξ 2 π /8			ɶ G      -χ 2 / π 0 = e			Φ G = (2/ πη 2) ( ( πη /2) ⋅ erf( πη /2) + e -η 2 π /4 - 1 )
S e ( χ )	γ e 0 = 1/(1 + ( πξ /4)2)			Γ ɶ e 0 = (1 + 4 χ / π ) e - 4 χ / π			Φ e = 2 arctg( πη / 4) / ( πη )
S p ( χ )	γ 0 p =	sin z - z cos z		Γ ɶ 0 p = (1 - z )3(1 + 3 z + z 2),			6 + 5 z 2 - 3,75 z 4 + z ( z 2 - 6)sin z + + ( z 4 - 2 z 2 - 6) cos z + z 5 si( z ) Φ p =               (15 z 6 /36)             , z = 1, 2 πη
		z 3 / z = 3 π ξ	3 /5	z = 5	χ	6 π ≤ 1
S t ( χ )	γ 0 t = sinc2( πξ /3)			[1 -3Z 2 t z 1 0    1      4 [ (2 - z z = 1,5 χ		(2 - z ),0 ≤ z ≤ 1 )3/4,1 < z ≤ 2 / π	Φ t = z	( -1 - 2 cos z + 2 sinc z + ^ (1 - cos z )l               _              1 + (+(1/4)sinc2( z /2)    J + z ( 2si(2 z ) - si( z ) ) - 3 ( cin(2 z ) - cin( z ) )
								(3 z 2 /4) = 2πη /3	,
S r ( χ )	γ 0 r	= sinc( πξ /2)		Γ 0 r = (1 -	χ	/ π ), χ ≤ π	Φ r = 2( - 2sin2( πη /2) + πη⋅ si( πη ) - cin( πη )) /( πη )2
S L ( χ )	γ 0 L = e -ξ /2			Γ ɶ 0 L = 1/ ( 1 +χ 2 )			Φ L = ( η- 1 + e -η )/ η

Совпадение Γs0n (χ) и Фsn(η), выражаемых через γs0n (ξ) – фурье-образ монохромных Фsn(η), означает, что вид (17b-c) определяется фурье-компонентами Фsn(η)с γs0n (ξ) ≥ 0,3 , где фурье-образ Фsn(η) (17a) монотонен. Т.е. в монохромных спектрах нет разнесённых по частоте компонент, коррелирующих друг с другом и дающих заметные дополнительные максимумы в коэффициенте корреляции, почему спектры и названы монохромными. Случайные процессы с этими спектрами тоже будем называть монохромными.

Учитывая совпадение одноимённых характеристик (17 a - c ) случайных процессов с монохромными спектрами, приравняем их безразмерным универсальным функциям U γ ( ξ ), U _Г( χ ) и U _Ф( η ), в качестве аналитического представления которых можно использовать, например, функции из табл. 2. Для U γ ( ξ ) возьмем три представления – γ ₀^G( ξ ) , γ ^e₀ ( ξ ) и γ ₀^t ( ξ ) :

U _γ ( ξ ) ≈ e ^{-πξ 2 /8} ≈ ( 1 + ( πξ /4)² ) ^{- 1} ≈ sinc² ( πξ /3 ) . (20)

Функция | γ ^s₀ⁿ( ξ )| , в отличие от γ ^s₀ⁿ( ξ ) , не зависит от положения нуля χ в S ^sn( χ ). Поэтому не зависят и остальные функции (17). Если у несимметричного S ^sn( χ ) взять четную часть S _ev ( χ ), то, согласно (20), Re γ ^s₀ⁿ ( ξ ) ≈ U _γ ( ξ / ρ ) , где ρ – параметр симметрии S ^sn( χ ), равный доле интеграла от S_e ² _v ( χ ) в интеграле от ( S ^sn( χ ))² и зависящий от положения нуля χ . В [7] показано, что при любом выборе этого положения | γ ^s₀ⁿ( ξ )| близок именно U γ ( ξ ), а не U γ ( ξ / ρ ).

Как представления U _Г( χ ) удобно взять из табл. 2 почти совпадающие Γ ^ɶ ₀^G( χ ) , Γ ^ɶ ₀^p( χ ) , Γ ^ɶ ₀^t ( χ ) ; пригодятся далее и несколько отличные от них Γ ^e₀ ( χ ) и Γ ₀^r ( χ ) :

U Γ ( χ ) ≈Γ 0 ^G( χ ) ≈Γ ^p 0 ( χ ) ≈Γ 0 ^t( χ ) ≈Γ ^e 0 ( χ ) ≈Γ ^r 0 ( χ ) . (21)

Для U Ф ( η ) подойдет любая из первых пяти почти совпадающих функций табл. 2, но из-за громоздкости формул трех последних удобно взять Ф G ( η ), Ф e ( η ):

U Φ ( η ) ≈Φ e ( η ) ≈Φ G ( η ). (22)

∞∞

J 5 i ( x )d x = 2 X ; J 5 2 ( x )d X = 2(1 -X ),0 < X <  1, (25)

-∞                 -∞

Найденное в [5] приближение Ф G ( η ) в виде рациональной дроби тоже подходит как U Ф ( η ):

U ( _η ) _≈     24(11 - 3 π ) + 16 πη+ 3 π ² η ²

^{Φ η}    48(11 - 3 π ) + 32 πη + 22 πη ² + 3 π ² η ³ .

При нарушении критериев (18– 19) для одногорбых спектров типа S L , S hL , S he (табл. 1) подобие функций (17) всё же имеет место, но с меньшей точностью, и сохраняется характерный вид (17) [7]. Для спектров же из отдельных частей (двух-, трехгорбые и т.д.), содержащих более 5 % площади под кривой S ^sn( χ ), это уже не так: здесь при нарушении (18– 19), как показано далее, вид (17 a – c ) даже качественно отличен от (20 – 23). Для одногорбых спектров выполнение (19) обычно влечет и (18). Но в общем случае для монохромности (19) недостаточно. К спектрам, у которых выполнено (19), а (18) нет, относятся, например, двугорбые спектры с резким спадом по краям и в центре (см. рис. 5 и примеры в [8]): они не монохромны и для них (17 a – c ) качественно отличны от (20–23).

Критерии (18 – 19) выведены из многих примеров. Возможно, можно брать в них интегралы от ( S ^sn( χ ))². В сделанных расчётах это не дало отличий в отборе спектров, для которых хороши приближения (20 – 23).

Если (18– 19) выполнены, то (7, 10, 12) определяются лишь временем корреляции τ c (11). И наоборот, в случае монохромных спектров τ c – вся информация, извлекаемая о спектре из функций (7, 10, 12). Структура спектра не выявляется.

3. Диахромные спектры

Из случайных узкополосных процессов с немонохромными спектрами выделим класс процессов и отвечающих им спектров, названных нами диахром-ными [8]. Их можно представить как совокупность двух монохромных процессов на различных несущих частотах, что отражено наличием в спектре двух частей

S ^sn( χ ) = S 1 ( χ ) + S 2 ( χ ) .                             (24)

Части S _1,2 в (24) полагаются неперекрывающимися.

К диахромным относятся многие процессы с двугорбыми спектрами, но не все и не только они. Для любой пары характеристик таких процессов тоже имеет место подобие с коэффициентом подобия, равным отношению τ _c (11) процессов. Значит, и здесь (17) представимы безразмерными универсальными функциями. Но в отличие от (20–22), почти не зависящих от формы спектра, теперь эти функции зависят от трех безразмерных параметров спектра: нормированного на τ _c частотного расстояния δ между S ₁( χ ) и S ₁( χ ), и параметров λ , κ , характеризующих «веса» S 1,2 ( χ )и S ₁²_,2( χ ) (см. спектры далее на рис. 4–6):

∞

J 52(x)dX =

-∞

∞

4 κ ; S 2 ²( χ )d χ = 4(1 - κ ),0 ≤ κ ≤ 1. (26) ππ

-∞

Параметры λ и κ можно получить и из ненормированного спектра S ( Ω ) как доли интегралов от S _1,2( Ω ) и S ₁²_,2( Ω ) в интегралах от S ( Ω ) и S ²( Ω ).

Как и монохромные, диахромные спектры тоже выделены критериями. При взаимодействии с приборами процессы с такими спектрами проявляют себя как совокупность разнесённых по частоте на расстояние δ коррелирующих друг с другом двух монохромных процессов. Их вклад определяется λ и κ .

Между параметрами λ , κ , τ c (11) процесса со спектром S ( Ω ) и τ _c1,2 (11) процессов со спектрами S _1,2( Ω ), соответственно, имеется связь

τ _{с 1} = ( κ / λ ²) τ _с ; τ _{с 2} = ((1 -κ )/(1 -λ ²)) τ _c ; τ _с = λ ² τ _{с 1} + (1 - λ )² τ _{с 2}.

Из (27) следует представление S _1,2( χ ) и всего S ^sn( χ ) в (24) через собственно-нормированные формы S ₁^s_,ⁿ₂( χ _1,2 = Ωτ _{с 1,2}) (14) частей S 1,2 ( χ ) спектра (24):

S ^sn( χ ) = ^κ S ₁ ^sn λ

+

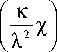
1-κ

1-λ

S sn

Г 1 -к

I (1 -X )²

X I .      (28)

Чтобы процесс был диахромным необходимо, чтобы в (28) его собственно нормированные части S ₁^s_,ⁿ₂( χ _1,2) были монохромны, т.е. удовлетворяли (18– 19) по переменным χ _1,2, а S 1,2 ( χ ) в (24) – соразмерны, что сводится к ограничениям на λ и κ [6, 8]

X ²/ к< 1;(1 -X )²/(1 -к ) < 1 ^X ² <к< 2 X-X ². (29)

Условие (29) взято по максимуму из полученных в расчетах ограничений для разных видов S 1,2 . Поэтому оно достаточно, но не всегда необходимо: и вне (29) часто выполняются выведенные далее соотношения. Для S _1,2( χ ) в (24) (29) обеспечивает выполнение (18– 19) еще и по координате χ . На δ (его смысл обсуждается ниже) накладывается ограничение

δ ≥ (0,5 - 1) πσ (30)

из условия отсутствия пересечения в спектрах с S 1,2 ( χ ) прямоугольной и треугольной форм [8]. Здесь

σ=λ ²/ κ+ (1 -λ )²/(1 -κ ) =τ c ( 1/ τ c1 + 1/ τ c2 ) ≥ 1. (31)

Область λ и κ (29) показана на рис. 2.

Зеркальная перестановка S _1,2( χ ) меняет λ , κ на 1 – λ , 1 – κ , но не меняет функций (17). Далее почти везде λ ≥ 1/2.

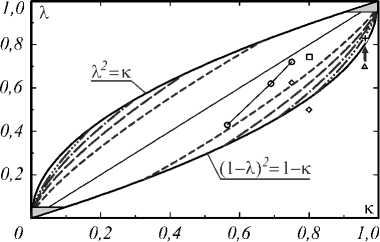
Рис. 2. Область диахромности (29). Внутри нее 1 <  о < 2 . Вдоль диагонали X = к (тонкая сплошная линия) о = 1 . На штриховых линиях λ = κ ± κ (1 - κ )( σ ₀ - 1) значение

² = ² v , © v 2 © cost <К) + ² [ r_x © v 2 © - v , © ^r 2 ©] ^sm( ⁵cJ   и

7 0n , р i зависят от выбора центров S 1, ₂( х ) и 5 .

Если S 1, ₂( х ) симметричны (пусть различны по величине и форме) и 5 - расстояние между их центрами, то S© = 0 и р 1, ₂ = 1. При предложенном далее выборе 5 для любых S 1, ₂( х ) параметры р 1, ₂ близки своим максимумам (когда, по-видимому, р i > 0,8) [7]. Положив в (32) 2© = 0, р 1, ₂=1 и для монохромных S 0П; ( Х 1 ₁₂) заменив |7 сП| и Y sП на U _Y (20), получим

о = о ₀ , а между ними о <  о ₀ . По возрастанию длины штрихов о₀ =1,1; 1,2: 1,3:1,4 . Затемненные куски в углах {0,0} и {1,1} , где X <0,05 и 1- X <0,05 , при любых 5 согласно (19) отвечают монохромному спектру. Их надо исключить из области диахромности. Точки разного вида соответствуют спектрам на следующих рисунках

IYsn (d2 = X2U2 f1 + (1 - X)2U2 f(1 X)2 ^ 1 +0            Y ( к J           Y ( 1 -к J

f X2^ 1    f (1 -X)2^1

^{+ 2 X (1 - X )} U _T l----I • U l — ------I ^{cos( 5}^ )

' l к J Yl 1-к J

, (33)

выраженное через универсальные функции процессов

Подставив (28) в (17 a ), получим для | Y 0 ⁿO² [8]

IY?r = X 2 7 51 ^f

κ

+(1 -X)2 Y; IS-SI 1 -к

+

с монохромными спектрами и удовлетворяющее граничному условию | Y 0 ⁿ(0)| = 1. Приближение (33) -искомое аналитическое представление |Y 0 ⁿ( ^ ) и под-

+2X(1-X)Ynl      IYs021           Icos(5^) + S(^)I KP1 J ( (1-K)p2 J

, (32)

где 5 - расстояние между произвольными (пока) центрами S 1, ₂( Х ); |Уи|, Y s; - функции (17 a ) для спектров S ™( X i ) и их четных частей при отсчете х от упомянутых центров ( 7 0" действительны; р i - параметры симметрии S ⁵"( x i )). Выраженная через мнимые и действительные части (17 а ) функция

ходит для всех рассмотренных диахромных спектров.

Для вывода аналитического представления Г 0^п ( х ) подставим в (17 b ) |Y 0 ⁿ( ^ )| в виде (33), используя разные U ₇ (20). Два первых слагаемых Г 0^п ( х ) при любых S⁵" точно равны их Г 0П . Для монохромных S™ заменим их на U Г (21). Третье слагаемое в Г 0^п ( х ) выражается через (21), если в третьем слагаемом (33) U _Y ~ Y G ~ 7 0 . Так, при U _Y = Y 0 , как показано в [8],

^*

г 0^п ( х ) =

к- Uг(кх / X2) + (1 -к) • Uг( (1 -к)х/(1 -X)2) + 2X(1 -X) [ Uг(2(х-5)/о) + Uг(2(х + 5)/о)] / о1 + 4X(1 -X) • Uг(25/о) / о

. (34)

Знаменатель (34) нужен, чтобы Г 0^п (0) = 1. Если U _г = Г 0 , то U _Г( х >2 5 / о ) = 0 и при х = 0 в (34) квадратная скобка равна нулю, а знаменатель - единице. Для других представлений (21) U _Г(2 5 / о ) ^ 0, и в знаменатель (34) надо ввести второе слагаемое.

Получим Ф^0П( п ), подставив (34) в (17 c ). Два первых слагаемых (34) интегрируются точно при любых S 1,2 . А третье выразится через U _Ф = Ф_г при U _г =Г 0 и единице в знаменателе. Полагая все U _Ф (22-23) равными, для Ф^0П( п ) диахромных процессов имеем

Ф ^0П( П ) = X ² U ф ( X ² n / к ) + (1 -X )² U ф ( (1 -X )² П /(1 -к ) ) +

, (35)

+X(1 -X){(1+25/(по)) Uф(п(о/2+5/п)) + (1-25/(по)) Uф(п(о/2-5/п))-2(25/по) Uф(8q/п)} удовлетворяющее начальному условию Ф0П(О) =1/2.

Формулы (33-35) и есть аналитические представления универсальных функций (17) диахромных случайных процессов. Они получены не для конкретного спектра, а из подобия характеристик монохромных процессов и использования разных представлений описывающих их универсальных функций. Так, (33) получен из (17a) в предположении симметричности и монохромности S 1,2(х); (34) - из (17b, 33) при подста новке в (33) UY = Y0; (35) - из (17c, 34) при подстановке в (34) Uг = Г0. Функции (33-35) четные.

В [6, 8] показано, что 5 в (33-35) есть расстояние между точками деления интегралов от S 1,2(х) пополам (для симметричных S1,2 - между их центрами):

5 = Х С ² ’ -

х™о

Х С ¹ ’ : J c S 1 ( X )d X = J _(Ц S 1 ( X )d X ;

1;              Xc

х(2’

J0= S2(X)dX = Jx,2’S2(X)dX, где χ =0 – точка деления спектра (24) на S1,2(χ). В [8] для S1,2(χ) треугольной и экспоненциальной неравнобедренных форм и некоторых других диахромных спектров вместо (36) опробовался еще один параметр, определяемый аналогично (36), но с S12,2 (χ) под интегралами. При δ из (36) совпадение точных функций (17) с (33–35) оказалось чуть лучше. Поэтому далее будем полагать выбор δ согласно (36).

Погрешности приближений (33–35) для функций (17) диахромных спектров обусловлены подстановками Σ ( ξ ) =0, ρ _1,2 = 1 при переходе от (32) к (33) для несимметричных S _1,2( χ ) и малыми отличиями разных представлений (20–23) для U _γ , U _Г и U _Ф, меняемых при выводе (33–35).

Отличия представлений (20–23) влияют и на сами функции (33–35). Расчеты показали, что в пограничных по критериям (29–30) областях λ , κ , δ это влияние может быть заметным, но для диахромных спектров малó. В расчетах в основном для простоты в (33–35) брались U _{γ, Г,Ф} для S _e( χ ) табл. 1, хотя это не лучший выбор, поскольку есть принципиальные ограничения на U γ, Г,Ф в (33–35), т.к. (33–35) должны отвечать равенствам (13), переходящим для (17 a – c ) в ∞∞

∫ γ ^s 0 ⁿ( ξ ) ²d ξ= 2; Γ ^ɶs 0 ⁿ( χ )d χ=π ; Φ ^sn( η ) → 1 . (37) η→∞ η -∞                 -∞

Из первого равенства и (33) следует условие

∞

∫Uγ(λ2ξ/κ)Uγ((1-λ)2ξ/(1-κ))cos(δξ)dξ=0, (38) -∞ не выполнимое, например, для Uγ = γ0G и Uγ = γe0 . Из монохромных спектров табл. 1 (38) выполнимо для Uγ = γr0,γt0,γ0p при δ ≥ πσ; 2πσ /3; 3πσ /5, соответственно [11 – 12], что совпадает с требованием отсутствия перекрытия S1,2(χ) соответствующего вида. Из рис. 1 и табл. 2, следует, что, пожалуй, лучшая функция из этих трех Uγ = γ0t (ξ) . Ее выбор в (33) требует δ ≥ 0,67πσ, что выше нижней границы критерия (30).

Второе равенство в (37) требует равенства единице знаменателя (34) ( U _Г(2 δ / σ ) =0), т.к. интеграл от числителя равен π при любом U _Г. Из табл. 2 видно, что и тут подходят U _Γ = Γ ₀^r ; Γ ^t₀; Γ ₀^p при тех же ограничениях на δ . Третье равенство в (37) требует для (35) ограничения δ ≥ πσ /2.

В функциях (33–35) асимметрия S1,2(χ) не учтена, а влияние ее на точность аппроксимации (17) для ди-ахромных спектров больше, чем для монохромных. В начале координат в (33–35) роль асимметрии S1,2 мала, как и у монохромных спектров, т.к. в первых двух слагаемых в (33–35) сделана лишь замена (17a – c) на (20–23) для монохромных S1s,n2 . Асимметрия влияет (и заметно) на вторичные экстремумы γs0n (ξ) и Γs0n (χ) : их появление обязано перекрёстным интегралам S1 с S2 и отражено в третьих слагаемых (33–34), где вклад асимметрии S1,2 обусловлен и ею самой (параметрами ρ1,2), и взаимной ориентацией S1,2. При выборе центров S1,2 по правилу (36) поправка на ρ1,2 < 1 невелика и в принципе учитываема. А ориентация S1,2 в (33–34) никак не учтена, т.к. отражение S1 или S2 относительно вертикальных осей через их центры не меняет λ, κ, δ, ρi. Точные же γs0n (ξ) и Γɶs0n (χ) при этом могут меняться [4]. На Фsn(η) ориентация S1,2 влияет мало, и (35) хорошо аппроксимирует (17c).

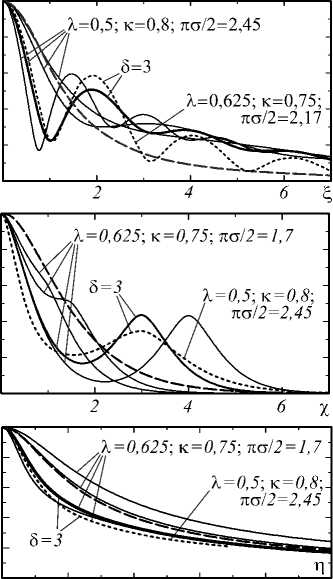
На рис. 3 показано отличие функций (33–35) от (20–22) при двух наборах λ , κ , δ , отвечающих критериям (29–30). Видно, что теперь максимум γ ^s₀ⁿ ( ξ ) при ξ =0 ỳже, чем у монохромных спектров, и есть минимум и второй максимум в области γ ^s₀ⁿ ( ξ ) > 0,3; λ , κ определяют их размеры, δ – положение по оси абсцисс: ξ _min ≈π / δ ; ξ _max ≈ ₂ π / δ . У Γ ^s₀ⁿ ( χ ) первый максимум тоже сужается и при χ max ≈ δ появляется второй. Т.е. для диахромных спектров фурье-образ S ^sn( χ ) уже немонотонен в области γ ^s₀ⁿ ( ξ ) >  0,3 , что означает, что случайный процесс здесь состоит из двух разнесённых по частоте процессов, при определённых значениях τ коррелирующих друг с другом.

lY™@l 0,8 0,6 0.4 0,2

О

ГДх) 0,8 0,6 0,4 0,2

О

Ф™01) 0,4 0,3 0,2 0,1

О 2      4      6      8     10

Рис. 3. Отличие функций (33 – 35) от (20 – 22) для двух наборов λ , κ (ромбики на рис. 2). Сплошные линии – (33 – 35) для одного из наборов при δ = 1; 1,5; 3;4 (с ростом δ кривые вблизи начала координат смещаются справа налево, более толстая линия – δ = 3); пунктирные линии -(33 – 35) при δ = 3 для другого набора λ , κ . Штриховые линии - функции (20–22) монохромного спектра S _e( χ )

В [6, 8] для симметричных и несимметричных двугорбых спектров с симметричными и несимметричными частями (прямоугольной, треугольной, Гауссовой, несимметричной экспоненциальной и др. форм), для спектров, состоящих из трех частей, и одногорбых немонохромных спектров численно было показано, что (33-35) действительно хорошо аппроксимируют (17) диахромных процессов, т.е. являются аналитическими представлениями описывающих их универсальных функций в переменных £ , % , П с параметрами % , к , 5 . Характерный вид функций (33, 34) показан на рис. 4 для двух процессов со спектрами в виде двух неравнобедренных треугольников.

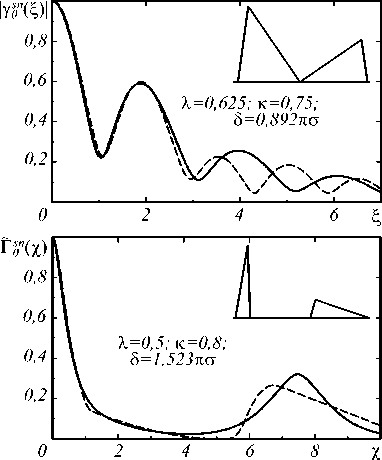
Рис. 4. Сравнение для спектров из двух неравнобедренных треугольников точных | γ ₀ ^sn ( ξ )| и Γ ^ɶ ₀ ^sn ( χ ) (штриховые линии) с (33 – 34) (сплошные линии)

Важный вопрос - аппроксимация функций (17) для промежуточных спектров между моно- и диа-хромными. Есть два варианта перехода диахромного спектра в монохромный: сближение 5 1, ₂( х ) (уменьшение 5 ) до выполнения критериев монохромности (1819) и уменьшение веса одной из 5 1, ₂ ( %, к<< 1 или 1 - %, 1 - к<< 1 ). Рассмотрим оба варианта.

При 5 < п /2 применять (33-35) нельзя, а на границе 8 = ( п /2 ^п ) о надо брать или (33-35), или (20-22), не переходящие друг в друга при формально допустимом 5 <  п / 2, но близкие в этой области. В [8] проанализировано много промежуточных спектров - диа-хромных, почти монохромных, удовлетворяющих (18 -19) или только одному из критериев. Для них точные (17 a - c ) близки и одноимённым функциями (20-22) монохромных спектров, и (33 - 35) диахромных спектров. При этом почти совпадают (22) и (35) для Ф_8П( п ), расхождение же (20-21) и (33-34) для |Y₀ ⁿ( ^ )| и Г 0" ( х ) заметнее. Обычно (33-34) здесь лучше, что показывает рис. 5, хотя точность обоих приближений ((33-34) и (20-21)) обычно хуже, чем (20-21) при выполнении (18-19) и (33-34) при 5 >  по .

В [6] для симметричных ( % = к = 0,5) спектров с 5 1, ₂ прямоугольной, симметричной и асимметричной Гауссовой и экспоненциальной форм получены точные выражения для (17), зависящие от расстояния s между максимумами 5 1, ₂. При больших s они совпадают с (33-35), если s выразить через 5 (36), а при s ^ 0 переходят в (20-22). При этом 5 уменьшается до 5 = п /2, сохраняя это значение вплоть до s = 0.

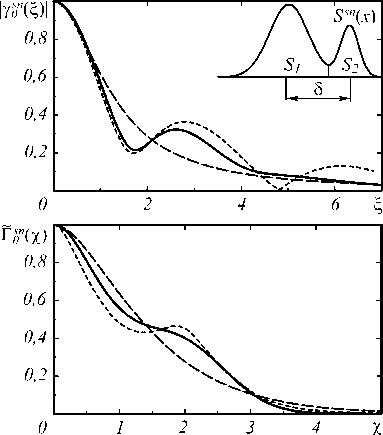
Рис. 5. Функции (17а – б) для почти диахромного спектра из двух симметричных гауссоид (квадратик на рис. 2), близкого по критериям (18 – 19) классу монохромных спектров: s_0,5 = 1,08( π / 2); s_0,9 = π ; λ = 0,743; κ = 0,8;

δ = 0,61 πσ . Сплошные линии – точные функции. Штриховые с длинными штрихами – (20 – 21);

с короткими штрихами – (33 – 34). Функции (22, 35)

и точные Ф^sn( η ) не приведены, т.к. почти сливаются

Переход спектра от диа- к монохромному, когда одна часть спектра много меньше другой, тоже исследован в [8]. Если 5 ₂( х ) = в 5 1 (±( х - 5 )) ( в <<1), т.е. формы 5 1, ₂ одинаковы, то из (33-35) следует (2022). Для произвольных спектров это получается численно. На рис. 2 области этого перехода затемнены.

Набор % , к , 5 может отвечать разным спектрам. Двугорбые спектры 5 ^sп ( х ) (14) при равных % , к , 5 близко локализованы по х , а горбы близки по размерам, т.е. % , к , 5 отражают основные черты таких спектров [6, 8]. На рис. 6 показан пример разных по структуре диахромных 5 ^sn с равными % , к , 5 : два двугорбых (горбы прямоугольной и треугольной неравнобедренной форм) и одногорбый, полученный из спектра пол-лоренцевой формы 5 _hL (табл. 1) отрезанием «хвоста» с площадью 15% от площади под кривой 5 _hL. Оставшаяся часть 5 _hL нормирована по (14) и разделена на 5 1, ₂ в х ₀ = 2,71 (70% и 15% площади под кривой 5 _hL -максимальные монохромные куски 5 _hL). Центры 5 1, ₂ спектров совмещены в точках 0,84 и 3,73 соответственно. Аппроксимация (17) всего спектра 5 _hL обсуждается дальше (рис. 8).

Любой спектр можно по-разному разбить на две части; и % , к , 5 зависят от этого деления.

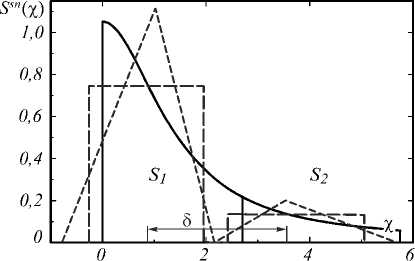
Рис. 6. Три диахромных спектра с λ = 0,823, κ = 0,963 и δ = 0,6 πσ – крестик на рис. 2 (указан стрелкой). Сплошная кривая – обрезанный S_hL( χ ) из табл. 1 (не монохромный: s0,5 = 1,07( π / 2); s_0,9 = 1,38 π ). Штриховые линии – спектры

(30). Для них (слева направо) % возрастает в 1,67 раз (1 - % падает в 2,05 раз), к - в 1,33 раза (1 - к падает в 1,71 раза). А 5 / по возрастает в 1,47 раз ( 5 - в 1,11 раз). Пример рис. 7 показывает, что если % , к , 5 удовлетворяют (29 - 30), то (33 - 35) почти инвариантны к их изменению при смещении точки разбиения спектра в интервале, где диахромность сохраняется.

Нарушение критериев (29-30) увеличивает и расхождение функций (33-35) с (17) и зависимость (3335) от выбора S 1, ₂. Все же и тогда (33-35) применимы как оценочные функции, отражающие основные черты точных функций (17). Нередко (33-35) хорошо аппроксимируют (17) и для недиахромных спектров.

Вероятно, получить универсальные функции характеристик (17) процессов с диахромными спектрами можно и иначе, полагая разбиение S ^п( х ) на S 1, ₂ с перекрытием, допуская 5^ 0 и плавный переход к универсальным функциям монохромных спектров.

4. О возможности обобщения на случай более сложных спектров

Можно ли обобщить предлагаемый метод аналитического представления характеристик (17) случайных процессов на случай процессов с произвольными спектрами? Способ построения (17) диахромных процессов через функции монохромных легко обоб-

щается на «полихромные»: можно так же строить универсальные функции для (17) с три- и более «хромными» спектрами, разбивая спектр на 3 и более неперекрывающиеся монохромные части S i . Эта возможность основана на том, что (17) сводятся к расчету интегралов от всех пар сочетаний частей спектра, самих с собой и перекрестных (для y 0" Й) пары воз

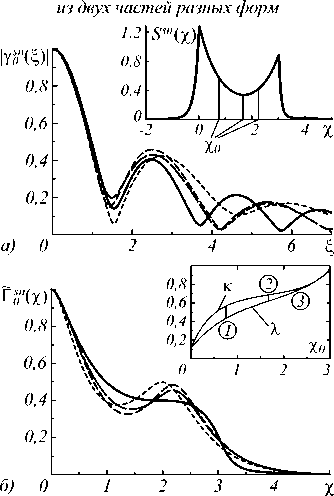
Рис. 7. Точные функции (17a, b) спектра (сплошные линии) и функции (33 – 34) для трех разбиений спектра (кружки на рис. 2, соединенные прямыми), отвечающих условиям (29 – 30): Х ₀ = s/4 ^ { Л К 3 = {0,43; 0,565; 0,6 пс };

Х ₀ = X m™ = 1,67 ~ s/2 ^ {0,62; 0,69; 0,69 пс };

Х _о = 3s /4 ^ {0,72; 0,75; 0,71 пс }, где s = 3 - расстояние между максимумами спектра (штриховые линии; длина штрихов возрастает с увеличением χ ₀). Вверху справа – зависимости λ и κ от χ ₀ в диапазоне от левого максимума спектра до правого

А точные функции (17) не зависят. Поскольку вид (33-35) определяется % , к , 5 (рис. 3) и для диахромных спектров с одинаковыми % , к , 5 имеет место подобие одноимённых функций (17), то во множестве % , к , 5 должны быть подмножества, для которых (33-35) как функции, соответственно, £ , х , П почти инвариантны.

Эта ситуация исследована в [8] при разных диа-хромных спектрах и показана на рис. 7 на примере различного разбиения спектра - суммы двух спектров асимметричной экспоненциальной формы. Для трех точек разбиения % и к удовлетворяют критерию диа-хромности (29), а 5 лежит в пограничной области

никают из-за модуля комплексной функции). Такие приближения характеристик (17) процесса с n-хромным спектром будут иметь вид

2 n С ²£ .

|Т 0" ( ^ > - Z %% ^U , ИI ^U , i , j = 1            V ^ i )

•■v

Г 0 ^п( х ) -

(%²A l

cos( 5 у £ ),

V

κ j

Z % i % j ij - о ij

Г U г

[х+5' о„ / 2 V j 7

+ U г

::‘-.1

n

2 Z ( % i % у / о j )U г (2 5 ij / о у )

i , j = 1

n

Фsn(n) - Z i, j=1

где %i и n

Z % i = 1

i = 1

центров

к

, (40)

λ i λ j

( по ij )²

«веса»

n и Z к i = 1;

i = 1

j Ф ( n Z j !2 п ) -- (2 5 _ц )² U _ф ( n5 _ц I п )

,

интегралов от S i ( х ) и

S ²(X ):

5 ij = - 5 ji - разность координат

S i ( X ) и S i ( х ) (5„ = 0); о _ц =% ²/ к i + % 2 / у

z ij = по .j + 2 5 ij . Функции (39-41) при n = 2 совпадают с (33-35), а при n = 1 - с (20-22). Как и в (33-35), выбор % i , к i и S i ( х ) в (39-41) неоднозначен и часто могут быть приемлемы описания с разными n .

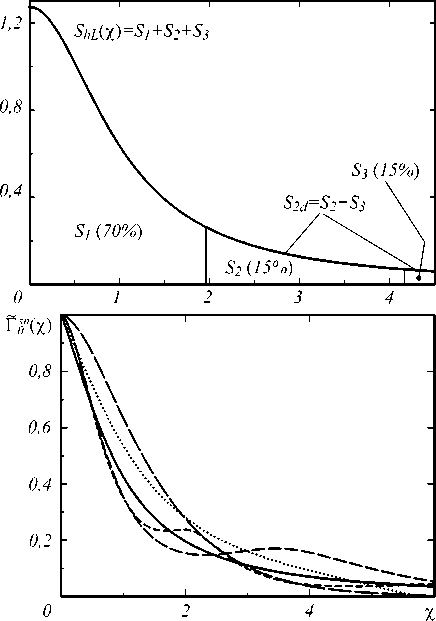
Рис.8. Функции (17) для спектра S _hL( χ ) и их аппроксимации. Сплошные линии – точные функции; с длинными штрихами – (20 – 22) монохромного спектра; со средними штрихами (39 – 41) при n = 2 ( λ = 0,7; κ = 0,96; δ = 0,43 πσ ); с короткими штрихами – (39 – 41) при n = 3 с ( λ 1 = 0,7; ( λ 2,3 = 0,15; κ 1,2,3 = 0,9575; 0,037; 0,0055, δ 12 = 0,6 πσ 12 ; δ 13 = 0,54 πσ 13 ; δ 23 = 0,43 πσ 23 ; пунктир – точные функции обрезанного спектра S_hL( χ ) с рис. 6

Вид полихромного спектра может соответствовать термину n -горбый (иметь n максимумов), а может и нет. По аналогии с диахромными спектрами крите-рием n -хромности спектра можно положить совокупность критериев монохромности (18–19) всех собственно-нормированных частей S_i ^sn ( χ _i ) , условия соразмерности частей λ _i ² / κ _i ≤ 1 и условия на δ _ij ( i ≠ j ), аналогичное (30): | δ _ij | ≥ (0,5– 1) πσ _ij . Из-за условия на | δ _ij |, как и в (33– 35), в (39–41) нет функционального перехода от n -хромности к ( n – 1)-хромности. Многие спектры можно классифицировать, как n -хромный разными способами.

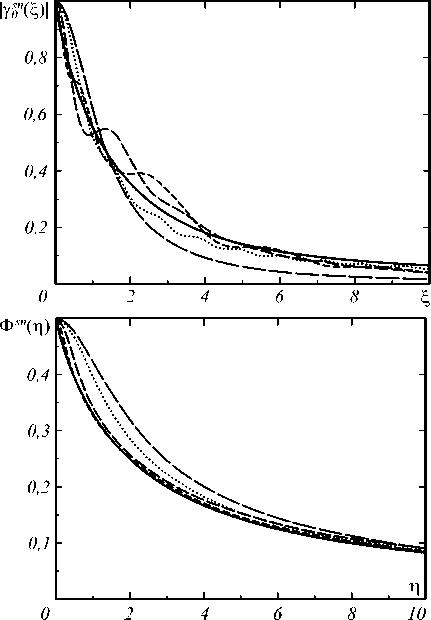
С помощью (39–41) был сделан ряд расчётов для полихромных спектров, состоящих из двух или трех частей прямоугольной или прямоугольно-треугольной форм, считая | δ _ij | по правилу (36) [8]. Почти везде (39–41) при n = 3; 4 дали лучшее приближение, если выполнены вышеупомянутые критерии полихромно-сти. Однако улучшение это невелико, и диахромное приближение уже приемлемо, если за S 1 брать монохромную часть спектра с наибольшим λ 1 . В основном это относится к γ ^s₀ⁿ ( ξ ) и Γ ^{ɶ s}₀ⁿ ( χ ) ; диахромное приближение Ф^sn( η ) во всех случаях было хорошее. А расчёт именно Ф^sn( η ) наиболее труден. Наверное, для n -горбных спектров с большими | δ _ij | различия с диа-хромным приближением заметнее. Для промежуточных спектров проявляется зависимость (39–41) от используемых в них представлений (20–22).

На рис. 8 дан пример аппроксимации (17) с помощью (39–41) для спектра пол-лоренцевой формы S hL (табл. 1). Этот немонохромный спектр не разбиваем на конечное число монохромных кусков, т.к. «хвост» никогда не будет монохромным. Для диахромного приближения (33–35) из S hL отделялась слева наибольшая монохромная часть S 1 с λ 1 =0,7 ( S 2 d – оставшаяся немонохромная часть). И это дало неплохое приближение. Для (39–41) с n =3 к S ₁ из S _{2 d} отделялась вторая наибольшая монохромная часть S 2 с λ 2 = 0,15. И хотя оставшаяся S 3 с λ 3 = 0,15 не удовлетворяет ни одному условию (18– 19), приближения (39–41) оказались хорошими. При λ 1 =0,7 точнее трихромное приближение (39–41) получается именно с λ 2 = 0,15. Если S 3 вообще отрезать от спектра (рис.6), то функции (17) полученного диахромного спектра заметно отличны и от функций (17) для S _hL, и от их трихромного приближения (пунктир на рис. 8).

Заключение

В работе предложен метод, позволяющий с хорошей точностью для узкополосных случайных Гауссовых процессов с различными спектрами получать в аналитическом виде их статистические характеристики – коэффициент корреляции, спектр флуктуаций квадратичного детектирования, корреляционную функцию интенсивности. Он основан на обнаруженном свойстве подобия одноимённых статистических характеристик, что позволяет аппроксимировать их универсальными безразмерными функциями.

Предложенный метод не доказан строго, но проверен множеством расчётов, в которых выявлено подобие характеристик процессов с двумя классами спектров, названных монохромными и диахромными. Установлены критерии принадлежности спектров к этим классам. Для ряда монохромных спектров получены аналитические выражения безразмерных нормированных характеристик, которые можно считать аналитическими представлениями упомянутых универсальных функций. Показано, что универсальные функции диахромных спектров можно выразить через универсальные функции монохромных спектров. Обнаружено, что нередко диахромное приближение удовлетворительно, даже когда критерии диахромности не выполнены.

Для произвольных спектров обсуждается возможность обобщения предложенного метода: дальнейшая классификация спектров по степени полихромности и представление статистических характеристик процессов с такими спектрами через универсальные функции монохромных спектров. На ряде примеров показана перспективность такого обобщения.