Аналитическое решение аномальных диффузионных процессов

В последние годы уравнения с частными производными дробного порядка сыграли важную роль в прикладной математике, физике, технике, экономике и в других областях исследований. Динамические модели растущего числа физических явлений в теории упругости, теории управления, финансов, электромагнетизма, диффузионных процессов и во многих других областях могут быть смоделированы с помощью ДПДУ. В этой работе мы видим, что моделирование процессов аномальной диффузии или дисперсии аналитически разрешено по типу ДПДУ.

Определение 1. Для функции и класса S быстро убывающих тестовых функций на вещественной оси □ . Преобразование Фурье определяется так:

u ( £ ) = F [ u ( x ); ^ ] = J e'u ( x ) dx , % _€q

•

тогда как обратное преобразование Фурье имеет вид

u ( x ) = F "' [ u ( f ); x ] = -¹- Г e- » « ( 5 ) (Ц, 2 n -*              x € □ •

Определение 2. Дробная производная Капуто определяется так:

в^А.    ¹     Ui   n -в - в - 1 d n u ( ^ ) d ^

D_t u ( t )                 ( ^ )                    ,

0 z     Г(n - в) Г           d где

Определение 3. Псевдо-дифференциальный определяется аналитическим продолжением во "  1 <  ^a <  " , " ^^ и a ^ 1 так:

оператор Рисса всем диапазоне

' ^UI‘"_:" = - c [„ D ^ u ( x , 1 ) + Du ( x , 1 ) ] , 51 x

c =----- 7 ----\, ( an )

2 cos II где коэффициент       ^ 2

„_a .    . d" [ I +- ^a u ( x , 1 )"

-. Dx u (x , 1) =-----—= dxn

,

x D a u ( x , 1) = ( - 1) )

dⁿ [ I ) ^-a u ( x , 1) ]

dxn

левые и правые дробные производные Вейля. В уравнениях (5) и (6)

I"-a (в > 0)                                              - через ± (e  ) обозначены дробные интегралы Вейля, определяемые так:

I ’ и ( x ) =   1- Г ( x - ? ) *’^-,u( ? )d ? .

Г ( в ) -”

I ^ и ( x ) =

г в г ? - x ) - -и « «.

Определение 4. Преобразование Лапласа дробной производной Капуто

порядка ⁰ < ^ <  ¹ является

L [ ₀ D e и (1 ) ] = ^"U ( 5 ) - ^ ^{e - 1} и (0), где U^{( 5 )} - преобразование Лапласа ^{и ( 1} ) .

Определение 5. Однопараметрическая функция Миттаг-Леффлера определяется разложением в ряд так:

:      ,y ⁿ

E6 (a) = У —a--- eV J  )=^Г(в" +1)   в > 0.

Пусть ^{и ( x -} y ^{- 1} ) - вещественная, многозначная функция, аргументы в

(x, y) G -п, П X -П, П                          + время переменное.

котором                     - пространство, ^{1 G}

Рассмотрим аномальную диффузию как проблема, которая описано Рисса-

Капуто дробное уравнение в частных производных так:

0 D e и ( x , у , 1 ) =

д ^a u ( x , у , 1 )

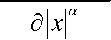
д ^a u ( x , у , 1 ) ^д у ^a ,

⁰ <  в <  1 ^, 0 <  a <  1

,

со следующими начальными и граничными условиями

и ( x , у ,0) = и „ ( x , у )    , I™. ^{и ( x} , ^у , ¹ ) = 0.

,

Следует отметить, что мы понимаем дробные производные пространства и времени в смысле определений Рисса и Капуто, соответственно. Кроме того, мы предполагаем, что решение и функции начальных условий можно разложить в комплексные ряды Фурье.

Предположим, что решение задачи представлено следующими рядами от      от u (x, y. t) =EE knm (t) e"ne";’,         .   !- где

d ^a u ( x , y , t )

Мы вычисляем

5| x “

для этого необходимо вычислить дробные

производные слева и справа по отношению к переменной ^x . Расчет

_D ^a u ( x , v , t )      D “ u ( x , y , t )

- x , y , > и x -    , y , ) выполняется следующим образом:

D> ( x , y , t ) = - оx

Г (1 - a )

u ( ^ , y , t ) ( x - £ Г

d ^

d

8 x

от     от                      ^x         in ^

—L- хУ У k (t) e™m f-e— Г(1 - a) X m^ nm^  £ (x - ^

d ^

2    2               ^imy                                  от    ”                   _   ,    ,

= X X X,' _ x e Г (1 - a )(in) ^a = X X k nm ( t )( in) ^a e i e^,my , n =-от m =-от ^{r (1 a )}                           n =-от m =-от

и

№ ( x , y , t ) = - ( - 1) - d x    dx

1 ^от u ( £ y , t )

Г (1 - a ) J ( x - £ ) ^a

= ( - 1) -dx

Г (1 - a )

n ^

xXX ^k - ( t ) e * J 77^5 n =-от m =-от              x ⁽ ^    ^x )

d ^

CO CO

= zz n =-от m =-от

k nm ( t ) e i^ e i” Г (1 - a )( - in ) ^a Г (1 - a )

CO CO

X Z k nm ( t )( - in) ^a e^inxe^my .

Таким образом, мы получаем

d^a u ( x , y , t ) S| x “

1               CO CO

, X X X k nm ( t)eⁿ x e^my [ ( in ) ^a + ( - in ) ^a ] .

cos — ⁿ =^{-от m} =^-от

I 2 J

d ^a u ( x , y , t )

5| ’ “

1               CO CO

/ X X X knm (texem’ [(im)a + (-im)a ]• cos — n=-от m=-от

I 2 J

Подставив уравнения (11) - (1) в уравнение (9), получим

0 Deknm =--Т^Л ( in )a + (-in )a + (im )a + (-im )a knm '

2 cos

I 2 J

Далее мы берем преобразование Лапласа по времени. Тогда у нас есть

s ^e k ( s ) - s ^{e - 1} k (0) + Ak ( s ) = 0.

A =

где

2 cos

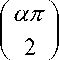
(in )a +(- in )a +(im )a +(- im )a

А' = | n |  + | m|

Рассмотрим основное значение ветвь A для вычислительное цели a и используя ее можем изобретать: Лапласа преобразование.

Уравнение (12) дает

k ( t ) = k (0) E_p ( - At ^e ),

где ^{E p}

- функция Миттаг-Леффлера. Согласно нашим предположениям

и аналогичным функциям, решения ^{u ( x , y , t )} функции начальных условий ^{u 0 ( x , y )} также может быть разложено в ряд Фурье:

∞∞ u0(x,y)= ∑∑u0nm(0)einxeimy,

n=-∞ m=-∞ здесь u0nm (0) - коэффициенты Фурье

ππ u0nm(0) =   1 2      u0(x,y)e-inxe-imydxdy.

( 2 π ) - π - π

С другой стороны, мы берем t = 0 в уравнении (11) и получим knm(0) = u0nm(0) , тогда замкнутая форма аналитического решения задачи получается так:

∞∞

u ( x , y , t ) = ∑∑ u 0 nm (0) E β ( - A ′ t ^β ) e^inxe^imy . n =-∞ m =-∞