Аналитическое решение прогиба дистанционной балки фермы с произвольным количеством панелей

Расчет строительных конструкций производится в большинстве случаев в специализированных пакетах, основанных на методе конечных элементов [1-6]. В такие расчеты включаются все особенности конструкции, тип соединений, иногда переменные сечения элементов, нагрузки сложного вида, неоднородные упругие характеристики материала и т.д. Одновременно с численным подходом к анализу сооружений инженеры пользуются и простыми моделями конструкций, адекватность которых подтверждается практикой. Для ферм, например, соединения стержней моделируются идеальными шарнирами, нагрузки рассматриваются равномерно приложенными к узлам. В этом случае модельное представление дает возможность использовать простые формулы для прогиба, усилий в критических по устойчивости или прочности стержнях. Больше всего в последнее время получено таких формул для регулярных плоских [7-10] и пространственных [11] ферм. Впервые общие вопросы регулярных статически определимых систем были подняты в [12-14]. В точные решения для регулярных систем помимо размеров и нагрузки входят также и число панелей, что делает их удобными как для анализа конструкций, так и для оптимизации на этапе конструирования. В алгоритм вывода большинства расчетных формул регулярных ферм заложен метод индукции по одному или нескольким параметрам. Этим же методом в настоящей работе выводится формула для фермы распорного типа (рис. 1). В [15] эта задача решена при f=h . В [19-23] методом индукции анализируются распорные фермы такого же или близкого типа, но с опорами других конструкций. Задачи о собственных колебаниях плоских ферм с произвольным числом панелей методом индукции в

Kirsanov M., системе компьютерной математики Maple решены в [24-26]. Аналитические решения c многими параметрами могут быть использованы в задачах оптимизации [27-29].

2    Methods

Схема фермы. Определение усилий в стержнях. Верхний пояс, подверженный сжатию от вертикальной нагрузки, составлен из укороченных элементов, что обеспечивает больший запас ее устойчивости. Длина каждой панели 2 a. Панель состоит из двух горизонтальных стержней верхнего пояса, одного стержня нижнего пояса, четырех раскосов и стойки высотой f . Две неподвижные опоры не делают конструкцию статически неопределимой, так как число ее узлов 4 n +4, а число стержней m =8 n +8, но затрудняют определение реакций опор и усилий в стержнях. Обычные три уравнения равновесия конструкции не позволяют определить четыре неизвестные реакции независимым образом. Для этого надо составлять уравнения равновесия всех узлов и решать полученную систему, в которую помимо усилий в стержнях входят и реакции опор.

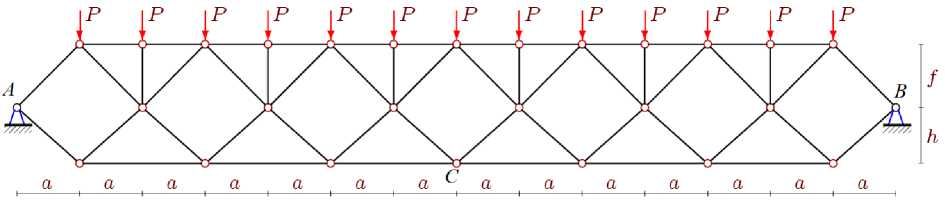
Рис.1. Ферма, n =6/ Fig.1. Truss, n =6

Систему уравнений удобно составлять в программе, написанной на языке Maple и опробованной в различных задачах с фермами [5-10]. Стержни и узлы фермы нумеруются (рис. 2). В программу вводятся координаты узлов и порядок соединения стержней. Приведем фрагмент программы ввода координат:

• >    for i to 2*n+1 do x[i]:=(i-1)*a; y[i]:=h+f;        end:

• >    for i to n+2 do x[i+2*n+1]:=(i-1)*2*a-a; y[i+2*n+1]:=h; end:

• >    for i to n+1 do x[i+3*n+3]:=(i-1)*2*a; y[i+3*n+3]:=0; end:

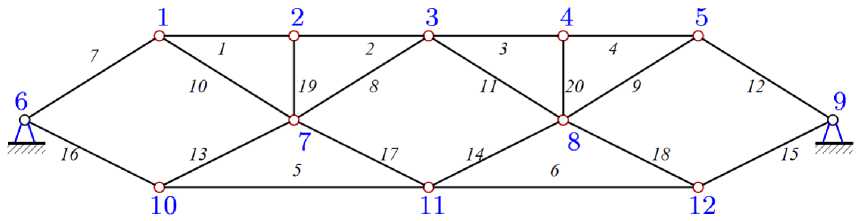
Рис. 2. Номера узлов и стержней фермы, n = 2

Fig. 2. Numbers of truss nodes and rods, n = 2

Структуру соединений стержней фермы определяют векторы Z[i] , привязанные к стержням и содержащие номера их концов. Для стержней верхнего пояса имеем следующие векторы:

• >    for i to 2*n do Z[i]:=[i,i+1]; end:

Для стержней нижнего пояса:

• >    for i to n do

Z[i+2*n]:=[3*n+3+i,i+3*n+4];

Z[i+7*n+4]:=[2*n+2+i,2*i]; od:

Матрица уравнений равновесия заполняется направляющими косинусами усилий.

Система решается в символьном виде методом обратной матрицы, что несколько быстрее в системе Maple, чем использование специальных операторов пакета LinearAlgebra. Все усилия и

Kirsanov M., реакции опор определяются в символьном виде. Схема распределения усилий в стержнях фермы при n=4 показывает, что как и следовало ожидать, нижний пояс фермы растянут (стержни выделены красным цветом), верхний — сжат (синий цвет). Толщина отрезков пропорциональна модулям усилий, числа указывают на значения усилий, отнесенных к силе P.

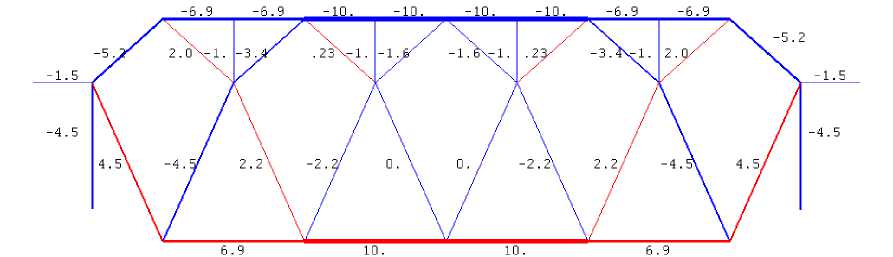
Рис. 3. Распределение усилий в стержнях, n =4, a =6 m, h =5 m, f = 2m

Fig. 3. The distribution of stresses in the bars, n =4, a =6 m, h =5 m, f = 2m

Прогиб. Прогиб вычисляется по формуле Максвелла – Мора m-4 Со/

A = V S j s j l j

" Й EF где EF — жесткость стержней, S – усилие в стержне j фермы от действия приложенной нагрузки, s – усилия от единичной силы, приложенной к узлу C, вертикальное смещение которого разыскивается, l – длина стержня j. Четыре опорные стержня, принятые жесткими, в сумму не входят.

Пробные расчеты в аналитической форме при разных числах панелей показали, что для нечетных n определитель матрицы уравнений равновесия обращается в ноль. Заметим, что за счет погрешности вычислений расчет в численной форме не дает этот результат. Вырождение определителя свидетельствует о мгновенной кинематической изменяемости конструкции. Найдена соответствующая картина распределения возможных скоростей узлов фермы при n =1 (рис. 4). Очевидны соотношения скоростей: v / c = u / h , v '/ g = u I h , где c = V a ² + h ² , g = 7 a ² + f ².

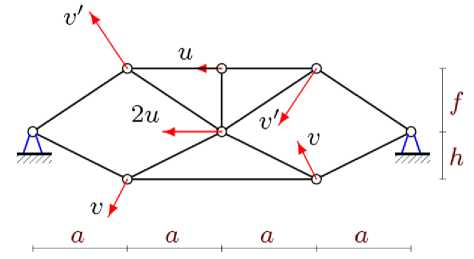
Рис. 4. Схема возможных скоростей, n =1,

Fig. 4. Diagram of possible velocity of nodes, n =1

Аналогичную схему можно получить и для других нечетных значений n . Далее в расчетах примем n =2 k. Для произвольных k решение имеет вид:

A = P ( C 1 a ³ h + C ₂ a ³ f + C ₃ g ³ h + C ₄ c ³ h + C ₅ c ³ f )/( h ( h + f )² EF ) .           (2)

Kirsanov M.,

Коэффициенты C, i = 1,..,5 зависят только от k. Определение этих зависимостей составляет основную трудность задачи.    При получении коэффициента C пришлось рассчитать прогибы 18 ферм. Меньшее число ферм не выявляет общего члена последовательности 48,224,1136,2512,6592,11216,.... Для этой последовательности оператор rgf_findrecur системы

Maple из специализированного пакета genfunc генерирует однородное рекуррентное уравнение девятого порядка:

C k = C i,к - 1 + 4 C к — ₂ - 4 C к — 3 - 6 C к - ₄ + 6 C к — 5 + 4 C i, k — ₆ - 4 C k — ₇ - C k — ₈ + C к — ₉ .

Решение рекуррентного уравнения с начальными данными C ,= 48, ..., C ₁₅ = 6592 дает оператор rsolve:

C ₁ = (20 к ⁴ + 8(5 - ( - 1) ^к ) к ³ + 2(17 - 6( - 1) ^к ) к ² + 2(7 - 5( - 1) ^к ) к - 3( - 1) ^к + 3) / 3.     (3)

Остальные коэффициенты получились проще, число членов соответствующих последовательностей было меньше:

C ₂ = (8 к ³ ( - 1) ^к + 6(2( - 1) ^к - 1) к ² + 2(5( - 1) ^к - 3) к + 3( - 1) ^к - 3) / 3,

C ₃ = 2 к ² + 2(1 - ( - 1) ^к ) к - ( - 1) ^к + 1,                                              (4)

C ₄ = 2 к ² + 2 к ,   C ₅ = 2 к ( - 1) ^к + ( - 1) ^к - 1.

Слагаемые, содержащие множители ( - 1) ^к , показывают что решение зависит от четности числа панелей в половине пролета. Проверка коэффициентов выполнялась сравнением с численным решением при различных k .

3    Results and discussion

Формула (2) с коэффициентами (3), (4) дает решение поставленной задачи. Анализ этого решения составляет отдельный интерес. Как оказывается, полученное решение обладает рядом интересных особенностей, проследить которые удобно на графиках кривых, построенных для безразмерного прогиба А' = AEF /(pL), гдер = P(2n +1) — суммарная нагрузка, a = L /(2n + 2) — длина панели при фиксированном пролете (рис. 5). Прежде всего следует отметить несколько неожиданно сильную, скачкообразную зависимость прогиба от четности числа панелей. Особенно существенны скачки при малом числе k. Далее кривая несколько сглаживается, имея наклонную асимптоту. Средствами Maple получаем угол наклона асимптоты г         f2 - hf + h2

lim А '/ к = ------------- .

k           2 L ( h + f )

Kirsanov M.,

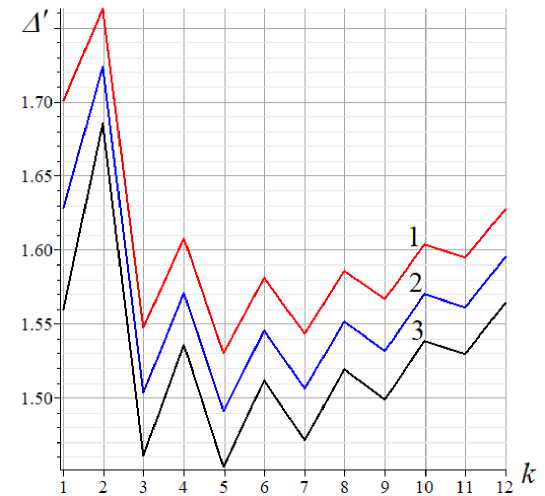
Рис. 5. Зависимость прогиба от числа панелей, h = 3m, L =50 m, 1— h =4.0 m; 2— h =4.1 m; 1— h =4.2 m;

Fig. 5. Deflection dependence on the number of panels, h = 3m, L =50 m,1— h =4.0 m; 2— h =4.1 m; 1— h =4.2 m

Ферма по высоте несимметричная. Можно предполагать, что соотношение высот f и h влияет на прогиб. Примем, например, высоту фермы равной f + h = 10 м. На графике видно, что поведение кривых прогиба в зависимости от f для четных и нечетных значений k принципиально отличается (рис. 6). В первом случае прогиб растет при увеличении f , во втором — падает. Следовательно, для ферм с четным значением k (или, что то же, число панелей n кратно 4) для увеличения жесткости следует брать f < h . Для нечетных k более жесткой будет ферма при f > h. В любом случае, если не стремиться к точному минимальному прогибу, то при любом k лучшее решение будет при f=h , а при f>h прогиб будет больше.

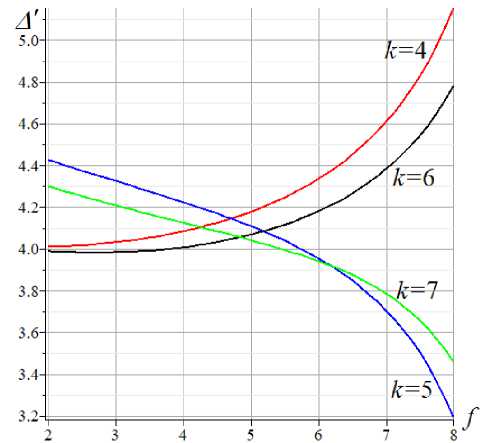
Рис.6. Зависимость прогиба от f при f+h =10 m, L =120 m, Fig. 6. Deflection dependence on f at f+h =10 m, L =120 m

Kirsanov M.,

4    Conclusions

Проведенный анализ позволяет сделать следующие выводы:

• 1.    Распорная схема фермы шпренгельного типа с параллельными поясами и ромбической решеткой допускает точное решение задачи о зависимости прогиба от числа панелей. Формула содержит сравнительно простые коэффициенты полиномиального вида степени не выше четвертой.

• 2.    При нечетном числе панелей ферма обладает свойством мгновенно изменяемого механизма, что не допустимо для ее практического применения. Одновременно это и предостережение для тех, кто готовые решения для одних регулярных конструкций экстраполирует на другие, пусть даже похожие, например, отличающиеся всего на одну панель. Всегда необходима проверка кинематической изменяемости при любом числе панелей.

• 3.    Показано, что на выбор геометрических размеров при поиске оптимальных по жесткости ферм, влияет четность числа панелей в половине пролета.

5    Acknowledgements

This research work was supported by the Academic Excellence Project 5-100 proposed by Moscow Power Engineering Institute, Moscow, Russian Federation.