Аналитическое решение связанной задачи об отыскании поля перемещений чувствительного элемента акселерометра с учетом влияния электростатических сил

Пермский государственный технический университет

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СВЯЗАННОЙ ЗАДАЧИ ОБ ОТЫСКАНИИ ПОЛЯ ПЕРЕМЕЩЕНИЙ ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА

АКСЕЛЕРОМЕТРА С УЧЕТОМ ВЛИЯНИЯ ЭЛЕКТРОСТАТИЧЕСКИХ СИЛ∗

Решается связанная задача о расчете статических перемещений чувствительного элемента микромеханического акселерометра, вызванных действием инерционных сил и сил электростатического взаимодействия. При решении используются упрощенные балочные модели, решение ищется методами сопротивления материалов. Исследуется нелинейный характер основных характеристик датчика. Определяется, с учетом действия кулоновских сил, диапазон возможных измеряемых ускорений.

Цель работы – построение модели микромеханического акселерометра (ММА) и определение на основе этой модели степени влияния электростатических сил, возникающих в конструкции во время ее работы, на статические перемещения чувствительного элемента датчика. Объектом исследования является микромеханический акселерометр, состоящий из внешней пластины, являющейся чувствительным элементом датчика, внутренней пластины, прикреплённой к внешней посредством двух упругих перемычек и системы обкладок конденсаторов, часть которых размещена на чувствительном элементе и является подвижной, а другая часть – на неподвижном корпусе прибора на некотором удалении от чувствительного элемента [1–4]. Схематичное изображение ММА показано на рис. 1.

Рис. 1. Схематичное изображение микромеханического акселерометра

1 – чувствительный элемент ММА (внешняя пластинка),

2 – внутренняя пластинка,

3 – область крепления к неподвижному основанию прибора,

4 – упругие перемычки,

5 – система подвижных обкладок

^∗ Работа выполнена при финансовой поддержке гранта РФФИ (проект № 09-08-99121-р_офи)

Во время работы датчика внешняя пластинка ММА, подвешенная на упругих перемычках, отклоняется под действием переносных сил инерции, вызванных действием приложенного ускорения. Величина отклонения чувствительного элемента определяется посредством измерения емкости конденсаторов, образованных системой подвижных и неподвижных обкладок на чувствительном элементе и основании датчика. Во время измерения емкости на обкладки конденсаторов подается разность потенциалов, приводящая к накоплению на обкладках электрических зарядов, что, в свою очередь, приводит к дополнительному сближению обкладок под действием сил кулоновского взаимодействия.

Связанную задачу о расчете статических перемещений чувствительного элемента микромеханического акселерометра, вызванных действием инерционных сил и сил электростатического взаимодействия, решим аналитически следующим образом. Считаем, что внутренняя и внешняя пластины абсолютно жесткие. Рассмотрим упрощенную модель ММА, состоящую из абсолютно жесткого недеформируемого чувствительного элемента, подвешенного на двух упругих перемычках с известной изгибной жесткостью. В процессе работы датчика происходит деформация только лишь упругого подвеса. На чувствительный элемент акселерометра действуют измеряемые датчиком переносные силы инерции P _a и дополнительные паразитные силы электростатического взаимодействия P _e , возникающие между подвижными обкладками конденсатора переменной емкости. Обозначим результирующую всех внешних сил, действующих на чувствительный элемент, как P :

P = P _a + P .

Упругие перемычки рассматриваются как балки с известными геометрическими параметрами и жесткостными характеристиками. Схематическое изображение упрощенной модели ММА показано на рис. 2, а.

PP l        l       ll a                                  б

Рис. 2. Упрощенная схема модели ММА:

а – схема с чувствительным элементом;

б – упрощенная схема без чувствительного элемента

Так как чувствительный элемент датчика считается недеформируемым, то схему можно еще более упростить (рис.2, б), необходимо лишь дополнительное условие равенства нулю угла поворота в точке соединения балок, обусловленное физическим смыслом задачи - движение чувствительного элемента осуществляется таким образом, что он всегда остается параллельным основанию прибора (подложке):

0| п= 0.

x = 0

Решение задачи, расчетная схема которой представлено на рис. 2, б возможно провести с использованием упрощенных инженерных методов сопротивления материалов, применяемых для исследования напряженно-деформированного состояния упругих балочных конструкций [5]. Отметим, что поставленная задача является статически неопределимой и для ее решения требуется решение уравнений равновесия совместно с геометрическими и физическими соотношениями. Однако, расчетная схема на рис. 3, б является симметричной относительно геометрии конструкции, условий закрепления и приложенных силовых факторов. В данном случае возможно проведение решения лишь для половины конструкции, что позволит еще более упростить расчетную схему и сделает задачу статически определимой. На конце консольной балки будет действовать сосредоточенная сила P 2 и сосредоточенный изгибающий момент M 2 , обеспечивающий равенство нулю угла поворота чувствительного элемента и его параллельность основанию прибора (подложке). Окончательная расчетная схема представлена на рис. 3. В дальнейшем, при составлении всех уравнений будем считать, что начало координат используемой системы отсчета связано с левым консольным краем балки на рассматриваемой расчетной схеме.

M

P

l

h

z

■>

b

Рис. 3. Окончательная расчетная схема ММА

Определим статические прогибы упругих перемычек. Для этого выполним последовательное интегрирование уравнения моментов с последующим вычислением постоянных интегрирования исходя из граничных условий. Уравнение моментов для заданных условий закрепления и силовых факторов в описанной выше системе отсчета примет вид

M (x ) —

Выполним интегрирование уравнения углов поворота балки от координаты:

MP

— x .

моментов для получения зависимости

0( x ) = ej J M (x) dx,

1 ( M   P 2 ) _

0( x) —        x--x +0 ,

' ' EJ ( 2     4 J ⁰

где 0 - угол поворота балки, 00 - постоянная интегрирования, имеющая физический смысл угла поворота в точке с координатой x — 0, E - модуль Юнга, J - момент инерции поперечного сечения балки, выражающийся в виде bh3

= 12 , где b и h – соответственно ширина и высота поперечного сечения упругого подвеса.

Постоянную интегрирования 0 ₀ определим из граничных условий. Так как чувствительный элемент датчика всегда параллелен основанию, совершает только поступательное движение и не поворачивается, то в точке x — 0 (в данном случае - это точка крепления упругой перемычки к чувствительному элементу датчика) угол поворота балки должен быть равен нулю. То есть

⁰I x — 0 — ⁰.

M ■ 0 - P ■ 0² I+ 0_O = 0, 2      4 J ⁰

следовательно,

0 0 = 0.

Также из граничных условий можно определить величину момента M , возникающего в сечении в точке x = 0. Для рассматриваемой расчетной схемы при консольном закреплении в правой части в точке x = l углы поворота должны быть равны нулю.

0| = 0,

I x = l

M_l 2

р Л   М Р 1

Pl ² I = 0, Ml - Pl ² = 0,

4 J      24

M = P 2.

Таким образом, уравнение для углов поворота принимает вид

P ■ lP

.

---xx

Для определения прогибов балки проинтегрируем выражение для углов поворота: y ( x ) = J 0 ( x ) dx ,

( A    1 ( P ■ l 2 P з)

y (x ) =          xx + y,,

' ⁷ EJ ( 8       12 J ⁰

где y0 – постоянная интегрирования, имеющая физический смысл прогиба балки в точке x = 0 . Постоянная y0 может быть определена из граничных условий. В области жесткой заделки прогибы балки должны равняться нулю, то есть yx=l = 0,

y (l ) = — f P-1 l2 - Pl31 + y0 = 0, v 1 EJ I 8      12 J 0

У 0 =

Pl ³

24 EJ

.

В решаемой задаче величина y ₀ имеет первоочередное значение, так как она соответствует прогибу балки в точке x = 0, что, в свою очередь, исходя из постановки задачи и рассматриваемой расчетной схемы, численно равно перемещению чувствительного элемента микроакселерометра под действием приложенной к нему силы P любой природы.

Рассмотрим более подробно силы, действующие на чувствительный элемент микромеханического акселерометра. На чувствительный элемент датчика действует переносная сила инерции, возникающая за счет воздействия измеряемого датчиком ускорения. Сила инерции P_a может быть представлена в различных формах:

Pa = m⋅a = a⋅ρ ⋅V = a⋅ ρ⋅ H ⋅ S , где m – масса чувствительного элемента (ЧЭ), a – измеряемое ускорение, ρ – плотность материала ЧЭ, V – объем ЧЭ, H – толщина ЧЭ, S – площадь поверхности ЧЭ.

Таким образом, величину перемещения чувствительного элемента под действием только лишь переносной силы инерции на основании формулы (1) можно представить как

y

a

a ⋅ρ⋅ H ⋅ S ⋅ l ³

24 E ⋅ J

или y a

a ⋅ρ⋅ H ⋅ S ⋅ l ³ 2 E ⋅ b ⋅ h ³

Кроме переносной силы инерции на чувствительный элемент датчика действует сила электростатического взаимодействия, возникающая между подвижными обкладками конденсатора [6]. Оценку величины этой кулоновской силы можно провести следующим образом. На обкладки конденсатора подается разность потенциалов U . Чувствительный элемент (подвижная обкладка конденсатора) во время работы датчика всегда остается параллелен основанию прибора (неподвижной обкладке). Данная система обкладок представляет собой плоский конденсатор переменной емкости. Емкость плоского конденсатора может быть найдена как

ε⋅ε ₀ ⋅ S d

где c – емкость конденсатора, ε – диэлектрическая проницаемость окружающей среды, ε ₀ – электрическая постоянная, S – площадь пластин, d – расстояние между пластинами конденсатора.

Кулоновская сила, возникающая между обкладками конденсатора, выражается как

Fe =

ε⋅ε ₀ ⋅ S ⋅ U ²

2 d ²

где F_e – сила притяжения между обкладками, U – разность потенциалов между пластинами.

Сила электростатического взаимодействия является в данном случае «паразитной», так как под ее воздействием чувствительный элемент акселерометра совершает дополнительное перемещение, что вносит ошибку в снимаемый с датчика сигнал и в последующее определение величины действующего ускорения. Для определения величины изменения измеряемых параметров под действием дополнительных кулоновских сил требуется совместное решение упругой задачи об определении поля перемещений чувствительного элемента под действием результирующей силы, складывающейся из воздействия ускорения и дополнительной силы между обкладками конденсатора, а также электростатической задачи об определении силы, возникающей между обкладками конденсатора при появлении на последних разности потенциалов.

Будем считать, что положение чувствительного элемента в пространстве описывается только лишь одной координатой y . Начало отсчета связано с первоначальным недеформированным положением чувствительного элемента датчика, подвешенного на упругих перемычках. Обозначим расстояние между обкладками конденсатора в начальный момент времени, когда на чувствительный элемент не действуют никакие силы и упругие перемычки не деформированы, как А. В этом случае расстояние между обкладками конденсатора d , входящее в формулу (3), можно связать с координатой y , определяющей положение чувствительного элемента в пространстве следующим образом:

d = А + у.

На основании (1) выражение, определяющее перемещение чувствительного элемента датчика под действием сил электростатического взаимодействия, примет вид

l3    2е-е0-А ■ U2

• Уе =---0----- Т~ .

e    24 E ■ J 2 ( А + y e ) ²

Заметим, что в приведенной выше формуле учтено наличие двух систем подвижных обкладок и, следовательно, в два раза увеличено действие электростатических сил и вызываемое ими перемещение чувствительного элемента датчика. В итоге получаем, что для определения результирующего поля перемещений чувствительного элемента микромеханического акселерометра, зависящего от величины действующего ускорения и возникающих между заряженными обкладками конденсатора переменной емкости сил электростатического взаимодействия, требуется решить следующее уравнение:

a-р-H■ А■ l3 _ l3    £■£„ ■ А■ U2

24 E ■ J     24 E ■ J (_{А + у} ) ²

Уравнение (4) можно также выразить через геометрические параметры упругих элементов подвеса:

l ³

2 E ■ b ■ h ³

а'р'H■А+ I

2 ^е ' ^е с ■ ^А ■ ^U

(А + У)2 )

Для отыскания корней уравнения (5) целесообразно применить любой подходящий численный метод решения уравнений подобного типа.

Численное решение уравнения (5) проводилось для следующих значений входящих в него величин: ускорение а изменялось в интервале от - 10 g до + 10 g , где g = 9,8 м/с² - ускорение свободного падения, плотность материала р = 2400 кг/м³, модуль Юнга Е = 1,58■Ю¹¹ Па, толщина чувствительного элемента Н = 0,338■Ю ^{- 3}м, площадь чувствительного элемента А = 1,702 ■Ю ^{- 4} м², длина упругих перемычек l = 0,6 ■ 10 ^{- 3} м, ширина упругих перемычек b = 1,3 ■ 10 ^{- 3} м, высота перемычек h = 8 ■ 10 ^{- 6} м, зазор между обкладками А = 30 ■ 10 ^{- 6} м, разность потенциалов на обкладках U последовательно принималось равной 2, 4, 10 и 20 вольтам, диэлектрическая проницаемость среды £ = 1, электрическая постоянная £ ₀ = 8,854 Ф/м. Результаты решения уравнения (5) представлены в табл. 1. Величины ускорения представлены в долях от ускорения свободного падения g . Перемещения чувствительного элемента в табл. 1, ради наглядности, представлены в микронах. Заметим, из решения уравнения

• (5)    следует, что при отсутствии электростатических сил в случае нулевой разности потенциалов на обкладках конденсатора величина статических перемещений чувствительного элемента, вызванных действием исключительно лишь переносных сил инерции при действующем ускорении + 20 g, составит 27,4 микрон. Запись «прилип»

соответствует ситуации, при которой дополнительные силы электростатического взаимодействия настолько сильно проявляют себя, что под их действием чувствительный элемент датчика совершает дополнительные перемещения, приводящие к необратимому сближению подвижных пластин конденсатора и последующему прилипанию чувствительного элемента к подложке датчика.

Таблица 1

Зависимость перемещений чувствительного элемента ММА от приложенного ускорения и от подаваемого на обкладки напряжения

Ускорение, g , м/с2	Перемещение чувствительного элемента, мкм
	U = 0B	U = 2B	U = 4B	U = 10B	U = 20B
–20	–27,4	–27,3998	–27,3992	–27,3952	–27,3809
–16	–21,92	–21,9198	–21,9192	–21,9141	–21,8968
–12	–16,44	–16,4397	–16,4388	–16,4327	–16,4108
–8	–10,96	–10,9596	–10,9584	–10,9506	–10,9224
–4	–5,48	–5,4795	–5,478	–5,4675	–5,4294
–2	–2,74	–2,7394	–2,7376	–2,7253	–2,6811
0	0	0,0007	0,0028	0,0175	0,0699
2	2,74	2,7409	2,7435	2,7616	2,8263
4	5,48	5,4811	5,4844	5,5073	5,5892
8	10,96	10,9619	10,9674	11,0058	11,1429
12	16,44	16,4435	16,4538	16,5263	16,7851
16	21,92	21,9292	21,9567	22,1777	23,3356
18	24,66	24,6822	24,7512	25,4052	прилип
19	26,03	26,0706	26,2044	прилип	прилип
20	27,4	27,5012	28,0854	прилип	прилип

Как видно из табл. 1, при наличии на обкладках конденсатора разности потенциалов даже при отсутствии ускорения наблюдаются перемещения чувствительного элемента датчика, вызванные взаимным притяжением обкладок за счет электростатических сил, приводящие к снятию с датчика паразитного «шумового» сигнала и возникновению погрешности измерений.

На рис. 4 показаны зависимости перемещений чувствительного элемента акселерометра при различных уровнях напряжений на обкладках. Зависимости на ниже расположенных рисунках приводятся для ускорений, лежащих в интервале [+10g, +20g]. При меньших, а также противоположных по знаку ускорениях расстояние между чувствительным элементом и основанием прибора достаточно велико и эффекты, связанные с электростатическими взаимодействиями, проявляются слабо.

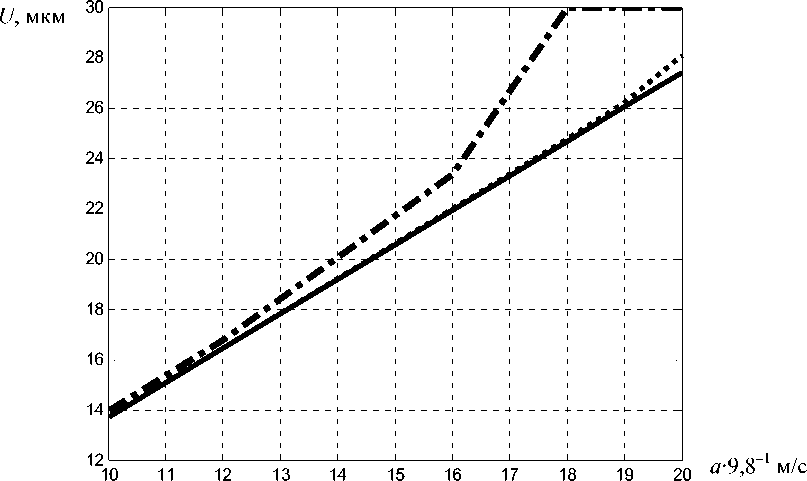
Рис. 4. Зависимость перемещений чувствительного элемента от приложенного ускорения при различных уровнях напряжений:

– U = 0 В; – U = 4 В; – U = 20 В

На рис. 5. представлены зависимости относительной погрешности, вносимой действием кулоновских сил, от приложенного ускорения. Под относительной погрешностью в данном случае понимается разность между перемещениями чувствительного элемента, найденными с учетом влияния электростатических сил и перемещений без учета влияния сил Кулона, отнесенная к тем перемещениям, которые получались бы, если бы силы электростатического взаимодействия себя не проявляли. При разности потенциалов на обкладках конденсатора в 4 В максимальная погрешность, вносимая электростатическими силами, составляет 2,5 %. При разности потенциалов в 20 В относительная погрешность превосходит величину в 20 %.

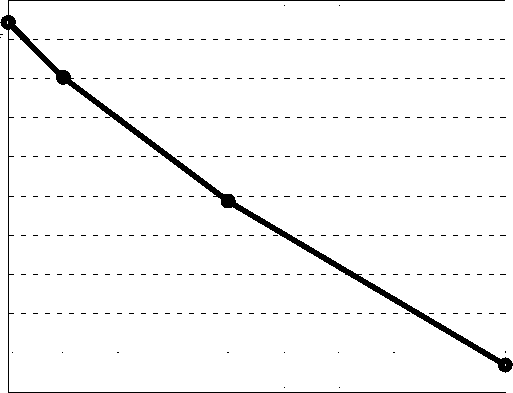
Из решения уравнения (5) может быть определена зависимость ускорения, при котором происходит «прилипание» чувствительного элемента ММА, от величины приложенного напряжения. Результаты расчетов приведены в табл. 2. График зависимости показан на рис. 6.

Таблица 2

Зависимость ускорения, при котором происходит «прилипание» чувствительного элемента ММА, от величины приложенного напряжения

Напряжение, В	2	4	10	20
Ускорение, g, м/с2	20,72	20,02	18,44	16,34

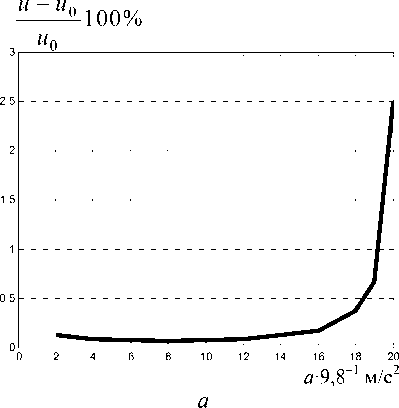
Рис. 5. Зависимость относительной погрешности от величины ускорения: а – при напряжении 4 вольта; б – при напряжении 20 В

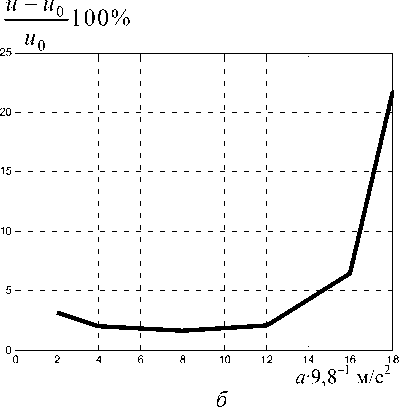
а∙g^-1, м/с^{2    21}

20.5

19.5

18.5

17.5

16.5

2      4      6      8     10     12     14     16     18     20

U , В

Рис. 6. Зависимость ускорения, при котором происходит «прилипание» чувствительного элемента ММА, от величины приложенного напряжения

В результате решения уравнения (5), основанного на аналитическом описании характера деформирования и полей перемещений чувствительного элемента микроакселерометра, получены следующие результаты. Определены зависимости перемещений чувствительного элемента (ЧЭ) ММА от приложенного ускорения и от подаваемого на обкладки прибора напряжения. Показана практически линейная зависимость между перемещением чувствительного элемента датчика и приложенным ускорением при условии достаточной удаленности друг от друга противоположно заряженных обкладок конденсатора. Продемонстрирована нелинейность перемещений ЧЭ при больших положительных ускорениях и большой разности потенциалов на обкладках. Определены относительные погрешности измерений, вносимые действием дополнительных к инерционным электростатических сил. Построены графики данных зависимостей. Найдены соответствующие определенным значениям разности потенциалов величины ускорений, при которых происходит сближение заряженных обкладок конденсатора и их последующее «слипание». Показан механизм образования «шумового» сигнала датчика при отсутствии действующего ускорения, определена его величина.