Аналитическое решение задач устойчивости упругих систем при односторонних ограничениях на перемещения

Решение классических задач на устойчивость упругих систем приводит к проблеме на собственные значения линейных операторов. Задачи устойчивости и закритического поведения упругих систем при наличии односторонних ограничений на перемещения сводятся к нахождению и исследованию точек бифуркации нелинеаризируемых уравнений или к определению параметров, при которых вариационные задачи с ограничениями на искомые функции в виде неравенств имеют не единственное решение. В отличие от классических задач на устойчивость, при наличии односторонних связей необходимо находить точки бифуркации решения задач оптимизации, в которых имеются ограничения в виде неравенств.

В работе получены новые результаты в области устойчивости упругих систем с односторонним подкреплением. Аналитически решена проблема устойчивости сжимаемых продольной силой стержней, находящихся в упругой среде, прогибы которых с одной стороны ограничены жестким препятствием. Исследовано влияние граничных условий на величину критической силы. Также рассмотрена задача устойчивости кольца, нагруженного нормаль- ным давлением и подкрепленного упругими нитями.

• 1.    Устойчивость сжимаемых продольной силой стержней при односторонних ограничениях на перемещения

Пусть стержень длины ℓ , находящийся в упругой среде с жесткостью C , нагружен продольной силой P . Обозначим через D – жесткость стержня при изгибе. Введем в рассмотрение функционал

J(w) = - / (Dw"2 + Cw2 — Pw2)dx.(1)

Предположим, что прогиб стержня w с одной стороны ограничен жестким препятствием так, что w(x) > 0, x G [0, I].(2)

Расчет на устойчивость стержня сводится к нахождению минимальной силы P , при которой вариационная задача

J(w) ^ min

w при ограничении (2) имеет нетривиальное решение. В работе рассмотрено три вида граничных условий:

• • граничные условия жесткой заделки:

w (0) = w ( I ) = 0 , w ' (0) = w ' ( I ) = 0 .     (4)

• •    Граничные условия шарнирного опирания:

w (0) = w ( I ) = 0 , w '' (0) = w '' ( I ) = 0 .    (5)

• •    Граничные условия жесткой заделки при x = 0 с граничными условиями свободного края при x = ℓ :

При этом условии общее решение уравнения (9) имеет вид

w ( x ) = c i sin( m i x ) + c 2 sin( m 2 x ) +

+ c 3 cos( m 1 x ) + c 4 cos( m 2 x ) ,        (11)

где

w (0) = 0 ,

I w ' (0) = 0 ,

) w '' ( I ) = 0 ,

[ w ''' ( I ) + Pw ( I ) = 0 .

^{m 1} = 'j T ⁺ VS

-

ω,

^{m 2} = 'j T ^- \ " 4

-

ω.

1.1. Устойчивость стержня при односторонних ограничениях на перемещения с граничными условиями жесткой заделки

Очевидно, что определение критической силы сводится к задаче изопериметрического типа:

J(w) = - / (Dw"2 + Cw2)dx ^ min (7) 2 Jo при ограничении

J i ( w ) = - / w ' ² dx = 1            (8)

2 Jo и выполнении условий (2) и (4).

Решение экстремальной проблемы (7) , (8) при ограничениях (2) , (4) существует [1], ибо множество функций w G W ^[0 , I ] , удовлетворяющих (2) и (8) , является слабым компактом, a функционал J ( w ) , в этом случае, - выпуклым. Известно, что непрерывный выпуклый функционал достигает своего минимума на любом слабо компактном множестве. Здесь W ₂[0 ,1 ] - пространство функций Л.С. Соболева, имеющих на [0 , I ] обобщенные суммируемые с квадратом первую и вторую производные (первая производная абсолютно непрерывна) и удовлетворяющих условию (2) .

Решение задачи (7), (8), (2), (4) можно искать среди функций строго положительных на интервале (0, 11), 0 < 11 < I и тождественно равных нулю вне этого интервала [1]. Так как w > 0 при x G (0, 11), то прогиб удовлетворяет уравнению Эйлера на этом интервале wIV + ww + р2 w'' = 0,           (9)

где w = C/D, р ² = X/D, X - множитель Лагранжа для ограничения изопериметрического типа (8) . В этом случае (9) является уравнением равновесия сжимаемого продольной силой стержня, находящегося в упругой среде. Заметим также, что (9) совпадает с уравнением равновесия цилиндрической оболочки сжимаемой продольной силой в осесимметричном случае.

Можно показать, что для существования нетривиального решения уравнения (9) при граничных условиях (4) или (5) необходимо выполнение неравенства р2 > 2VW.                (10)

Учитывая, что w ( x ) >  0 для любого x G (0 , 1 1 ) и w ( x ) = 0 при x G ( 1 1 , I ) , то 1 1 либо совпадает с I , либо находится из решения задачи

J ( w ) = - / ( w '' ² + ww ² ) dx ^ min ² Jo                          ^w,¹ 1

при ограничении

J ( w ) = - I w ' ² dx = 1 .

2 o

Из условия минимума по 1 1 в задаче (13) - (14) и с учетом того, что w ( 1 1 ) = 0 , w ' ( 1 1 ) = 0 , из (13) получаем еще одно граничное условие: w '' ( 1 1 ) = 0 . Таким образом, функция w ( x ) является дважды непрерывно дифференцируемой на всем интервале [0 , I ] и удовлетворяет следующим условиям:

Г w (0) = w ( 1 1 ) = 0 ,

< w ' (0) = w ' ( 1 1 ) = 0 ,             (15)

I w '' ( 1 1 ) = 0 .

Подставляя (11) в граничные условия (15) , получаем систему уравнений относительно произвольных постоянных c ₁ , c ₂ , c ₃ , c ₄ и ℓ ₁

' c 3 + c 4 = 0, m1c1 + m2c2 = 0, c 1 sin y + c2 sin z + c3 cos y + c4 cos z = 0, c 1 m 1 cos y + c2 m 2 cos z — c3 m 1 sin y— —c4 m 2 sin z = 0, c 1 m 1 sin y + c2 m2 sin z + c3 m 1 cos y+

+ c ₄ m ² ₂ cos z = 0 ,

(16) где y = m ₁ 1 ₁ , z = m ₂ 1 ₁ . Рассматривая первые четыре уравнения относительно неизвестных c ₁ – c ₄ и приравнивая определитель матрицы коэффициентов к нулю, получаем, что для существования нетривиального решения необходимо, чтобы

2 zy (1 — cos z cos y ) — ( z ² + y ² ) sin z sin y = 0 . (17)

Если же рассмотреть первое, второе, третье и пятое уравнения системы (16), то приходим к уравнению z cos z sin y — y sin z cos y = 0.       (18)

Минимальной критической силе соответствует решение системы уравнений (17) , (18)

y = 3 п, z = п, т.е. 3 п = m 1 1 1 , п = m 2 1 1 .

Используя равенства (12) , находим

ρ

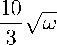
^п

^{1 1}    ^.

Если ℓ 1 < ℓ, то выражение для прогиба принимает вид

w ( x ) = c • sin ³ ( m 2 x ) H ( 1 1 — x ) , x G [0 ,l ] , (20) где m 2 = 4 /w/ V3 , H ( t ) — функция Хевисайда.

1.2. Устойчивость стержня при жестких ограничениях на перемещения с граничными условиями шарнирного опирания

В этом случае

дает значение критической силы. Подбирая i, j таким образом, чтобы р ² = Х/D было минимальным, а функция w ( x ) (26) была неотрицательной, находим

2   5             _х 2 П

^Р = 2 ^ ^{1 1} = W .

Если ℓ 1 < ℓ, то прогиб задается формулой

w ( x ) = c ^2sin ⁿx + sin - yx^ H ( l 1 — x ) , ℓ 1           ℓ 1

Г w (0) = w ( l 1 ) = 0 ,

J w '' (0) = w '' ( l 1 ) = 0 ,             (21)

I w ' ( 1 1 ) = 0 .

c> 0 .

1.3. Устойчивость стержня при жестких

Тогда в системе уравнений (16) необходимо заменить второе уравнение на m 1 c 3 + m 2 c 4 = 0 , откуда, с учетом первого уравнения, получаем, что c 3 = c 4 = 0 и система (16) заменяется на следующую:

{ c 1 sin y + c 2 sin z = 0 , c i m i cos y + c 2 m 2 cos z = 0 ,       (22)

c 1 m 1 sin y + c 2 m 2 sin z = 0 .

ограничениях на перемещения с граничными условиями свободного края

В случае граничных условий жесткой заделки при x = 0 и граничных условий свободного края при x = l выполнены равенства

w (0) = 0 ,

I w ' (0) = 0 ,

) w '' ( l ) = 0 ,

[ w ''' ( l ) + Pw' ( l ) = 0 .

Для существования нетривиального решения последней системы необходимо, чтобы

det ^

sin y m1 cos y

sin z m2 cos z

=0

При данных граничных условиях неравенство (10) заменяется на р2 < 2Vw, и общее решение уравнения (9) имеет вид:

w ( x ) = c 1 e ^ax sin( ex ) + c ₂ e ^ax cos( Px )+

sin y det m2 sin y

sin z m ² ₂ sin z

)=0 .

Откуда получаем два уравнения

m 2 cos z sin y = m 1 cos y sin z, m ² ₂ sin y sin z = m ² ₁ sin y sin z.

Из второго уравнения последней системы

следует,

что sin y = 0 или sin z = 0 . Если sin y = 0 , то из первого уравнения имеем sin z = 0 (ибо в противном случае cos y = 0 , что невозможно), поэтому

y = m 1 l 1 = ni, z = m 2 l 1 = nj, i,j = 1 , 2 ,...

.

Из (25) и второго уравнения системы (22) находим m1

c 2 = —c 1 в , m2

где

в = Г 1,если (i — j) -четное число, в = 1 — 1, если (i — j) - нечет. число, а из (11) получаем w (x) = c 1 ( sin m 1 x — в —1 sin m2 x ) , m2

0 < m 2 x < nj, j = 1 , 2 ,.. ..

Обозначим а = m 1 m - ¹ = ij ла (12) с учетом того, что

9   1 + а2 .— р = ----шш

α

-

¹ , тогда форму-

+ c 3 e ^{- a:x} sin( Px ) + c 4 e ^{- ax} cos( Px ) ,    (29)

где а =2 ^ 2 Vw — P2, P =2 У 2 V^ + р2.   (30)

Будем считать, что существует участок полного прилегания к стенке, т.е.

w ( x ) = 0 , x G [0 ,l 1 ] , и w ( x ) >  0 , x G ( 1 1 ,l ] .

Как и выше, w = 0, w' = 0, w'' = 0 при x = 11.

Таким образом, имеем две системы уравнений:

f w ( 1 1 ) = 0 , I w ' ( 1 1 ) = 0 , 1 w '' ( l ) = 0 , [ w ''' ( l )+ Pw ' ( l ) = 0 ,

и

w ( l 1 ) = 0 ,

I w '' ( 1 1 ) = 0 ,

^ w '' ( l )    0 ,

[ w ''' ( l ) + Pw ' ( l ) = 0 .

Для существования нетривиального решения системы необходимо, чтобы определители матрицы коэффициентов при c 1 – c 4 были равны нулю. Ясно, что в уравнениях (32)-(33) можно положить l 1 = 0 (для этого достаточно заменить x на x — 1 1 ), тогда l будет неизвестной величиной, подлежащей определению. Положим l = l — 1 1 . Определитель системы (32) имеет вид:

△ 1 ( ш, H, р ) = cos ² ( pl)(шр ² — Vwр 4 + 2 Vw ³ ) +

1       7                 1.1                   1         ₇

⁺2 e ^al ( V^ - 2 шр ² - 2 Vwp ^{4 )} + 2 e ^al ( V^ ³ -

- 2 шр2 - 2 V^p4) + V^ - 2 шр2 + 2 Vwp4, а определитель системы (33) равен

△ 2 ( ш,l,p ) = 2 sin( в.в(p ² ш - p ⁴ VW + 2 Vw ³ ) +

+ | e ^al a ( p ² ш + p ⁴ VW - 2 VШ ³ ) -

1         7

- 4 e   ^l a(p ² ш + p Vш - 2у/ ш ³ ) .

Определители △ ₁ ( ш,l,p ) и △ ₂ ( ш,l,p ) были вычислены с помощью системы MAPLE. Таким образом, для нахождения I и p ² имеем систему двух нелинейных уравнений:

△ 1 ( ш,l,p ) = 0 , △ 2 ( ш,l,p ) = 0 .     (34)

Система уравнений (34) решалась методом Ньютона. Результаты вычислений приведены в табл.1.

Таблица 1

Значения критической силы в зависимости от жесткости среды ω

N	1	2	3	4	5	6
ω	100	200	350	450	550	800
1	0.745	0.627	0.545	0.512	0.487	0.443
p 2	12.6	17.8	23.5	26.7	29.5	35.6
p 2	11.9	15.6	19.5	21.8	23.8	28.5

В табл. 1 значения p ² соответствуют критической нагрузке стержня при наличии односторонних ограничений на перемещения при различной жесткости среды ω . Для сравнения, в последней строке приведены значения критической силы P = p ² для стержня, находящегося в упругой среде, при отсутствии односторонних ограничений на перемещения.

На рис. 1 показано различие форм равновесия стержня после потери устойчивости при наличии односторонних ограничений на перемещения и без ограничений.

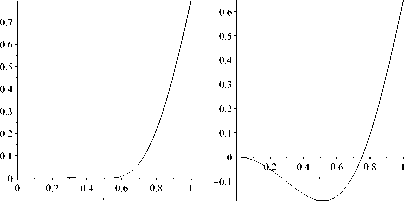
Рис. 1. Форма равновесия стержня после потери устойчивости при наличии односторонних ограничений на перемещения (слева) и без ограничений на перемещения (справа).

2.    Устойчивость колец с односторонним подкреплением

Рассмотрим задачу устойчивости упругих колец, подкрепленных упругими нитями, которые не воспринимают сжимающих усилий.

Пусть один конец нити прикреплен к неподвижному центру кольца, другой — к некоторой точке кольца. Предположим, что нить является нерастяжимой, т.е. в результате деформации расстояние между центром кольца и точкой прикрепления не может увеличиваться. Обозначим через ϑ центральный угол, а через w ( 9 ) радиальное перемещение точек кольца. Наконец, предположим, что нити расположены так часто, что их можно считать непрерывно распределенными по кольцу. Тогда задача на устойчивость сводится к отысканию таких значений силы P, при которых вариационная проблема

J ⁽ w ) Х¹ / ⁽ w ’’ ⁺ w ^{) 2} d^9-

-

P С ² \ 2 2 У, ⁽ w

- w ² ) d9 ^ min w

имеет нетривиальное решение при граничных условиях периодичности и ограничениях

w ( 9 ) <  0 .                   (36)

Здесь B – жесткость на изгиб в плоскости кольца, а R - радиус кольца. Первый интеграл в (35) представляет собой упругую энергию, второй – работу сил нормального давления.

Выпишем уравнение Эйлера для функционала (35) :

w ^IV + (2 + k ² ) w ^H + (1 + к ² ) w = 0 , (37) где к ² = PR ³ . Соответствующее характеристическое уравнение

X ⁴ + (2 + к ² ) X ² + (1 + к ² ) = 0

имеет решение

X i , 2 = ±i ; X 3 , 4 = ± V1 + к ² i.

Тогда функция прогиба представима в виде w = Ai sin 9+A2 cos 9+A3 sin a9+A4 cos a9, (38)

где a = V 1 + к ² .

Зафиксируем некоторый угол в >  0 . Будем считать, что как и в случае стержней w ( 9 ) <  0 , 9 Е (0 , в ) и w ( 9 ) = 0 , 9 Е ( в, 2 п ) . Первая производная w ‘ ( 9 ) должна быть непрерывной при 9 Е (0 , 2 п ) , тогда функция w удовлетворяет граничным условиям

w (0) = 0 , w ‘ (0) = 0 , w ( в ) = 0 , w ‘ ( в ) = 0 . (39)

Подставляя (38) в (39) , получим систему линейных уравнений

A 2 + A 4 = 0 ,

A 1 + aA 3 = 0 ,

A 1 sin в + A ₂ cos в + A 3 sin( ав ) +

+ A ₄ cos( ав ) = 0 ,

A 1 cos в - A ₂ sin в + aA 3 cos( ав ) -- aA 4 sin( ав ) = 0 .

После упрощения, имеем

A a (sin( ав ) — а sin в ) +

+ A 4 (cos( ав ) — cos в ) = 0 , A з ( а cos( ав ) — а cos в ) + + A 4 (sin в — a sin( ав )) = 0 .

Система уравнений имеет нетривиальное решение, если ее определитель равен нулю, т.е.

d ( а ) = — 2 а cos( ав ) cos в + 2 а—

— sin( ав ) sin в — а ² sin( ав ) sin в = 0 .     (42)

Решая уравнение (42) относительно неизвестной а , получим функцию а = а ( в ) . При заданном β уравнение имеет бесконечное число корней. Очевидно, что а = 1 является корнем уравнения при любом в . Заметим, что а = 1 соответствует сила P , равная нулю. Далее, находим форму прогиба по формулам (38) . Несложно убедиться, что формула (38) при а = 1 дает перемещение кольца какжестко-го целого. Следовательно, надо находить минимальный корень уравнения (42) , удовлетворяющий условию а >  1 . Также необходимо выполнение знаковых ограничений (36) . Чем больше угол в , тем меньше k ² , а значит и сила P . Значения критического параметра α в зависимости от значений угла β приведены в табл. 2.

Таблица 2

Значения α в зависимости от угла β

β	π 4	π 2	3 π 4	π	5 π 4
α	4.9801	4.2915	3.2136	3	2.4841

Численные эксперименты при β > π показали, что график w будет менять знак на интервале (0 , в ) , т.е. ограничения неотрицательности на функцию w не будут выполняться.

Рис. 2. График определителя d ( а ) при в = 1 • 25 п (слева); форма прогиба w при в = п (справа).

График функции d ( а ) при в = 5П приведен на рис. 2 слева. Уравнение d ( а ) = 0 имеет, в данном случае, два корня, значения которых меньше 3: а 1 = 2 . 4841 и а 2 = 2 . 8413 .

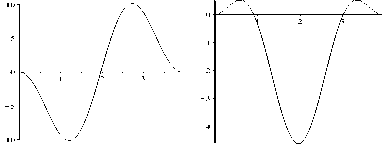
Рис. 3. Форма прогиба w: при в = 1 • 25 п , а = 2 . 4841 (слева), при в = 1 • 25 п , а = 2 . 8413 (справа).

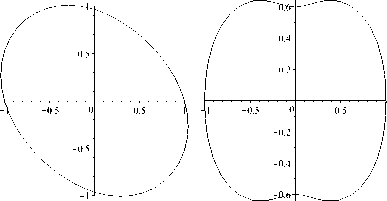
Рис. 4. Форма равновесия кольца в отсутствии подкрепления (слева); форма равновесия кольца, подкрепленного упругими нитями (справа).

Графики собственной функции w ( $ ) уравнения (37) приведены на рис. 3: слева - при а 1 = 2 . 4841 , справа - при а 2 = 2 . 8413 . В обоих случаях w ( $ ) меняет знак на интервале [0 , в ] , т.е. ограничение (36) не выполняется. Знаковые ограничения на собственную функцию будут выполнены, если в 6 (0 , п ] . Ясно, что минимальной критической силе соответствует значение параметра а = 3 при в = п . В этом случае критическое давление для неподкреп-ленного кольца равно

Р= 3в

P R ³ .

График функции прогиба при в = п и а = 3 приведены на рис. 2 справа. Различие форм равновесия кольца проиллюстрировано на рис. 4: слева – кольцо без поддерживающих нитей, справа – с нерастяжимыми нитями.