Аналитическое выражение матрицы узловых проводимостей трансформатора со схемой соединения обмоток «звезда - звезда»
Автор: Солдатов В.А., Чебесов Е.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Технические науки: Процессы и машины агроинженерных систем
Статья в выпуске: 6, 2015 года.
Бесплатный доступ
Получено аналитическое выражение для матрицы узловых проводимостей трансформатора со схемой соединения обмоток «звезда-звезда», не требующее процедуры обращения матриц.
Трансформатор, аварийный режим, несимметричный режим, метод фазных координат, матрица узловых проводимостей, схема соединения обмоток, аналитическое выражение
Короткий адрес: https://sciup.org/14084357
IDR: 14084357 | УДК: 621.315
Текст научной статьи Аналитическое выражение матрицы узловых проводимостей трансформатора со схемой соединения обмоток «звезда - звезда»
В основном методики расчета несимметричных аварийных режимов основываются на матрицах узловых проводимостей элементов электрической сети (линий, двухобмоточных трансформаторов, трехобмоточных трансформаторов, автотрансформаторов, компенсирующих устройств, нагрузок, источников реактивной мощности и др.). По матрицам узловых проводимостей строят схемы замещения как самих элементов сети, так и сети в целом. Таким образом, для каждого элемента сети необходимо знать матрицу узловых проводимостей.
Наиболее сложными для моделирования являются трансформаторы. В большинстве методик, чтобы найти матрицу узловых проводимостей трансформатора, используют процедуру обращения комплексной матрицы собственных и взаимных сопротивлений трансформатора. Это вызывает определенные трудности, так как требуется компьютерная программа обращения матриц. В данной статье поставлена задача получения аналитических выражений для матрицы узловых проводимостей трансформатора в фазных координатах без необходимости использования процедуры обращения матрицы.
В сетях 0,38 кВ используется потребительский трансформатор со схемой соединения обмоток «звезда–звезда». Получим матрицу узловых проводимостей для данного трансформатора. При необходимости нулевую точку трансформатора на выходе можно заземлить. В этом случае получим трансформатор со схемой соединения «звезда–звезда с нулем» [4].
Расчетная схема данного трансформатора представлена на рисунке. На этой схеме номера узлов указаны в кружках, а номера ветвей в квадратах. На схеме обозначены собственные сопро- тивления входной (Zc1) и выходной (Zc2) обмоток и взаимные (Zm) сопротивления между ними. Эти сопротивления можно определить по паспортным данным трансформатора.
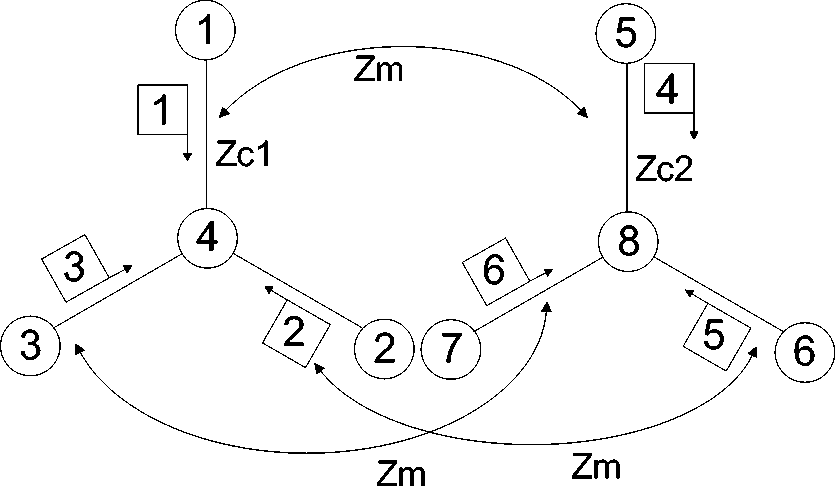
Расчетная схема трансформатора «звезда–звезда»
После нумерации узлов и ветвей трансформатора можно составить матрицу соединений (инциденции) М
|
Г 1 |
0 |
0 |
0 |
0 |
0 ■ |
||
|
0 |
1 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
1 |
0 |
0 |
0 |
||
|
- 1 |
- 1 |
- 1 |
0 |
0 |
0 |
||
|
M = |
0 |
0 |
0 |
1 |
0 |
0 |
(1) |
|
0 |
0 |
0 |
0 |
1 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
1 |
||
|
L 0 |
0 |
0 |
- 1 |
- 1 |
- 1 \ |
Если известна матрица соединений М и матрица собственных и взаимных сопротивлений ветвей ZV , то матрица узловых проводимостей трансформатора определится как
Y = M • ZV 1 • MT .
Данный трансформатор может быть трехбакового исполнения (обмотки каждой из фаз А, В, С размещены в трех отдельных баках) и однобакового исполнения (все обмотки размещены в одном баке). Рассмотрим оба указанных случая исполнения трансформатора.
Трехбаковое исполнение трансформатора . Для двухобмоточного трехфазного трехбакового трансформатора матрица сопротивлений ветвей ZV имеет вид
|
■ Zc1 |
0 |
0 |
Zm |
0 |
0 ‘ |
||
|
0 |
Zc 1 |
0 |
0 |
Zm |
0 |
||
|
0 |
0 |
Zc 1 |
0 |
0 |
Zm |
(3) |
|
|
ZV = |
Zm |
0 |
0 |
Zc 2 |
0 |
0 |
|
|
0 |
Zm |
0 |
0 |
Zc 2 |
0 |
||
|
L о |
0 |
Zm |
0 |
0 |
Zc 2 |
Обратная матрица ZV-1 будет иметь вид
|
■- Zc 2 |
0 |
0 |
Zm |
0 |
0 ’ |
|||
|
0 |
- Zc 2 |
0 |
0 |
Zm |
0 |
|||
|
. 1 |
0 |
0 |
Zc 2 |
0 |
0 |
Zm |
(4) |
|
|
ZV-1 = - |
||||||||
|
d |
Zm |
0 |
0 |
- Zc1 |
0 |
0 |
||
|
0 |
Zm |
0 |
0 |
- Zc 1 |
0 |
|||
|
l 0 |
0 |
Zm |
0 |
0 |
- Zc 1 |
|||
|
Здесь |
d = Zm |
2 - Zc1 |
Zc 2 . |
(5) |
Подставляя (1), (4) и (5) в (2), получим искомую матрицу узловых проводимостей Y транс- форматора
|
"- Zc 2 |
0 |
0 |
Zc 2 |
Zm |
0 |
0 |
- Zm |
||
|
0 |
- Zc 2 |
0 |
Zc 2 |
0 |
Zm |
0 |
7 - Zm |
||
|
0 |
0 |
- Zc 2 |
Zc 2 |
0 |
0 |
Zm |
- Zm |
||
|
1 |
Zc 2 |
Zc 2 |
Zc 2 |
- 3 • Zc 2 |
- Zm |
- Zm |
- Zm |
3 • Zm |
|
|
Y = - |
(6) |
||||||||
|
d |
Zm |
0 |
0 |
- Zm |
- Zc1 |
0 |
0 |
Zc 1 |
|
|
0 |
Zm |
0 |
- Zm |
0 |
- Zc 1 |
0 |
Zc 1 |
||
|
0 |
0 |
Zm |
- Zm |
0 |
0 |
- Zc 1 |
Zc 1 |
||
|
_- Zm |
- Zm |
- Zm |
3 • Zm |
Zc 1 |
Zc 1 |
Zc 1 |
- 3 • Zc1 |
Разделяя (6) на блоки относительно узлов входа (1–4) и узлов выхода (5–8), получим блоки матрицы узловых проводимостей трансформатора
|
’- Zc 2 0 0 Zc 2 ‘ |
Zm 0 0 - Zm |
||
|
1 |
0 - Zc 2 0 Zc 2 |
1 |
0 Zm 0 - Zm |
|
Y 11 = - • |
Y 12 = - • |
||
|
d |
0 0 - Zc 2 Zc 2 |
d |
0 0 Zm - Zm |
|
Zc 2 Zc 2 Zc 2 - 3 • Zc 2 |
- Zm - Zm - Zm 3 • Zm |
|
Zm |
0 |
0 |
— Zm' |
’— Zc1 |
0 |
0 |
Zc1 ' |
|||
|
1 |
0 |
Zm |
0 |
- Zm |
1 |
0 |
— Zc1 |
0 |
Zc 1 |
(7 |
|
Y 21 = - • |
Y 22 = - • |
|||||||||
|
d |
0 |
0 |
Zm |
— Zm |
d |
0 |
0 |
— Zc1 |
Zc 1 |
|
|
— Zm |
- Zm |
- Zm |
3 • Zm _ |
_ Zc 1 |
Zc 1 |
Zc 1 |
— 3 • Zc1 _ |
Таким образом, полученные аналитические выражения (6) – (7) позволяют определять матрицу узловых проводимостей трансформатора «звезда–звезда» в трехбаковом исполнении без необходимости обращения матриц.
Однобаковое исполнение трансформатора . Как показано в [3], для однобакового трансформатора можно принять, что взаимные сопротивления отличаются от соответствующих собственных сопротивлений на одно и то же число N . В этом случае для двухобмоточного трехфазного однобакового трансформатора матрица сопротивлений ветвей ZV0 будет иметь вид
|
■ Zc1 Zc1 • N Zc1 • N Zm Zm • N Zm • N “ Zc1 • N Zc1 Zc1 • N Zm • N Zm Zm • N Zc1 • N Zc1 • N Zc1 Zm • N Zm • N Zm |
|
|
ZV 0 = |
Zm Zm • N Zm • N Zc 2 Zc 2 • N Zc 2 • N () Zm • N Zm Zm • N Zc 2 • N Zc 2 Zc 2 • N Zm • N Zm • N Zm Zc 2 • N Zc 2 • N Zc 2 |
Обратная матрица ZV0-1 будет иметь вид
|
’— Zc 2 • ( N + 1) — N • Zc 2 — N • Zc 2 — Zm • ( N + 1) N • Zm N • Zm ’ — N • Zc 2 — Zc 2 • ( N + 1) — N • Zc 2 N • Zm — Zm • ( N + 1) N • Zm |
|
|
. i ZV0 -1 = — d • dn |
— N • Zc 2 — N • Zc 2 — Zc 2 • ( N + 1) N • Zm N • Zm — Zm • ( N + 1) (9) — Zm • ( N + 1) N • Zm N • Zm Zc1 • ( N + 1) — N • Zc1 — N • Zc1 N • Zm — Zm • ( N + 1) N • Zm — N • Zc1 Zc1 • ( N + 1) — N • Zc1 _ N • Zm N • Zm — Zm • ( N + 1) — N • Zc1 — N • Zc1 Zc1 • ( N + 1) _ |
Здесь d = Zm2 - Zc1 • Zc2 ; dn = (N -1) • (2N +1) (10)
.
Подставляя (1), (9) и (10) в (2), получим искомую матрицу узловых проводимостей трансформатора Y0, которую разделим на блоки
Y0 =
Y011
Y 021
Y 012
Y 022
В (11) блоки матрицы Y0 равны
•
—
•
—
•
•
Y 021 = — d • dn
Y 012 = 1
d • dn
Y 011 = — d • dn
Y 022 = — d • dn
|
Zc 2 • ( N + 1) |
— N • Zc 2 |
— N • Zc 2 |
Zc 2 • ( N — 1) |
|
— N • Zc 2 |
Zc 2 • ( N + 1) |
— N • Zc 2 |
Zc 2 • ( N — 1) |
|
— N • Zc 2 |
— N • Zc 2 |
Zc 2 • ( N + 1) |
Zc 2 • ( N — 1) |
|
Zc 2 • ( N — 1) |
Zc 2 • ( N — 1) |
Zc 2 • ( N — 1) - |
3 • Zc 2 • ( N — 1) |
|
Zm • ( N + 1) |
N • Zm |
N • Zm |
— Zm • ( N — 1) ’ |
|
N • Zm |
— Zm • ( N + 1) |
N • Zm |
— Zm • ( N — 1) |
|
N • Zm |
N • Zm |
— Zm • ( N + 1) |
— Zm • ( N — 1) |
|
Zm • ( N — 1) |
— Zm • ( N — 1) |
— Zm • ( N — 1) |
3 • Zm • ( N — 1) |
|
- Zm • ( N + 1) |
N • Zm |
N • Zm |
— Zm • ( N — 1) |
|
N • Zm |
— Zm • ( N + 1) |
N • Zm |
— Zm • ( N — 1) |
|
N • Zm |
N • Zm |
— Zm • ( N + 1) |
— Zm • ( N — 1) |
|
- Zm • ( N — 1) |
— Zm • ( N — 1) |
— Zm • ( N — 1) |
3 • Zm • ( N — 1) |
|
’ Zc 1 • ( N + 1) |
— N • Zc1 |
— N • Zc1 |
Zc1 • ( N — 1) ’ |
|
— N • Zc 1 |
Zc1 • ( N + 1) |
— N • Zc 1 |
Zc1 • ( N — 1) |
|
— N • Zc 1 |
— N • Zc1 |
Zc1 • ( N + 1) |
Zc1 • ( N — 1) |
|
Zc 1 • ( N — 1) |
Zc1 • ( N — 1) |
Zc1 • ( N — 1) — |
3 • Zc1 • ( N — 1) |
Выводы. Таким образом, полученные аналитические выражения (8) – (12) позволяют определять матрицу узловых проводимостей трансформатора «звезда–звезда» в однобаковом исполнении без необходимости обращения матриц.
Полученные аналитические выражения (3)–(12) облегчают задачу расчета аварийных несимметричных режимов электрических сетей с данным трансформатором, так как не требуется процедура обращения комплексных матриц.


