Аналитика элементарных модулей

Семенов Б.П.; Semyonov B.P.

Научные статьи \ Прикладные науки. Медицина. Технология \ Инженерное дело. Техника в целом \ Общее машиностроение. Ядерная технология. Электротехника. Технология машиностроения

Аналитика элементарных модулей

Автор: Семенов Б.П.

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Рубрика: Механика и машиностроение

Статья в выпуске: 2 т.4, 2002 года.

Бесплатный доступ

Аналитические решения задачи о функциях и производных первого и второго порядков функций векторных модулей могут быть использованы в системах управления, в частности, робототехнических систем.

Короткий адрес: https://sciup.org/148197713

IDR: 148197713 | УДК: 621.01

Analytics of elementary modules

Analytical decisions of a task on functions and derivatives of the first and second orders of functions of vector modules represent practical interest, in particular, at the analysis and synthesis various on structure and purpose of mechanisms.

Текст научной статьи Аналитика элементарных модулей

Самарский государственный аэрокосмический университет

Модуль векторной модели - векторный замкнутый контур или минимальная по составу система взаимо связанных векторных замкнутых контуров с определенностью между функциями и аргументами.

Под определённостью между функцией и аргументом будем понимать возможность вычисления значений функций контура по заданным значениям его аргументов и констант.

Все многообразие векторных модулей можно разделить на одноконтурные (простые) и многоконтурные (с обратными связями).

Элементарный векторный модуль - одноконтурный модуль с числом функций, равным числу измерений контура.

Элементарные плоские и пространственные векторные модули, приведены в табл.1. Практический интерес для определения частных производных представляют приведённые в этой таблице основные аргументы одно- и двухаргументных модулей.

Функции элементарных плоских модулей

Аналитические решения для функций элементарных m-векторных плоских модулей табл.1 получим из условия замкнутости:

∑m pi ⋅cos ϕi = 0, (1) i=1

∑ pi⋅sin ϕi = 0. (2)

i=1

Используем вариант индексации векторов: i = 1, j = 2 и k = 3.

Модуль Пл1 (функции p₁ и ϕ ₁ ). Преобразуем (1) и (2)

p1 ⋅ cos ϕ1 = -X,

p1 ⋅ sin ϕ1 = -Y, где

X= ∑ ^m p_i ⋅ cos ϕ _i,Y= ∑ ^m p_i ⋅ sin ϕ _i, i=2 i=2

тогда p1 = VX2 +Y2 (3)

ϕ ₁ = sign(- ⋅ Ya)rccos(-pX₁/) . (4)

Модуль Пл2 (функции p₁ и p₂ ). Преобразуем (1) и (2)

p1 ⋅ cosϕ(1 - ϕ2 )+ p2 + X = 0 , (5)

p₁ ⋅ sin( ϕ ₁ - ϕ ₂)+Y=0, (6)

где

X=∑ pi ⋅cos( ϕi -ϕ2), i=3

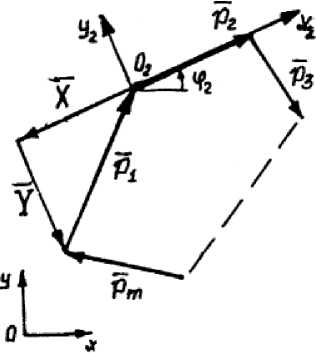
Рис.1. Геометрия модуля Пл2

Таблица 1. Элементарные векторные модули

s m

Св И И

О s

Обобщённый список функций

О П У

S T

u к

Основные аргументы

двухаргументных модулей

одноаргументных модулей

u 1

u 2

u 3

α i

β i

α j

β j

α k

β k

r i1

α i1

β i1

r i2

α i2

β _i2

Пространственные

Пр 1

α i

β i

Пр 2

α i

Пр 3

α i

α j

Пр 4

α i

β j

Пр 5

β i

Пр 6

β i

α j

Пр 7

β i

β j

Пр 8

α i

β i

Пр 9

α i

β i

α j

Пр 10

α i

β i

β j

III

Пр 11

Пр 12

α k

Пр 13

β k

Пр 14

α j

α k

Пр 15

α j

β k

Пр 16

α i

α j

α k

Пр 17

α i

α j

β k

Пр 18

β i

β j

Пр 19

β i

β j

α k

Пр 20

β i

β j

β k

∞

Плоские

u 1

u 2

ϕ i

ϕ j

^pil

ϕ il

^pi2

ϕ i2

Пл 1

ϕ i

Пл 2

Пл 3

Пл 4

Примечание: i 1 и i₂ - индексы векторов, не имеющих параметров-функций.

Y = j pi ■ sin(фi-ф2), p1=-Y/sin>1-^2) (7)

ⁱ⁼³ затем из уравнения (5)

т.е. перейдем к системе координат X2O2Y2

(рис.1), тогда из уравнения (6) получим p 2 ^{= -X-}p 2 ^⋅ cos( ϕ 1 ^- ϕ 2 ) ^{. (8)}

Модуль Пл3 (функции p₁ и ϕ ₂ ). В системе координат X₁O₁Y₁ (рис.2),

X= ∑ ^m p_i ⋅ cos ϕ (_i - ϕ ₁) , i=3

Y= ∑ ^m p_i ⋅ sin ϕ (_i- ϕ ₁) .

i=3

Первый вариант решения (V=1) принимаем при | ϕ ₂ ₁ | > π /2.

Пусть k = 1 при V = 1 и k = -1 при V = 2.

В треугольнике АВО1 ∆p= p22 -Y 2 , тогда p1 =-X+k ⋅ ∆p, (9)

ϕ ₂ = sign(- ⋅ Ya)rccos( ⋅ ∆ kp/p₂) + ϕ ₁. (10)

Модуль Пл4 (функции ϕ ₁ и ϕ ₂ ). Предварительно определим параметры суммарного вектора p_1-2 = p₁ + p₂ .

p 1-2 = VX²+Y² ^,

ϕ _1-2 =sign(- ⋅ Ya)rccos(-pX₁/_-2) , где

X= ∑ ^m p_i ⋅ cos ϕ _i, Y= ∑ ^m p_i ⋅ si ϕ n_i . i=3 i=3

Перейдем к системе координат X1О1Y1 (рис.3).

В треугольнике со сторонами a, b, c , и противолежащими соответственно углами А, В, С:

А = 2 ⋅ arccos л/ p ⋅ (p - a)/bc

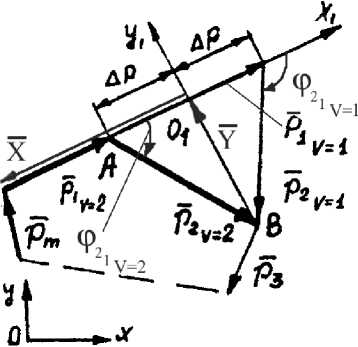
Рис.2. Геометрия модуля Пл3

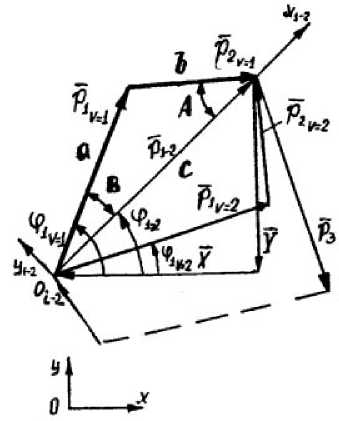
Рис.3. Геометрия модуля Пл4

и B=2 ⋅ arccosp ⋅ (p-b)/a , где p=0,5⋅ (a + b + c)

или при a = p1, b = p2 и с = p1-2 (рис.3)

А =2 ⋅ arccoss ⋅ (p-p₁)/p₂ ,

B=2 ⋅ arccoss⋅ (p-p2)/p1 , где p=0,5⋅ (p1 + p2 + p1-2) , s= p/p1-2 .

Принимаем первый вариант решения

V=1 при ϕ11-2 ≥ 0.

Пусть k = 1 при V = 1 и k = -1 при V = 2, тогда

ϕi= ϕ1-2 + ∆ϕi, (11)

где

i = 1 или 2, ∆ϕ1 =k⋅ B , ∆ϕ2 =-k⋅ A .

Используя отображения пространственного векторного контура на вспомогательной плоскости, представим решение задачи о функциях большинства элементарных пространственных модулей табл.1 в виде следующих параметрических формул.

Модуль Пр1 (функции r₁, α ₂, β ₁ ) .

p4 =∑m ricosαicosβi , j4 = 0, i=2

p5 =∑m ricosαisinβi , j5 = 90°, i=2 5

p2 =∑risinαi , j = 90°.

i = 2 ²

Решение единственное.

(V=1) - при β21-2 ≥

Максимальное число решений ‒ 2.

Модуль Пр2 (функции r ₁ , α ₁ , r ₂ ). m

Модуль Пр7 (функции r₁, β ₁, β ₂ ) .

r ₂ =

∑ricosαisin(βi -β1)

i = 3

cosα2 ⋅ sin(β2 - β1)

∑ri sinαi i=2 ,

sinα1

r 2

(1, 2, …, m) Пp1( r 1 , α 1 , β 1 )

= r1 cosα1

= r2 cosα2

p3 =∑ricosαicosβi , j3 = 0, i=3

Решение единственное.

Модуль Пр3 (функции r₁ , α ₁ , α ₂ ).

∑m ri cosαi sin(βi -β1)

α ₂ = ± arccos ⁱ ⁼ ³

r ₂ ⋅ sin( β ₂ - β ₁)

α 2

(1, 2, …, m) Пp1( r 1 , α 1 , β 1 )

Принимаем: первый вариант решения ( V =1) - при α ₂ ≥ 0 .

Максимальное число решений ‒ 2.

Модуль Пр4 (функции r₁, α ₁, β ₂ ).

p4 = ∑ ricosαisinβi , j4 = 90°.

i = 3

m =4 (1, 2, 3, 4)
m =4 (1, 2, 3, 4)
Пл4( ϕ 1 , ϕ 2 )
V

β 1 = ϕ 1

β 2 = ϕ 2

Принимаем: первый вариант решения ( V =1) - при β ₁ ₂ ≥ 0

Максимальное число решений ‒ 2.

Модуль Пр8 (функции α1, β1, r2). ϕ2 = α2

p3 =∑m ricosαicos(βi-β2), ϕ3 = 0, i=3

-∑ri cosαi sin(βi - β1)

β = arcsin i=3 +

r2 ⋅ cosα2

+ β 1

β2 = β или

β ₂ = 180 ° - β

p4 =∑risinαi, ϕ4 = 0, i=3

p5 = r1 - p4

Принимаем: первый вариант решения

( V =1) - при ϕ 5 ≥ ₂ .

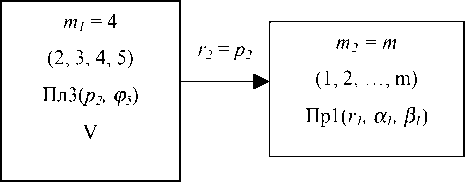
Модуль Пр18 (функции β ₁, β ₂, r₃ ).

r ₃

r1 sinα1 + r2 sinα2 + ∑ri sinαi i=4

sinα3

Максимальное число решений ‒ 2.

Модуль Пр9 (функции α ₁, β ₁, α ₂ ).

m2 = m

(1, 2, …, m) Пp7( r 1 , β 1 , β 2 )

p2 = r2,

p3 =∑m ricosαicos(βi-β2), j3 = 0, i=3

p4 = ∑m ri sinαi , j4 = 0, i=3

p5 = r1 - p4

Принимаем: первый вариант решения ( V =1) ‒ при β ₁₁ _- ₂ ≥ 0.

Максимальное число решений ‒ 2.

Модуль Пр19 (функции β ₁, β ₂, α ₃ ).

- ( r ₁ sin α ₁ + r ₂ sin α ₂ + ∑ r_i sin α _i )

α = arcsin ⁱ ⁼ ⁴

r ₃

α3 = α или

= 180 ° - α

α ₃

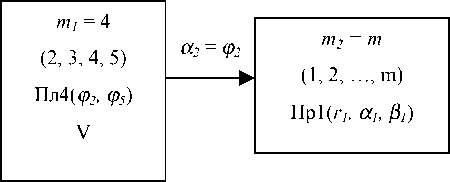
m 2 = m

(1, 2, …, m) Пp7( r 1 , β 1 , β 2 )

Принимаем: первый вариант решения

Принимаем: первый вариант решения ( V =1) - при α ₂ ≥ 0 .

Максимальное число решений ‒ 2.

Модуля Пр10 (функции α ₁, β ₁, β ₂ ).

- r sin α

α1 = arcsin i=2

α 1

m2 = m

(1, 2, …, m) Пp7( r 1 , β 1 , β 2 )

(V=1) ‒ при β11-2 ≥0 и α3 ≥ 2 .

Максимальное число решений ‒ 4.

Прямые аналитические решения для функций модулей Пр12 и Пр13 получены ранее методом Гаусса [1-3], для модулей Пр6, Пр11, Пр14-Пр17, применим метод обращения, при котором одну из функций исходного модуля используем в качестве аргумента обращённого .

Производные первого порядка функций элементарных модулей

Для одноаргументной функции

Принимаем: первый вариант решения ( V =1) - при β ₁₁ _- ₂ ≥ 0.

Максимальное число решений ‒ 2.

dU X) = dU dx dt ∂x dt ,

для многоаргументной функции

dU(x1,

., x_k ) _{= ∑} ^k ∂ U dx j _, j = 1 ∂ ^xj ^dt

т.е. для определения полной производной функции необходимо определить все её частные производные первого порядка.

Дифференцируем уравнения (1) и (2)

dU a1 1 1 dx j +a 21 dU 2 dx j +b 11 = 0, (14) dU a1 1 2 dx j +a 22 dU 2 dx j +b 12 = 0, (15) тогда при i = 1, 2; s = 1, 2 и j = 1, …, k, используя данные табл.2,

QU,A,.

= , dxjA где

Таблица 2. Коэффициенты a. и свободные s члены b1s матриц формулы (16) для плоских модулей

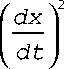
Ui a pk Фк x b1s ai1 cos^k -pk sinфk b11 ai2 sin^k Pk cosфk b12 dU d2 x dx dt ’ d U X) = d U dt dx2

d ² U ( x ₁,..., x_k ) dt ²

A =

A i =

b 1 ₁

a 2 1

“

A ₂ =

^b 1 1

b 1 ₂

j = 1

Для пространственного модуля (i = 1, 2, 3 и s = 1, 2, 3) используем формулу (16) и данные табл.3, при этом

d ² U ( dXj ) ² d U d ² Xj

+ dx 2j dt dx dt2

j V 7 ^j

+ 21 1 d 2 U dx- dx j~1 -2dj+i dx- dx -2 dt dt

1 ₁

2 ₁

3 ₁

“ b i i

^a 2 i

3 ₁

1 ₂

2 ₂

3 ₂

, A 1 =

" ^Ь 1 2

2 ₂

3 ₂

1 ₃

2 ₃

3 ₃

“ ^Ь 1 з

2 ₃

3 ₃

1 ₁

“ ^b 1 i

3 ₁

^a i i

^a 2 i

" ^b 1 i

^A 2 ⁼

1 ₂

“ ^Ь 1 2

3 ₂

, A =

1 ₂

2 ₂

- b_x

1 ₂

1 ₃

“ ^Ь 1 з

3 ₃

1 ₃

2 ₃

— b

1 ₃

Производные второго порядка функций элементарных модулей

Дифференцируем выражения (12) и (13)

т.е. для определения полной производной второго порядка функции необходимо определить все частные производные первого и второго порядков этой функции, как чистые так и смешанные.

Дифференцируем систему уравнений (14) и (15)

d U 1

dx . • dx . j ₁ j ₂

^d U ² + b 2 = 0, (19)

dx . •dx .

d 2U

-----1— + a 2 dx • dx 2 dx • dx j1 j2 j1

= 0, (20)

Таблица 3. Коэффициенты a i и свободные члены b₁ s матриц формулы (16) для пространственных модулей

U i ^a>\	r k	a k	P k	x k b ₁
a i ₁	cos a k sin ^ k	-r k sin a k cos P k	-r k cos a k sin P k	b 1 ₁
a i ₂	sin a k	r k sin a k	0	^b 1 2
a i ₃	cos a k sin ^ k	-r k sin a k sin P k	-r k cos a k cos P k	^b 1 3

∂α _i ∂ b ₁

Таблица 4. Частные производные ^S и ^S матриц формулы (17) для плоских модулей

∂x ∂x j2 j2

x j 1	p k				ϕ k				x j ₁
x j ₂ ∂α i_S ∂ x j ₂	p k	ϕ k	p l	ϕ l	p k	ϕ k	p l	ϕ l	^xj 2 ∂ b 1 _S ∂ x j ₂
∂ a i ₁ ∂ x j ₂	0	-sin ϕ k	0	0	-sin ϕ k	-p k cos ϕ k	0	0	∂ b 1₁ ∂ x j ₂
∂ a i ₂ ∂ x j ₂	0	cos ϕ k	0	0	cos ϕ k	-p k sin ϕ k	0	0	∂ b 1₂ ∂ x j ₂

тогда при i = 1, 2; s = 1, 2; j1 = 1, …, k; j2 = 1, …, k, используя данные табл.4,

где

∂ ² U i ₌ ∆ i

∂ x_j ₁ ∂ x_j ₂ ∆

^b 2 1

= ∑3 ∂αi1 ⋅ ∂Ui + ∂b11 i=1 ∂xj2 ∂xj1 ∂xj2

где

∆=

1 ₁

^α 2 1

- b ₂₁

2₁

1 ₁

- b ₂₁

1 ₂

2 ₂

- b ₂₂

2₂

1 ₂

- b ₂₂

b 2 = ∑ ³ ^∂α ⁱ ² ⋅ ^∂ ^U ⁱ + ^∂ ^b ¹²

2 i=1 ∂xj2 ∂xj1 ∂xj2 ,

при

b =∑2 ∂αi1 ⋅∂Ui + ∂b11

²¹ i = 1 ∂ x_j ₂ ∂ x_j ₁ ∂ x_j ₂

_∑ ³ ∂α i ₃ i = 1 ∂ ^xj 2

∂Ui + ∂b12 ∂xj1 ∂xj2 .

Для каждого одно- и двухаргументно-

b =∑2 ∂αi2 ⋅ ∂Ui + ∂b12

22 i=1 ∂xj2 ∂xj1 ∂xj2 .

го модуля табл.1 на основе приведённых выше общих матричных решений могут быть получены аналитические выражения,

Для пространственного модуля (i = 1, 2, 3 и s = 1, 2, 3) используем данные табл.5 и формулу (17), при этом

минимизированнные по числу вычислительных операций.

Аналитическое и программное обеспечение абстрактных векторных модулей, ис-

∆=

∆ ₂

α 2 ₁

b 2 ₁

α 2 ₁

∆

1 ⁼

пользованное при решении различных научных и инженерных задач теории механизмов, может быть рекомендовано к широкому практическому применению, в частности, применительно к системам управления, например робототехнических систем.

- b21

αα

1 ₁ 2 ₁

∆=

- b21

- b22

- b23