Анализ аберраций третьего порядка линзы Френеля
Автор: Романова Г.Э., Нгуен Н.Ш.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 4 т.47, 2023 года.
Бесплатный доступ
В работе представлены выражения для аберраций третьего порядка поверхности Френеля (коэффициенты Зейделя). Формулы получены в виде, позволяющем выполнять анализ аберраций аналитически, на этапе компоновки и предварительного расчета системы из поверхностей как классических, так и Френеля. В дополнение к пяти основным монохроматическим аберрациям Зейделя классических поверхностей и линейной коме, выделяемой для поверхностей типа Френеля, в данной работе описана ещё одна аберрация, называемая квадратичным астигматизмом. Несмотря на то, что полученные выражения являются приближением для области аберраций третьего порядка, то есть аберрации высшего порядка игнорируются, они обеспечивают достаточную точность на практике, что также показано в работе. Полученные выражения можно применять для анализа аберраций в схемах, использующих линзу Френеля, что позволяет определить области рационального использования элементов такого типа.
Коэффициенты зейделя, поверхность френеля, линейная кома, квадратичный астигматизм
Короткий адрес: https://sciup.org/140301831
IDR: 140301831 | DOI: 10.18287/2412-6179-CO-1276
Текст научной статьи Анализ аберраций третьего порядка линзы Френеля
В настоящее время линзы Френеля находят широкое применение во многих оптических устройствах, таких как концентраторы солнечной энергии, шлемы виртуальной реальности и других [1–4] благодаря высокому светопропусканию, небольшой массе, малым габаритам и низкой стоимости при массовом изготовлении [5–6].
Линзы Френеля могут обеспечить лучшее качество изображения при использовании их в системах, в том числе виртуальной и дополненной реальности по сравнению с оптическими системами с тем же количеством поверхностей, построенными на использовании классических линз. Это говорит о возможности использования таких элементов для замены обычных линз в оптических приборах с высокими требованиями к качеству изображения. При этом для анализа аберрационных возможностей оптических схем необходимо иметь математический аппарат, позволяющий описывать аберрационные свойства систем, использующих поверхности Френеля, а также анализировать их аберрационный вклад в общий баланс аберраций системы, в которой используются поверхности и элементы различного типа.
Выражения для аберраций линз Френеля, полученные на основе трассировки реальных лучей, были представлены в работах Erwin Delano [7–9]. Применение подхода трассировки лучей обеспечивает высокую точность выражений, однако не обеспечивает удобство их использования на практике, а также не дает возможности анализировать свойства таких поверхностей одновременно с обычными гладкими поверхностями. В данной работе на основе комбинации теории аберраций третьего порядка и подхода, основанного на трассировке лучей, получены выражения для аберраций линзы Френеля в приближении третьего порядка (суммы Зейделя). Также, кроме специфической аберрации, присущей таким системам – линейной коме [7], выделена новая аберрация, называемая квадратичным астигматизмом, существующая только в меридиональном сечении.
Анализ аберраций поверхности Френеля
Для анализа аберраций поверхности Френеля прежде всего рассмотрим аберрации обычной (гладкой) асферической поверхности (см. рис. 1), где I – асферическая поверхность второго порядка, III – поверхность Френеля. В данном случае бороздки рассматриваются как бесконечно узкие, а эффекты дифракции игнорируются.
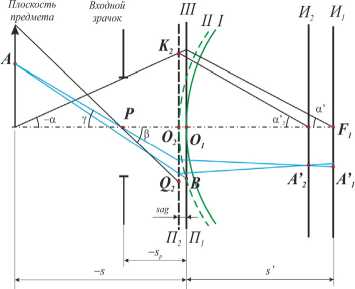
Рис. 1. К расчету аберрации поверхности Френеля:
I – поверхность второго порядка, II – поверхность, эквивалентная поверхности I, III – поверхность Френеля
Рассмотрим произвольный луч с координатами ω k , Ω k , γ k от внеосевой точки A .
Поперечные аберрации третьего порядка относи- тельно главного луча гладкой асферической поверх ности второго порядка I могут быть описаны выра жениями [10]:
8 g ' i —
to k ( to 2 + Q k ) • S 1 1 + ( 3to 2 + Q k ) -Y k • S 2 1 + to k •y 2 • [ з S 3 i + ( J л k ) 2 S 4 i ]
- 2 n ' a'
Qk (tok + Q2 ) • S11 + 2tokQkyk • S21 + QkY2 • [S3i + (J• Yk )2 S4i 1
8 G 'i ------------------------------------------------ L]
- 2 n ' a'
где S 1 I , S 2 I , S 3 I , S 4 I – коэффициенты Зейделя; J – инвариант Лагранжа; h 0 = D вх / 2 – максимальная высота луча на входном зрачке; y – максимальный линейный размер предмета; l – координата луча в плоскости предмета; ω, Ω – тангенсы угла между оптической осью и лучом, идущим из осевой точки предмета в точку на зрачке с координатами ( m , M ); to k = to /a = m / h 0 e [-1,1] - относительная зрачковая координата в меридиональном сечении, Qk ^ /a= M / h 0 e [-1,1] - относительная зрачковая координата в сагиттальном сечении, Y k =у/р= 1 / У e [-1,1] -относительная полевая координата; γ – тангенс угла между лучом от точки А до центра входного зрачка и оптической осью; α, α′ – тангенсы углов, образованных первым вспомогательным лучом с осью в пространстве предмета и изображения соответственно; β, β′ – тангенсы углов, образованных вторым вспомогательным лучом с осью в пространстве предмета и изображения соответственно; n, n′ – показатели преломления до и после преломления на поверхности I ; h 1 , H 1 – высоты первого и второго вспомогательных лучей на главных плоскостях преломляющей поверхности; sp – отрезок, определяющий положения центра диафрагмы относительно вершины поверхности (положение входного зрачка); s, s′ – отрезки, определяющие положения предмета и изображения относительно вершины поверхности.
Коэффициенты Зейделя асферической поверхности второго порядка – поверхности I – определяются формулами [11]:
Га,' аЛ
S11 — A2 • h • I a-a | + G1,
( n' n J
Г a a 1 H1
S 2 I — A 1 • B 1 • h 1 • I| + G 1 , ( n ' n ) h 1
Г a' a 1 I H 1
S 3 I — B 1 2 • h 1 • I| +I | • G 1 ,
( n ' n ) ( h 1 )
S 41 — -J2 • c • I — -11,
( n' n )
где G 1 — h 4 • c 3 •o^ n ' - n ) , A 1 = n • (- a + h 1 - c ), B 1 = n • (- P + H 1 " c ), g - коническая константа, с - кривизна поверхности при вершине ( с = 1/ r ).
Рассмотрим поверхность Френеля III . Падающий луч с координатами ω k , Ω k , γ k от внеосевой точки предмета A встречает поверхность Френеля III в некоторой точке B . Построим криволинейную поверхность II , которая описывается тем же уравнением второго порядка, что и поверхность I [12], через точку пересечения рассматриваемого луча с поверхностью Френеля. Данную поверхность будем называть эквивалентной поверхности I [12]. Пусть П 1 , П 2 – соответственно главные плоскости поверхности I и II ; A′ 2 – идеальное изображение точки A через поверхность II . Расстояние между плоскостями П 2 и П 1 можно описать выражением [13]:
sag ( to k , Q k , Y k ) “ P> k ,2 Q k , Y k ) • с + + р 4( Ю k , ^ k , Y k ) • с 3za + 1 ) , 8
где
p ( to k , Q k , Y k ) — V( h 1 •to k + H 1 •Y k ) 2 + ( h 1 •Q k ) 2
– расстояние от оси Oz до точки пересечения падающего луча и поверхности II .
Высота h 2 апертурного луча на поверхности П 2 и тангенс угла апертурного луча в пространстве изображения определяются следующими выражениями:
h 2(tok, Qk, Yk) — h1 + sag (tok, Qk, Yk) •a, a '2(tok, Qk, Yk) —
n •« + h 2 ( to k , Q k , Y k ) •Ф n '
где Φ – оптическая сила поверхности, Φ = (n′ – n)∙c , h 2 = O 2 K 2 .
Высоту H 2 главного луча на плоскости П 2 и тангенс угла главного луча в пространстве изображений можно определить аналогичными выражениями:
H 2 ( to k , Q k , Y k ) — H 1 + sag ( to k , Q k , Y k ) •P ,
x n'B + H(tot,Qk,Yk)•Ф
P '2( tok, Qk, Yk) — ——2 k ’ k, k —, n'
где H 2 = O 2 Q 2 .
Высоту главного луча, соответствующего точке А, в плоскости изображения И 1 , то есть точке A' 1 , можно описать следующим выражением:
y ' ГЛ 1 ( to k , Q k , Y k ) — F 1 A ' 1 —
H 2 ( to k , Q k , Y k ) -1 h 2 ( to k , Q k , Y k ) + d ( to k , Q k , Y k ) | •P ‘ 2 ( to k , Q k , Y k ) ( a ‘ 2 ( to k , Q k , Y k ) )
•Y k .
Таким образом, поперечные аберрации третьего порядка относительно главного луча гладкой асфери- ческой поверхности второго порядка II могут быть описаны выражениями [10]:
8 g ' 2 —
- 2 n ' a' 2 ( w k , Q k , у k )
to k ( to k + Q k ) • S 1 II ( to k , Q k , у k ) + + ( 3to k +Q 2 ) -у k • S 2 II ( to k , Q k , у k ) + +to k • у k • [ з s 3 11 ( to k , Q k , у k ) + ( J •у k ) 2 S 4 11 ]
,
8 G '2 —
- 2 n ' a' 2 ( to k , Q k , у k )
I
^ к ( to k +Q k ) • S 1 д ( ю k , Q k , у k ) + + 2to k П k у k • S 2 „ ( to k , Q k , у k ) + v ■<> k у k • [ S 3 „ + ( J •у k ) 2 S 4 „ ]
,
где
S 1 II ( to k , Q k , у k ) - A 2 ( to k , Q k , у k ) • h 2 ( to k , Q k , у k ) • I a '2( to k ’ Q k ’ у k ) --I + G 2 ( to k , Q k , у k ), V n ' n )
Xi/ x I a 2 ( to k , Q k , у k ) a I H 2 ( to k , Q k , у k ) / г-x x
S 2 II — A 2 ( to k , Q k , у k ) • B 2 ( to k , Q k , у k ) " h 2 ( to k , Q k , у k ) " I : I + ” у G 2 ( to k , Q k , у k ),
V n ' n ) h 2 ( to k , Q k , у k )
2z x I « ' 2 ( to k , Q k , у k ) a I I H 2 ( to k , Q k , у k ) I
S3II — B2 (tok , Qk , уk ) • h2 (tok , Qk , уk ) • I ----------:---I + I “2“------------ I • G2 (tok , Qk , уk ),
V n ' n ) V h 2 ( to k , Q k , у k ) )
S 4 II — S 4 1 ,
G 2 ( to k , Q k , у k ) — h 24 ( to k , Q k , у k ) • c 3 •o^ ( n '- n ) ,
A 2 ( to k , Q k , у k ) — n ( -a + h 2 ( to k , Q k , у k ) • C ) ,
B 2 ( to k , Q k , у k ) — n ( -p + H 2 ( to k , Q k , у k ) • C ) .
Поскольку положение изображения A'2 зависит от координат луча to k , Q k , y k и не находится в фиксированном положении, для удобства описания аберрации поверхности Френеля исследуются в плоскости изображения И 1 асферической поверхности [14]. Так как плоскость изображения И 2 находится на расстоянии d от плоскости И 1 , то поперечную аберрацию данного луча в плоскости И 1 можно описать формулой:
8 g ' d —8 g Vto k , Q k , у k ) +
+ d ( to k , Q k , у k ) • ( -a '2 ( to k , Q k , у k ) •to k ) , (3)
8 G ' d —8 G ' 2 + d ( to k , Q k , у k ) ( -a ’2( ra k , Q k , у k ) •Q k ) , где
. / \ hl h (tot , Qt , ук ) / \ d (tok, Qk, уk) — У 2 ; k Д 2 + sag (tok, Qk, уk).
a ' a ' 2 ( to k , Q k , у k )
С учетом описанного выше порядка расчета луча через эквивалентную поверхность и поверхность Френеля можно описать смещение положения точки главного луча в плоскости И 1 следующей формулой:
А у ' гл ( to k , Q k , у k ) — y ' ГЛ 1 (0,0, у k ) - y ' ГЛ 1 ( to k , Q k , у k ).(4)
Таким образом, выражения (2), (3), (4) дают возможность получить выражение для аберраций луча с координатами to k , Q k , y k поверхности Френеля в следующем виде:
8 g ' fres —8 g ' 2 + d ( to k , Q k , у k ) • ( -a ' 2 ( to k , Q k , у k ) •to k ) -
-А у ' гл ( to k , Q k , у k ), (5)
8 G ' fres — 8 G ' 2 + d ( to k , Q k , у k ) ( -a ’2 ( m k , Q k , у k ) •Q k ) .
Формула (5) является общей формулой для вычисления аберраций поверхности Френеля, однако на практике удобней воспользоваться приближенной формулой более простого вида, включающей в себя члены только до третьего порядка.
Таким образом, если пренебречь всеми членами, степень которых выше третьего порядка, из формулы (5) можно получить выражение:
8 g ' fres —8 g ' 1 + d ( to k , Q k , у k ) • ( -a ' 2 ( to k , Q k , у k ) •to k ) -
-А у ' гл ( to k , Q k , у k ),
8 G ' fres —8 G ' 1 + d ( to k , Q k , у k ) ( -a '2 ( to k , Q k , у k ) •Q k ) ,
где
d ( to k , Q k , у k ) • ( -a ' 2 ( to k , Q k , у k ) •to k ) —-to k x
h 1 •a•Ф n ' a '
-a+a'
(hi •tok + H1 •уk) +(h1 •Qk)
2 c
А у' гл ( to k , Q k , у k ) — 2 • [ ( h 1 •to k ) 2 + 2 h 1 H 1 to k у k +
+ (h1 •Qk )2 ] •
h1 •^•Ф n '•a'
+ P^P
•у k .
Таким образом, аберрации третьего порядка поверхности Френеля описываются выражениями:
8 g ' fres =8 g ' 1 - ® k •
hi • a • Ф n' a'
a + a'
(hi•®k+ Hi •yk) + (hi -Q k)
2 с
-2 • [(hi • ®k )2 + 2hiH1®kyk + (hi • Qk )2 ] •
8 G'fres = 8 G 'i - Qk •
hi • a • Ф n' a'
-a + a'
-
h'Р'Ф n. nl
, , + P ' -P •Y k , n ' •a '
( h i •w k + H i •y k ) 2 + ( h i •Q k ) 2 2
Для удобства представления формул обозначим:
a =
h • a • Ф
--a + a n' a'
hi • Pi • Ф n '•a'
+ P '-P.
Тогда выражение (6) можно переписать в виде:
8g'fres = 8g'i + ^[®k (®2 + Q2) • hi2 • a + Yk (3®k + Qk) • a • hi • Hi + Yk®k • 3Hi2 • a] +
+ ^ C - [ Y k ( ® 2 +Q k ) • h i • ( b • h i - a • H i ) ] ' 2'' [Y 2 ® k • 2 H i • ( b • h i - a • H i ) ] , (7)
8 G ' fres = 8 G ' i - 2’ ' [Q k ( ® 2 + Q 2 ) • h i 2 • a + 2 ® k Q k Y k • a • h i • H i + Y k Q k • H i 2 • a ] ■
При сравнении членов в формуле (7) с известными коэффициентами Зейделя можно заметить, что в формуле поперечной аберрации в меридиональном сечении есть два члена, которых нет в выражении для стандартной гладкой поверхности. Первый член – линейная кома, которая линейно пропорциональна величине предмета, зависит от квадрата величины зрачка и не зависит от положения зрачка. Вторая составляющая, которая отсутствует для стандартных поверхностей, – квадратичный астигматизм, который пропорционален квадрату величины предмета, а также линейно пропорционален положению и величине зрачка. Полученные выражения дают возможность оценить аберрации оптической системы, в которой используются поверхности Френеля.
Таким образом, коэффициенты Зейделя поверхности Френеля определяются формулами:
S i fres = S i I + n '•a ' • c • h i; • a ,
S 2 fres = S 2 I + n ' • c •a ' • h i • H i • a ,
S 3 fres = S 3 I + n ' • c •a ' • H 2 • a ,
S 4 fres = S 41 , line _ coma = -с- [ Yk (®2 +Q2 )• hi •( b • hi - a • Hi)], square _ ASTI = -с- [Y2®k • 2Hi • (b • hi - a • Hi)].
Если предмет находится на бесконечно большом расстоянии, то a = α′, b = β′, в этом случае выражения для коэффициентов Зейделя принимают вид:
S i f res = S i I + n '•a '2 • c • h i 2,
S 2 fres = S 2 I + n ' • c •a '2 • h i • H i;
S 3 fres = S 3 I + n ' c •a '2 • H i2 ,
S 4 fres = S 41 , line coma = —с^-
Q k ) • h i •₽• D • n , 2 n '
square _ ASTI = -с- y k ® k • 2 • sp •P 2 • D • — 2 2 n '
Таким образом, теоретический анализ показал наличие специфических для поверхности Френеля аберраций, в частности комы, которая не зависит от положения зрачка, а также астигматизма, который линейно зависит от положения зрачка.
Верификация и математическое моделирование
На рис. 2 показан результат сравнения поперечной аберрации в меридиональном сечении при применении формулы (7) и при трассировке реальных лучей с помощью программы Zemax. Конструктивные параметры системы, для которой выполнен расчет: n = 1, n ′ = 1,5, Dвх = 10, s = ∞, sp =– 8 мм, r =20 мм, угловое поле в пространстве предметов 2ω =4°, коническая константа σ =–3.
Из рисунка видно, что поперечные аберрации для осевой и внеосевой точки предмета при расчете и при трассировке реальных лучей отличаются незначительно: для данного случая максимальная разница составила не более 9,5 %. Таким образом, полученные выражения могут быть полезны при анализе систем с поверхностями Френеля, а также позволяют оценить влияние поверхности Френеля на баланс аберраций в системе и на качество изображения.
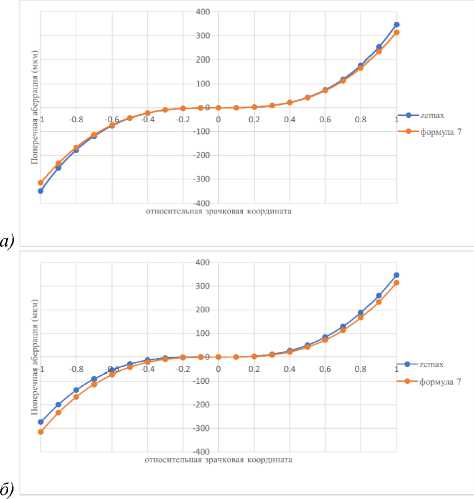
Рис. 2. Поперечные аберрации поверхности Френеля, рассчитанные по полученным формулам (7) и путем трассировки в Zemax: a) для осевого пучка, б) для внеосевого пучка
Заключение
В работе получены выражения для аберраций третьего порядка для поверхности Френеля. Полученные выражения позволили показать, что для таких поверхностей характерно наличие специфических аберраций, в том числе линейной комы, которая не зависит от положения зрачка, а также квадратичного астигматизма, линейно зависящего от положения зрачка. Полученные формулы для аберраций поверхности Френеля обеспечивают достаточную точность вычислений и могут применяться для анализа абер- раций в разнообразных схемах, использующих линзы Френеля.
Список литературы Анализ аберраций третьего порядка линзы Френеля
- Romanova GE, Nguyen NS. Aberration analysis of decen-tered lenses for the compensation of vergence-accommodation conflict in virtual reality systems. J Opt Technol 2022; 89: 517-523.
- Brian W, Jacques G, Melissa G. Hybrid fresnel lens with reduced artifacts. US Patent 10133076B2. 2018.
- Xie WT, Dai YJ, Wang RZ, Sumathy K. Concentrated solar energy applications using Fresnel lenses: A review. Renew Sust Energ Rev 2011; 15(6): 2588-2606.
- Leutz R, Suzuki A, Akisawa A, Kashiwagi T. Developments and designs of solar engineering Fresnel lenses. China Proc Symp on Energy Engineering (SEE 2000) 2000; 2: 759-765.
- Bang K, Jo Y, Chae M, et al. Lenslet VR: Thin, flat and Wide-FOV virtual reality display using fresnel lens and lenslet array. IEEE Transactions on Visualization and Computer Graphics 2021: PP(99):1-1.
- Greisukh GI, Stepanov SA, Antonov AI. Comparative analysis of the fresnel lens and the kinoform lens. Computer Optics 2018; 42(3): 369-376. DOI: 10.18287/2412-6179-2018- 42-3-369-376.
- Delano E. Primary aberrations of Fresnel lenses. J Opt Soc. Am 1974; 64: 459-468.
- Delano E. Primary aberrations of meniscus Fresnel lenses. J Opt Soc Am 1976; 66: 1317-1320.
- Delano E. Primary aberration contributions for curved Fresnel surfaces. J Opt Soc Am 1978; 68: 1306-1309.
- Slyusarev GG, Methods of calculating optical systems [In Russian]. Moscow: "Mashinostroenie" Publisher; 1969.
- Hopkins HH. Wave theory of aberrations. New York: Oxford University Press; 1950.
- Jing LC. Ray tracing of Fresnel systems. Appl Opt 1983; 22: 560-562.
- Bobrov ST, Greisukh GI, TurkevichYuG. Optics of diffraction elements and systems [In Russian]. Leningrad: "Mashinostroenie" Publisher; 1986.
- Zemax Optic Studio 19.8 User manual. October 2019.


