Анализ алгоритма кодирования аудио волны на основе спектрограмм

Цель работы – количественная и визуальная оценка изменений в аудио сигнале после использования алгоритма кодирования аудио волны (АКАВ).

В работах ( Лейтес, Соболев , 1969; Соболев , 2006) был предложен алгоритм кодирования речевой волны (АКРВ). Авторы алгоритма утверждали, что восстановленный после кодирования речевой сигнал имеет приемлемую разборчивость при прослушивании. Мы использовали данный алгоритм в системе распознавания изолированных слов русского языка для формирования признаков. Тестирование различных вариантов алгоритма показало изменение разборчивости анализируемого сигнала в широком диапазоне. Результаты распознавания кодированных фрагментов давали также различную точность распознавания. Эти результаты потребовали от нас более тщательного математического анализа АКРВ. В силу того, что мы стали применять этот алгоритм к различным аудио сигналам, мы перешли от авторского названия алгоритма кодирования речевой волны к АКАВ.

В данной работе коротко излагаются алгоритмы кодирования аудио сигнала и обратного восстановления на основе АКАВ. После этого описывается алгоритм распознавания ( Жарких, Павлов , 2008; Павлов, Жарких , 2007), основанный на параметрах кода аудио волны. Далее приведены результаты сравнения исходных аудио сигналов с аудио сигналами, преобразованными алгоритмами кодирования и восстановления на основе АКАВ. Сравнение проводится во временной, частотной и частотно-временной областях.

вектор модулей ординат глобальных экстремумов y = ( y 1 , y 2 ,…, y j , …, y J ), где y j = max | x n | на j -ом интервале постоянного знака аудио волны; вектор разностей абсцисс соседних глобальных экстремумов t = ( t 1 , t 2 ,…, t j , …, t J ), где t j = arg y j – arg y j -1 (величины t j выражаются в количестве шагов дискретизации кодируемого аудио сигнала). Совокупность двух указанных векторов является компактным описанием аудио волны, которая может быть восстановлена по правилу ( Соболев , 2006):

-    (-1)j-1 ■ j + (-1)j- yj ( x n =-----------------------+ (-1) j 1

y j - 1 ⁺ y j ■

П ■ cos(— ■ i ), t_j

где i = 1 ..t j , j = 1 ..J . Таким образом, для каждого аудио сигнала получается вектор информативных признаков: ( y 1 , y 2 ,…, y J , t 1 , t 2 ,…, t J ), состоящий из 2 J компонент. Эти признаки в дальнейшем используются при распознавании сигналов. АКАВ применялся совместно с низкочастотной Фурье-фильтрацией ( Гольденберг и др. , 1990), что позволило гибко управлять размером вектора информативных признаков.

• 3.    Алгоритм распознавания аудио сигнала на основе АКАВ признаков

  Для распознавания аудио сигналов использовался метод сравнения с эталонами с последующим нахождением степени сходства с эталонами. Степень сходства между аудио записями и эталонами рассчитывалась на основе алгоритма динамического программирования ( Рабинер, Шафер , 1981).

На вход алгоритма подавались входной и эталонный векторы информативных признаков: (y1, y2,…, yi ,…, yM, t1, t2 ,…, ti ,…, tM), (Y1, Y2,…, Yj ,…, YN, T1, T2,…, Tj ,…, TN). Алгоритм дает возможность найти функции fy и fY , позволяющие для любого элемента входного вектора признаков найти соответствующий ему элемент эталонного вектора признаков. На основе данного алгоритма определялась степень сходства входного и эталонного векторов признаков.

Степень сходства между парами ( y i , t i ) и ( Y j , T j ) рассчитывалась по формуле:

R ij =

' m^in{ y i , Y j }

■ ®1

max{ y i , Y j } V             j

min{ t_i , T_j }

+--- to 2

max{ t_i , T_j }

/(to! + to2 ), J

где i = 1,…, M ; j = 1,…, N ; ω ₁, ω ₂ – весовые коэффициенты, ω ₁ + ω ₂ = 1.

Алгоритм распознавания показал различную степень правильного распознавания изолированных слов русского текста. Если использовались дополнительные фильтры, то степень распознавания изменялась от 50 до 97 процентов. При кодировании АКАВ разборчивость аудио сигнала как правило ухудшалась. Однако прямой корреляции между ухудшением качества распознавания и ухудшением разборчивости при прослушивании не наблюдалось. То есть были варианты приемлемые при прослушивании и хорошие по распознаванию, но были и варианты плохие при прослушивании и хорошие при распознавании. Это и привело авторов к необходимости тщательного математического анализа результатов применения АКАВ.

представляет собой объединение амплитудных спектров, вычисленных на коротких сегментах, в функцию двух переменных или матрицу.

Согласно многим источникам и самостоятельным экспериментам авторов, амплитудный спектр плохо представляется в линейном масштабе. Это плохое представление характерно как для кратковременного преобразования Фурье, так и для преобразования Фурье на более длинных реализациях. Это связано с тремя обстоятельствами: с особенностью человеческого зрения (ограниченная разрешающая способность и нелинейное восприятие изображения), с особенностями представления изображений и графиков на компьютере, а также с конкретными значениями амплитудных спектров, возникающих в процессе вычисления. Если преобразование Фурье осуществляется на длинных отрезках записи, то типичной является ситуация, когда несколько низкочастотных составляющих имеют очень большое значение, а большое количество (70-85 %) более высокочастотных составляющих имеют существенно меньшие значения и представляются как будто бы шумом. При этом отличие между максимальным значением низкочастотной составляющей и более высокочастотной составляющей может составлять несколько десятков порядков. Если преобразование Фурье осуществляется на коротких промежутках, то возможна ситуация, когда амплитудный спектр имеет некий шумоподобный характер. Выделить вклад определенных гармоник оказывается очень сложно. В частности, при сборке кратковременных амплитудных спектров в спектрограмму проявляется только часть спектральных составляющих, а б о льшая часть теряется.

Традиционно для визуализации амплитудного спектра аудио сигнала и спектрограммы, в частности, используется логарифмическая шкала в децибелах:

S ( k ) = 20 • log io IX ( k )|,                                                  (3)

где k = 0,…, N -1, N – количество отсчетов в спектре, | X ( k )| – k -е значение отчета амплитудного спектра исходного сигнала, S ( k ) – результирующее значение отчета амплитудного спектра. Однако эта шкала, на взгляд авторов, является неудобной, т.к. в ней неправильно обрабатываются нулевые значения амплитуд. Если значение амплитуды становится близким к нулю, но положительным, то в логарифмической шкале это соответствует большому отрицательному значению. Минимальное значение амплитуды, которое можно представить в шкале децибел, не нарушив физического смысла, равно 1.

Авторы используют альтернативный способ визуализации амплитудного спектра и спектрограммы, в частности, в работах ( Жарких, Коннов , 2007; Zharkikh, Pavlov , 2008). Визуализация спектрограммы проводится на основе функции гиперболического тангенса и представлена формулой:

A ( r , k ) = [ 255 • th ( a J ^x r ( k )|) ] ,                                             (4)

где | X r ( k )| – k -е значение отсчета амплитудного спектра сегмента r , α – параметр для управления визуализацией, A ( r , k ) – значение пикселя изображения спектрограммы, хранящейся в виде матрицы, в которой r – индекс столбца, соответствующий диапазону временной шкалы t_r = 0, RT , 2 RT ,…, ( N_R- 1) RT спектрограммы и k – индекс строки, соответствующий диапазону частотной шкалы F_k = kF_s/N , k = 0, 1, …, N/ 2 спектрограммы, T – период дискретизации сигнала, F s – частота дискретизации сигнала. В выражении (4) кратковременное преобразование Фурье вычисляется согласно формуле ( Rabiner, Schafer , 2009):

rR + L - 1

X r ( k ) =

X

m = rR

x ( m ) w ( rR - m ) e

2”ь

— j—km N

где L – размер сегмента (в отсчетах), N – количество дискретных отсчетов, используемых для вычисления быстрого преобразования Фурье (БПФ), w ( m ) – окно, используемое для вычисления кратковременного преобразования Фурье, N_R – количество сегментов, на которые разбивается сигнал, R – смещение сегмента (в отсчетах).

Множитель 255 выбран из тех соображений, чтобы все значения амплитудного спектра были представлены на картинке в градациях серого. К сожалению, авторы пока не разработали методику оптимального подбора параметра α и подбирают его в процессе вычисления.

Функция гиперболического тангенса преобразует интервал [0; +∞) в интервал [0; 1), поэтому любые значения амплитуды будут отображены на рисунке спектрограммы. Кроме этого, рисунок является более качественным и контрастным, чем это позволяет сделать шкала децибел. Авторы предполагают и дальше разрабатывать эту методику визуализации, т.к. результаты ( Жарких, Коннов , 2007; Zharkikh, Pavlov , 2008) и данной работы показывают, что такая визуализация позволяет выявить некоторые детали и особенности спектра, что не всегда позволяют сделать другие средства.

При моделировании использовались следующие значения параметров аудио сигналов и параметров вычисления спектрограммы:

(а)

(б)

(в)

(г)

(а)

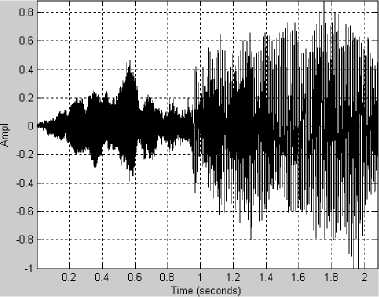
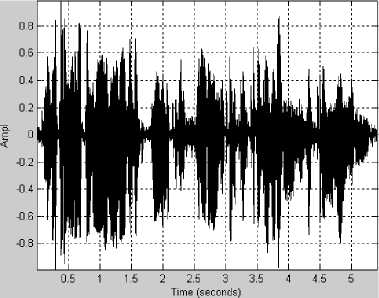
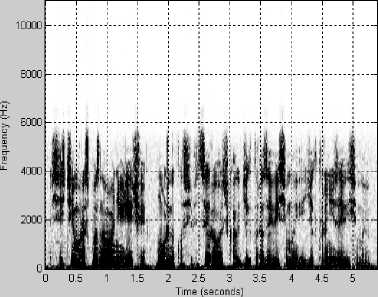
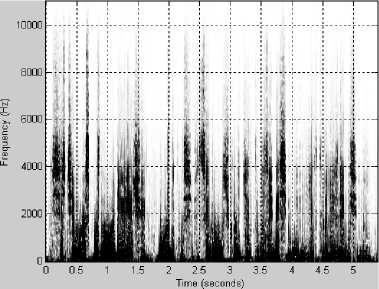
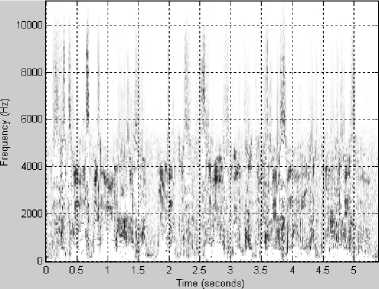
Рис. 1. Фрагмент речевого сигнала, соответствующий фразе, произнесенной одним из авторов

(б)

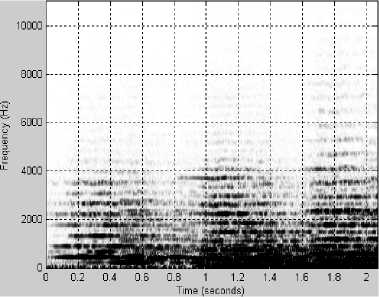
(в)

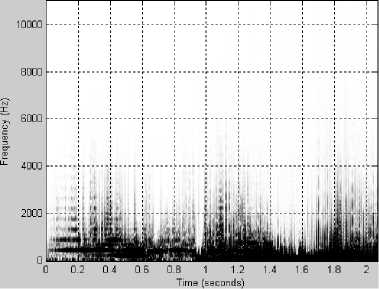
(г)

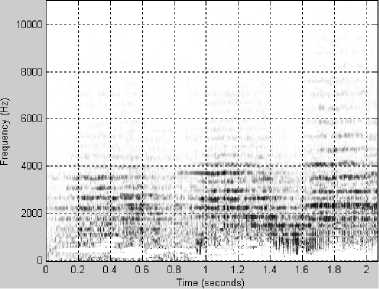
Рис. 2. Фрагмент классической музыки, соответствующий музыкальному произведению "Менуэт", композитор Вольфганг Амадей Моцарт

(а)

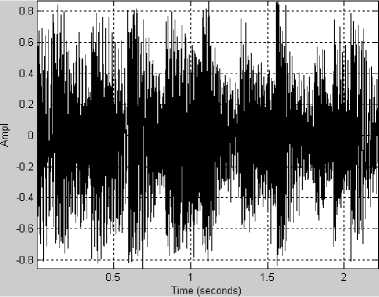
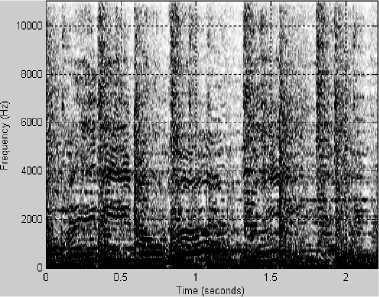
(в)

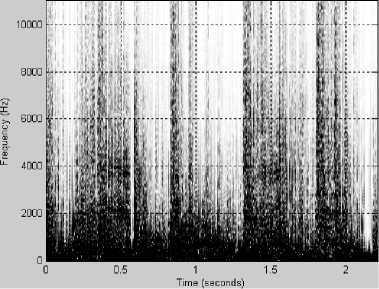
(г)

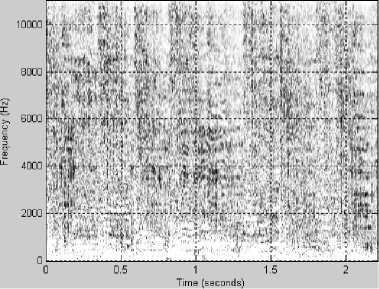
Рис. 3. Фрагмент современной музыки, соответствующий песне "What Is Love" музыканта Haddaway

• •    Формат аудио сигнала: PCM WAV;

• •    Частота дискретизации ( F s ): 22050 Гц;

• •    Число уровней квантования (разрядность): 16 бит;

• •    Окно ( w(n) ): окно Хэмминга;

• •    Размер сегмента ( L ): 512 отсчетов (23 мс);

• •    Смещение сегмента ( R ): 170 отсчетов (8 мс);

• •    Перекрытие сегментов ( L-R ): 342 отсчета (15 мс);

• •    Размер БПФ ( N ): 512 отсчетов (23 мс);

• •    Параметр для управления визуализацией ( α ): 1 .

Для удобства сравнения исходного сигнала и восстановленного после АКАВ строилось изображение разности спектрограмм этих сигналов. Для амплитуд спектрограмм A ₁( r , k ) и A ₂( r , k ) изображение разности строилось с использованием формулы:

A ₃( r , k ) = A ₁( r , k ) - A ₂( r , k ) .                                                 (6)

Несколько характерных примеров спектрограмм приведены на рис. 1-3. На всех рисунках: график (а) – исходный сигнал, график (б) – спектрограмма исходного сигнала, график (в) – спектрограмма сигнала, восстановленного после АКАВ, график (г) – разность спектрограмм исходного сигнала и восстановленного после АКАВ.

Кроме этого проводились следующие оценки, которые осуществлялись на основе метрики L2:

• •    Нормированное расстояние между исходным и восстановленным после АКАВ сигналом:

ρ ( x , y ) = II x - y II /(II ^x II + II ^y II),                                                           (7)

в выражении (5)

N - 1

II ^x II = ∑ x m ²

где N – количество временных отсчетов, x_m – значение отчета исходного сигнала, y_m – значение отчета сигнала, восстановленного после АКАВ. Аналогичным образом рассчитывались || y || и || x-y ||.

• •    Коэффициент корреляции во временной области между исходным и восстановленным после АКАВ сигналом:

k ( x , y ) = ( x , y ) /(II ^x II ^⋅ II y II),                                                                         (8)

в выражении (6)                              N - 1

( x , y ) = ∑ x_m ⋅ y_m .

m = 0

• •    Коэффициент корреляции в частотной области между исходным и восстановленным после АКАВ сигналом:

• 5.    Заключение

N - 1

K ( X , Y ) = Re( ∑ X m ⋅ Y m )/(II ^X II ^⋅ II ^Y II) .                                            (9)

m = 0

Результаты анализа АКАВ позволяют сделать следующие выводы:

• 1)    Сигнал, полученный в результате кодирования на основе АКАВ, требует для хранения объем памяти в 4-5 раз меньше, чем исходный сигнал.

• 2)    Во всех случаях действие АКАВ эквивалентно пропусканию сигнала через фильтр нижних частот.

• 3)    Во многих случаях применение АКАВ приводит также к режекции средней части спектра в области нижних частот.

• 4)    Нормированное расстояние между исходным и восстановленным после АКАВ сигналом для аудио сигналов различного класса составляет приблизительно 0.22-0.5.

• 5)    Коэффициент корреляции во временной области между исходным и восстановленным после АКАВ сигналом для различных типов аудио сигналов изменяется от 0.5 до 0.92.

• 6)    Коэффициент корреляции в частотной области между исходным и восстановленным после АКАВ сигналом для различных типов аудио сигналов изменяется от -0.24 до 0.35. Такие маленькие величины связаны с изменением фазы в восстановленном сигнале и интерференцией сигналов при вычислении коэффициента корреляции.

• 7)    Анализируя графики разности спектрограмм исходного сигнала и восстановленного после АКАВ, можно сделать вывод, что для всех трех вариантов образцов лучше всего сохраняется частотный диапазон 0-1000 Гц.