Анализ алгоритмов реализации VPN с совместными ограничениями по задержке и полосе пропускания

Технология виртуальных частных сетей VPN (Virtual Private Network)позволяет превратить соединения в пакетных сетях общего пользования в защищенные каналы с гарантированной полосой пропускания [1].VPNобеспечивает безопасность и секретность как в традиционной частной сети при сохранении стоимости устанавливаемых соединений как в сети общего пользования.Большая часть выполненных в последние годы теоретических исследований VPN была посвящена проблемам оптимизации величины полосы пропускания,резервируемой в сети общего пользования для реализации виртуальной сети [1; 3]. Однако лишь немногие работы затрагивают проблемы обеспечения в VPNзаданных ограничений качества обслуживания трафика QoS (Quality of Serviсe).Одной из таких проблем является задача поиска пути в графе с наименьшей стоимостью и наименьшей задержкой LCLD (Least Coast Least Delay).Вместо параметра «стоимость» при решении задачи можно использовать параметр«полоса пропускания»,так какони чащевсе-го связаны линейной зависимостью.

Сложность теоретической проблемы решения задачи LCLD заключается в том,что не удается найти эффективные алгоритмы оптимизации,которые бы учитывали одновременно ограничения по полосе пропускания и задержке в сети.Обусловлено это тем, что данная задача оптимизации на нагруженных графах относится к классу труднорешаемых (NP-hard)[2] и ее решение возможно только аппроксимационными или эвристическими методами.В статье приведены результаты анализа имеющихся подходов к решению данной задачи и сформулировано направление дальнейших исследований.

Алгоритм одноадресной маршрутизации трафика с ограничением по задержке DCUR

В [4]авторы предлагают распределенное эвристическое решение в виде алгоритма одноадресной маршрутизации трафика с ограничением по задерж-кеDCUR(Delay-ConstrainedUnicastRouting),которое является частным случаем решения задачи LCLD.

Алгоритм DCUR определяет путь в графе сети, соединяющий узел-отправитель s с узлом-получателем d , с выполнением заданного ограничения на задержку.Путь в графе строится последовательно от исходного узла-отправителя к узлу-получателю. В общем случае от любого узла v в маршруте до узла-получателя d можно добавить в путь одно из двух альтернативных звеньев сети.Одно звено сети входит в состав пути с наименьшей стоимостью (полосой пропускания)(назван как LC-путь),в то время как другое звено входит в путь с наименьшей задержкой (назван как LD-путь).В частном случае возможно использование только одного звена, если исходящие из узла v LC-путь и LD-путь совпадают.

Такое ограничение в выборе каждого следующего звена е в пути Pi значительно уменьшает объем вычислений, выполняемых в каждом узле i. Для реализации алгоритма DCUR в каждом узле необходимаследующаяинформация:информация о том, какие узлы сети являются смежными для данного узла, величина полосы пропускания каждого смежного звена C(e) и задержка в этом звене D(e). Резервируемая полоса пропускания пути Pi и величина задержки на этом пути определяются выражениями С(Р) = ^С(е) и D(P) = ^D(e) ееР                      ееР соответственно. Задача выбора оптимального пути между заданными конечными точками VPN решается путем минимизации стоимости (суммарной полосы пропускания) пути min С(Р) р^р'^.л при удовлетворении неравенства D(P) < А, где А – некоторое заданное граничное значение задержки. В каждый момент времени определенный узел сети становится активным, и для него осуществляется поиск звеньев дальнейшего пути с учетом непревышения заданных порогов задержки . Если такой путь существует и выполняется неравенство d (s,d) < А , то данный узел передает информацию о выбранном пути следующему узлу, который становится активным. Таким образом, маршрут строится последовательно от узла-источника до узла-получателя с определенным разрешенным порогом задержки А . При этом на каждом шаге алгоритма меняется запись в таблице маршрутизации активного узла. Если ал- горитм не может найти путь, удовлетворяющий требованию по задержке, то поиск прекращается и алгоритм возвращает отказ с указанием невозможности создания пути с заданными требованиями. Кроме того, алгоритм предотвращает появление петель при создании пути от источника до получателя. Алгоритм DCUR рассматривает только одноадресную маршрутизацию с ограничением по задержке, причем с увеличением числа узлов в сети увеличивается объем хранимой информации в активных узлах, что приведет к дополнительным вычислительным затратам на сортировку и выдачу адресной информации соседним узлам.

Алгоритм k-кратчайших путей kSP

В [5] предлагается другой подход к решению задачи LCLD. Используется алгоритм k -кратчай-ших путей kSP ( kShortest Paths ), который позволяет строить путь в графе от узла-отправителя до узла-получателя и использует больше параметров, чем алгоритм DCUR. На основе данного алгоритма предложены следующие его модификации:

• -    алгоритм k -линейной агрегированной метрики kLAM ( k -Linearly Aggregated Metric). Вводится некоторая граничная функция B ( λ ), которая связана с функцией Лагранжа L ( λ ) неравенством ЦЛ) < в^ . Поэтому максимизация функции B ( λ ) дает лучшую нижнюю границу для оптимального пути. Алгоритм kLAM основывается на алгоритме Дейкстры и выигрывает у других подобных, например, LARAC (Lagrange relaxation based method), который использует для расчета полосы пропускания Лагранжевые релаксации. Авторы доказывают эффективность полученных решений на практических примерах с использованием в расчетах конкретных топологий графов;

• -    алгоритм Беллмана-Форда с k -ым ограничением задержки kDCBF (k-Delay-Constrained Bellman-Ford). В данном алгоритме для каждого узла u определяется два кратчайших пути: с минимальной полосой пропускания и с минимальной задержкой. Имея данные об узле-получателе, алгоритм определяет суммарную задержку, вычисляет суммарную полосу пропускания для каждого пути и находит подходящий путь, удовлетворяющий заданным ограничениям. Для каждого узла u выбираемого пути производится проверка ограничений на задержку на основании следующего неравенства:

d(s,u) + d(l ) + d (u,v) < A , где d (s,u)–суммарнаязадержканапутиотузла-отпра-вителя s до некоторого промежуточного узла u в сети;

d ( l_LC )– задержка на звене пути с наименьшей полосой пропускания (LC) l_LC = ( u , v )от узла u до смежного узла v ; d_LD ( v , d )– задержка на пути с наименьшей задержкой (LD)от узла v до узла-получателя d .

Если неравенство выполняется, то путь от s до d существует и достижим. В противном случае такой путь, удовлетворяющий ограничению по задержке Δ _d ,не может быть найден.Временная сложность алгоритма определяется выражением O^jC^ + k^. log k.. + k_d log k_d)mn) , где k_d – количество кратчайших путей по задержке от промежуточного узла u до узла-получателя d ; k_c – количество кратчайшихпутейпополосе пропусканияотузла-от-правителя s до промежуточного узла u ; n и m – число вершин и число ребер в графе сети соответственно.

Рассмотренные алгоритмы являются эффективными при правильно подобранном коэффициенте k для определенных топологий VPN.Приведены соображения,по которым выбирается параметр k . Хотя алгоритм выполняется за полиноминальное время, с увеличением значения коэффициента k поиск оптимальных путей становится трудным.Фак-тически в работе представлен алгоритм поиска оптимального пути от источника до получателя лишь с одним критерием (ограничение по задержке).

Алгоритм маршрутизации, основанный на критических звеньях LCBR

В [6]рассмотрена проблема поиска основных и резервных маршрутов передачи трафика VPN,кото-рые удовлетворяют заданным ограничениям на полосу пропускания и суммарные задержки. Для этого предлагаетсяиспользоватьалгоритммаршрутизации, основанный на использовании параметра критичности звеньев LCBR (Link Criticality Based Routing).

В работе вводится понятие критичности звена, которая сопоставляется с его динамической полосой пропускания, величина которой c ( e ) определяется как c(e) =    , где R _e – свободная полоса

R пропускания звена е; Фе – ожидаемая нагрузка на звено е.

Тогда суммарная доступная полоса пропускания в сети G вычисляется по формуле

C(G^Y.^~^ ■

Показана невозможность применения классического алгоритма Дейкстра для поиска кратчайшего пути при одновременном удовлетворении ограничений по полосе пропускания и задержке. Каждому звену e присвоен диапазон задержек для потока FN между отправителем и получателем в зависимости от величины полосы пропус- кания, выделенной для потока FN на звене e. При этом необходимо вести мониторинг загрузки сети и предотвращать перегрузки звеньев. Алгоритм LCBR основан на алгоритмах k-кратчайших путей с обратной связью и без нее и обеспечивает высокую степень распределения нагрузки и эффективность использования ресурсов сети. По сравнению с аналогичными алгоритмами, например, поиска кратчайшего пути в ширину (WSP) или минимального перекрытия маршрутов (MIRA), алгоритм LCBR является более эффективным. Он обеспечивает более низкое значение величины C(G) для длинных путей. Однако в работе делается упор на резервирование каналов и эффективное распределение полосы пропускания, требования по задержке рассматриваются как второстепенная задача.

Сведение проблемы реализации VPN к задаче выбора топологии, емкости и назначения потоков в сети CFA

В [7] задача оптимальной реализации VPN рассматривается как задача выбора топологии, емкости и назначения потоков CFA (Topology, Capacity and Flow Assignment). Для этого вместо традиционных систем массового обслуживания (СМО) с очередями (M/M/1, M/M/1/B) предлагается использовать пуассоновскую модель с групповым поступлением заявок (M_|X|/M/1). В данной модели размер группы пакетов во входном потоке изменяется от 1 до w c распределением |X|, где w – максимальный размер TCP-сессии. Тогда средняя задержка трафика в узле (с учетом времени ожидания в очереди и времени обработки в узле) рассчитывается по формуле П=ж)=--Л

X 1-р где р – коэффициент загрузки СМО; X – интенсивность поступления нагрузки (в битах/С);

2<

где ^П1'\х\ ^{и 111} – первый и второй начальные моменты распределения длины группы пакетов |X|. В [7] задача определения оптимальной топологии VPN с учетом минимизации стоимости полосы пропускания на звеньях сети сформулирована в виде задачи CFA:

Zm =min^g,z(C),

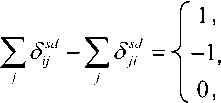
если s = i;

если d = i;

в остальных случаях;

К. У —— <КТТ,-К,У 5 ^я'd ; V(s, d^;

1 “loss

0<^Nd,j,s,d\ ^>^>0; V(/,y), где ^U ^^U ^ – стоимость полосы пропускания в звене (i, j) пути; 5^ – вспомогательная переменная (доля трафика, передаваемого по звену (i, j) от узла-источника s до узла-получателя d); Cy – пропускная способность звена (i, j); Jij – средняя нагрузка в звене (i, j); у – среднее значение пакетных данных, переданных от s до d; R TT^d – время передачи пакета по каналу (s, d); ^loss – доля потерянных пакетов; К, и К, – постоянные переменные, преобразующие расстояние во время.

Так как узлы VPN передают в сеть разнородный трафик, достаточно трудно вычислить оптимальный путь для каждой пары узлов «отправитель-получатель» и конкретного типа трафика. С математической точки зрения, в вышеуказанном уравнении имеются нелинейные ограничения. Для его решения применен метод Лагранжевых релаксаций. При замене переменных и несложных преобразованиях получается эквивалентная задача оптимизации в виде

ZCFA = min[£ ^ + У У d^ysd ], где ^0 – физическая длина звена (i, j);

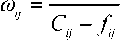
Решения в этом случае могут быть получены при использовании Лагранжевых релаксаций. Формулируется задача Лагранжа, разрешимая за полиномиальное время

Ца, /3) = Ц (a, /3) + L, (a, /3}, где α и β – множители Лагранжа, LA«,P^ и LAa,p^ – отдельные задачи.

В свою очередь, задача P(«,P) делится на 77(77-1) задач поиска кратчайшего пути (одного для каждой пары отправитель/получатель), которые находятся с использованием классического алгоритма Беллмана-Форда. Задача LA«,P^ решается путем разбиения на m независимых подзадач.

В [7] приведены примеры использования метода для графов сетей с разным количеством узлов. Результаты исследования показали, что данный метод обеспечивает весьма эффективный подход для получения оптимальных решений. Временная сложность алгоритма определяется выражением О(пт), поэтому определение оптимальных путей при большом числе узлов сети n требует больших вычислительных затрат. Кроме того, предложенный алгоритм не учитывает особенностей потоковой модели VPN.

Алгоритм построения дерева Штейнера с минимальным диаметром (MDStT)

В [8] выполнено исследование потоковой модели с учетом ограничений по задержке передачи трафика между конечными точками VPN. Использованы три подхода для определения оптимальной топологии виртуальной сети: «сеть каналов», «деревья, образованные от нескольких источников» и «общее дерево». В подходе «сеть каналов» для каждой пары конечных точек VPN формируется свой путь в графе сети и для минимизации полосы пропускания применяется алгоритм Беллмана-Форда с учетом ограничений CBF (Constrained Bellman-Ford), при этом общая полоса пропускания определяется простым суммированием полос пропускания всех звеньев пути (аналогично канальной модели). В двух последних моделях используются древовидные топологии виртуальной сети, а значит, весь трафик из одной конечной точки VPN в другую передается по единственному пути. В этом случае суммарная полоса пропускания для реализации VPN с древовидной топологией рассчитывается по формуле Ст=Х1.,,уСАи^’ где СДи^ – полоса пропускания, резервируемая на ветви (u, v) дерева T [1; 8]. Используя теоретический анализ и результаты моделирования, авторы пришли к выводу, что подход «общее дерево» имеет преимущества перед другими, так как он обеспечивает более низкую суммарную полосу пропускания и простоту маршрутизации трафика и восстановления топологии при отказах звеньев. Для построения древовидной топологи VPN был предложен алгоритм построения дерева Штейнера с минимальным диаметром MDStT (Minimum Diameter Steiner Tree). Диаметр дерева Штейнера D определяется как максимальная задержка между любыми двумя конечными точками VPN. Авторами было доказано, что задача MDStT эквивалентна задаче определения абсолютного набора вершин графа с одним центром AS1CP(Absolute Subset 1– Center Problem). Абсолютный набор вершин с одним центром для графа G = (V,E) относительно некоторого набора вершин РсУ характеризуется вершиной графа x, для которой расстояние от нее до любой вершины из набора P минимально. Для снижения величины требуемой полосы пропускания было предложено использовать 4 вида дерева, однако рассматривается наиболее подходящее дерево с наименьшей полосой и наименьшей задержкой (задача LCLD). Для этого дерева

D граничное значение по задержке: D_shared = — , где D

– расстояние от центрального узла до конеч- 2

ной точки. Полученное дерево имеет небольшое значение резервируемой полосы пропускания, однако метод LCLD, который основывается на минимальном количестве сетевых звеньев в пути, не всегда эффективен. В некоторых случаях он просто не сможет найти все пути до заданных конечных точек.

Алгоритм общего дерева с оптимальной полосой пропускания и ограничением по задержке OBDST

В [9] авторы решают проблему поиска оптимального с точки зрения полосы пропускания общего дерева, удовлетворяющего также требованиям по задержке OBDST (Optimal Bandwidth and Delay-constrained Shared Tree). Метод основан на определении двух общих древовидных путей, один из которых удовлетворяет требованию по задержке, а другой имеет наименьшую требуемую полосу пропускания.

Алгоритм включает в себя несколько стадий. На первой стадии используется модификационный алгоритм построения дерева Штейнера (MDStT), основанный на задаче абсолютного набора вершин графа с одним центром. Если наборов с одним центром, удовлетворяющих ограничению по задержке, несколько, в отличие от подхода LCLD [8] все они рассматриваются как кандидаты для определения абсолютного центра в графе. Для каждого набора определяется дерево Штейнера, соединяющее конечные точки VPN. Полученный набор деревьев назван оптимальным общим деревом с ограничением по задержке ODST (Optimal Delay-constrained Shared Tree). Все отдельные деревья в этом общем дереве удовлетворяют ограничению по задержке, но не обеспечивают минимум полосы пропускания. На следующей стадии рассматривается алгоритм иерархического итеративного покрывающего дерева HIST (Hierarchical Iterative Spanning Tree), который определяет оптимальную полосу пропускания дерева, а также вводится схема ранжирования, учитывающая требования пользователей. Для каждого отдельного дерева T, кото- рое принадлежит общему дереву с оптимальной полосой пропускания OBST (Optimal Bandwidth Shared Tree) или наборам ODST, рассчитывается коэффициент d с

Rank(T) = d x — + b x — p D p C

^T eODSTvOBST.

В данной формуле параметр D определен как максимально допустимая задержка передачи трафика VPN, зависящая от класса обслуживания. Параметр d_T определен как максимальная сквозная задержка между конечными точками VPN каждого дерева T , d _p и b _p – предпочтения по задержке и полосе пропускания соответственно. Параметр c_T определен как сумма полос пропускания по всем звеньям дерева T . Причем порог полосы пропускания C – максимальная полоса пропускания для деревьев в наборе ODST. Параметры по задержке и по полосе пропускания задаются с учетом требований пользователей. В итоге из найденных наборов выбирается лучшее решение относительно времени задержки и относительно требований по полосе пропускания, учитывающее заданные параметры пользователя. Авторы планировали в дальнейшем расширить схему ранжирования с учетом предпочтений пользователей, однако не представили классификацию трафика, передаваемого в сети VPN.

Выводы

Проведенный анализ имеющихся алгоритмов реализации моделей VPN с совместными ограничениями по задержке и полосе пропускания позволяет сформулировать их общие моменты и ключевые недостатки. Практически для всех алгоритмов характерны следующие условия решения поставленной задачи:

• -    используется потоковая модель VPN;

• -    трафик конечных точек VPN считается симметричным;

• -    топология VPN выбирается древовидной;

• -    трафик считается однородным (без выделения классов).

Основной практической проблемой решения задачи поиска пути, удовлетворяющего заданным ограничениям на задержку и полосу пропускания при передаче трафика VPN от отправителя до получателя, является ее высокая вычислительная сложность, вследствие чего решается она, как правило, приближенными и эвристическими методами. При решении задачи исследователи пытались получить алгоритмы, которые, с одной стороны, требуют резервирования минимальной полосы пропускания и/или обеспечивают минимальную задержку передаваемого трафика VPN, а с другой стороны – имеют небольшое время выполнения (высокую скорость).

Обобщив недостатки рассмотренных подходов, можно сделать следующие выводы.

• 1.    Некоторые методы и алгоритмы являются хорошо проработанными в теоретическом плане [4; 7] (определена верхняя граница порога для задержки), но слабыми в практическом отношении (отсутствуют результаты экспериментов на конкретных графах сетей).

• 2.    Предложенные эвристические методы [5-6] требуют небольших вычислительных затрат, но область практического применения их ограничена.

• 3.    Основным недостатком практически всех рассмотренных работ является однородность передаваемого трафика VPN. И хотя в [8-9] вводится классификация трафика, однако не рассматривалось решение задачи поиска оптимальной топологии VPN при передаче разнородного трафика.

Таким образом, актуальной теоретической задачей остается разработка методов и алгоритмов определения топологии VPN, удовлетворяющей одновременно ограничениям по задержке и полосе пропускания с учетом разнородного трафика виртуальной сети.