Анализ асимптотических свойств многомерной непараметрической регрессии

Непараметрическая регрессия, основанная на оценках плотности вероятности типа Розенблатта– Парзена [1; 2], использовалась при восстановлении однозначных стохастических зависимостей по статистическим данным наблюдений их переменных [3]. Для этой регрессии был разработан ряд модификаций в условиях малого [4], большого [5] объема статистических данных и при обработке неоднородной информации [6]. Непараметрическая регрессия является основным элементом структуры гибридных моделей, решающих правил оценивания состояния статических систем и временных процессов [7]. Уже установлены условия асимптотической сходимости непараметрической регрессии и ее модификаций, однако полученные результаты не позволяют определить количественную зависимость показателей эффективности исследуемых статистик от их параметров и особенностей априорной информации. Эта проблема усугубляется тем, что непараметрическая регрессия является оценкой условного математического ожидания. Нелинейный характер ее зависимости от непараметрических оценок плотностей вероятности случайных величин создает трудности при количественном анализе ее асимптотических свойств.

Исследование аппроксимационных свойств непараметрической регрессии значительно упрощается, если априорная информация содержит сведения о виде плотности вероятности аргументов восстанавливаемой зависимости. Такие сведения могут быть получены в результате предварительной обработки исходных статистических данных либо при их формировании в процессе активного эксперимента с исследуемым объектом. Цель данной статьи состоит в анализе асимптотических свойств многомерной непараметрической регрессии в зависимости от вида ядерной функции при известной плотности вероятности аргументов восстанавливаемой зависимости.

Непараметрическая регрессия и ее асимптотические свойства. Пусть V = ( x i , y i , i = 1, n ) - выборка, составленная из n независимых наблюдений случайной величины ( x = ( x . , v = 1, к ) , y ) с плотностью вероятности p ( x , y ) . Обозначим плотность вероят-

ности случайной величины x через p ( x ), а кривую регрессии y по x – через φ( x ): w

Ф (x )= J y p

-да

Будем считать, что плотность вероятности p ( x ) известна. В качестве приближения по исходным статистическим данным кривой регрессии примем статистику

n k Г      Yi ^

Ф1 ( x ) =----— Щ-т-¹ I,   <»

n p ( x ) П c . i =‘ v =1 ^ v '

. =1

где ядерные функции Ф ( и . ) удовлетворяет условиям H:

Ф( и. )"Ф(- и.), 0 <ф( и. )<«, Jф(и.)du. = 1, Jи2 Ф(и.)du. = 1,

Jи™ Ф(и.) du. <«, 0 < m <«; . = 1, к , а их коэффициенты размытости c. = c. (n) ^ 0 с ростом n. Здесь и далее бесконечные пределы интегрирования опускаются.

При синтезе статистики ф₁ ( x ) используется непараметрическая оценка p ( x , y ) многомерной плотности вероятности p ( x , y ) типа Розенблатта-Парзена [1; 2].

Для получения аналитически значимых результатов при исследовании свойств непараметрической регрессии будем считать, что интервалы изменения значений компонент x . , . = 1, к , вектора x одинаковы. В этих условиях появляется возможность полагать одинаковы ми значения коэффициентов размытости c . = c , . = 1, к , ядерных функций. Тогда непараметрическая регрессия (1) запишется в виде

1 ⁿ k Г Y — Y i ^

Ф ( x ⁾⁼ -ТмЕП ^Ф -.--.      (2)

nc p ( x ) i =1 . =1 ^ ^c )

Асимптотические свойства ф ( x ) определяются следующим утверждением.

Теорема. Пусть ф ( x ) , p ( x , y ) , p ( x ) * 0 и первые две их производные по каждой компоненте x v , v = 1, k , ограничены и непрерывны; ядерные функции Ф ( u_v ) удовлетворяют условиям H ; последовательности c = c ( n ) коэффициентов размытости ядерных функций такие, что при n ^ ж значения c ^ 0, а nc^k ^ж . Тогда непараметрическая оценка регрессии ф ( x ) обладает свойствами асимптотической несмещенности и состоятельности.

Д о к а з а т е л ь с т в о. По определению имеем

M (ф (X^ =   к 1 / х Х nc p(x) nk ■EJ— J у'Пф 1 =1              v=1

^Xv   ^X v A 1 '       ' \ J ' J ' J '

I

1            Jl. I x — t

= k , ч J—JyПФ|------Ip(y,ti,™,tk)dydti- dtk = c p (x )J       v=1 I c )

Jl, x — t

= _k , J — J ф ( t ) П ^Ф| -—-I p ( t i , - , t k ) ^dt i — ^dtk ,⁽³⁾ c p ( x )             v = 1 I ^c )

где M – знак математического ожидания. При выполнении данных преобразований учитывается, что элементы статистической выборки V являются значениями одних и тех же случайных величин ( t , y ) с плотностью вероятности p ( y , t ₁, — , t_k ) .

Проведем в выражении (3) замену переменных (xv — tv) c—1 = uv и разложим функции Ф(xv — ctv, v = 1, k), p(xv — ctv, v = 1, k) в ряд Тейло- ра в точке x. Тогда с учетом свойств H ядерных функций при достаточно больших значениях n получим асимптотическое выражение ческой регрессии смещения непараметри-

M ( ф ( x ) - ф ( x ) )

с ²

~

² p ( x )

Е ⁽ ф ^{( x} ) p ^{( x )) ( 2 )} + v =1

с ⁴

4 p ( x )

kk

Е Е ф V ²⁾ ( x ) p^X x ) v =1 r =1 r # v

k

Е ф V ) ( x ) p v ( x ) J u 4 ^ф ( u v ) du v I+ 0 ( c 6 ) , v =1                                          )

где фЕ( x ) , pX ( x ) , ( ф ( x ) p ( x ) )^{( 2 )} - вторые производные функций ф ( x ) , p ( x ) и их произведения по компоненте x_v ; символом 0 ( c ⁶ ) обозначены слагаемые степени малости порядка c 6 . Отсюда, из условия c ^ 0 при n ^ ж , следует свойство асимптотической несмещенности непараметрической регрессии ф ( x ) .

Для доказательства состоятельности оценки ф ( x ) вычислим ее дисперсию

D(ф(x)) = M(ф(x) — Ф(x))2 —(M(ф(x) — Ф(x)))2. (5)

Исследуем асимптотические свойства среднеквадратического отклонения:

M(ф (x) — ф(x))2 =

= M (ф2 (x)) — 2 ф(x)M (ф(x)) + ф2 (x).

Следуя ранее использованной технологии исследований, проведем преобразования:

M ( ф² ( x ) ) =

22 k 2 n c p ( x )

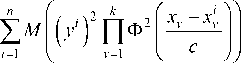
(            1 I _vy ^

+ ЕЕ м y ' П ф | ^Xv-^^v I y j Н' ф x x I i =1 j =1 У v =1 У ^c ) v =1 У ^c )_?

j *i

=TTkT^Z) [ n J—J Ф2(t1,—, tk)x nc p x хПФ21xv—v-1p(t1,—,tk)dt1— dtk +

v=1 У c )

+n (n—1)(J—J Ф (t1,—, tk)x xii ф[ x^—t11 p (t1,—,tk) dt1—dtk |

v=1 У c )                         )

Пренебрегая величинами малости

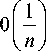
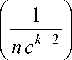
0 (c6), найдем значение асимптотическо- го выражения

M (Ф2(x)) ~ Ф2 (x)+ k1 Ф2 (x)x x 7 nc p(X)

x]i/Ф2 (u,) du, + -4л fit (Ф (X) p (X ))(2)T + v=1                   4 p ( X )У v=1

+ c 2 ф : е ( ф ( x ) p ( x ) ) ^{( 2 )} + c-^ x

1 (7)

kkk

Е ЕфV2^ (x) pr2^ (x) +Еф^ (x) pv2^ (x) J и4Ф( uv) duv v=1 r=1

r ^ v

.

Подставим выражения (4) и (7) в (6) и при достаточно больших n получим

M ( ф ( ^x ) ^— Ф ( ^x ) ) ² ~ ^Ф _k ^X ) ПJ ^{ф 2} ( ^u v ) ^du v ⁺ nc p ( X ) v =1

⁴ f                          ,-/ " ’

+          [Е(ф (X) p (X)) I .

^{4 p} ( ^X ) У v =1                  )

Отсюда, с учетом соотношений (4) и (8), из условия c ^ 0, nc^k ^ да при n ^ да следует свойство состоятельности непараметрической регрессии ф ( x ) .

При k = 1 результат (8) совпадает с утверждением работы [8], что подтверждает корректность выполненных преобразований.

Анализ аппроксимационных свойств статистики ф ( x ) . На основании полученных аналитических

Для исследования влияния вида ядерных функций на аппроксимационные свойства многомерной непараметрической регрессии определим отношение

R = W2 (ф(u ))

² W 2 ( Ф о ( u ) ) ,

результатов установим количественную зависимость аппроксимационных свойств ф ( x ) от вида ядерной функции и особенностей исходных статистических данных.

Определим минимальное значение W 2 выражения

где W ₂ ( Ф _о ( u ) ) , W ₂ ( ф ( u ) ) - значения критерия W ₂ (10) при ядерных функциях Ф _о ( u ) , Ф ( u ) . При этом по каждой компоненте u , , , = 1, k , использовались следующие ядерные функции:

ПI» 2 (Uv) du,

——nc k -----f — f ф² ( x ) p ¹ ( x ) dx 1 - ^dx k +

ф ( u , ) = ^ 76

I о

u v

v

I u , | < Тб

I u,\ > 76,

Ф ( u , ) = ( 2 n )^_ 1 ² e ^{_ u} 2/ ²,

с 4                                  ( 2)V

+tJ—fl p (x)i(ф(x)p(x))   I dxi -dxk, (9)

⁴ V          , =1                   J

которое получено путем интегрирования результата (8).

Из условия минимума (9) по коэффициенту размытости с нетрудно получить его оптимальное зна-

Iv u,|<75

ф (u,) = < 275

( о       v | u , |> 75,

Ф ( u , ) = 2 e ~^{72 7, 1}.

чение

* c

k            ^ k +4)

kA П1Ф2 (u,) du, ,=i nB

(11а)

(11б)

(11в)

(11г)

Нетрудно убедиться, что в данных условиях при

Ф ( u , ) = Ф ( u ) и Ф _о ( u , ) = Ф _о ( u ) , , = 1, k , отношение

R ₂ = a^{4 k ( k + 4 )} ,

где где

A = f — f ф² ( x ) p ¹ ( x ) dx 1 — dx_k ;

f Ф ² ( u ) du a = 4— 2-----.

I Ф 2 ( u ) du

(                         (2.7

B=f-fl p 1 (x)Ё(ф(x)p(x))   I dxi—dxk.

V , =1                    J

Тогда, подставляя c * в выражение (9), получим

( k . _	)	4 1	1/( k + 4)
A П1 Ф 2 , =1	( u , ) du ,	Bk	4 + k
n			4 k k /( k +4)

Дополнительно уменьшить значение W 2 можно за счет минимизации выражения | ф ² ( u , ) du , по виду ядерной функции Ф ( u , ) с учетом выполнения условий H .

Подобная задача решена в работе [2], в которой получена оптимальная форма ядерной функции

• ³ _ ^{3 u} 2

Фо (u, ) = ^ 475 2075 I о v |u,| < 75, v |u,| >55

Значения α приведены в работе [2].

Результаты вычислительных экспериментов при исследовании зависимости отношения R 2 от количества k аргументов восстанавливаемой зависимости и вида ядерных функций представлены в таблице.

Зависимость отношения R ₂ от количества k аргументов восстанавливаемой зависимости и вида ядерных функций

Ф ( u )	k = 1	k = 3	k = 5	k = 7	k = 9
(11а)	1,012	1,026	1,034	1,039	1,042
(11б)	1,041	1,089	1,117	1,135	1,148
(11в)	1,061	1,136	1,179	1,208	1,228
(11г)	1,249	1,61	1,853	2,027	2,157

С ростом размерности k вектора аргументов восстанавливаемой зависимости возрастает влияние выбора вида ядерной функции на аппроксимационные свойства многомерной непараметрической регрессии, что проявляется в увеличении значений отношения R2. Такая тенденция особо характерна для ядерных функций Ф(u) и Ф0(u), которым свойственны большие значения α. Например, отношение R2 для ядерной функции (11а) при k = 9 равно 1,042, а для (11г) – 2,157. При этом соответствующие им значения α равны 1,015 (11а) и 1,32 (11г).

На основе анализа асимптотических свойств многомерной непараметрической регрессии определена количественная зависимость ее аппроксимационных свойств от вида ядерной функции и особенностей статистических данных. В условиях их достаточно большого объема вид ядерной функции оказывает значимое влияние на среднеквадратическое отклонение непараметрической регрессии от условного математического ожидания, которое возрастает с увеличением размерности аргументов восстанавливаемой зависимости. Данная закономерность особо проявляется с увеличением степени отличия ядерной функции от оптимального ядра Епанечникова.