Анализ ценообразования опционов при условии трудно прогнозируемых событий, которые сильно влияют на рынок

Считается что справедливую стоимость опциона на финансовый актив, который торгуется на фондовом рынке можно однозначно определить по поведению базового актива. Одним из способов определения справедливой цены является модель ценообразования европейского опциона Блэка-Шоулза.

Оценка стоимости опционов используется как при хеджировании портфелей, так и в случае спекуляций для нахождения недооцененных и переоцененных опционов. Также модель Блэка-Шоулза позволяет оценить рыночные предпосылки по будущему значению волатильности.

Данная модель имеет некоторые допущения:

• •    По базовому активу опциона на покупку выплаты до экспирации опциона не происходят

• •    Нет транзакционных издержек при покупке и продаже опциона и базового актива

• •    Безрисковая процентная ставка постоянна во время действия опциона

• •    При покупке ценной бумаги можно привлекать средства по краткосрочной безрисковой ставке

• •    Короткая продажа ценных бумаг не ограничена, продавец получает деньги сразу

• •    Торговля базовым активом ведется непрерывно, поведение ее цены подчиняется законам геометрического Броуновского движения

При скачкообразном непредвиденном изменении цены основной вклад в расхождение стоимости опциона по модели Блэка-Шоулза и его реальной цены вносит допущение, что цена базового актива изменяется непрерывно и ведет себя по законам геометрического Броуновского движения, а также допущение, что математическое ожидание изменения цены базового актива равно 0, что неверно при наличии явного тренда.

Целью исследования является определить насколько модель ценообразования опционов точно может определить цену опциона, который торгуется на реальном рынке. Известно, что с учетом улыбки и ухмылки волатильности, модель Блэка-Шоулза определяет цены опционов точно для базовых активов, изменение цен которых непрерывно, т.е. цены базового актива изменяется постоянно на небольшую величину, математическое ожидание изменения цены базового актива рано нулю или пропорционально его предполагаемой доходности. Однако, интересно узнать каково расхождение цены, рассчитанной по модели Блэка-Шоулза и реальной цены опциона для базового актива, который котируется скачкообразно, с явным трендом, превышающим его доходность и обладает быстро растущей волатильностью. Также важно проанализировать зависимость расхождения цен опциона от изменения волатильности базового актива. С точки зрения поставленной задачи наиболее интересным было бы изучить колебания курса рубль-доллар в четвертом квартале 2014 года. Дальнейший расчет позволит нам выяснить, можно ли использовать модель Блэка-Шоулза для ценных бумаг, чьё движение цен не удовлетворяет закону геометрического Броуновского движения, и оценить зависимость ошибки расчетной цены от роста волатильности базового актива.

Для анализа будут использоваться десятиминутные бары USD000000TOD за 2014 год. Предполагаемый опцион будет являться call опционом с датой выпуска 1 сентября 2014 года и датой исполнения 31 января 2014 года. Данный период выбран по той причине, что в нем наблюдаются большие скачкообразные движения цены базового актива, т.е. USD000000TOD. Для простоты будем считать опцион in money, страйк цена которого будет 36.965 рублей, при этом влияние улыбки волатильности будет минимизировано. График движения цен базового актива представлен на рисунке 1. Серыми вертикальными линиями ограничен период существования рассматриваемого опциона.

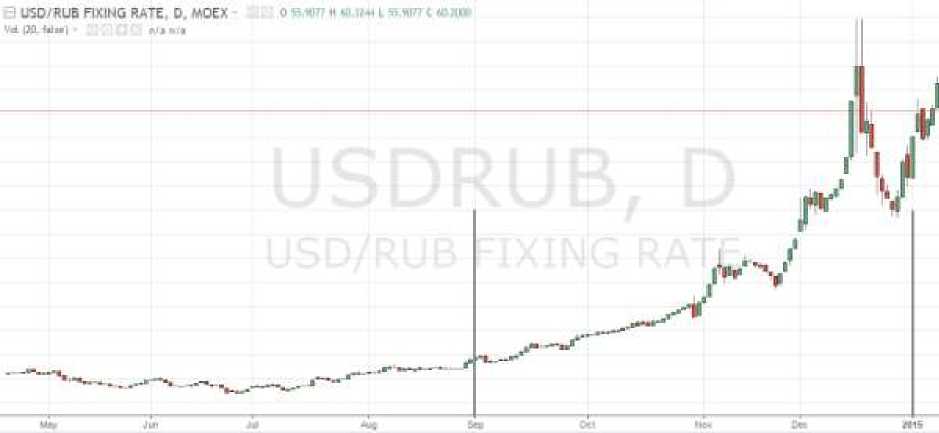
Рис. 1

Рассчитаем историческую и прогнозируемую волатильность базового актива за период с 2014.1.1 по 2014.9.1, т.е. за 2014 год до выпуска исследуемого опциона.

Для расчета прогнозируемой волатильности будем использовать экспоненциально взвешенную оценку среднего квадратического отклонения цены базового актива, т.к. она точнее работает на быстроизменяющихся данных, чем обычное среднеквадратическое отклонение.

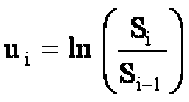
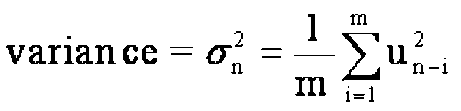
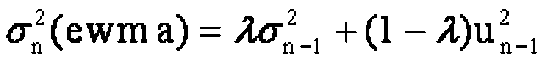
Рассчитанная таким образом волатильность имеет значение 27,7 % на 2014.09.01.

Для расчета исторической волатильности за указанный период воспользуемся формулой.

"^ n^Xi~^'

Историческая волатильность имеет значение 26,7%, что довольно близко к прогнозируемой и ожидаемо, т.к. цена базового актива осциллирует вокруг среднего значения.

Для определения справедливой цены опциона по модели Блэка-Шоулза будем использовать следующие формулы цена опциона v(LSt) = I ($:^‘ ~ К)рСуХу нк/у

К - цена исполенення. р(у) — плотность нормального распределения со средним а(Т -г) и дисперсией а~ (Т — г)

v(t S t) = S; Ф(х _ (t)) - К В тФ(х _ (t))Bt;

гдеВ, = е\

_ b(KS_t)  г _хд^

” а^/Т -t   о 2

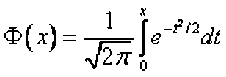
Имея справедливую цену опциона и цену базового актива можем рассчитать дельту, как отношение изменения цены опциона к изменению цены базового актива. Начальная цена опциона C0 = 2.838, конечная цена C1 = 3.234, начальная цена базового актива S0 = 36.965, конечная цена S1 = 37,377. Delta = (C1 – C0)/(S1 - S0) = 0.96.

Зная дельту опциона сможем вычислить реальную цену опциона. Создадим синтетическую позицию из длинной позиции опциона и короткой позиции дельта бумаг базового инструмента, т.е. 0,96 доллара. Таким образом у нас получится дельта нейтральная позиция, которую будем считать безрисковой с безрисковой доходностью 12% годовых. Из выше описанного, получим равенство, слева стоимость синтетической позиции в день выпуска опциона, справа стоимость синтетической позиции сразу после закрытия опциона.

С - 0. 96 * 37. 377 = е12^ * 0. 04 * 61, 877

Здесь С - реальная стоимость опциона, 0.96 - дельта, 37.377 -стоимость базового актива в день выпуска опциона, 0.12 - безрисковая ставка, 1/3 - интервал между выпуском и экспирацией опциона в годах, 0.04 = (1 - 0.96) , 61.877 - цена базового актива в момент экспирации опциона. С = 43,684 рубля.

Рассчитаем справедливые стоимости опциона по Блэка-Шоулза за весь период его существования. При этом для каждой новой цены будем пересчитывать экспоненциально взвешенную волатильность заново.

Также рассчитаем реальную стоимость опциона для каждого момента времени, за который есть котировка по базовому активу. Объединим графики стоимостей базового актива, реальной стоимости опциона и справедливой цены по Блэка-Шоулза.

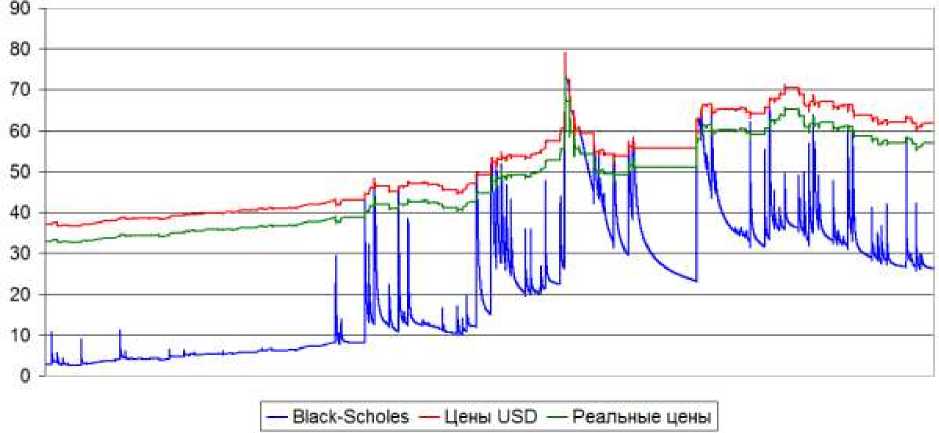
На графике видно, что реальная стоимость опциона повторяет движение стоимости базового актива, цена опциона по Блэка-Шоулза скачет и изредка пробивает реальную цену опциона. Цена опциона, рассчитанная по модели Блэка-Шоулза сильно реагирует на волатильность базового актива, это вызвано в том числе и тем, что ведется расчет экспоненциально взвешенной волатильности. В целом можно судить, что опцион недооценен при расчете его стоимости по модели Блэка-Шоулза, при резких скачках цены базового актива расчетная стоимость резко возрастает и превышает реальную. Большой вклад в расхождение реальной и справедливой цены вносит дельта. Очевидно, что с появлением скачков в цене базового актива и явно направленного тренда, дельта изменилась, а соответственно и реальная цена актива должна рассчитываться с новыми коэффициентами.

Исходя из полученных результатов, можно сказать, что валютные рынки, особенно в период экономической нестабильности не могут быть описаны диффузионной моделью, отсюда и некорректность оценки справедливой цены по модели Блэка-Шоулза. Для данного ценового ряда больше подошли бы модели, описывающие Леви процессы. Резкие скачки цены базового актива приводят к тому, что модель Блэка-Шоулза не успевает за резкими изменениями волатильности. По большому счету в период появления "Черного лебедя" рынок ведет себя непредсказуемо и среднесрочные и долгосрочные прогнозы неточны в любом случае. В данной ситуации уверенная торговля возможна при наличии инсайдерской информации или на очень краткосрочном периоде, используя технический анализ котировок базового актива.