Анализ частот продольных и поперечных колебаний сетчатой цилиндрической оболочки с отверстиями

Введение. На протяжении тридцати лет композитные сетчатые цилиндрические оболочки, обладающие высокой удельной прочностью и жесткостью, находят применение в ракетной и космической технике. История развития сетчатых конструкций, особенности их проектирования и изготовления представлена в статьях В. В. Васильева [1–5].

В последнее время композитные сетчатые цилиндрические оболочки широко применяются в качестве корпусов космических аппаратов [3]. Сетчатая оболочка является несущей конструкцией, к которой присоединяются приборы и механизмы космического аппарата. Силовая сетчатая оболочка с фрагментами оборудования показана на рис. 1.

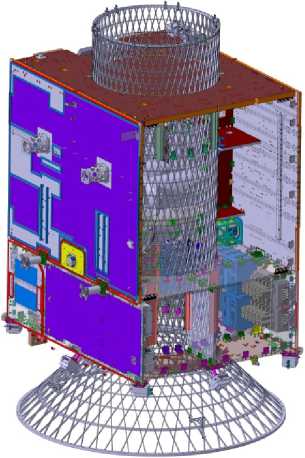
Рис. 1. Силовая сетчатая цилиндрическая оболочка космического аппарата

Один край такой оболочки прикреплен через адаптер к ракетоносителю. Сегодня используемые в качестве корпусов космических аппаратов сетчатые цилиндрические оболочки не имеют вырезов и отвер- стий в своей структуре. Это существенно затрудняет монтаж оборудования, стыковку кабельных разъёмов и трубопроводов, расположенных внутри сетчатого цилиндра. Очевидно, что наличие вырезов в сетчатой оболочке облегчит процесс монтажа оборудования, но вместе с тем повлияет на её жесткостные характеристики.

Отметим, что подавляющее число исследований композитных сетчатых цилиндрических оболочек [6–15] не рассматривают появления в них отверстий.

В настоящей статье решена задача определения первой частоты продольных и поперечных колебаний сетчатой цилиндрической оболочки, структура которой содержит отверстия (рис. 2). Один край оболочки жестко закреплен, а к другому краю прикреплен абсолютно жесткий диск. Выполнен анализ влияния размеров выреза и жесткости окаймляющего ребра на величину первой частоты колебаний.

Рис. 2. Сетчатая оболочка с отверстиями

Конечно-элементное моделирование. Модель сетчатой структуры оболочки как пространственной рамы была создана с помощью двухузлового элемента типа BEAM . Каждый из узлов конечного элемента обладает шестью степенями свободы. Это три перемещения и три угла поворота. Основой конечноэлементной модели сетчатой оболочки является типовой сегмент, показанный на рис. 3.

Типовой сегмент состоит из двух фрагментов спиральных ребер и фрагмента кольцевого ребра. Этапы построения конечно-элементной модели сетчатой цилиндрической оболочки представлены на рис. 4.

Первоначально создается конечно-элементная модель типового сегмента. На этом этапе определяются геометрические и упругие параметры ребер и размеры балочных конечных элементов. Затем с помощью процедуры зеркального отражения создается конечноэлементная модель двух связанных между собой типовых сегментов. На следующем этапе происходит копирование двойных типовых сегментов по окружности оболочки и создается пояс конечных элементов. Затем пояс двойных типовых сегментов, разбитых на конечные элементы, копируется вдоль оси оболочки. Завершает построение задание граничных условий и присоединение к сетчатой структуре элемента типа RIGID, с помощью которого моделируется абсолютно жесткий диск.

После построения конечно-элементной модели сетчатого цилиндра вырезается отверстие заданных размеров путем удаления соответствующих элементов сетчатой структуры. Жесткость окаймляющего ребра варьируется путем изменения размеров его поперечного сечения.

Численный анализ. Для проведения численного анализа была взята оболочка с диаметром D = 1,0 м, длиной L = 3 м и углом наклона спиральных ребер

φ = 25°. Масса жесткого диска, прикрепленного к свободному краю оболочки, равна m = 200 кг. Спиральные и кольцевые ребра рассматриваемой оболочки изготовлены из одного однонаправленного углепластика с модулем упругости E = 70 ГПа и плотностью ρ = 1550 кг/м³. Спиральные и кольцевые ребра имеют одинаковую ширину δ _s = δ _r = 0,002 м. Высота всех ребер h = 0,008 м (рис. 5).

Варьируемыми параметрами являются размеры отверстия a, b (рис. 6).

Ширина окаймляющего ребра может принимать следующие значения: δ ок = 0,002, 0,004, 0,006, 0,008, 0,012, 0,016, 0,024, 0,036 м.

В табл. 1 представлены значения первой собственной частоты продольных колебаний сетчатой оболочки с отверстиями рассматриваемых размеров. Графики изменения первой частоты продольных колебаний в зависимости от ширины окаймляющего ребра показаны на рис. 7.

Табл. 2 содержит значения первых частот поперечных колебаний сетчатой цилиндрической оболочки с отверстиями в плоскости XOZ . Зависимость частоты от ширины окаймляющего ребра представлена на рис. 8.

В табл. 3 представлены значения первой частоты поперечных колебаний сетчатой оболочки с отверстиями рассматриваемых размеров в плоскости YOZ . Графики изменения первой частоты поперечных колебаний в зависимости от ширины окаймляющего ребра показаны на рис. 9.

Характерная первая форма продольных колебаний сетчатой цилиндрической оболочки с отверстиями показана на рис. 10.

Первые формы поперечных колебаний сетчатой оболочки с отверстиями в плоскостях XOZ и YOZ представлены на рис. 11.

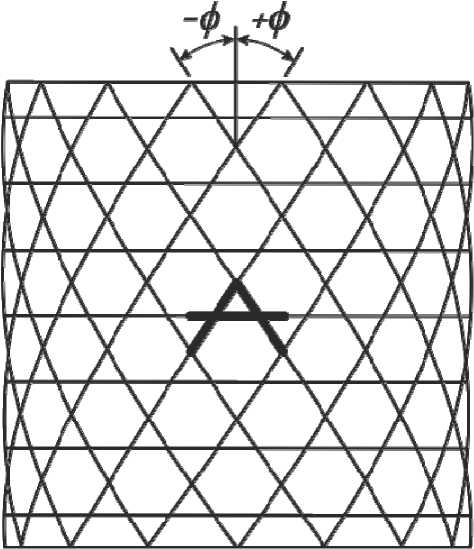
Рис. 3. Типовой сегмент сетчатой оболочки

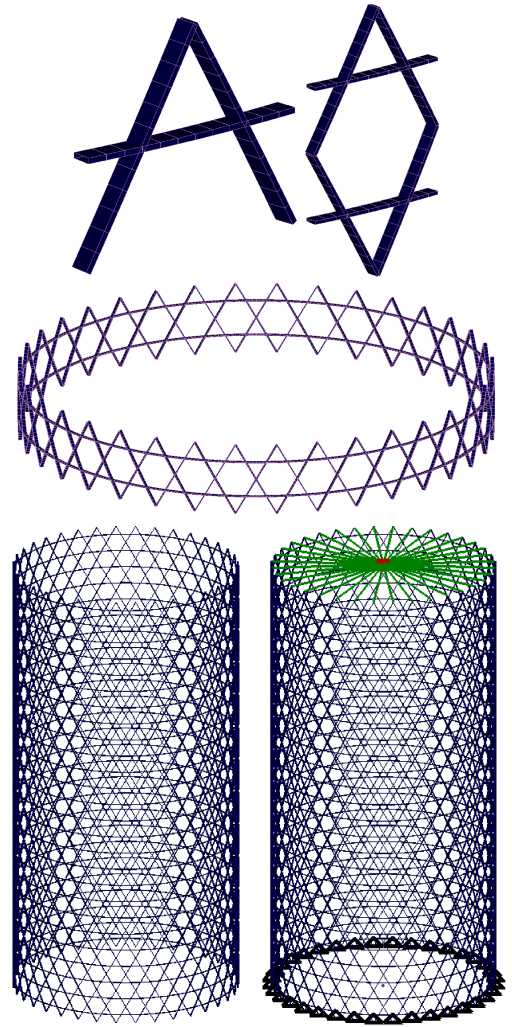
Рис. 4. Этапы построения конечно-элементной модели сетчатой цилиндрической оболочки

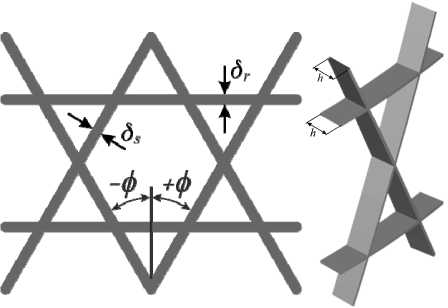
Рис. 5. Параметры сетчатой структуры

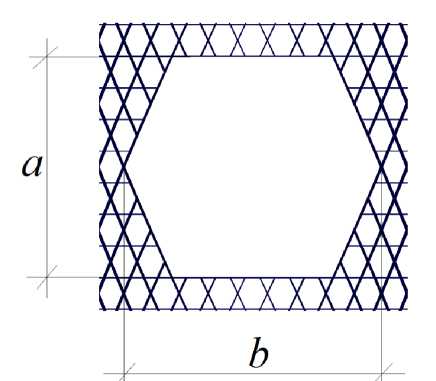
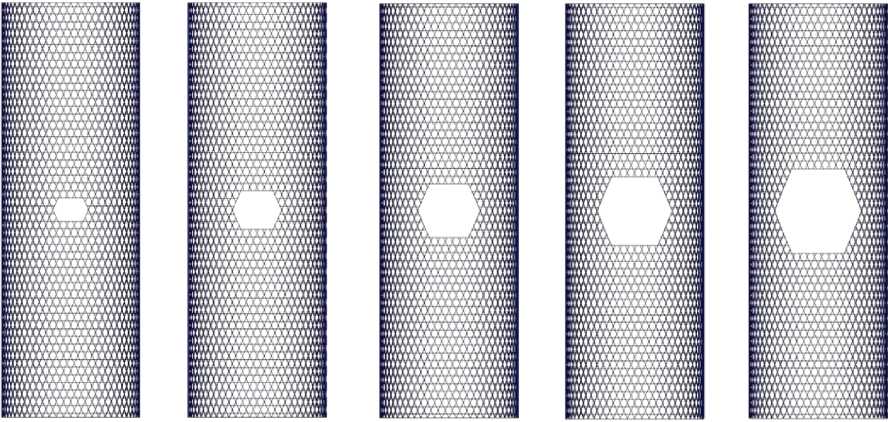
№ I №2 № 3 №4 №5 а=0,17л< а=0,28м а=0,39м а=0,5м а=0,61 Ь=0,2бл< Ь=0,36м Ъ=0,45м Ь=0,54м Ь=0 63

Рис. 6. Размеры отверстия в сетчатой структуре

Значения первой собственной частоты продольных колебаний сетчатой цилиндрической оболочки с отверстиями

Таблица 1

δ ок , м	Вариант структуры с отверстием
	№ 1	№ 2	№ 3	№ 4	№ 5
0,002	60,08	57,88	55,00	51,97	49,05
0,004	60,35	58,55	55,99	53,09	50,16
0,006	60,52	58,92	56,53	53,68	50,76
0,008	60,65	59,18	56,91	54,12	51,19
0,012	60,82	59,55	57,47	54,78	51,85
0,016	60,96	59,82	57,90	55,31	52,39
0,024	61,24	60,27	58,61	56,21	53,35
0,036	61,57	60,83	59,46	57,36	54,66

Таблица 2

δ ок , м	Вариант структуры с отверстием
	№ 1	№ 2	№ 3	№ 4	№ 5
0,002	10,62	10,16	9,29	8,12	6,91
0,004	10,67	10,29	9,53	8,44	7,24
0,006	10,70	10,36	9,68	8,66	7,48
0,008	10,71	10,41	9,78	8,82	7,66
0,012	10,74	10,48	9,93	9,04	7,93
0,016	10,76	10,53	10,03	9,20	8,13
0,024	10,80	10,63	10,21	9,47	8,45
0,036	10,84	10,73	10,43	9,82	8,90

Таблица 3

δ ок , м	Вариант структуры с отверстием
	№ 1	№ 2	№ 3	№ 4	№ 5
0,002	10,51	10,06	9,41	8,61	7,73
0,004	10,57	10,20	9,63	8,90	8,05
0,006	10,60	10,28	9,76	9,06	8,23
0,008	10,62	10,33	9,84	9,17	8,37
0,012	10,66	10,40	9,97	9,34	8,57
0,016	10,68	10,46	10,06	9,47	8,73
0,024	10,74	10,55	10,21	9,69	9,00
0,036	10,80	10,66	10,39	9,95	9,34

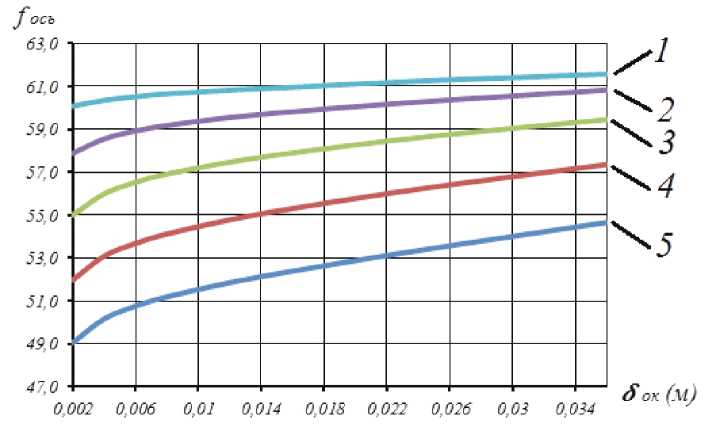
Рис. 7. Изменение первой собственной частоты продольных колебаний сетчатой цилиндрической оболочки в зависимости от ширины окаймляющего ребра δок

Значения первой частоты поперечных колебаний сетчатой цилиндрической оболочки с отверстиями в плоскости XOZ

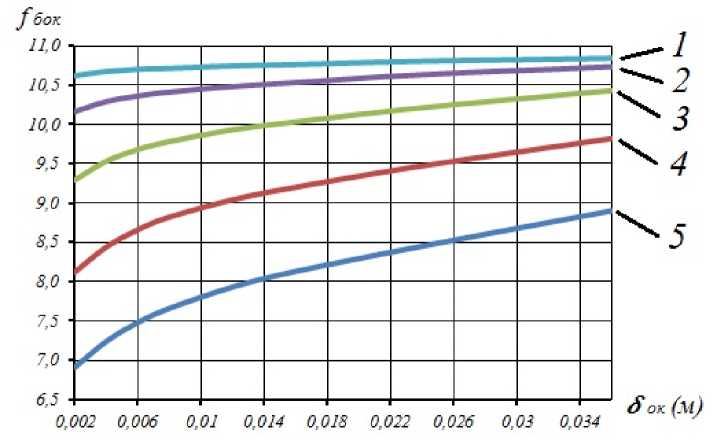
Рис. 8. Изменение первой частоты поперечных колебаний сетчатой цилиндрической оболочки с отверстиями в плоскости XOZ в зависимости от ширины окаймляющего ребра δ_ок

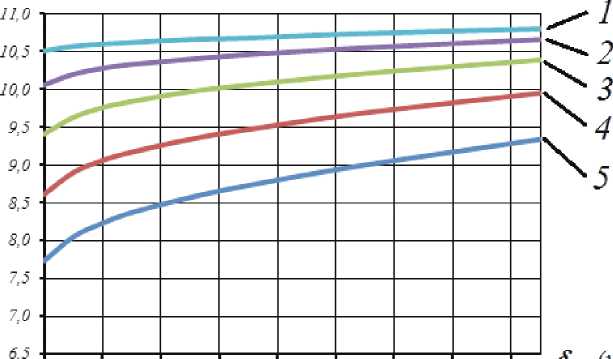
Значения первой частоты поперечных колебаний сетчатой цилиндрической оболочки с отверстиями в плоскости YOZ

fs™

0,002 0,006 0,01 0,014 0,018 0,022 0,026 0,03 0,034

Рис. 9. Изменение первой частоты поперечных колебаний сетчатой цилиндрической оболочки с отверстиями в плоскости YOZ в зависимости от ширины окаймляющего ребра δ_ок

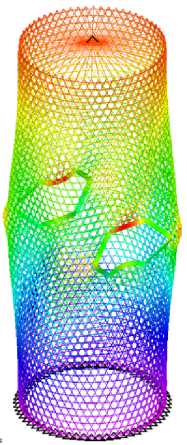
Рис. 10. Первая форма продольных колебаний сетчатой цилиндрической оболочки с отверстиями

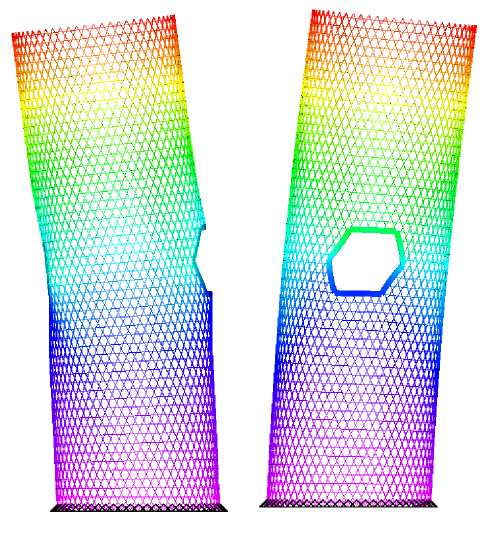
Рис. 11. Первые формы поперечных колебаний сетчатой оболочки с отверстиями в плоскостях XOZ и YOZ

Заключение. Первая частота продольных или поперечных колебаний оболочки является мерой соответствующей жесткости конструкции. Поэтому результаты выполненного модального анализа позволяют сделать определенные выводы о влиянии параметров вырезов на жесткость сетчатой оболочки. Очевидно, что вырезы уменьшают первую частоту продольных и поперечных колебаний оболочки. Окаймляющее ребро позволяет повысить жесткость оболочки с вырезами. По мере увеличения ширины этого ребра происходит увеличение соответствующих первых частот колебаний. Влияние ширины окаймляющего ребра тем заметнее, чем большими размерами обладает вырез в сетчатой структуре. Полученные результаты могут применяться при проектировании силовых конструкций космических аппаратов.

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation, unique identifier of the project RFMEF 157414X0082.