Анализ циклограммы поддержания низкой рабочей орбиты космического аппарата класса «АИСТ-2» с помощью электрореактивного двигателя

К настоящему времени накоплен опыт использования электрореактивных двигателей (ЭРД) на низкоорбитальных космических аппаратах (КА), функционирующих на высотах ниже 600 км. В период с 2009 по 2013 годы на сверхнизкой около-круговой орбите с высотой порядка 260 ÷ 280 км функционировал европейский КА «GOCE» с целью гравиметрических измерений Земли. Масса КА «GOCE» была порядка 1050 кг. Для удержания среднего радиуса орбиты использовался ЭРД с регулируемой тягой от 1 мН до 20 мН. Запас рабочего тела составлял 30 кг, что позволило поддерживать орбиту в течение 3,5 лет [1]. С 2012 года

запускаются российские малые КА дистанционного зондирования Земли (ДЗЗ) «Канопус-В», оснащенные отечественными ЭРД марки «СПД-50» (ОКБ «Факел», г. Калининград) для поддержания рабочей орбиты с высотой порядка 510 км [2]. В период с 2017 года по декабрь 2019 года осуществлялась миссия японского КА «Цубаме», как демонстратора технологий работы на сверхнизких орбитах. Масса КА составляла 380 кг. На КА «Цубаме» использовались химическая двигательная установка и электрореактивная двигательная установка. На последнем этапе миссии КА спустился на сверхнизкую орбиту высотой порядка 167 км и удерживался на этой орбите в течение недели. Ионный двигатель Кауфмана на КА «Цубаме» мог создавать регулируемую силу тяги от 10 мН до 28 мН, запас рабочего тела (ксенона) составлял 10 кг [3; 4].

К1ЛЕ АППАРАТЫ Ш

Том 4

Российский ракетно-космический центр «Прогресс» (г. Самара) с 2010-х развивает линейку малых КА ДЗЗ класса «АИСТ-2». В настоящее время на низкой околокруговой орбите функционирует малый КА ДЗЗ «АИСТ-2Д» с массой 530 кг. Спутник был запущен на начальную рабочую орбиту с параметрами: H _α = 493 км; H _π = 477 км, i = 97,2° [5]. На спутнике нет реактивных двигателей коррекции рабочей орбиты. Опыт эксплуатации этого КА показал, что за три года полета период обращения рабочей орбиты уменьшился на 10 секунд. Это изменение периода обращения эквивалентно уменьшению среднего радиуса орбиты на 15 км. Следует отметить, что КА «АИСТ-2Д» совершал свой полет в период крайне низкой солнечной активности, влияющей на уровень плотности верхней атмосферы Земли. В будущем, если уровень солнечной активности увеличится до средних и высоких значений, то возрастут плотность атмосферы и интенсивность падения высоты орбиты.

В настоящей статье рассмотрена задача анализа временных параметров циклограммы поддержания низкой орбиты малого КА класса «АИСТ-2» с помощью ЭРД на длительном интервале времени.

1. Постановка задачи

Объектом исследования является малый КА класса «АИСТ-2». В настоящем проектном анализе используются параметры массы и геометрии исследуемого КА. Проектный параметр масса КА ( m _КА ) имеет следующее пространство численных значений: 500 кг ≤ m _КА ≤ 700 кг.

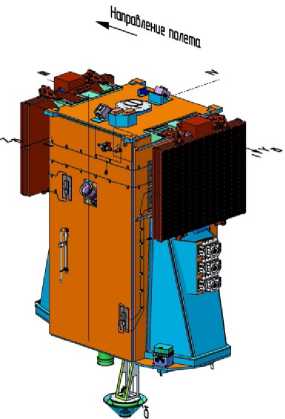
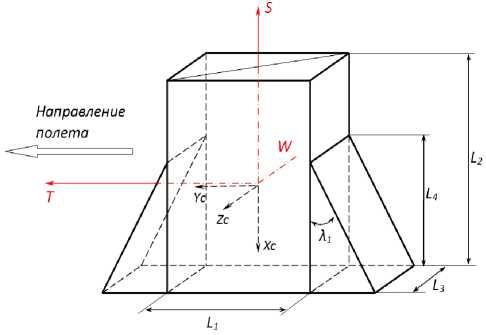
Геометрическая форма КА изменяется в зависимости от устанавливаемой на него целевой бортовой аппаратуры. На рис. 1 ( а , б ) показаны варианты различных КА на базе платформы «АИСТ-2». Геометрическая модель корпуса КА показана на рис. 1 ( в ).

Для расчетов параметров циклограммы поддержания низкой орбиты используется параметр эквивалентной площади миделя КА ( S _{экв.мид.} ), который зависит от линейных и угловых геометрических размеров корпуса КА, а также от площади солнечных батарей.

Математическую модель для определения эквивалентной площади миделя КА можно представить в виде выражения:

^S СБ ^S пов.КА

Sэкв.мид.= { sin 51С t) dS + J sin 52( t) dS, (1) 0 0

где SСБ – общая площадь солнечных батарей; Sпов.КА – общая площадь поверхности корпуса КА; δ1(t) – изменяющийся во времени угол между направлением аэродинамического потока и участка- ми поверхности солнечных батарей; δ2(t) – изменяющийся во времени угол между направлением аэродинамического потока и участками поверхности корпуса КА.

а

б

в

Рис. 1. Геометрия исследуемого объекта:

а ) КА «АИСТ-2Д» [5]; б ) проект КА со стереоскопической аппаратурой наблюдения; в ) геометрическая модель корпуса исследуемого КА

В настоящей статье описано исследование для ориентированного полета КА с неподвижными плоскостями панелей солнечных батарей, сориентированными параллельно аэродинамическому потоку разреженного газа, т. е. δ ₁ ( t ) = 0°. Соответственно, для разработанной геометрической модели КА в качестве исходных данных для исследований было сформировано следующее множество численных значений эквивалентной площади миделя: 1 м² ≤ S _{экв.мид.} ≤ 3 м².

Также в анализе был использован в качестве проектного параметра баллистический коэффициент КА (σ _КА ), который зависит от массы и эквивалентной площади миделя КА и определяется из выражения [6]:

° КА

= Сх •

экв.мид.

² m КА ^,

где C_х – коэффициент лобового сопротивления КА (при анализе C_x = 2,5). Для заданных множеств m _КА и S _{экв.мид.} из выражения (2) можно определить, что 0,003 м²/кг ≤ σ _КА ≤ 0,008 м²/кг.

Исследования проводились для низких око-лополярных (наклонение плоскости орбиты к экватору порядка 97°) и околокруговых орбит со средним радиусом орбиты ( R _орб.ср. ) от 6771 км до 6871 км. Для иллюстрации результатов анализа также использовался параметр средней высоты орбиты ( H _орб.ср. ): 400 км соответствуют 6771 км; 500 км соответствуют 6871 км.

Исследования проводились при состояниях атмосферы Земли, описываемых индексами уровня солнечной активности ( F ₀ ), изменяющих свое чис-

ленное значение в диапазоне:

75⋅10-22Вт/м2Гц ≤F ≤ 250⋅10-22Вт/м2Гц.

Анализ активных участков циклограммы поддержания орбиты (движение с включенным

ЭРД) проводился для силы тяги ЭРД ( F _ЭРД ), равной 20 мН. В расчетах было задано, что вектор силы тяги F _ЭРД направлен в положительном направлении по вектору орбитальной скорости КА.

Целью исследований являлось определение пространства численных значений параметров циклограммы поддержания орбиты КА: времени одного цикла коррекции ( t _ц ); времени пассивного движения КА под действием аэродинамических возмущений в цикле коррекции ( t _пас ); времени активного движения КА под действием малой силы тяги ЭРД ( t _акт ); моторного времени работы ЭРД за срок существования КА ( t _мот ); допустимого отклонения среднего радиуса рабочей орбиты КА (Δ R орб ).

2. Модель циклограммы поддержания низкой рабочей орбиты КА с помощью ЭРД малой тяги

Для анализа временных параметров циклограмм поддержания рабочей орбиты низкоорбитального КА использовалась модель циклов коррекции. На низкой орбите под воздействием аэродинамических сил сопротивления наиболее существенно эволюционируют такие параметры как большая полуось орбиты ( А ) и эксцентриситет (для низкой околокруговой орбиты R _орб.ср. = А ). Функционально зависимым от указанных параметров является период обращения на рабочей орбите. В настоящих исследованиях под коррекцией низкой орбиты понимается поддержание периода обращения ( T ) и, соответственно, большой полуоси ( А = R _орб.ср. ) на длительном интервале времени [7]. Циклограмму поддержания орбиты с помощью ЭРД при этом можно представить как на рис. 2.

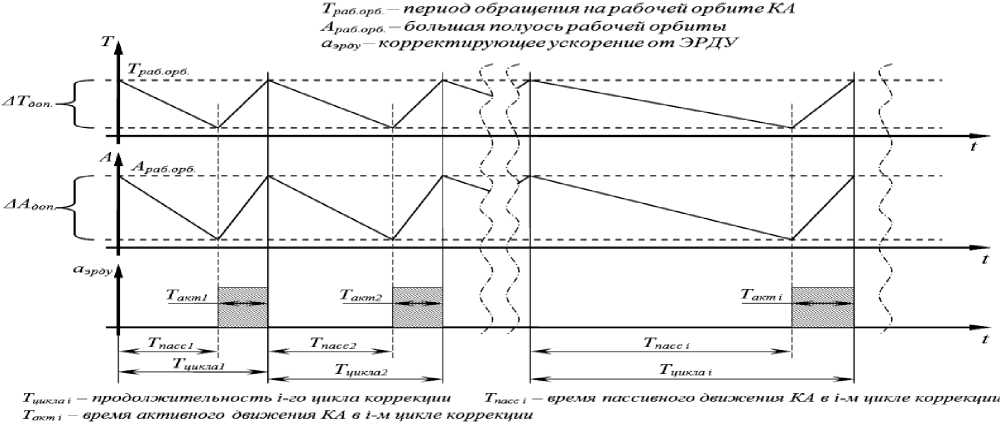
Рис. 2. Структура циклов поддержания орбиты КА с помощью ЭРД

(оСМИЧЕскиЕ

АППАРАТЫ И

Из рис. 2 видно, что циклограмма состоит из отдельных циклов коррекции, которые включают в себя участки пассивного и активного движения КА. На пассивных участках ЭРД не включается, а КА выполняет поставленные целевые задачи. Пассивный участок длится до тех пор, пока отклонение большой полуоси ( A = R _орб.ср. ) не достигнет допустимого значения Δ А _доп (Δ R _орб ). За пассивным участком следует активный участок, на котором ЭРД включается и создает корректирующее ускорение ( а _ЭРД ). Активный участок продолжается пока не восстановятся параметры орбиты.

За планируемый срок активного существования КА совершит определенное количество циклов коррекции, а суммарное моторное время работы ЭРД будет определяться из выражения:

n

TEMOm       Y i  Такт i, i=1

где T _{акт i} – время активного движения КА в i -м цикле коррекции орбиты; γ _i – относительное время работы ЭРД на активных витках в i -м цикле коррекции орбиты (в настоящих исследованиях γ _i = 1); n – количество циклов коррекции в течение срока активного существования КА.

• 3.    Методическое обеспечение для оценки уровня силы аэродинамического сопротивления

Для оценки величин силы аэродинамического сопротивления используется выражение [8; 9]:

F аэр

x экв.мид. ρ      ,

где ρ – плотность остаточной атмосферы Земли; V – скорость набегающего на КА аэродинамического потока.

Плотность верхней атмосферы Земли является высоко динамичной величиной, которая зависит от многих факторов: высоты над поверхностью Земли, уровня солнечной активности, геомагнитной возмущенности Земли и др. В исследованиях использовалась модель динамической атмосферы из ГОСТ Р25645.166-2004 «Атмосфера Земли верхняя. Модель плотности для баллистического обеспечения полетов искусственных спутников Земли». Согласно источнику плотность атмосферы в диапазоне высот от 120 км до 1500 км определяется из выражения [10]:

P = Ph - Kо-(1 + K 1 + K2 + Kз + K4),     (5)

где ρ _Н – плотность ночной атмосферы; K ₀ – изменение плотности атмосферы, связанное с отклонением средневзвешенного индекса солнечной ак-

Том 4

тивности F ₈₁ от фиксированного среднесуточного индекса солнечной активности F ₀ ; K ₁ – коэффициент суточного эффекта в распределении плотности; K ₂ – коэффициент полугодового эффекта; K ₃ – коэффициент, учитывающий изменение плотности, связанное с отклонением среднесуточного индекса солнечной активности F _10.7 от F ₈₁ ; K ₄ – коэффициент, учитывающий зависимость плотности атмосферы от геомагнитной активности.

Скорость набегающего аэродинамического потока равняется орбитальной скорости движения КА и определяется по моделям орбитального движения спутника Земли.

• 4.    Методическое обеспечение для анализа циклограммы поддержания низкой орбиты КА с помощью ЭРД

Расчет временных параметров циклограммы поддержания низкой рабочей орбиты осуществлялся с помощью численного моделирования движения КА под действием силы аэродинамического сопротивления и силы тяги ЭРД.

Схема организации численных расчетов показана на рис. 3, из которого видно, что в основе моделирования движения КА лежит численное интегрирование системы дифференциальных уравнений в оскулирующих элементах. Исходными данными являются временные параметры интегрирования и модель возмущающих ускорений a _возм = { T , S , W }, где { T , S , W } – проекции возмущающего ускорения на оси орбитальной системы координат: трансверсальной, радиальной и боковой.

Модель возмущающих ускорений в проекциях на оси орбитальной системы координат можно представить в виде выражений:

^Т возм = ^Таэр ⁺ ^РД;

S возм = S аэр ⁺ S ЭРД;                ⁽⁶⁾

Wвозм =-Wаэр + WЭРД, где {Tаэр, Sаэр, Wаэр} – проекции аэродинамического ускорения на трансверсальную, радиальную и боковую оси орбитальной системы координат; {TЭРД, SЭРД, WЭРД} – проекции реактивного ускорения от ЭРД на трансверсальную, радиальную и боковую оси орбитальной системы координат.

Для проведения описанных численных расчетов с целью получения параметров циклограммы коррекции было использовано разработанное авторами специальное программное обеспечение.

На основе серии численных экспериментов был получен массив временных параметров циклограммы поддержания низкой рабочей орбиты исследуемого КА в диапазоне заданных баллистических параметров и уровней солнечной активности.

Рис. 3. Схема организации численного расчета эволюции орбиты КА

5.    Результаты анализа времени пассивного движения КА в цикле коррекции

Исследования показали, что изменение среднего радиуса орбиты (Rорб.ср.) под действием силы аэродинамического сопротивления и малой силы тяги ЭРД в пределах 10 км от времени полета носит около линейный характер. Поэтому были проведены численные расчеты времени умень- шения среднего радиуса рабочей орбиты на 1 км в заданном пространстве проектно-баллистических параметров КА и уровней солнечной активности. Временные интервалы изменения среднего радиуса орбиты более чем на 1 км вычислялись по линейной зависимости.

На рис. 4 и 5 приведены результаты анализа времени пассивного движения ( t _пас ) КА в цикле коррекции до уменьшения среднего радиуса орбиты на Δ R _орб = 1 км.

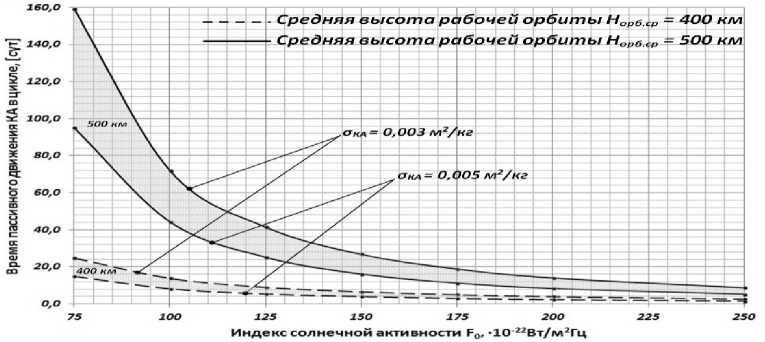
Рис. 4. Зависимость уменьшения радиуса орбиты КА на Δ R _орб = 1 км от уровня солнечной активности для 0,003 м²/кг ≤ σ_КА ≤ 0,005 м²/кг

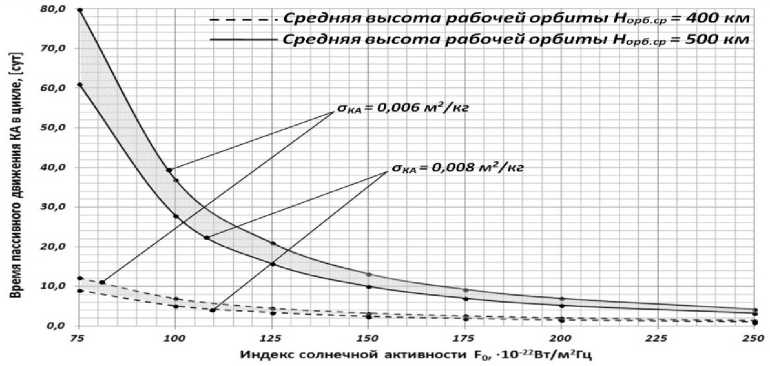
Рис. 5. Зависимость уменьшения радиуса орбиты КА на Δ R _орб = 1 км от уровня солнечной активности для 0,005 м²/кг ≤ σ_КА ≤ 0,008 м²/кг

КИЕ АППАРАТЫ И

Том 4

Обобщенные результаты по временным ин- на 1 км (пассивного движения КА), согласно об-тервалам уменьшения среднего радиуса орбиты ластям из рис. 4 и 5, приведены в табл. 1.

Таблица 1

Зависимость времени уменьшения среднего радиуса орбиты на Δ R _орб =1 км от баллистического коэффициента КА, сутки

Индекс уровня солнечной активности ( F 0)·10–22 Вт/м2Гц	Баллистический коэффициент КА, м2/кг
	0,003	0,005	0,006	0,008
Средняя высота начальной рабочей орбиты H орб.ср. = 400 км
75	24,7	14,9	12,2	9,1
100	13,8	8,2	6,9	5,1
125	9,0	5,4	4,5	3,4
150	6,6	4,0	3,2	2,4
175	5,0	3,0	2,5	1,9
200	4,0	2,3	2,0	1,5
250	2,7	1,6	1,3	1,0
Средняя высота начальной рабочей орбиты H орб.ср. = 500 км
75	159,0	94,9	80,0	61,1
100	71,8	44,2	37,0	27,9
125	41,4	25,1	21,0	15,7
150	26,7	16,0	13,2	10,0
175	18,8	11,2	9,3	7,0
200	14,0	8,3	7,0	5,2
250	8,7	5,2	4,3	3,2

6.    Результаты анализа времени активного движения КА в цикле коррекции

При движении на активном участке сила тяги коррекции орбиты с учетом аэродинамических потерь будет определяться из выражения:

Было определено, что в заданном пространстве проектно-баллистических параметров КА и уровней солнечной активности корректирующая сила тяги с учетом аэродинамических потерь может изменяться в диапазоне от 15 мН до 20 мН. На рис. 6 показана зависимость времени активного движения в цикле коррекции ( t _акт ) от накопленного отклонения среднего радиуса орбиты (Δ R _орб ) в следующем пространстве параметров КА и ЭРД:

F t = F эРд - F аэр.              (7)

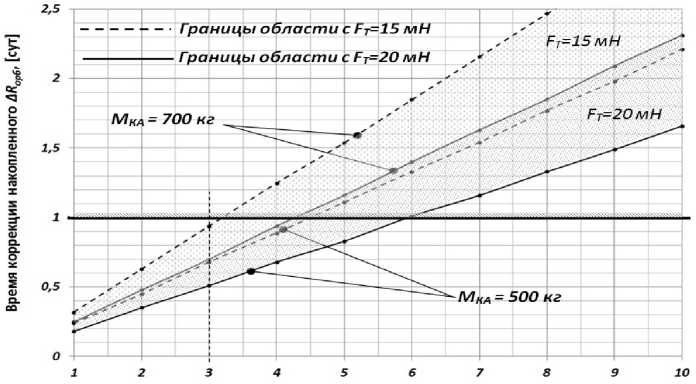
Отклонение рабочей орбиты AR_op6, [км]

Рис. 6. Время коррекции накопленного отклонения орбиты под действием силы тяги ЭРД с учетом аэродинамических потерь

500 кг ≤m ≤700 кг; 15 мН ≤F≤20 мН.

Из рис. 6 видно, что при отклонении радиуса орбиты Δ R _орб ≤ 3 км во всем пространстве проектно-баллистических параметров КА коррекцию можно осуществить менее чем за сутки (0,5 сут. ≤ t _акт ≤ 0,95 сут.). Если режим функционирования КА позволяет проводить коррекцию орбиты на интервале времени до 2-х суток, то отклонение среднего радиуса орбиты может достигать 6 ÷ 7 км.

7.    Синтез циклограммы поддержания низкой орбиты КА с помощью ЭРД

Был проведен синтез циклограммы поддержания низкой рабочей орбиты КА в диапазоне рабочих орбит со средней высотой от 400 км до 500 км, при условии допустимого отклонения

Δ R _орб = 3 км. Временные параметры циклов коррекции для граничных высот и уровней солнечной активности показаны на рис. 7 и 8.

В табл. 2 приведены обобщенные временные параметры одного цикла коррекции для баллистического коэффициента КА 0,003 м²/кг ≤ σ _КА ≤ 0,008 м²/кг при разных средних высотах орбиты и уровнях солнечной активности.

На основе полученных временных параметров циклов коррекции был проведен анализ моторного времени работы ЭРД с заданной силой тяги ( F _ЭРД =20 мН) в зависимости от срока существования КА. На рис. 9 и 10 показаны результаты оценки моторного времени ЭРД.

В табл. 3 приведены обобщенные результаты расчета моторного времени работы ЭРД для КА с баллистическим коэффициентом 0,003 м²/кг ≤ σ _КА ≤ 0,008 м²/кг при планируемом сроке существования от 1 года до 7 лет и крайних уровнях солнечной активности.

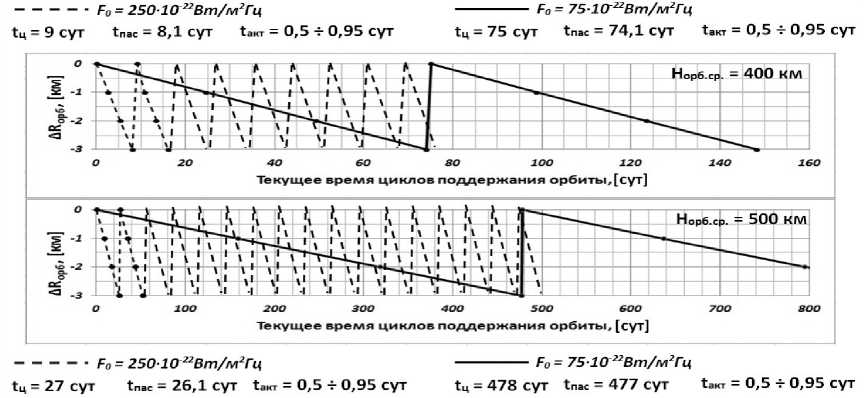
Рис. 7. Параметры циклов коррекции КА с σКА = 0,003 м2/кг для граничных значений высот рабочей орбиты и уровней солнечной активности

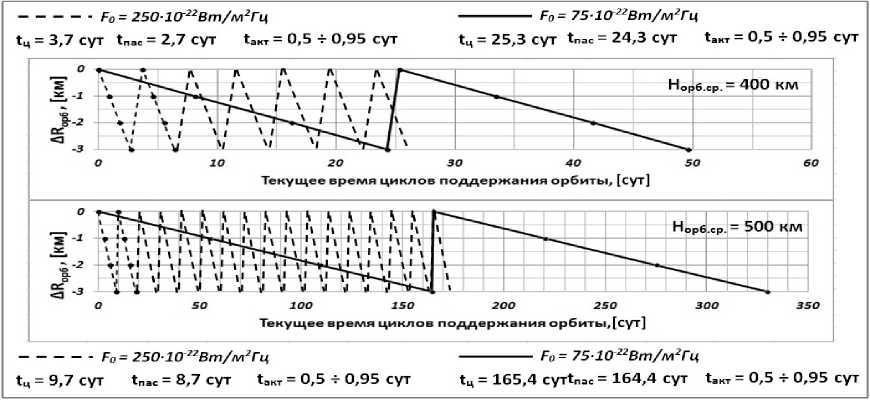
Рис. 8. Параметры циклов коррекции КА с σКА = 0,008 м2/кг для граничных значений высот рабочей орбиты и уровней солнечной активности

Том 4

Таблица 2

Временные параметры одного цикла коррекции, в зависимости от баллистического коэффициента КА (σ _КА ), при допустимом отклонении орбиты Δ R _орб = 3 км, сутки

Баллист. коэффициент КА (σ КА ), м2/кг	Индекс уровня солн. активности ( F 0 )·10–22 Вт/м2Гц	Временные параметры цикла коррекции орбиты: времени пассивного движения ( t пас); времени активного движения( t акт); общей продолжительности одного цикла ( t ц)
		при H орб.ср. = 400 км			при H орб.ср. = 500 км
		t пас , сут.	t акт , сут.	t ц , сут.	t пас , сут.	t акт , сут.	t ц , сут.
0,003	75	74,1	≤ 0,95	75,1	477	≤ 0,95	478
	250	8,1	≤ 0,95	9,1	26,1	≤ 0,95	27,1
0,005	75	44,7	≤ 0,95	45,7	284,7	≤ 0,95	285,7
	250	4,8	≤ 0,95	5,8	15,6	≤ 0,95	16,6
0,006	75	36,6	≤ 0,95	37,6	240	≤ 0,95	241
	250	3,9	≤ 0,95	4,9	12,9	≤ 0,95	13,9
0,008	75	24,3	≤ 0,95	25,3	164,4	≤ 0,95	165,4
	250	2,7	≤ 0,95	3,7	8,7	≤ 0,95	9,7

На основе полученных временных параметров циклов коррекции был проведен анализ моторного времени работы ЭРД с заданной силой

тяги ( F _ЭРД =20 мН) в зависимости от срока существования КА. На рис. 9 и 10 показаны результаты оценки моторного времени ЭРД.

0,0              1,0              2,0              3,0              4,0              5,0              6,0              7,0

Срок существования на рабочей орбите, [лет]

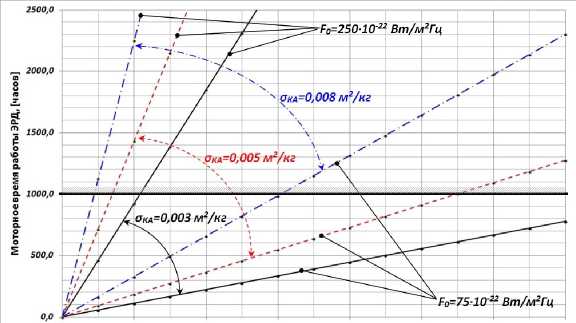
Рис. 9. Зависимость моторного времени работы ЭРД от срока существования КА на рабочей орбите со средней высотой около 400 км

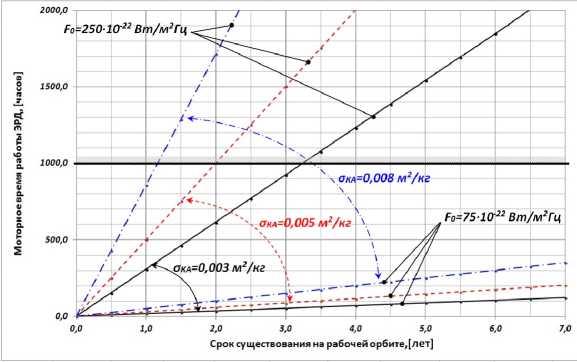
Рис. 10. Зависимость моторного времени работы ЭРД от срока существования КА на рабочей орбите со средней высотой около 500 км

Таблица 3

Срок существования, лет	F 0 = 75·10–22 Вт/м2Гц			F 0 = 250·10–22 Вт/м2Гц				69
	Баллистический коэффициент КА, м2/кг			Баллистический коэффициент КА, м2/кг
	0,003	0,005	0,008	0,003	0,005	0,008
при H орб.ср. = 400 км
1	111,0	182,1	328,9	924,7	1434,8	2249,2
2	221,9	364,2	657,9	1849,3	2869,7	4498,4
3	332,9	546,3	986,8	2774,0	4304,5	6747,6
4	443,8	728,4	1315,7	3698,7	5739,3	8996,8
5	554,8	910,5	1644,7	4623,3	7174,1	11245,9
6	665,8	1092,6	1973,6	5548,0	8609,0	13495,1
7	776,7	1274,7	2302,5	6472,7	10043,8	15744,3
при H орб.ср. = 500 км
1	17,4	29,1	50,3	308,2	501,3	857,9
2	34,8	58,3	100,6	616,4	1002,7	1715,9
3	52,2	87,4	150,9	924,7	1504,0	2573,8
4	69,6	116,5	201,3	1232,9	2005,3	3431,8
5	87,1	145,6	251,6	1541,1	2506,6	4289,7
6	104,5	174,8	301,9	1849,3	3008,0	5147,6
7	121,9	203,9	352,2	2157,6	3509,3	6005,6