Анализ динамических характеристик феррозондового датчика стыка свариваемых деталей

В системах автоматической ориентации электрода по стыку свариваемых деталей применяются измерительные устройства с феррозондовым датчиком стыка, измеряющим информационную составляющую магнитного поля переменного тока сварочного контура [1].

Традиционно феррозонды применяются для измерения магнитных полей в статическом режиме и достаточно полно освещены в научно-технической литературе [2–4]. Динамический характер функционирования автоматических систем, использующих феррозонд в контуре управления, предполагает обеспечение соответствующих требований к его динамическим свойствам, которые в большой степени определяются характером нагрузки измерительной обмотки. Сведения, касающиеся оценки феррозонда как элемента системы управления положением электрода в условиях дуговой сварки, когда информационное магнитное поле на 1,5...2 порядка меньше поля сварочного тока, отсутствуют. Это обстоятельство обусловливает целесообразность исследования динамических характеристик феррозонда и является предметом данной статьи.

Рассмотрим работу дифференциального феррозонда [2] с выходом на второй гармонике, нагруженного на комплексное сопротивление r , L , C (см. рисунок), при воздействии измеряемого поля H ( t ), слабого по сравнению с полем возбуждения.

Сигнал H(t) моделирует четные гармоники выходной ЭДС феррозонда, поэтому при выделении второй гармо- ники напряжение на нагрузке может быть представлено в виде

u(t) = U(t)∙cos2ωt, где U(t) = G2∙H(t) – огибающая выходного амплитудно-модулированного сигнала; G2 – коэффициент преобразования феррозонда по второй гармонике; ω – частота возбуждения.

Если входной сигнал H ( t ) имеет ограниченный спектр частот 0 ≤ Ω ≤ ω , то он может быть представлен преобразованием Фурье [5]:

ω

H ( t ) = ¹     H ( Ω ) e^{j Ω t}d Ω .

2π

- ω

В этом случае в огибающей несущего напряжения сохраняется полная информация о передаваемом сигнале при использовании амплитудной модуляции.

Амплитудные и фазовые частотные характеристики для огибающей выходного сигнала можно найти в предположении, что входной сигнал изменяется по следующему гармоническому закону:

H ( t ) = H ( Ω )∙cos Ω t .

Из этого соотношения видно, что огибающая выходного напряжения феррозонда изменяется по тому же закону. При этом амплитуда и фаза огибающей зависят от Ω . Таким образом,

u ( t ) = U ( Ω ) ∙ cos[ Ω t – ϕ ( Ω )]∙cos2 ω t ,

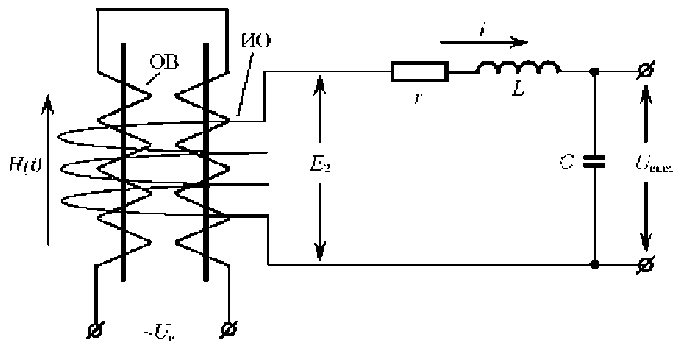
Феррозонд с нагрузкой: ИО – измерительная обмотка; ОВ – обмотка возбуждения;

Е ₂ – ЭДС измерительной обмотки; ~ U _в – напряжение возбуждения феррозонда частотой ω

где U ( Q ) = H ( Q ) G ₂( Q ) - амплитуда огибающей; ф ( Q ) -фаза огибающей выходного сигнала.

Задача сводится к определению функций G ₂( Q ) и <р( Q ), которые являются соответственно амплитудно-частотной и фазо-частотной характеристиками феррозонда для огибающей.

При гармоническом измеряемом поле ток в нагрузке феррозонда с выходом на второй гармонике содержит две составляющие с частотами (2 ю + Q ) и (2 ю - Q ) [5]:

⁺ 2 ^{j [}| I q , p | ^Sin( Ф q , p ^- Ф q 0 ) ] ^{+ + [}| I q , - p | ^sin( Ф q 0 ^- Ф q , - p ) ] .

Запишем последнее выражение в комплексной форме и определим частотную передаточную функцию феррозонда по огибающей:

I(t) = Ц^ COS [о + Q)t + ф q,p ] +

I (j j Q)

G  (jQ) = сфи 7

^сф        H ( j Q)

I q 0

I

+ q 2 p ^{cos [(2ю-Q)} t + ф q , - p J , где I q , p | и I q , - p | - модули; ^ф q , p и ^ф q , - p - фазы составляющих тока; q и p - номера гармонических составляющих частот щ и Q , соответственно.

Если модули и фазы составляющих суммарной и разностной частот равны, то изменение тока может быть представлено в виде амплитудно-модулированного колебания:

I ( t ) = 1 1 q p | COS Q t COS(2to t + ф q p ) .

Такое условие выполняется для низкой частоты измеряемого поля, т. е. при Q << ю.

Если частота измеряемого поля Q соизмерима с частотой возбуждения ю , такое приближение недопустимо. Упростить решение задачи в этом случае можно, если учесть, что характерной особенностью схемы выделения сигнала феррозонда является использование фазочувствительного демодулятора, который выделяет из входного сигнала только составляющую, синфазную с его опорным напряжением. Фаза опорного напряжения выбирается равной фазе ф q ₀, синфазной составляющей несущего колебания в статическом состоянии при постоянном измеряемом поле. При этом квадратурная составляющая модулированного колебания, фаза которой сдвинута на угол ± п /2 относительно опорного напряжения, не детектируется фазочувствительным демодулятором.

В общем случае, когда I q , p | * I q-p | и ^ф q , p * ^ф q-p , ток в нагрузке целесообразно представить в виде суммы синфазной I сф и квадратурной I _кв составляющих модулированного колебания

2 H ( j Q) 1 , 0

= I I q , p l

e ^(ф q , p ^{- ф} q 0 )

e ^-jv q ⁰ +

2 H ( j Q)

I

e (^ф 0 ^{- ф} q , - p )

¹ q 0

e^j^ q ⁰

,

где I q , _ p и I q , p - составляющие тока, сопряженные по гармоническим составляющим огибающей модулированного колебания.

Аналогично получим передаточную функцию для квадратурной составляющей (3):

G „ ( j fi) -

I ., ( j q) = I I . . , k ‘ "- - l I q , - , k * -• H ( j Q)        2 H ( j Q)

1(t) = 1:фCOS(2Юt + Ф q ,о) + 1квSin(2Юt + Ф q ,0), где

^ = ¹ | I q , - p |^COS(Q t — Ф q , - p ⁺ Ф q ,0 ) ⁺

2(2)

• ⁺ 2| I q , p |^COS(Q t ⁺ Ф q , p ^- Ф q ,0 ),

к в = ¹ | I q , - p | ^sin(Q t ^- Ф q , - p ⁺ Ф q ,0 ) ^-

• - 2 |Iq, p| COs(Q t - ф q, p - ф q ,0)-

• Синфазную составляющую полезного сигнала (2) представим в виде

I(jj ю) = с сф

= 2 [IIq,p I COS(Фq,p - Фq,0 ) + + |Iq,-p | COs(Ф q0 - Фq,p )] +

Рассматриваемая квадратурная составляющая, возникающая при воздействии на феррозонд переменного измеряемого поля, имеет место лишь тогда, когда составляющие боковых частот не равны, т. е.

|I q , p | * I q , - p |.

Этими же причинами обусловлено появление квадратурной составляющей при прохождении амплитудно-модулированного сигнала через частотно-избирательный фильтр с несимметричными амплитудно- и фазочастотной характеристиками.

Для переменного измеряемого поля с ограниченным спектром частот p Q <<  q ю , пользуясь приближенным соотношением [5; 6]

q ю ± p to    q to _ q ю    q ю ± p ю

2 pnfl - -p^)

= ±— L2 q ?2 „± 2 p^.

Г, pQ)      q ю q ю I 1 --I (   qю J представим напряжение на конденсаторе (см. рисунок) следующим образом:

_{=      =} wS Ц 2 H ( Q ) ( 1 ± j Q T + j y )

C = qp =   rC [(1 + jQt)2 - Y2 ] , где w - количество витков измерительной обмотки феррозонда; S - площадь сечения сердечников;

L1    ⁴..       1

р 2 = — = —p _max    h » -1 - вторая гармоника маг-

A   п      h ²

нитной проницаемости сердечников; L ₂ - вторая гармоника индуктивности измерительной обмотки; A = w ² Sl ^-1 -коэффициент пропорциональности; l - длина сердечника; h = HIH - относительная амплитуда поля возбуждения; H m - амплитуда поля возбуждения; H s - значение поля

насыщения сердечника; у = ю L 4 /г - коэффициент регене -рации; L ₄ – четвертая гармоника индуктивности измери-с                    2( L o ± L )     ' ^{2( L} 0 ^{+ L} ) "

тельной обмотки; т =--------, и т =-----------— - rr постоянные времени; L0 – индуктивность измерительной обмотки.

Учитывая, что [5; 6]

ej ф о = J± j Y_, 71 + Y²

определим следующее:

– коэффициент передачи феррозонда для огибающей синфазного напряжения (квадратурная составляющая не детектируется фазочувствительным демодулятором)

G = Uc (Q) = сф   H(Ω)

= —¹— ( U e ' ± U e 1 = 2 H (Q) ⁽ q ' p          q • " p     )

wS p₂ (1 ± у² ± j Qt')      ;

rC (1 - у² - Q² т² ± j Qt)V1 ± Y² ;

– относительную амплитудно-частотную характеристику феррозонда для огибающей

W ( Q ) = U c ^ =

U_{c 0}

Q2t'2

, ¹ ±       2 2

V (1 ± y²)²

Q ² t² )

1     2

Q ² t²  ’

⁺ (1 - Y²)²

– фазочастотную характеристику

Ф( ^Q ) = arctg  ---- ^- arctg  ----_{2       2}

1 ± y²        1 - Y 2 - Q² t²

В диапазоне частот, характеризуемом соотношением

Q²t² >> 1, при т ² « т выражение (4) можно упростить:

W ( Q ) «---

Qt 14

1 - Y²

Из выражения (5) видно, что феррозонд в динамичес- ком режиме эквивалентен инерционному звену первого порядка с передаточной функцией:

W ( j Q) э =

1 ± j Qт э

где т = т 1 ± Y2 = 2(L0 ± L)(1 ± Y)2 э 1 - y2        r (1 - y 2)

Q _э – эквивалентная добротность феррозонда.

Таким образом, приближенные расчеты коэффициента феррозонда для огибающей могут производиться по выражениям амплитудно-частотной и фазо-частотной характеристик эквивалентного инерционного звена:

71 ±Q² т 2

W ( j Q) =

ф(О) = - arctg От_э.

Для определения эквивалентного коэффициента передачи феррозонда достаточно найти постоянную времени т _э' которая может быть получена экспериментально или аналитически.

В резонансном режиме экспериментально может быть найдено значение эквивалентной добротности феррозонда Q _э, показывающее, во сколько раз возрастает его коэффициент преобразования для постоянного измеряемого поля, по сравнению с аналогичным коэффициентом в режиме холостого хода. Тогда, в соответствии с выражением (6), эквивалентная постоянная времени феррозонда оказывается в Q _э раз больше периода Т ₀ частоты возбуждения ю .

Расчетный способ определения ф_э при известных параметрах нагрузки r , L , C сводится к нахождению индуктивностей L ₀ и L ₄. Задавшись аппроксимирующей функцией кривой намагничивания сердечника феррозонда, для определения амплитуды поля возбуждения h можно найти значения L ₀ и L ₄ [2].

Таким образом, при оценке динамических характеристик феррозонда, цепь нагрузки которого настроена в резонанс на частоту второй гармоники, необходимо учитывать, что его статический коэффициент преобразования в Q _э раз выше, чем в режиме холостого хода, а постоянная времени возрастает в Q _э раз по сравнению с периодом частоты возбуждения.

При отсутствии резонанса в цепи нагрузки, т. е. при активной или активно-индуктивной нагрузке, а также в режиме холостого хода постоянная времени оказывается соизмеримой с периодом частоты возбуждения, и ее влиянием в большинстве случаев можно пренебречь, по сравнению со значительно большими постоянными времени фазочувствительного демодулятора и избирательного усилителя.

Точность расчета по приведенным формулам достаточна для анализа динамических характеристик феррозонда в резонансном режиме при эквивалентной добротности, достигающей значений от единиц до нескольких десятков.