Анализ динамических характеристик кластеров маховиков в системе управления ориентацией космического аппарата
Автор: Сомов С.Е., Сомова Т.Е.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6 т.23, 2021 года.
Бесплатный доступ
Представляются результаты сравнительного анализа динамических характеристик минимально избыточных кластеров двигателей-маховиков в отношении областей вариации векторов их кинетического и управляющего моментов, как в штатной конфигурации, так и при отказе любого одного двигателя-маховика в их составе.
Космический аппарат, управление ориентацией, кластеры маховиков, сравнение характеристик
Короткий адрес: https://sciup.org/148323599
IDR: 148323599 | УДК: 629.78 | DOI: 10.37313/1990-5378-2021-23-6-119-125
Текст научной статьи Анализ динамических характеристик кластеров маховиков в системе управления ориентацией космического аппарата
Для управления ориентацией любых космических аппаратов (КА) – спутников [1], космических роботов [2] и др. применяются реактивные двигатели-маховики и силовые гироскопы. Двигатели-маховики (ДМ) традиционно используются в системах управления ориентацией (СУО) как миниатюрных, так и крупногабаритных информационных спутников, когда КА не совершает быстрых поворотных манёвров и основное требование к электромеханическому приводу СУО заключается в обеспечении необходимой области вариации вектора его кинетического момента (КМ).
Здесь наиболее популярны минимально избыточные схемы на основе четырех ДМ: схема NASA, рис. 1 a , где оси вращения трех основных ДМ направлены вдоль осей канонической системы координат O x c g y c g z c g , фиксированной в связанной с корпусом КА системе координат (ССК) O xyz , а четвертый резервный ДМ – по пространственной биссектрисе между этими осями, и схема General Electric ( GE ), где оси вращения четырех ДМ расположены симметрично вдоль образующих линий кругового конуса с углом полу-раствора γ , рис.1 b .
Применение кластера ДМ по схеме NASA реализуется следующим образом: в начале миссии
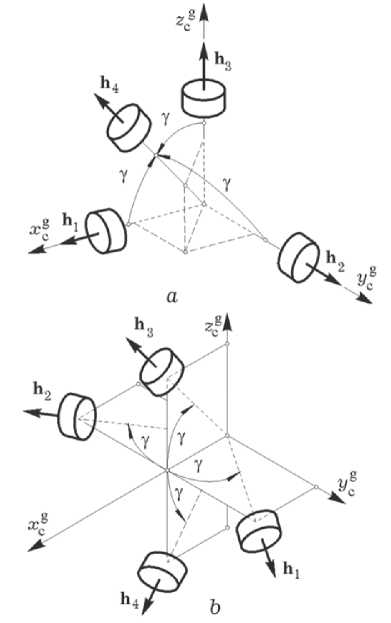
Рис. 1. Схемы кластеров NASA ( a ) и GE ( b )
КА работают три основных ДМ; при выходе из строя любого такого ДМ активируется четвертый резервный ДМ и кластер продолжает работать, но с уменьшенной областью вариации вектора его кинетического момента.
Кластер ДМ по схеме GE используется по-другому: в начале миссии КА работают все четыре ДМ; при отказе любого ДМ кластер остаётся работоспособным, но также с уменьшенной областью вариации вектора его КМ.
С целью обеспечения отказоустойчивости СУО проектирование кластера ДМ традиционно выполняется сразу для двух проектных конфигураций – стандартной (штатной) конфигурации, когда работоспособны все четыре ДМ, и резервной конфигурации, когда имеется отказ любого одного ДМ из трёх основных ДМ в схеме NASA и, соответственно, из четырёх ДМ в схеме GE .
Важная проблема возникает, когда любые два ДМ выходят из строя. В этом случае область вариации вектора КМ кластера ДМ представляется ромбом в соответствующей плоскости канонической системы координат, поэтому пространственное угловое движение КА не является полностью управляемым и целесообразно управлять ориентацией КА с помощью двух работоспособных ДМ и магнитного привода (МП) с цифровым управлением тремя электромагнитами. Отметим, что управление тандемом этих приводов является непростой задачей, так как вектор геомагнитной индукции существенно изменяется в ССК из-за пространственного движения КА и вращения Земли.
В статьях [3-5] мы исследовали задачу обеспечения живучести цифровой СУО мини-спутника землеобзора при всех шести вариантах возможных отказов двух ДМ в кластере по схеме GE . Установлено, что разработанные законы управления кластером ДМ и МП обеспечивают трассовую сканирующую съёмку земной поверхности, но не на любом участке орбиты путника и при снижении доступных ускорений КА в процессе его поворотных манёвров в двух вариантах отказов ДМ. В статье [6] выполнен сравнительный анализ основных энергетических характеристик кластеров маховиков и гироди-нов при управлении космическим роботом на геостационарной орбите.
В данной статье сравниваются динамические характеристики кластеров ДМ указанных типов в отношении размеров областей вариации векторов их кинетического и управляющего моментов, как в штатной конфигурации, так и при отказе любого одного ДМ в их составе.
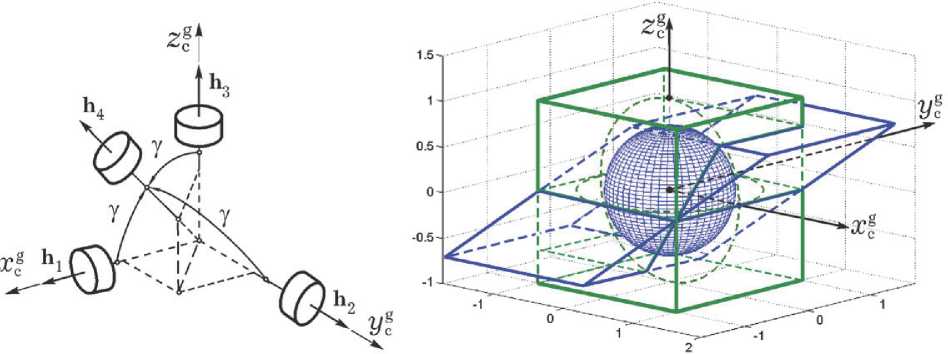
Рис. 2. Кластер ДМ по схеме NASA и области вариации вектора его КМ для двух конфигураций
МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ
Используются простейшая модель углового движения КА в виде свободного твердого тела с тензором инерции J , который совершает пространственное угловое движение с помощью кластера ДМ по схеме NASA либо GE , рис. 1. Наряду с ССК O xyz применяются инерциальная система координат, стандартные символы { • } = colQ, [ • ] = lineQ, ( - ) ‘ ,[ -х ] и ° ,~ для векторов, матриц и кватернионов, а также S а = sin а , C а = cos а и i = 1,2,.. m = 1 + m .
В инерциальной системе координат угловое движение КА определяется кватернионом Л , векторами угловой скорости го = { to i } и углового ускорения Ь = Е = { £ i }, i = 1 ^ 3. Вектор КМ любого из двух рассматриваемых кластеров ДМ представляется в ССК столбом Н = { H i }.
Будем считать, что при отсутствии внешних возмущающих моментов вектор G = J m ( t ) + Н ( t ) суммарного кинетического момента КА вместе с кластером ДМ удовлетворяет условию баланса G = 0 . В этом случае модель пространственного углового движения КА имеет простейший вид
Л = Л ° to /2; J b ( t ) = - Н ( t ) = М , (1) где столбец M = { M i } = - { H * } , i = 1 ^ 3, представляет вектор управляющего момента (УМ) соответствующего кластера и применяется символ ( • ) локальной производной вектора по времени.
Реактивный ДМ с номером # p е [1,2,3,4] вращается вокруг неподвижной в ССК оси с ортом ap, p = 1 ^ m, m = 4. При этом изменению вектора его КМ hp = hpap с ограниченным модулем | hp |= hp Пусть для простоты каноническая система координат O xgygzg (рис. 1) совпадает с ССК Oxyz, оси которой совмещены с главными центральными осями тензора инерции J = diag(J i) при максимальном Jm= max(Ji) и минимальном Jm= min(Ji) моментах инерции, соответственно. Для упрощения сравнения динамических характеристик кластеров также принимается, что одинаковый для всех ДМ осевой момент инерции Jr< Jmи не учитываются моменты всех сил сопротивления по осям вращения двигателей-маховиков. Задача заключается в расчете радиуса RH шара, вписанного в область вариации вектора H КМ сравниваемых кластеров ДМ как в штатной конфигурации, так и при отказе любого одного ДМ в их составе, а также в оценке радиуса RMшара, представляющего возможности соответствующего кластера ДМ по созданию вектора управляющего момента M в ССК. АНАЛИЗ ОБЛАСТЕЙ ВАРИАЦИИ ВЕКТОРОВ КМ И УМ КЛАСТЕРОВ Вводятся нормированные векторы КМ двигателей-маховиков hp = hpap с ограниченными модулями | h |= h = h /hm < 1, столбец нормированных КМ отдельных двигателей-маховиков h = {hp} и столбец нормированного КМ Н = {Hi} = {x, y, z} = Zhp кластера ДМ, которые связаны соотношением Н = Ah. Здесь матрица A = [ap ] соответствующей размерности представлена строкой, составленной из столбцов отображений ортов ap осей вращения ДМ на оси ССК Oxyz. Вводится также столбец m = {mp } нормированных УМ отдельных ДМ с компонентами mp = mp/mm. Радиус RHшара, вписанного в область вариации истинного кинетического момента кластера ДМ, связан очевидным соотношением RH= hmrHс радиусом rHаналогичного шара для нормированных векторов КМ двигателей-маховиков. Оси вращения ДМ фиксированы в ССК, поэтому при любой конфигурации кластера ДМ области вариации их векторов M и H являются конгруэнтными, а оценка радиуса RM шара, вписанного в область вариации вектора M получается по соотношению RM= mm rM, где rMпредставляет радиус аналогичного вписанного шара для нормированного вектора УМ M = {Mi} = M/mm. СХЕМА NASA Здесь орты ap осей вращения ДМ отображаются на оси ССК Oxyz столбцами а, = {1,0,0}; а2 = {0,1,0}; а3= {0,0,1}; а4= {a, a, a }, где a = CY = V1/3 = 0.57735, что соответствует значению угла у = 54°44'. Рис. 3. Область вариации вектора КМ кластера ДМ по схеме NASA при отказе ДМ #3 В штатной конфигурации такого кластера ДМ матрица А = [ap ], p = 1 + 3 имеет вид A = A3, где A3 = I3 при стандартном обозначении единичной матрицы 13. Область вариации вектора H нормированного КМ такого кластера ДМ представляется кубом, в который вписывается шар радиусом rH = 1, см. трёхмерное изображение в правой части рис. 2, зелёный цвет. При этом радиус rM шара, вписанного в об- СХЕМА GE В штатной конфигурации этого кластера ДМ (рис. 4) матрица A4 = [ap ], p = 1 ^ 4, расположения осей вращения ДМ в ССК формируется из столбцов ai = {Сy, 5y,0}; a2 = {Сy,-5y,0}; аз = {Сy ,0,5y }; a4= {Сy ,0,-5y}, ласть вариации нормированного вектора управляющего момента, имеет также очевидное значение rM = 1. При отказе любого из трех основных двигателей-маховиков включается резервный ДМ #4 с ортом a4= {a, a, a} оси его вращения в ССК. Для достижения максимальных значений нормированных радиусов rHи rMнеобходимо увеличение допустимых модулей векторов КМ и УМ резервного ДМ #4, именно следует принять h4 - h4 /hm < d4m и m4- m4 /mm < d4mс пара столбец h = {h p }, составленный из КМ hp, p = 1 ^ 4 отдельных ДМ, связан с вектором Н КМ кластера соотношением Н = А4h и вектор УМ кластера М =-Н =-А4m, где (3 х 4) - матрица A4 CY 5Y 0 С с Y Y ^^^^^^^в 5Y 5у CУ 0 " 5Y метром d4m = 1.216. При отказе, например, ДМ # 3, матрица A = A 3 = [a1, a 2, a 4] и обратная матрица A31 имеют вид "1 0 a 1 "10 -1" A 3 = 0 1 a ; A -1= 0 1 -1 ,(2) _0 0 a J [00 1/a Как известно [7], система векторов xp, p = 1 ^ m m p в евклидовом пространстве R является линейно независимой, если матрица Грама G, составленная их этих векторов, имеет определитель G = det (G) > 0, который равен квадрату объема m -мерного параллелепипеда, построенного на векторах x p, направленных по его ребрам. В рассматриваемом варианте класте- а область вариации вектора нормированного КМ такого кластера ДМ представлена в правой части рис. 2, синий цвет, а также на рис. 3. При таком варианте отказа в область вариации вектора H нормированного КМ кластера вписывается шар радиусом rH = 0.705, см. проекции и трёхмерное изображение на рис. 3. В итоге получаются значения радиусов RH = 0.705hmи RM= 0.705 mm. ра ДМ имеем m = 4, x p = ap и матрица Грама представляется в явном виде G = А4А4 = 16diag(C2 Sy2, S2) с определителем G = 16 CY Sy4. Выбор значения угла у в (4) основан на максимизации объема указанного параллеле- пипеда, что достигается при максимальном значении определителя G, когда d G / dу = 0. В результате получаются явные аналитические соотношения Рис. 4. Кластер ДМ по схеме GE в штатной конфигурации и область вариации вектора его КМ d G / dу = 16[-2 5YCy 5y4 + 4 C2 Cy 5 УПРАВЛЕНИЕ КЛАСТЕРОМ ДМ = 325yCy 5y2[-5y2 + 2 CJ] = 0; 5Y2= 2 CJ ^ tg y = V2 ; CY = a = 1/д/1 + tg2Y = 7173 = 0.57735; 5Y b = tg Y/V1 + tg2 Y = 7273 = 0.8165 0, по-прежнему при значении y = 54°44'. Область вариации нормированного КМ этого кластера ДМ с учетом двух плоскостей, где располагаются компланарные орты a1, a2и a3,a4соответственно, представляется в ССК десятигранником, каждая грань которого является ромбом, см. рис 4, зеленый цвет. В эту область вписывается шар радиусом rH = 25Y = 2^2/3 = 1.633, который касается всех 10 граней, см. рис. 4. В итоге получаются значения искомых радиусов При отсутствии избыточности кластера не возникает каких-либо проблем управления ДМ, см. матрицы A31(2) и (4). Для кластера по схеме GE в штатной конфигурации проблема заключается в распределении векторов КМ и УМ между избыточными числом ДМ. Здесь при матрице A4 (3) задача состоит в решении двух векторных уравнений А4h = Н V Н е R3, h е R4; А4m = -М = Н* V Ме R3, mе R4. () Распределение КМ и УМ двигателей-махови- RH = 1.633hmи RM= 1.633mm. HM В этой схеме при отказе, например, ДМ #4, матрица A = A3= [a,, a2, a3] и обратная ма- трица A3 1 имеют вид a a a qa qb-qb" A 3= b - b 0 ; A-1= qa -qb -qb , (4) 0 0 b J [ 0 - qb 1/b _ ков с их минимальным принуждением основано на применении псевдообратной матрицы 7 01 - 2 A # = A 4 G где qa = (2a)-1и qb = (2b) 1, и область вариации вектора нормированного КМ кластера представлена на рис. 5 вместе с вписанным в неё шаром радиусом rH = 0.816. В результате при данной конфигурации кластера ДМ получаются значения радиусов RH= 0.816hmи RM= 0.816mm. Но здесь отсутствует единственность решения уравнений (5), что приводит к накоплению погрешности [8]. Для устранения этого коварного эффекта были предложены различные подходы, например, представленные в патентах [9,10]. Мы применяем скалярную функцию настройки такого кластера для однозначного распределения векторов Н и M между ДМ по явным соотношениям [11]. Компоненты нормированного КМ кластера МД представляются как y = b(h1 -h2) ; z = b(h3 -h4), x = x1 + x2, где x1 = a(h1 + h2) и x2= a(h3+ h4). Распределение вектора H нормированного КМ осуществляется по закону Рис. 5. Область вариации вектора нормированного КМ кластера ДМ при отказе ДМ #4 f , (h) = x - X2+ p(xxX2-1) = 0, (6) где 0 <р<1, р = const; xi = xi / qy; ~2= x2/ qz, qs = (4 a2- s2)1/2, s = y,z, а также, при обозначениях c = x /2, d = qyqz - c2, соотношениями (i): q≡qy +qz; A =(qIp)(1-(1 -4p[(qy -qz)c + pd]/q2)1/2); x = (x + A)/2, x2= (x -A)/2 ; (ii) распределение КМ между ДМ в их парах по очевидным соотношениям; (iii) распределение вектора M по формуле m = {mp } = ({A 4, af})-1{-M, Фр (h)}, (7) где функция Фр(h) = -hmsat(фp, црf p (h)) имеет положительные параметры фр, Цри строка af= [a fp ] = df р (h) / dh имеет компоненты af2= 2^a[2a2 ±b2h2(h1-h2)][1 + pa^hilh4)]; ’ qy Qz f 2 a 2 2 a (hi + h 2) ai4= —r[2a + bh4(h3-h4)][1 + p---------]. ’ Qz Qy ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ В таб. 1 представлены значения радиуса rH шара, вписанного в область вариации нормированного вектора КМ сравниваемых кластеров ДМ, как при их штатной конфигурации (Штатн.), так и при отказе любого одного ДМ (Отказ ДМ). Учитывая подобие областей вариации векторов M и H, что отражается в одинаковых значениях радиусов rH и rMшаров, вписанных соответственно в области вариации нормированных векторов КМ и УМ этих кластеров, нетрудно убедиться в преимуществах схемы GE – «выигрыш» по rH и rMболее 63% в штатной конфигурации и 16 % при отказе любого одного ДМ, одинаковые ограничения на значения КМ и УМ для всех четырех ДМ. При штатной конфигурации сравниваемых кластеров ДМ потребные значения мощности и энергии кластера по схеме GE немного превышают аналогичные показатели кластера по схеме NASA. Этот эффект объясняется необходимостью дополнительных энергетических затрат [6] Таблица 1. Радиус rH шара вариации КМ ЗАКЛЮЧЕНИЕ Кратко представлены результаты сравнительного анализа динамических характеристик минимально избыточных кластеров двигателей-маховиков по схемам NASA и General Electric, как в штатной конфигурации, так и при отказе любого одного двигателя-маховика в их составе. Установлены преимущества схемы General Electric по размерам областей вариации векторов их кинетического и управляющего моментов, но в штатной конфигурации эта схема немного «проигрывает» схеме NASA в отношении потребных значений мощности и энергии из-за дополнительных энергетических затрат для настройки кластера четырёх ДМ при исключении его избыточности.
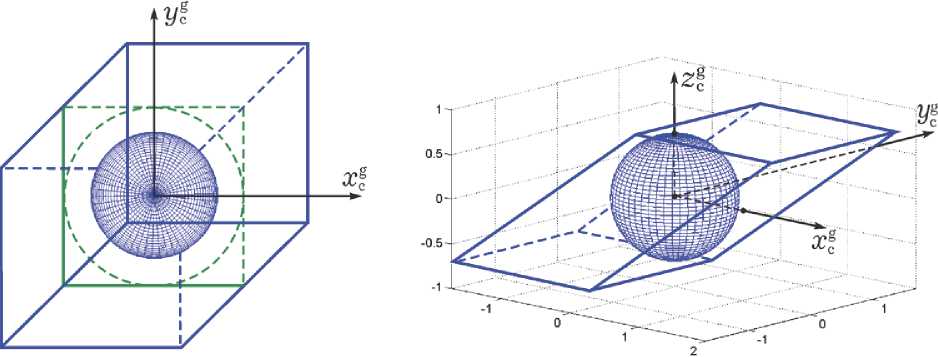
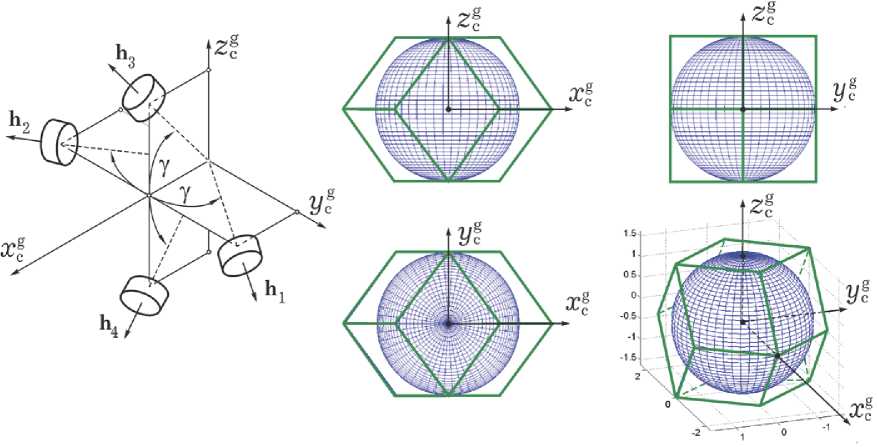
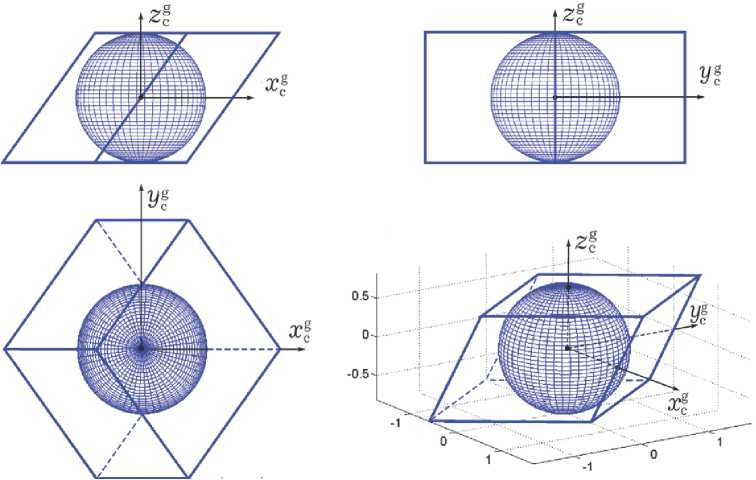
Схема NASA
Схема GE
Штата.
Отказ ДМ
Штата.
Отказ ДМ
1.00
0.705
1.633
0.816
для настройки кластера четырёх ДМ с целью исключения его избыточности.
Список литературы Анализ динамических характеристик кластеров маховиков в системе управления ориентацией космического аппарата
- Testoyedov N., Rayevsky V., Somov Ye., Titov G., Yakimov Ye. Attitude and orbit control systems of Russian communication, navigation and geodesic satellites: History, present and future. IFAC PapersOnLine. 2017. Vol. 50, no. 1, pp. 6422-6427.
- Somov Ye., Butyrin S., Somov S., Somova T. Control of robot-manipulator during its preparation and capture of a passive satellite. Mathematics in Engineering, Science and Aerospace. 2019. Vol. 10, no. 3, pp. 421-432.
- Сомов С.Е., Сомова Т.Е. Обеспечение живучести системы управления ориентацией спутника зем-леобзора при отказах роторных приводов // Известия Самарского научного центра РАН. 2018. Т. 20, № 6. С. 190-195.
- Somov S., Somova T. Ensuring survivability of spacecraft attitude control system at failures in flywheel cluster. Journal of Aeronautics and Space Technologies. 2021. Vol. 14, no. 1, pp. 89-98.
- Сомов С.Е., Сомова Т.Е. Обеспечение живучести системы управления космическим аппаратом при критических отказах реактивных маховиков // Известия Самарского научного центра РАН. 2021. Т. 23, № 2. С. 66-74.
- Сомов Е.И., Бутырин С.А., Сомова Т.Е. Анализ динамических свойств маховиков и гиродинов для управления космическим роботом на геостационарной орбите // Известия Самарского научного центра РАН. 2021. Т. 23, № 2. С. 84-90.
- Гантмахер Ф. Р. Теория матриц. М.: Наука, 1988, 552 с.
- Алберт А Регрессия, псевдоинверсия и рекуррентное оценивание. М.: Наука, 1977, 224 с.
- Reckdahl K.J. Wheel speed control system for spacecraft with rejection of null space wheel momentum. USA Patent no. 6141606, 2000.
- Ratan S., Li X. Optimal speed management for reaction wheel control system and method. USA Patent no. 7198232, 2007.
- Somova T. Attitude guidance and control, simulation and animation of a land-survey mini-satellite motion. Journal of Aeronautics and Space Technologies. 2016. Vol. 9, no. 2, pp. 35-45.


