Анализ динамических нагрузок на элементы конструкции гусеничных лесопогрузчиков при внешних воздействиях в виде стационарных случайных процессов

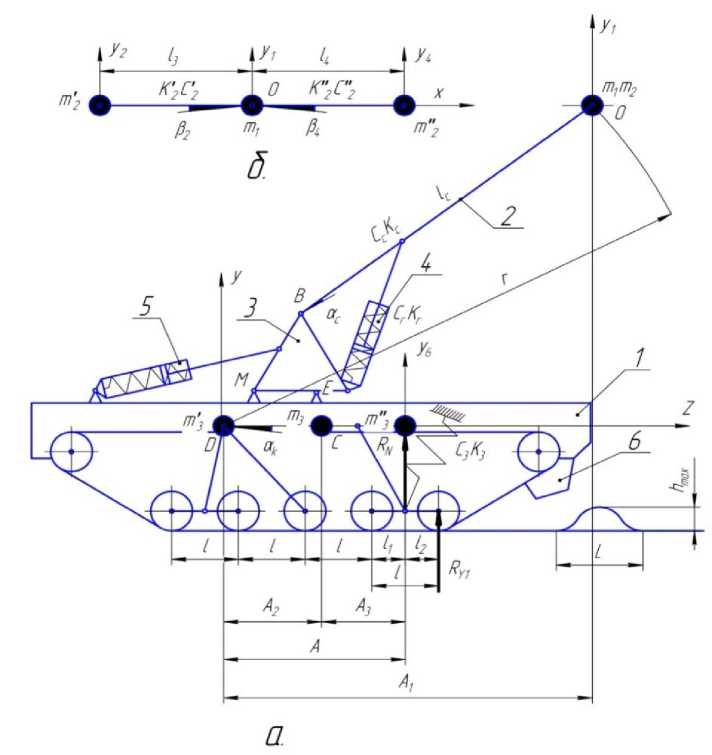
Рис. 1. Эквивалентная расчетная схема: а – с жестким грузом в захвате (сортиментами);

б – схема размещения упругого груза (хлыстов) в захвате; 1 – корпус, 2 – стрела,

3 – основание поворотное; 4,5 – гидроцилиндры привода, 6 – опора

На рисунке 1 представлена эквивалентная расчетная схема гусеничного лесопогрузчика на базе лесопромышленного трактора с полужесткой подвеской корпуса при движении с упругим грузом (хлыстами) и жестким грузом (сортиментами), разработанная с учетом особенностей конструкции машины и свойств предмета труда.

Обозначения на схеме:

m ₁ – масса подвижных частей рабочего оборудования, динамически приведенная к концу стрелы;

m ₂ – масса жесткого груза, приведенная к концу стрелы;

m ₂ ′ , m ₂ ′′ – массы вершинной и комлевой частей расчетных деревьев, приведенные в их центры тяжести;

m ₃ – подрессоренная масса базовой машины и неподвижных частей рабочего оборудования;

C ₂ ′ , C ₂ ′′ – изгибная жесткость вершинной и комлевой частей деревьев, приведенная в центры масс;

K ₂ ′ , K ₂ ′′ – демпфирующие сопротивления вершинной и комлевой частей деревьев;

• К С , К Г ,К 3 – составляющие демпфирующих сопротивлений – соответственно стрелы, гидросистемы, рессор подвески корпуса трактора.

В качестве обобщенных координат, определяющих положение масс m 1 , m 2 , m 3 , приняты линейные перемещения y 1 , y 6 , y 2 , y 4 .

Параметры m 3 , y 6 , c 3 , k 3 приведены к центру массы m 1 .

• А, А 1 ,А 2 ,А 3 ,А 5 – линейные размеры базовой машины и технологического оборудования; l 3 ,l 4 – размеры вершинной и комлевой частей деревьев; L, h max – размеры препятствий; q i (t) – внешние возмущающие воздействия (реакции опорной поверхности).

Математические модели лесопогрузчиков разработаны в виде систем неоднородных дифференциальных уравнений второго порядка. Система (1) описывает состояние лесопогрузчика при движении с жестким грузом (сортиментами), система (2) – при движении с упругим грузом (хлыстами).

ll y + пУyi - 2Пб ■ —c • y6 + ^6 y - A6 ■ — • Уб =

(             ^Q 1 ^{( t} t

( m i + m 2 ) l

. A ,  - A a}

У б +    ■ ^2ry У б ¹ \ л

A        \ A y

■ .2 ■ ^A 7 y 6 ^-   АУ y +

AA

+ llAA ■ А Уб - A ■ 2^6y + l A ■ 2^8 y6 = -1- Q(t) A     A    Am

Y + А2 Y - А2 Y + 2nY - 2nY = Q, (t)--- 2    2 2    21     22     212

m ₂ l ₃

Y + А Y 4 - А Yi + 2^ - 2^ = Q 4 ( t) — m 2 l 4

Y + Ai Y - Ai Y6 c-+2nY - 2пАб у— ®4 Y2+Al Yi - А> Y4 + А Yi -6A             6A 42   4     545

- 2y Y4 + 2п Yi - 2^ Y2 + 274 Y = Qi (t) — m lC

2      2 A 2  lC AA

Y 6 ⁺ 2 ^П 7 Y 6 ^{+ A} 7 Y 6 - ^A 8 Y i     ' ^A 8 Y 6   .2 - 2 ^П 8 Y i ~ ⁺

AAA

= Q 3 ( t )

m 3 A

lA

+ 2% Y6 C A где Ai - парциальные частоты [1];

n i - удельные демпфирующие сопротивления [1];

Q _i ( t ) – внешние возмущающие воздействия на систему.

В работах [2, 3, 4, 6] по исследованию нагрузок на линейные динамические системы машин последние рассматриваются в виде систем автоматического регулирования с обратной связью, на вход которых подаются возмущения в виде гармонических или случайных функций. Свойство линейных динамических систем сохранять закон проходящих сигналов позволяет получать энергетические спектры выходных параметров в виде тех же функций. Выходными параметрами являются перемещения, скорости, ускорения вынужденных колебаний, а также динамические нагрузки на элементы конструкции машин. При этом используется уравнение

S y ^{А )=} | w ^A ) ² ■ S x (А,

где I W(А) I - модуль амплитудно-фазовой частотной характеристики системы (амплитудно-частотная характеристика);

S y А) — энергетический спектр параметра выходного процесса - нагрузок на элементы конструкции машины;

S x А) - энергетический спектр параметра входного процесса - внешних возмущающих воздействий на систему;

а - круговая частота вынужденных колебаний системы.

Данное уравнение позволяет по известным характеристикам случайных процессов внешних воздействий и свойствам динамических систем получать соответствующие характеристики случайных процессов динамических воздействий на элементы конструкции (на выходе системы). При исследованиях и расчетах лесопогрузчиков в качестве характеристик внешних воздействий использованы спектральные плотности процессов силового взаимодействия ходовой системы и корпуса лесопогрузчика с опорным массивом – Sx(f), полученные путем статистической обработки результатов экспериментальных исследований данных процессов [1].

Модули амплитудно-фазовых частотных характеристик систем (амплитудно-частотные характеристики) определялись путем прямого преобразования Лапласа и Фурье систем дифференциальных уравнений (1), (2), которые предварительно представляются в операторной форме, т.е. с использованием операторов дифференцирования p = d/dt ; p ² = d ² /dt² . При преобразовании Лапласа дифференциальных уравнений с целью получения выражений передаточных функций динамических систем оператор дифференцирования Р заменяется комплексным числом S. Передаточной функцией динамической системы называется отношение преобразования Лапласа выходной координаты y 1 (s) к преобразованию Лапласа функции воздействия F 1 (s). Так как передаточная функция является комплексной, она определяет соотношение амплитуды выходного параметра к амплитуде входного и сдвиг по фазе между данными параметрами.

Для определения из выражений передаточных функций и амплитудно-фазовых частотных характеристик необходимо перейти от преобразования Лапласа к преобразованию Фурье представлением комплексного числа в виде S = ia - комплексной частоты (а - круговая частота, 1 2 = -1). Переходя от преобразований Лапласа к преобразованию Фурье, получим амплитудно-фазовую частотную характеристику (А.Ф.Ч.Х.) динамической системы. Модуль А.Ф.Ч.Х. представляет собой амплитудно-частотную характеристику (А.Ч.Х) динамической системы. Передаточные функции обобщенных координат у 1 , у 6 эквивалентной динамической системы лесопогрузчика, полученные в результате функциональных преобразований уравнений, получены в следующем виде [1]:

Здесь

wy 1 (s ) =

wy 6 (s ) =

2(277 (s)+ а72 )d2 (s) d 1 (s )• d 4 (s)- d 2 (s )• d 3 (s)

2(2П7 (s)+ ^ )d 1 (s) d 1 (s )• d 4 (s)- d 2 (s )• d 3 (s)

d 1 (s ) = s2 + a1 s + a 2,      d 2 (s ) = a 3 s + a 4,

d 3 (s ) = b3 s + b4,

d 4 (s ) = s2 + b1 s + b 2.

Числовые значения коэффициентов при комплексном числе s приведены в табл. 1.

Значения коэффициентов при комплексном числе s

Таблица 1

Обозначение	Класс лесопогрузчика, кН
	30 32	40 42
a i =2 n 6	0,38	0,58
a 2 = O 62	7,57	6,64
а з =2 п бШ	0,594	0,944
а 4 = Ш б 2Ш	11,84	10,805
b i =A i /A2 n 7 +l c A i /A 2 2 n 8	6,674	15,045
b 2 = O 72 +l c A l /A 2 O 82	38,096	32,098
b 3 =A i /A2 n 6	0,435	0,608
b 4 =A l /A ^W 8	7,192	7,336

После перехода от преобразования Лапласа к преобразованию Фурье, получим амплитудно-фазовые частотные характеристики динамической системы в следующем виде:

w y 1 fa ) =

M, -M,a2 + iaM. 64    3

a ⁴ — M 0 a ² + M 5 — i ( M 1 a ³ — M 2 a )

/. \ M. — M.a2 + ia-M.. — M., • ia3

w 6 fa) = —--------3---7---- y      a4 — M 0a2 + M 5 — i a3 M 1 + i aM 2

Числовые значения коэффициентов M i приведены в табл. 2.

Таблица 2

Значения коэффициентов M i амплитудно-фазовых частотных характеристик W yi ( ia), W y6 ( ia)

Обозначение	Класс 30 32 кН		Класс 40 42 кН
	W y i ( a	W y6 (ia)	W y i ( ia)	W y6 (ia)
М 0	41,982	41,982	46,948	46,9481
М 1	7,054	7,054	15,625	15,625
М 2	55,576	55,576	105,022	105,022
М 3	141,673	49,786	243,62	102,938
М 4	5,507	57,215	17,959	51,352
М 5	203,234	203,234	133,864	133,864
М 6	635,713	406,448	435,636	267,711
М 7	0	9,972	0	19,024

С целью определения энергетических спектров внешних воздействий на динамические системы лесопогрузчиков были проведены экспериментальные исследования случайных процессов X(t) взаимодействия ходовой системы и корпуса с опорной поверхностью при движении машины с упругим (хлыстами) и жестким (сортиментами) грузом. В результате корреляционного и спектрального анализа реализаций случайных процессов были определены их нормированные спектральные плотности [1]. Спектральная плотность характеризует распределение энергии колебаний по непрерывным частотам разложения. Полученные значения амплитудно-частотных характеристик динамических систем лесопогрузчиков и спектральных плотностей S x (f) процессов внешних воздействий на динамические системы X(t) позволяют перейти к вычислениям спектральной плотности случайных процессов динамических нагрузок на элементы конструкции лесопогрузчика S y (a).

В результате спектрального анализа случайных процессов x i (t ) получены нормированные спектральные плотности внешних воздействий. Поэтому при вычислении энергетических спектров динамических нагрузок на рабочее оборудование (выходных параметров) значения S x ( f) умножались на дисперсии процессов ox².

S_y i (a)= S_xi (f) •O xi² \W_yi (ia)\². (9)

Значения частоты возбуждения при скорости грузового хода 0,7–1,4 м/с (2,52–5,04 км/ч) в единицах частоты периодического процесса (Гц) и угловой частоты (с ^-1 ) приведены в табл. 3.

Частота возбуждения ю при различных значениях скорости движения V (a=2nf)

Таблица 3

V	км/ч	2,52	2,88	3,24	3,6	3,96	4,32	4,32	5,04
a	Гц	1	1,176	1,32	1,47	1,62	1,765	1,765	2,06
	с -1	6,28	7,385	8,29	9,232	10,18	11,08	11,08	12,92

Известно, что если входной процесс x(t) является нормальным и центрированным с заданной спектральной плотностью Sx(a), то установившаяся реакция на него (выходной процесс) также нормальна и цен- трирована с дисперсией ар 12 [5,7]. Распределение вероятностей нагрузок на подвеску корпуса соответствует нормальному закону [1]. Следовательно, динамические нагрузки на рабочее оборудование распределены также по нормальному закону. Исходя из этого, дифференциальную функцию распределения амплитуд нагрузок на рабочее оборудование определим по формуле [7]:

f (Pi ) =

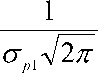
( р - р )! ^{2 а} Р 2

где р 1 — р 1 - отклонение случайной величины нагрузок р 1 от среднего значения;

а _р 1 - среднеквадратическое отклонение нагрузки р 1 .

Значения а _р 1 для рассматриваемых динамических систем определялись по формуле:

а р 1 = DpPi.

1~

Здесь Dp 1 =   j Sp1 (a)da - дисперсия процесса динамического нагружения рабочего обору- п 0

дования, равная площади под кривой спектральной плотности нагрузок p ₁ с учетом принятых масштабов по осям абсцисс и ординат [7].

На рисунке 2 представлены дифференциальные функции распределения амплитуд динамических нагрузок на рабочее оборудование лесопогрузчиков класса 25 и 35 кН в интервале ±3 o pi относительно центра группировок. В качестве центра группировок, относительно которого определялись амплитуды динамических нагрузок на элементы конструкции и значения их вероятностей, принято математическое ожидание нагрузок на технологическое оборудование, равное номинальной грузоподъемности лесопогрузчика.

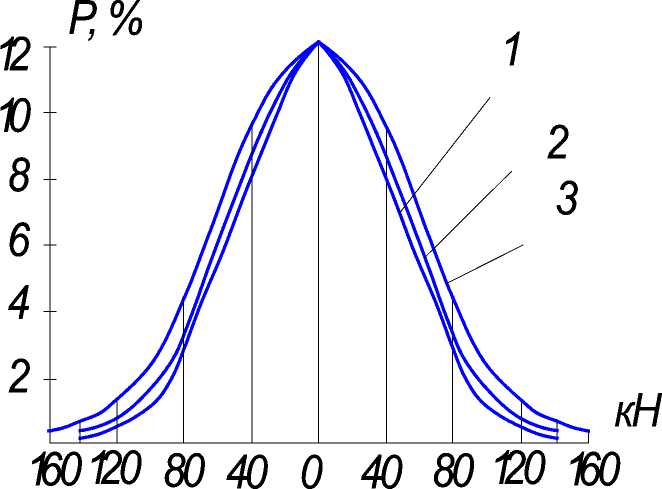
Рис. 2. Кривые распределения амплитуд нагрузок на рабочее оборудование:

1 – лесопогрузчик класса 25 кН с упругим грузом; 2 – лесопогрузчик класса 35 кН с упругим грузом;

3 – лесопогрузчик класса 25 кН с жестким грузом