Анализ динамики развертываемой космической тросовой системы с атмосферным зондом

На протяжении последних десятилетий космические тросовые системы (КТС) вызывают постоянный интерес из-за их возможных полезных применений, например, для исследования верхних слоев атмосферы [1], удаления космического мусора [2], наблюдения дальнего космоса [3]. В частности, КТС с атмосферным зондом (АЗ) рассматривалась как перспективная технология для получения научной информации об атмосфере [4]. Среди трех основных этапов (развертывание, эксплуатация и удаление из космоса), составляющих рассматриваемую космическую миссию, процесс развертывания КТС является наиболее важным для всего жизненного цикла тросовой системы [3, 5].

Рассматривается движение КТС, состоящей из космического аппарата (КА), с которого осуществляется управляемый выпуск троса, и АЗ. Атмосферный зонд это легкая металлическая или надувная конструкция по форме близкая к сфере, и имеющая сравнительно большой баллистический

коэффициент s= c_xS / m , где c_x – коэффициент лобового сопротивления, S и m – характерная площадь и масса. Развертывание КТС производится в конечное положение, близкое к местной вертикали (с учетом действия аэродинамических сил).

Отделение зонда от КА осуществляется с некоторой относительной скоростью в направлении близком к направлению местной вертикали. Анализируется возможность недопустимого увеличения угла между направлением троса и местной вертикалью (больше p/2) на начальном участке развертывания КТС. Рассматриваемый эффект может привести к запутыванию троса и к невыполнения целей космической миссии. Причиной увеличения угла отклонения троса от вертикали является довольно сложное совместное влияние моментов от действия аэродинамических сил и сил Кориолиса на начальном этапе развертывания КТС, когда стабилизирующее действие гравитационного момента невелико из-за небольшой длины троса.

Рассматривается классический метод управления движением динамических систем, когда задача управления разделяется на две подзадачи: 1) построение номинальной программы развертывания КТС; 2) применение алгоритмов регулирования для компенсации отклонений от номинальной программы, возникающих из-за действия малых возмущений (задача стабили- зации). Для построения номинального закона развертывания КТС используется математическая модель движения КТС в орбитальной подвижной системе координат [6, 7]. Особенностью данной модели движения КТС является учет аэродинамических сил, действующих на КА и зонд. Предлагается программа развертывания КТС, обеспечивающая приведение тросовой системы в положение, близкое к вертикальному (при заданной длине троса), без решения краевой задачи. Полученная номинальная программа развертывания КТС обобщает аналогичные программы [7–9], так как не накладывает ограничение на отношение масс концевых тел и учитывает действие аэродинамических сил.

Моделирование работы системы регулирования с использованием полученной номинальной программы развертывания КТС осуществляется с использованием математической модели в геоцентрической системе координат, учитывающей, растяжимость троса, инерционность механизма управления, ошибки системы отделения зонда от КА и другие возмущения, не учтенные при построении номинального закона. Концевые тела в этой модели – материальные точки, трос невесом. При растяжении трос подчиняется закону Гука с односторонней механической связью. Регулирование осуществляется по измерениям длины и скорости выпуска троса. Используется линейный регулятор с обратной связью, учитывающий ошибки реализации номинальной траектории развертывания зонда. Механизм выпуска троса аналогичен механизму, примененному в реальном космическом тросовом эксперименте YES2 [10], и работает только на торможение троса.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ В ПОДВИЖНОЙ ОРБИТАЛЬНОЙ

СИСТЕМЕ КООРДИНАТ

При записи уравнений движения КТС используется правая геоцентрическая орбитальная подвижная система координат OX_oY_oZ_o (рис. 1), где ось OX_o направлена по линии OC , здесь C – центр масс КТС, ось CY_o лежит в плоскости орбиты и направлена в сторону движения центра масс системы. Система координат OX_oY_oZ_o вращается относительно неподвижной орбитальной системы координат OXYZ с угловой скоростью и = du / dt , где u - аргумент широты (рис. 1). Орбитальные подвижные системы координат OX_oY_oZ_o и Cx_oy_oz_o отличаются только положением начала координат, так как их координатные оси параллельны. С линией, соединяющей концевые материальные точки, связана система координат Cx_ty_tz_t , определяющая ориентацию КТС относительно орбитальной системы координат Cx_oy_oz_o . Положение системы координат Cx_ty_tz_t относительно системы координат Cx_oy_oz_o определяется углами углы 9 и в (рис. 2).

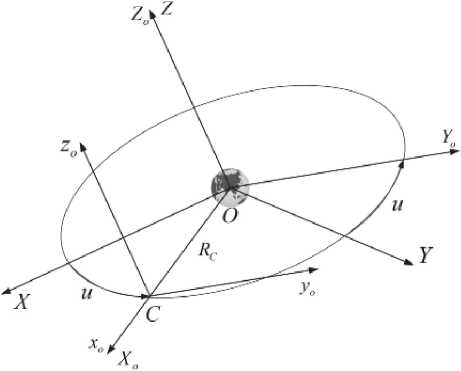
Рис. 1. Системы координат

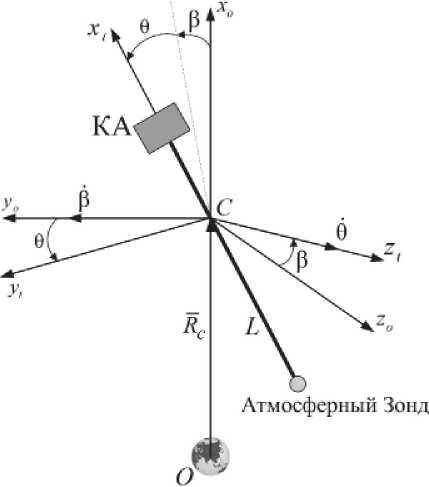
Рис. 2. Взаимное положение систем координат Cx_oy_oz_o и Cx_ty_tz_t

Построение уравнений движения в обобщенных координатах q ₁= L , q ₂=q, q ₃=b (рис. 2) методом Лагранжа проведено в работе [6], здесь L – длина троса. При получении номинальной программы развертывания КТС используются уравнения для движения системы в плоскости орбиты. Для этого случая (b=0) уравнения движения КТС принимают вид [6]

L = L [(9 + и )² - и ²(1 - 3cos² 9)] + Q^L — T n , (1) M_e

•

• 9    =- 2 L (9 + и) - ³ u ²sin29 + - Q ^, (2) L       2          M e L^

где Me=m1m2/M, m1, m2 – массы концевых точек, M = m1+m2, Tn – номинальная сила натяжения троса, QL и Qq – обобщенные аэродинамические силы. При выводе уравнений (1-2) предполагается, что орбита центра масс системы за время развертывания системы не изменяется и близка к круговой орбите.

Обобщенные аэродинамические силы опре деляются из выражений [6]

Q 9 = Q 91 ⁺ Q 92 , Q L = Q L 1 ⁺ Q L 2,    ⁽³⁾

где

Q e 1 = ^- 2 c i S i^pi V r i A L 1⁽ V i^{cos(9 -} Ф 1 ) ⁺ V ei ) , Q L1 = ^- 2 ^c 1 S 1 P 1 V r 1 mj^V sin ^{9 -} Ф 1 ) ⁺ V L 1 ) ,

Q 92 = 2c^c 2 S 2^p2 V r2 ^ L 2 (V 2 ^{cos(e +} Ф 2 ) ^- V 92 ) ,

Q L 2 = 2 ^C 2 ^S 2^p2 V r 2 2 1 ^{( V} 2 ^{sin(e +} ^ 2 ) ^- V L 2 ) ,

V_rk ( k =1,2) – вектор скорости k –ой точки относительно атмосферы, c_k – коэффициенты сил аэродинамического сопротивления, S_k – характерные площади, r _k - плотности атмосферы, V 9k = A L k 9 ,

V Lk = A L ¹ k , A L 1 = Lm 2 / M , A L 2 = Lm \ IM , V_k – скорости точек за счет вращения орбитальной системы координат OX_oY_oZ_o (переносные скорости), j _k – углы между вектором R_c (рис. 2) и радиус-векторами концевых точек в геоцентрической системе координат.

При вычислении аэродинамических сил предполагается, что они направлены противоположно векторам относительных скоростей V_rk , то есть учитываются только силы лобового сопротивления. При построении номинальной траектории развертывания КТС вращение атмосферы не учитывается, то есть абсолютная и относительная скорости не различаются.

ПРОГРАММА РАЗВЕРТЫВАНИЯ КТСВ ПОЛОЖЕНИЕ, БЛИЗКОЕ К ВЕРТИКАЛЬНОМУ

Программа развертывания КТС в положение, близкое к вертикальному, строится исходя из обеспечения конечных условий движения системы при выпуске троса на заданную длину L = L_k . Для этого необходимо рассмотреть уравнение (1) при L = L = 0 . Тогда, как нетрудно установить, система (1-2) будет иметь положение равновесия 9 = 9 = 0 , близкое к вертикальному, если силу натяжения определить из выражения

T n = M e fi² cos² 9 1 [ a ( L - L_k ) + b ^ L + 3 L k ] + Ql , (4)

где a , b - параметры закона, Q = u i , 9 1 - угол отклонения троса от вертикали, определенный из уравнения (2) при 9 = 9 = L = 0 .

Программа (4) обобщает аналогичные программы, приведенные [7-9], так как записана для произвольного соотношения масс концевых тел и с учетом аэродинамических сил. Если a>3, b>0, то система (1-2) имеет асимптотически устойчивое положение равновесия L=Lk, L = 9 = 9 = 0 (если пренебрегается изменением параметров орбиты). Доказательство этого утверждения может быть проведено по схеме, приведенной в работе [9], посредством анализа собственных значений соответствующей линеаризованной системы. Причем существует (при a=const) некоторое критическое значение параметра b* > 0 такое, что когда b > b* все собственные значения линеаризованной системы становятся вещественными и отрицательными. В это случае при приближении траектории системы к асимптотически устойчивой точке выполняются неравенства VL>0, VL < 0, L< Lk. Выполнение данных ограничений является необходимым условием для номинальной программы, так как предполагается, что устройство выпуска троса работает только на торможение и не может втягивать трос. С другой стороны при значениях параметров a, b, близких к критическим a * = 3, b = b* время развертывания на заданную длину троса уменьшается, что может быть дополнительным критерием для выбора значений указанных параметров.

АНАЛИЗ НОМИНАЛЬНЫХ ТРАЕКТОРИЙ РАЗВЕРТЫВАНИЯ КТС

Проведем сравнение номинальных траекторий развертывания КА по программе (4) без учета и с учетом действия аэродинамических на КА и зонд. Зонд представляет собой тело, близкое к сфере радиуса 1 м и массой m ₂=20 кг. При проведении численных расчетов были приняты следующие исходные данные: высота начальной круговой орбиты H =250 км, конечная длина троса L_k =30 км, коэффициенты сил аэродинамического сопротивления c_k =2,4 ( k =1,2), относительная скорость отделения зонда по местной вертикали вниз 2 м/с, параметры закона управления (4) a =4, b =5, баллистические коэффициенты КА и зонда s₁=1,257×10^-3 м²/кг, s₂=0,094 м²/кг. При моделировании использовались параметры стандартной атмосферы ГОСТ 4401–81, ГОСТ 25645.101–83.

На рис. 3 показаны номинальные траектории зонда относительно КА с учетом атмосферы (сплошные линии) и без учета (штриховые линии), когда масса КА много больше чем массы зонда ( m ₁=6000 кг).

Наибольшее отличие траекторий, изображенных на рис. 3, имеет место, когда производная по времени угла отклонения троса от вертикали меняет знак. Это соответствует моменту перехода к более быстрому торможению троса, так как по окончанию развертывания необходимо обеспечить условие V_L =0.

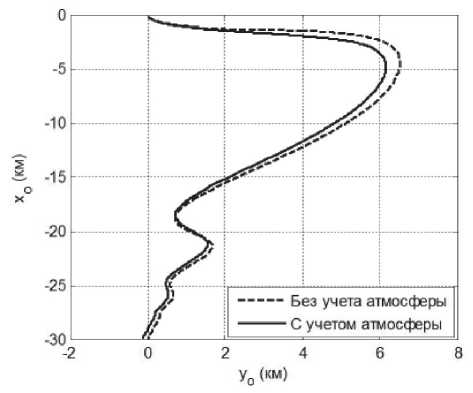
Рис. 3. Сравнение номинальных траекторий развертывания КТС, вычисленных с учетом и без учета атмосферы

АНАЛИЗ УСТОЙЧИВОСТИ ДВИЖЕНИЯ НА НАЧАЛЬНОМ УЧАСТКЕ РАЗВЕРТЫВАНИЯ КТС

Рассматривается устойчивость движения КТС относительно местной вертикали на начальном участке развертывания системы, когда длина троса сравнительно невелика. При малой длине троса стабилизирующее действие гравитационного момента уменьшается, что (при наличии аэродинамических сил) может привести к потере устойчивости движения системы, когда угол отклонения троса от вертикали становится больше π /2. Потеря устойчивости движения в этом случае может привести к столкновению КА и зонда, к ослаблению и запутыванию троса и т.д. Все это непосредственно влияет на безопасность операции и успешность процесса развертывания КТС.

Для приближенного анализа устойчивости движения введем некоторые допущения

Ф 1 ® Ф 2 ® 0, V L1 , V 61 <<  V 1 , V L 2 , V 62 <<  V 2 . (5)

Если конечная длина троса L_k несколько десятков километров, то для околоземных круговых орбит углы j₁, j₂ не превышают несколько градусов, а относительные скорости V_Lk , V _{q k} составляют меньше 0,1% от скоростей орбитального движения V_k . Кроме того, для приближенного анализа можно положить V ₁» V ₂» V_c , где V_c =W R_c – круговая орбитальная скорость центра масс.

С учетом допущений (5) уравнение (2), описывающее изменение угла θ , в безразмерной форме принимает вид

О + 2 sin 26 + F ( 6,v,g ) = 0 , (6)

где О" = d 2 6 / d т² , t = Q t - безразмерное время,

1 V c ²

2 L Q²

v =

(р1°1-р2°2 ) - безразмерный пара-

метр, sk = ckSk/mk (k =1,2), F (6,v,^) = v cos О + ц , ц = 2 - (6'+1).

Здесь безразмерный параметр m определяет действие возмущающего момента от силы Кориолиса и равен отношению момента Кориолиса к гравитационному моменту. Таким образом, динамическая устойчивость движения системы относительно положений равновесия, близких к вертикали, определяется действием возмущения F (q,n,m), которое зависит от изменения параметров КТС при ее развертывании. Причем влияние этого возмущения возрастает при малых значениях длины троса L , так как параметры n,m имеют особенность при L → 0. Это объясняется тем, что при L → 0 гравитационный момент стремится к нулю. Поэтому при анализе устойчивости движения КТС особое внимание необходимо уделять начальному участку развертывания КТС.

Анализ движения КТС на начальном участке, который следует сразу после отделения зонда от КА, показывает, что возможны два характерных случая. Эти два случая типичны и отличаются различными знаками параметра ν , который соответствует знаку момента от аэродинамических сил относительно центра масс системы. С другой стороны момент от сил Кориолиса при развертывании системы L ′ >0 всегда действует в одном направлении, противоположном угловой скорости Ω орбитального движения центра масс КТС. Поэтому наиболее опасным случаем с точки зрения потери устойчивости движения КТС при ее развертывании является случай, когда знаки параметров n, m совпадают, то есть моменты от аэродинамических сил и сил Кориолиса направлены одинаково.

На начальном участке развертывания КТС высоты, на которых находятся КА и зонд, очень близки. Поэтому ρ ₁ ≈ ρ ₂, следовательно, знак и величина параметра n определяется разностью баллистических коэффициентов Δσ = σ ₁– σ ₂. В этом случае достаточное условие устойчивости движения КТС можно записать в виде неравенства

Ao i < Ao < A^ 2, (7)

где Δσ1<0, Δσ2>0 – некоторые предельные значения разности Ac, причем |Aq2I «I^^J . Несимметричность интервала объясняется действием момента от сил Кориолиса. Предельные значения параметра Δσ можно определить только численно, если известны конкретные характеристики КТС, скорость разделения КА и зонда и т.д. Так, например, если высота круговой орбиты H=250 км, коэффициенты сил аэродинамического сопротивления ck=2,4 (k=1,2), относительная скорость отделения зонда 2 м/с, массы m1=m2=100 кг, баллистический коэффициент КА s1=1,257×10-3 м2/кг, параметры закона управления (4) a=4, b=5, то изменяя характерную площадь зонда, нетрудно определить предельные значения параметра Ас, которые равны Ас1=-2,356х10-2 м2/ кг, Ds2=6,535×10-4 м2/кг.

Если аэродинамический зонд представляет собой легкую складную конструкцию (или надувной баллон), то влияние аэродинамических сил на начальном участке развертывания можно уменьшить, раскрывая конструкцию (или надувая баллон) после прохождения опасного участка. Время формирования формы зонда можно определить, например, исходя из выполнения условия устойчивости (7).

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КТС В ГЕОЦЕНТРИЧЕСКОЙ НЕПОДВИЖНОЙ СИСТЕМЕ КООРДИНАТ

Для предварительного анализа работы системы регулирования при использовании закона (4) и для проверки некоторых допущений, принятых при построении номинальной траектории развертывания КТС, используется математическая модель движения, записанная в геоцентрической неподвижной системе координат OXYZ (рис. 1). Уравнения движения концевых материальных точек записываются в виде [9]

^dRk — v     т ^dVak —     । т । d    /о\

- Vak , m k _d(_t ~ Gk + T k + R ak , (8)

где R_k ( k =1,2) – радиус-вектора КА и з о нда , V_{a k} – абсолютные скорости концевых масс, G_k , T_k , R_ak – вектора гравитационной сил, сил натяжения троса и аэродинамических сил.

В случае центрального поля притяжения имеем

G ₌_ Km k RL ^R k ³

где K – гравитационный параметр Земли.

Так как трос не воспринимает сжимающих усилий, то модуль силы упругости вычисляется по закону Гука

T = ^

cr

I R 1 ^- R 2| ^- L

L

,

if R 1 - R 21

^^^^^^^B

, if R 1 - R 2|

-

L >  0

,(10)

L <  0

где L – недеформированная длина троса, c_r = E×A – коэффициент жесткости, E – модуль Юнга, A =p× d ²/4– площадь поперечного сечения троса, d – диаметр троса.

Соответственно в векторном виде силы на-

тяжения троса определяются выражениями

T 1

= T R 2 ^- R 1

I R 2 ^- R 1|

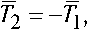
Аэродинамические силы, действующие на концевые тела, вычисляются из выражений

R ak ^- ~ c k ^p k S k V rk V rk / ² ,      ⁽¹²⁾

где V_r k ( k = 1,2 ) - вектор скорости k -ой точки относительно атмосферы.

Абсолютные и относительные скорости концевых тел связаны следующим соотношением

V rk = V ak -^ e ^x R k ,        (13)

где Q e - вектор угловой скорости вращения Земли.

При моделировании развертывания КТС к системе (8) необходимо добавить уравнения, учитывающие динамику работы механизма управления. Запишем эти уравнения в виде [9]

m e dV l = T 1 - F c , dl = V ,      (14)

dt            dt где коэффициент me учитывает инерционность механизма управления, l – нерастянутая длина троса, сошедшего с механизма управления; Vl – скорость троса. Уравнения (13) не учитывают изменение инерционности me за счет изменения массы троса, находящегося в данный момент в механизме управления.

В соответствии с принципом обратной связи силу F_c зададим в виде [10, 11]

F_c = T n + P 1 A L + p 2 А V ,       (15)

где p ₁, p ₂ – коэффициенты регулирования, T_n – номинальная сила натяжения троса, A L = l-L , A V = V l -V_L . То есть здесь осуществляется разделение управления на номинальное и поправочное управление. При работе системы регулирования, учитывается также нижнее ограничение на управляющую силу F c ³ >  F c min. При моделировании процесса развертывания КТС используется «идеальный» регулятор, то есть не учитываются ошибки измерений, дискретность управления, запаздывание отдельных элементов системы регулирования и другие возмущения, характерные для работы реальной системы управления.

В момент отделения зонда, используя закон сохранения импульса, получим скорости центра масс КА и зонда после отделения

V , 1 = V c ^- m 2- V r . V a 2 = V_a 1 + V r ■   (16)

г д е V_r – относительная скорость отделении груза, V_c – скорость центра масс системы до отделения.

МОДЕЛИРОВАНИЕ И АНАЛИЗ ДИНАМИКИ РАЗВЕРТЫВАЕМОЙ КТС

Моделирование развертывания КТС в геоцентрической системе координат позволяет оценить некоторые допущения, которые были приняты при построении номинального закона развертывания КТС. Это растяжимость троса, возможность его провисания, изменение параметров орбиты центра масс системы, различие абсолютной и

относительной скоростей при вычислении аэродинамических сил (9), наклонение орбиты.

Исходные данные, приведенные выше для анализа номинальных программ, дополняются следующими данными: инерционность механизма управления m_e =0,2 кг, модуль упругости Юнга E =2,5 x 10¹⁰ н/м², коэффициенты обратной связи p ₁=0,243, p ₂=7,824 [11], минимальная управляющая сила в механизме выпуска троса F_{c min}=0,01 н, конечная длина троса L_k =30 км.

На рис. 4, 5 показаны траектории зонда относительно КА, где номинальные траектории показаны штриховыми линии, а возмущенные траектории – сплошными линиями. Рассматриваются случаи, когда масса КА много больше масса зонда. Рис. 4 соответствует случаям, когда номинальные зависимости L ( t ), V_L ( t ) определяются без учета аэродинамических сил, а рис. 5 соответствует случаям, когда номинальные зависимости определяются с учетом аэродинамических сил. Анализ представленных результатов показывает, что использование номинальной программы развертывания КТС без учета аэродинамических сил приводит к большим ошибкам в конце развертывания, которые проявляются в колебаниях груза относительно вертикали. Учет аэродинамических сил при построении номинальных траекторий позволяет существенно уменьшить ошибки регулирования. Так, например,

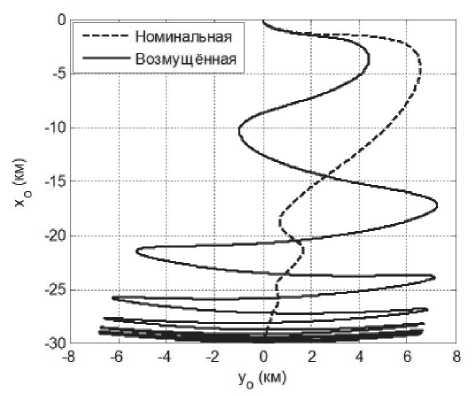
Рис. 4. Номинальная и возмущенная траектории развертывания КТС. Номинальная траектория определяется без учета аэродинамических сил (s₂=0,015 м²/кг, m ₁=6000 кг, m ₂=20 кг)

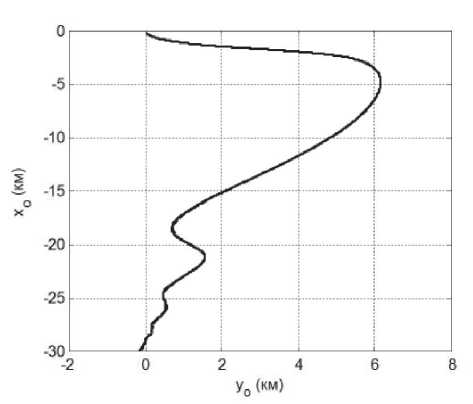
Рис. 5. Номинальная и возмущенная траектории развертывания КТС (траектории практически совпадают). Номинальная траектория определяется без учета аэродинамических сил ( s₂=0,015 м²/кг, m ₁=6000 кг, m ₂=20 кг)

для траекторий, изображенных на рис. 4 и рис. 5, ошибка регулирования уменьшается приблизительно в 36 раз. Ошибка приведения КТС в заданное состояние формируется в момент перехода к более сильному торможению троса для обеспечения краевого конечного условия по скорости V_L =0.

В табл. 1 приводится сравнение ошибок приведения зонда в конечное вертикальное положение, когда m ₁=6000 кг, m ₂=20 кг, для различных высот круговой орбиты и длин троса. Приведенные в табл. 1 результаты показывают, что во всех рассмотренных случаях наблюдается существенное уменьшение ошибок приведения зонда в заданное состояние, если номинальные программы развертывания КТС строятся с учетом действия аэродинамических сил.

Во всех рассмотренных случаях за время развертывания КТС изменение высоты орбиты центра масс системы не превышает 1 км. Учет вращения атмосферы (13) и наклонения орбиты слабо влияют на результаты, приведенные в табл. 1. Удлинение троса при длине L_k =30 км составляет приблизительно 10 м. Когда массы КА и зонда сравнимы по величине, учет аэродинамических сил при построении номинальных траекторий позволяет также существенно уменьшить ошибки регулирования.

Таблица 1. Сравнение ошибок (отклонение троса от вертикали в км) в момент окончания развертывания КТС

L k , км	H = 250 км		H = 270 км		H = 290 км
	без учета атмосферы	с учетом атмосферы	без учета атмосферы	с учетом атмосферы	без учета атмосферы	с учетом атмосферы
20	3,165	0,109	2,507	0,069	1,909	0,045
30	6,545	0,149	5,902	0,101	5,118	0,077
40	8,171	0,207	8,035	0,152	7,418	0,136

ВЫВОДЫ

На основании проведенных исследований динамики КТС с атмосферным зондом можно сделать следующие выводы:

• 1.    Начальный участок развертывания КТС является наиболее опасным с точки зрения обеспечения динамической устойчивости движения системы с учетом влияния аэродинамических сил, так как на этом участке стабилизирующее влияние гравитационного момента минимально.

• 2.    При выборе параметров КТС необходимо стремится, чтобы параметры n, m имели, по крайней мере, разные знаки, в противном случае направления действия моментов от сил инерции и аэродинамических сил совпадают, и создаются наиболее благоприятные условия для потери устойчивости движения системы на начальном участке ее развертывания.

• 3.    Использование номинальной программы развертывания КТС без учета атмосферных возмущений приводит к большим ошибкам в конце развертывания, которые проявляются в колебаниях груза относительно вертикали. Учет аэродинамических сил при построении номинальных траекторий позволяет существенно уменьшить ошибки регулирования (табл. 1). Данный вывод остается в силе при изменении наклонения начальной орбиты центра масс КТС и при учете вращения атмосферы (13).