Анализ динамики захвата клеток в оптической ловушке в приближении геометрической оптики

Для измерения сил, действующих при оптическом захвате клеток крови в капиллярах живого организма, необходимо иметь надёжные методы калибровки жёсткости ловушки [1, 2]. Наиболее распространённые на данный момент методы калибровки непригодны в условиях захвата in vivo , так как в основном данные методы предполагают осуществление либо контролируемого воздействия на частицу, либо слежения за положением частицы при помощи фотодетектора (Quadrant Photo Detector – QPD), использующего рассеянный частицей свет [3]. Оценка жёсткости ловушки в условиях захвата in vivo может быть проведена при помощи видеомикроскопического отслеживания пространственного положения клетки [4] и последующего анализа её динамики при захвате [1, 5]. Для построения динамической модели захвата клетки необходимо детально проанализировать силы, действующие на клетку при оптическом захвате.

Выделяется три класса объектов, для которых развиты различные способы расчётов, действующих в оптической ловушке сил: малые частицы, диаметр которых менее 0,1λ (приближение Рэлея), частицы промежуточных размеров от 0,1λ до 10λ и крупные частицы диаметром более 10λ (приближение геометрической оптики) [6]. Таким образом, эритроциты обладают геометрическими размерами, которые позволяют рассматривать задачу об их захвате в приближении геометрической оптики [7, 8]. Для упрощения расчётов в качестве простейшей модели клетки может быть рассмотрена микросфера с соответствующими геометрическими размерами [1, 9].

Классическая теория для расчёта сил в геометрическом приближении была развита в работах [10,11], и в настоящее время данная теория широко используется для проведения численных оценок параметров разнообразных экспериментов и построения их математических моделей [12– 16].

В данной работе разработана динамическая модель захвата микросфер размерами d>10X при их движении в широком капилляре с постоянной скоро- стью. На основе данной модели рассматриваются условия захвата микросфер в зависимости от скорости движения, мощности сфокусированного лазерного излучения и динамической вязкости жидкости. Выявлено, что максимальная скорость, при которой возможен захват, определяется вязкостью жидкости и мощностью пучка. Поэтому при известных величинах мощности и скорости может быть определена локальная вязкость жидкости, в которой движутся микросферы или клетки. При условии отсутствия захвата (при достаточно большой скорости движения) проводится анализ временной зависимости координаты центра микросфер от величины мощности излучения в сфокусированном пучке. Данный анализ может быть использован при калибровке жёсткости ловушки в условиях оптического захвата in vivo.

Для разработки динамической модели захвата проводится вывод расчётных формул пространственной зависимости действующей силы на основе рассмотрения геометрического изменения импульса фотонов [17]. Данный подход позволил проанализировать преломление лучей, принадлежащих различным квадрантам апертуры микрообъектива, а также получить в явном виде расчётную формулу зависимости силы от расстояния между центром микросферы и фокусом пучка. Отметим, что расчётные формулы классической теории формально были получены для случая слабой фокусировки пучка (то есть для фокусирующего объектива с малой числовой апертурой) [10,18]. Поэтому разделение совокупной оптической силы, действующей на микросферу, на градиентную силу и силу рассеяния, проведённое для сфокусированного пучка [11], формально не было обосновано. В данной работе на основе анализа преломления лучей выведено выражение, совпадающее с полученным ранее [11], для силы, которая может быть интерпретирована в качестве градиентной.

1.    Геометрическая модель оптической ловушки

Для вывода расчётных формул сил, действующих в оптической ловушке на объект, рассмотрим преломление лучей сфокусированного пучка микросферой. При изменении направления распространения лучей происходит изменение импульсов фотонов, которые направлены вдоль луча. Изменение импульса может быть вызвано только действующей силой со стороны сферы. Поэтому согласно III закону Ньютона на сферу действует противоположно направленная сила, которая может быть записана следующим образом [11]:

_ пР F = Q — ,

c

где Q – безразмерный коэффициент, n – показатель преломления среды, окружающей микросферу, P – мощность излучения сфокусированного пучка, размер фокуса которого много меньше размеров сферы, с – скорость света в вакууме.

Таким образом, для расчёта действующей на объект в ловушке силы необходимо вычислить безразмерный коэффициент Q , который зависит от геометрического изменения импульса, а также от изменения импульса из-за отражения лучей на поверхности диэлектрической сферы.

В классических работах [10,11] сила, действующая на микросферу, разбивается на две составляющих: силу рассеяния ( F _S) и градиентную силу ( F _G). Для каждой из данных сил были выведены соответствующие геометрические коэффициенты q S и q G , которые относятся к преломлению одного луча [11]:

= 1 + R cos 2 0-

q _S

T2 [cos(20- 20’) + R cos20]

1 + R ² + 2 R cos2 0‘      ^, (2)

T ² [ sin ( 2 0- 2 0' ) + R sin 2 01

q_r = R sin 20-- ^--- Ц--------------- ^ .     (3)

G                1 + R ² + 2 R cos2 0‘

Входящие переменные в выражениях (2) и (3) будут пояснены далее.

Дальнейшее рассмотрение преломления лучей микросферой производится при следующих приближениях:

• 1.    Сфокусированный пучок считается гомоцен-тричным, существующие при фокусировке аберрации не учитываются (степень влияния аберраций на экспериментально измеряемые силы в ловушке изложена в работе [19]).

• 2.    Размеры фокусного пятна считаются пренебрежимо малыми по сравнению с размерами объекта, что справедливо для объективов с большой числовой апертурой, используемых для осуществления оптического захвата.

В качестве материала микросферы рассматривается как полистирол (PS) c показателем преломления nS = 1,57, так и однородный диэлектрик с показателем преломления 1,4, равным показателю преломления эритроцита [20]. В качестве среды, в которой движутся микросферы, рассматриваются плазма крови и дистиллированная вода с показателем преломления, близким к плазме крови nW = 1,33 [20], но с отличной от первой среды динамической вязкостью. Выбор полистирола в качестве одного из материалов микросферы объясняется двумя причинами: во-первых, данный материал рассматривается в классической работе [11] для расчёта значений безразмерного коэффициента Q, поэтому данный выбор удобен для сравнения результатов расчётов. Во-вторых, микросферы из полистирола являются удобными объектами для отработки алгоритмов видеомикроскопического слежения при осуществлении оптического захвата [2, 4]. Различие в показателях преломления между полистиролом (1,57) и эритроцитом (1,4) [20] при расчётах приводит к уменьшению величины действующей силы, что может быть компенсировано увеличением мощности лазерного излучения до соответствующего значения. Величина данной компенсации мощности составляет в среднем 2,8 раза. Отметим, что длина волны излучения лазера λ приходится на ближний ИК-диапазон, в котором поглощение излучения эритроцитом и полистиролом невелико.

Построим схему разбиения апертуры (рис. 1) микрообъектива на квадранты, которым принадлежат преломляемые микросферой лучи, так как проекции изменения импульса после преломления лучей, принадлежащих разным квадрантам, различны [21].

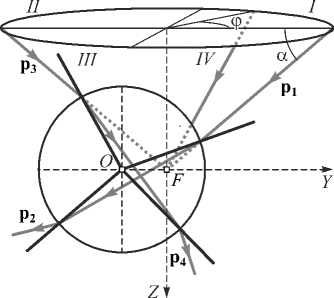
Рис. 1. Преломление микросферой лучей, принадлежащих различным квадрантам

На рис 1. введены следующие обозначения: т. О – центр микросферы, т. F – фокус пучка (центр ловушки), ось OZ – направление распространения пучка, ось OY – направление движения микросферы, углы α и φ – углы, задающие положение падающего луча относительно апертуры микрообъектива.

Из рис.1 видно, что проекции на ось OY импульсов фотонов, принадлежащих преломлённым лучам, зависят от принадлежности лучей к одной из пар квадрантов: I/IV и II/III. Этим объясняется различный вклад преломлённых лучей в итоговое изменение импульса.

Построим схему преломления луча, принадлежащего I квадранту (рис. 2), и проанализируем изменение направления его распространения после преломления.

Поясним некоторые обозначения, введённые на рис. 2: угол θ – угол падения луча, θ' – угол преломления, ОА, ОВ – перпендикуляры к поверхности сферы, ось OX перпендикулярна осям OZ и OY. Направление падающего луча задаётся вектором р 1 преломлённого луча на выходе из сферы – р 2, EG – перпендикуляр к плоскости OXY.

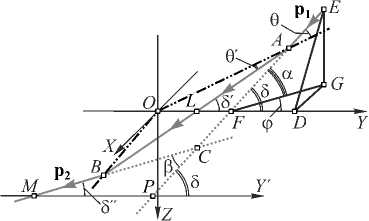
Рис. 2. Схема преломления луча, принадлежащего I квадранту

Тогда угол δ, образуемый падающим лучом и прямой OY, может быть определён из следующего условия: cos 8 = cos a cos ф .

Из треугольника ОАF, длины сторон которого равны: ОА= R – радиус микросферы, OF= S – расстояние между центром микросферы и центром ловушки, по теореме синусов: sin 6 = ( S/R )sin 8 . Именно данное соотношение определяет резкий спад градиентной силы при расстояниях, больших радиуса R , так как лучи, имеющие наибольший угол падения, перестают преломляться микросферой и, соответственно, вносить вклад в итоговое изменение импульса.

Из треугольника LAF: 8' = 8 - 6 + 6' . Из треугольника АСВ: Р = 2 ( 6-6' ) .

Проведём вспомогательную ось O ' Y' ТТ OY и из построенного треугольника СРМ: 8" = 8 - в . Исходя из построений проекция p₂ на ось OY: p_2Y =- T ( 6 )²cos( 8 - p ), где T ( 6 ) - коэффициент пропускания Френеля.

Тогда изменение импульса вдоль оси OY запишется для I квадранта в виде:

A p‘_Y = Р 2 Y — P 1_Y =- ( T ( 6 ) 2 cos( 8-P ) - cos 8 ) . (4)

Таким образом, изменение импульса A p I_Y <  0 и направлено в сторону центра сферы, поэтому F_Y >  0 , то есть F _Y ^I может быть интерпретирована как градиентная сила, которая стремится вернуть сферу в положение равновесия, при котором фокус совпадает с центром сферы.

В выражении для изменения импульса (4) учтено, что импульс преломлённого луча уменьшился из-за отражения от двух границ раздела: жидкость-микросфера и микросфера-жидкость путём умножения на коэффициент пропускания T ( 6 ).

Построение схемы преломления для луча, принадлежащего II квадранту, может быть проведено аналогично приведённой выше схеме, с учётом зеркальной симметрии отсчёта углов.

Сохраняя геометрический смысл обозначений углов для проекции изменения импульса луча из II квадранта, получим:

A p "_Y = p _{2 Y} - p_{1 Y} = T ( 6 ) 2 cos( 8+p ) - cos 8 . (5)

Таким образом, изменение импульса зависит от принадлежности луча одной из пар квадрантов. Изменение импульса, которое происходит из-за отраже- ния лучей, должно взаимно компенсироваться для зеркально-симметричных лучей. Поэтому изменение импульса лучей неодинаково для всех квадрантов, как указано в статье [11].

Сложим по модулю выражения (4) и (5) и преобразуем к окончательному выражению, описывающему изменение проекции импульса на ось OY:

A p _Y = T ( 6 ) 2 sin 8 sin p . (6)

Формула, выражающая пространственную зависимость коэффициента Q , входящего в выражение (1) и определяющего действующую силу:

n /2 n /2

Q Y ( S ) = k J J A p _Y ( а , ф , S ) d a d ф , (7) 0 n /9

где k - коэффициент нормировки, равный 1/ п . Данный коэффициент выбран исходя из равенства максимальных значений расчётных коэффициентов по формуле (7) со значениями, указанными в статье [11].

Ранее выведенная формула [11] для расчёта градиентной силы F G = q_G sin 8 , относящаяся к преломлению одного луча, совпадает с выведенными в данной работе формулами для изменения импульса A p_Y , если приравнять коэффициент отражения Френеля R ^ 0 . Как отмечалось ранее, учёт отражённых лучей не может быть проведён в отрыве от принадлежности луча одному из квадрантов.

Нижний предел интегрирования в формуле (7) по апертурному углу α выбран равным значению, использованному в работе [11]. Данный предельный угол соответствует иммерсионным объективам с числовой апертурой более 1,2 ( NA ≥ 1.2), которые применяются на практике для осуществления трёхмерного захвата различных микрочастиц [3, 13], включая клетки [1, 2].

2.    Анализ динамики захвата клеток

Анализ динамики захвата клеток строится на следующей модели: микросфера (как модель клетки [1, 5]) перемещается потоком жидкости по каналу с постоянной скоростью V0 так, что её центр находится на той же оси, что и фокус пучка (ось OY). Рассмотрение динамики захвата в плоскости, в которой лежит фокус пучка, объясняется тем, что при трёхмерном захвате в данной плоскости действующая на микрочастицу продольная составляющая FZ градиентной силы практически равна нулю, что позволяет проанализировать задачу о возможности захвата только в поперечной плоскости OXY. Если продольная сила достаточна для захвата, то во время его осуществления частица будет двигаться вдоль оси OZ до тех пор, пока не достигнет лежащей рядом с фокусом равновесной точки, что не повлияет на возможность захвата в поперечной плоскости. Аналогичное разбиение задачи о трёхмерном захвате на подзадачи, рассматривающие действующие силы в двух перпендикулярных плоскостях, производится в большинстве посвящённых данной теме работ, например, [1, 10, 11, 17, 18]. Добавим, что рассмотрение динамики движущихся вне фокуса клеток лишено смысла из-за невозможности видеомикроскопического отслеживания их динамики и осуществления таким образом экспериментальной калибровки жёсткости ловушки, один из способов которой и рассматривается в данной работе.

Зависимость силы F Y ( S )=( nP/c ) Q Y ( S ) определяется, исходя из формул (1) и (7). Скорость, при которой происходит вырывание пойманной микросферы из ловушки после её захвата, по-прежнему определяется данной возвращающей силой. Поэтому данная скорость примерно равна 100 µm/s при значениях мощности 10 mW падающего излучения. На основе данного соотношения строится один из классических методов измерения жёсткости ловушки – “drag force method” [3].

Уравнение движения имеет стандартную запись согласно II закону Ньютона [22]:

mdVdtS ) = F y ^{( 5} ) ^{+ Y} ( V — V ^{( 5} ^, (8)

где у =6 nn r - коэффициент сопротивления Стокса для сферы.

В уравнении (8) не учитывается случайная сила Ланжевена, которая характеризует броуновское движение частицы [22], так как броуновское движение частиц размерами более 10 мкм достаточно мало.

Результаты расчётов представлены ниже на рис. 3а, г, рассчитанные при различных значениях мощности падающего излучения Р, различных начальных скоростях движения микросферы V0, динамической вязкости жидкости η. Перечисленные параметры в совокупности определяют возможность захвата мик- росферы в оптическую ловушку. Радиус микросферы принимается равным 5 мкм. Рассматривается захват микросфер при условии их течения в воде и в плазме крови с соответствующими значениями динамических вязкостей: для воды – 10–3 Pa·s [22] и для плазмы крови – 1,2· 10–3 Pa·s [1]. Краевые эффекты, связанные с движением вблизи стенок канала, не учитываются (считается, что канал достаточно широкий), поэтому значения вязкости принимаются равными табличным значениям.

Критическая максимальная скорость, при которой всё ещё возможен захват микросфер, растёт весьма медленно при значительном увеличении мощности излучения в ловушке (от 1,6 µm/s при 1 mW до 7,2 µm/s при 100 mW – значения указаны в соответствующей таблице ниже).

Увеличение мощности приводит к изменению фазовой траектории из-за малости коэффициента вязкости по сравнению со значениями ускорений и скоростей, приобретаемых при захвате микросфер в ловушку. Таким образом, параметром, определяющим значение критической скорости, является динамическая вязкость среды, в которой движутся клетки. Данная зависимость может быть положена в основу нового неинвазивного метода определения локальной вязкости жидкости. Данный метод может быть основан как на отслеживании движения клетки при различных мощностях и постоянной скорости, так и на отслеживании факта захвата при постоянной мощности и изменяющейся скорости движения клеток.

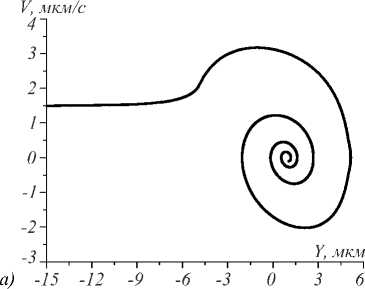
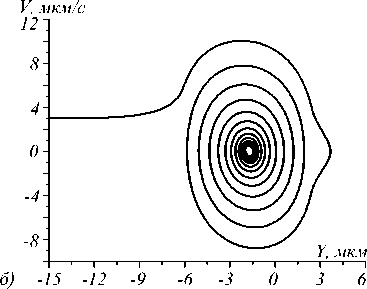
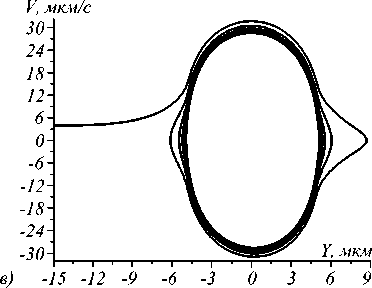
Рис. 3. Траектории захваченных микросфер с nS = 1,57 при различных условиях: (a) фазовая траектория при условии движения в потоке воды при значении мощности падающего излучения 1 мВт; (б) при значении мощности 10 мВт; (в) при значении мощности 100 мВт; (г) динамика изменения координаты центра микросферы при течении в плазме крови при различных значениях мощности и значении начальной скорости, равной 20 µm/s

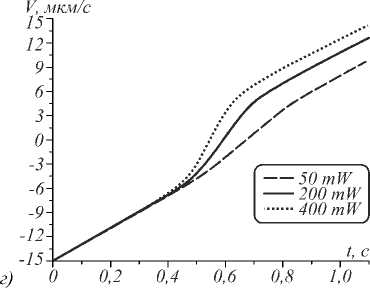
Табл. Значение максимальных скоростей

	1 мВт	10 мВт	100 мВт
При движении микросферы с nS = 1,57 в воде	1,6 µm/s	3,6 µm/s	7,2 µm/s
При движении микросферы с nS = 1,57 в плазме крови	1,7 µm/s	3,8 µm/s	7,8 µm/s
При движении микросферы с nS = 1,4 в плазме крови	1,2 µm/s	2,9 µm/s	6,3 µm/s

При учёте влияния стенок капилляра на замедление клеток (к примеру, на основе закона Факсена [23]) становится возможен захват клеток в капиллярном потоке. Поэтому для уменьшения требуемой мощности для осуществления устойчивого захвата клеток in vivo необходимо располагать центр ловушки вблизи стенки капилляра.

Рис. 3 г , характеризует динамику координаты y(t) при пролете микросферы сквозь ловушку. Из рисунка видно, что чем больше мощность падающего излучения, тем большее отклонение от прямолинейного закона изменения координаты центра микросферы вносится ловушкой. Искажение траектории клеток в капиллярах может дополнить существующие методики калибровки жёсткости ловушки in vivo [1, 5]. Отметим, что прослеживание самого изгиба в экспериментальных условиях может оказаться достаточно трудным. Несмотря на это, жёсткость ловушки или действующая сила может быть оценена по величине смещения временной зависимости координаты при постоянной скорости движения.

3.    Результаты и обсуждение

В данной работе рассмотрена динамика захвата микросферы размерами 10 мкм при её движении в жидкости с постоянной скоростью. Для построения численной модели динамики захвата была выведена в явном виде формула для расчёта зависимости силы, действующей на микросферу в ловушке, от расстояния от центра сферы до фокуса пучка. Данный вывод был построен на основе геометрического расчёта изменения импульса фотонов при преломлении на поверхностях микросферы.

Далее в работе были проанализированы условия захвата микросферы при её осевом движении относительно центра ловушки. Были рассчитаны максимальные скорости, при которых возможен захват микросферы в ловушку в зависимости от мощности падающего излучения, динамической вязкости жидкости и материала микросферы. Данная зависимость оказалась непропорциональной для различных материалов: при изменении мощности в 10 раз критическая скорость увеличивалась примерно в 2 раза (см. табл.). Таким образом, для успешного захвата клеток in vivo необходимо располагать оптическую ловушку вблизи стенок капилляра с целью создания дополнительного тормозящего эффекта, действующего со стороны стенок на клетку. Указанный эффект также может быть применён и при неосевом движении клеток относительно центра ловушки. При этом существенным различием с рассмотренным в данной работе осевым движением будет являться лишь траектория движения клетки.

Динамика движения микросферы в ловушке и возможность захвата определяется не только мощностью излучения в пучке, но и вязкостью жидкости (рис. 3 а - в ). Данный факт может быть положен в основу нового метода определения локальной вязкости плазмы крови, что позволит расширить области применения оптической манипуляции, осуществляемой in vivo [1, 2].

При отсутствии захвата оптическая ловушка вносит искажение в движение микросфер в потоке и, соответственно, в зависимость положения центра сферы y от времени t . Величина данного искажения зависит в первую очередь от начальной скорости и мощности излучения, что может быть использовано для создания нового метода калибровки жёсткости ловушки, применимого для захвата in vivo [1 – 3,5].

Для более точного рассмотрения динамики захвата клеток необходимо проанализировать пространственную зависимость силы для преломляющего объекта, который имеет форму, соответствующую клетке крови.

Работа выполнена при поддержке по госконтракту № 3.1340.2014/K конкурсной части госзадания Минобрнауки РФ и в рамках государственного задания в сфере научно-исследовательской деятельности №2014/203 НИР №1490 «Разработка оптических методов и средств контроля структуры и динамики биологических сред», а также гранта Президента РФ НШ-703.2014.2.