Анализ доминирований при многокритериальной оптимизации портфеля

Ключевые    слова:     система    управления    портфелем, многокритериальная оптимизация, доминирование по Парето, свертка критериев.

Многокритериальность задачи управления портфелем. При принятии решения о выборе той или иной системы управления инвестиционным портфелем [1] инвестор вынужден учитывать множество различных факторов и показателей. Наиболее очевидным показателем является доходность портфеля, для оценки которой используется ее математическое ожидание E . Несмотря на активное развитие современных методов и средств многокритериальной оптимизации, многие программные продукты до сих пор нацелены на максимизацию доходности портфеля. Такой подход делает выдаваемые ими результаты оптимизации особенно впечатляющими в глазах неподготовленного инвестора. Ориентация на максимальную доходность во многих случаях приводит к существенным потерям при неблагоприятном стечении обстоятельств.

Мерой возможных потерь является риск. Наиболее широко используемым критерием риска является дисперсия V доходности. Существенным достоинством этого критерия является удобство математического описания. Двухкритериальная задача оптимизации портфеля была поставлена и исследована Г.Марковицем в [2]. В общем виде ее можно сформулировать как задачу максимизации доходности и минимизации риска на множестве допустимых (доступных данному инвестору) портфелей. В подавляющем большинстве случаев эта задача имеет не одно решение (идеальную точку), а множество решений (эффективную границу), причем каждый из портфелей этого множества лучше другого по одному критерию и хуже по второму.

Дисперсия не является единственно возможным критерием риска. Различными авторами предложены и изучены альтернативные критерии – максимальная просадка капитала, квантильные критерии (точечные [3] и континуальные [4]), наихудшее время до достижения нового максимума капитала и другие. Многие из них понятны и доступны для восприятия неподготовленного инвестора, но имеют сложное математическое описание и являются статистически некорректными, что существенно ограничивает возможности их использования при формулировке и решении задач оптимального управления инвестициями.

Математическое ожидание доходности также не является единственно возможной мерой средней доходности. В качестве альтернативы часто рассматривают медиану доходности, которая является более стабильной (робастной) оценкой, но не столь удобна с точки зрения математического описания.

Кроме критериев доходности и риска, инвестор может рассматривать некоторые субъективные критерии [5], например, частоту сделок.

Таким образом, любая задача оптимизации инвестиционного портфеля (или оптимизации системы управления портфелем) является многокритериальной [6].

Для сравнения нескольких систем управления портфелями можно провести их тестирование на выборке реальных исторических данных (ретроспективное тестирование), найти значения всех критериев и некоторым образом сравнить результаты.

Сравнение векторов критериев. Обозначим вектор значений критериев i -ой системы управления инвестиционным портфелем на через cⁱ =( cⁱ 1 , cⁱ 2 ,…, cⁱ M ), где M – количество критериев. Абстрагируясь от содержательной стороны критериев, будем полагать, что увеличение значения критерия соответствует улучшению портфеля при постоянных значениях остальных критериев (критерий строго возрастает по предпочтению инвестора). Некоторые критерии (например, дисперсия доходности) в своей исходной формулировке не соответствуют данному требованию. Эту проблему можно разрешить с помощью следующих несложных преобразований:

• 1.    Если изначально лучший портфель соответствует меньшему значению критерия, то необходимо взять этот критерий с противоположным знаком.

• 2.    Если изначально у критерия есть некоторое оптимальное значение, то необходимо рассматривать отклонение от этого значения.

Если существует необходимость выбрать лучшую из нескольких систем, то для этого достаточно сравнить их все попарно. Для удобства описания далее рассматривается вопрос сравнения двух систем.

Первая альтернатива доминирует по Парето вторую альтернативу, если первая по всем критериям не хуже и хотя бы по одному лучше, чем вторая. Определим понятие доминирования по Парето применительно к паре векторов критериев, полученных на одной выборке. Будем называть вектор

1 2 С ¹ ^p C 2 1

c доминирующим вектор c ( ^P ), если все значения критериев c не меньше соответствующих значений c ² и хотя бы одно значение строго больше:

[ c ¹ >  p c 2 ]o [ v m , c m >  c m з m : c m ₀ >  c m ]

.

Выражение (1) определяет на множестве всевозможных пар векторов значений критериев бинарное отношение предпочтения (доминирования по

Парето ^ P ).

Наличие между c1 и c2 отношения доминирования по Парето дает возможность однозначно выбрать лучший из векторов, основываясь лишь на знании о строгом возрастании всех критериев по предпочтению инвестора.

Если для некоторого вектора не найдется ни одного доминирующего, то такой вектор называется недоминируемым. Задача выбора между двумя недоминируемыми векторами не имеет очевидного решения: один из векторов лучше по одним критериям, а другой – по другим.

Наиболее очевидным выходом из подобной неопределенной ситуации представляется формирование агрегированного критерия, ставящего в соответствие каждому вектору cⁱ такое действительное число A ( cⁱ ), чтобы большему значению A ( cⁱ ) соответствовал лучший вектор cⁱ .

Простейшим агрегированным критерием является линейная (аддитивная) свертка критериев [7, стр.59]: M

^Ал ( c i )

У « m c m , ^a m >  ⁰

m = 1                  .                             (2)

Коэффициенты a m характеризуют (хотя и не совсем корректно) важность [8] того или иного критерия для инвестора. При построении критерия следует иметь в виду, что критерии cⁱ m , а вместе с ними и коэффициенты a m , могут иметь разную размерность. Кроме того, при использовании линейной свертки неявно предполагается, что нормы замещения одного критерия другим постоянны и не зависят от значений критериев. Например, предполагается, что за получение 1 дополнительной единицы по критерию c i 1 инвестор готов заплатить потерей a 1 / a ₂ единиц по критерию cⁱ ₂ при любых фиксированных значениях остальных критериев. Это предположение обычно можно приближенно принять при малых изменениях значений критериев, но практика показывает, что значения критериев меняются в широких пределах.

Мультипликативная свертка является произведением значений всех критериев, возведенных в степени в m , характеризующих важность критериев:

A M ^{( c}i ) = n( ^cm ^)в m ’ в m > ⁰ m ^{= 1}                   .                            (3)

При использовании мультипликативной свертки предполагается, что все значения критериев положительные (этого нетрудно добиться переносом нуля на шкале критерия). Нормы замещения не являются постоянными. Если значение критерия плохое, то для компенсации даже небольшого его ухудшения требуется существенное улучшение по другим критериям. При этом аналогичное ухудшение хорошего значения критерия приводит лишь к небольшому уменьшению значения свертки. Таким образом, при использовании мультипликативной свертки, основное внимание уделяется "провальным" значениям критериев.

Еще одним вариантом свертки критериев является свертка Гермейера [7, стр.60]:

A r ^{( c} i ) = min Y m c m , Y m >  0 m

.

Свертка Гермейера позволяет оценить весь вектор по худшему из значений критериев.

Анализ зависимости агрегированных критериев. Доминирование по Парето является достаточным (но не необходимым) условием превосходства по любому из представленных агрегированных критериев (2), (3) и (4):

c ¹

> P c ²

^Ал ^{( c} ) > A л ^{( c} )> ■   a m ( c ) > a m ^{( c}i ) ,

A r ( c i ) ^ A r ( c i )•

Соответственно, критериям является

превосходство по представленным агрегированным необходимым, но не достаточным условием доминирования по Парето.

Опишем противоречие агрегированных критериев друг другу. Сначала рассмотрим линейную и мультипликативную свертку в двухкритериальной задаче. Зафиксируем вектор c1=(с11,с12) и найдём множество C2– векторов c2=(с21,с22), при котором наблюдается противоречие этих агрегированных критериев:

^[ c 2 G C ² - ^] ^ [ ( A л ( c ^{2 )-} A л ( с 1 ))( A м ( c ^{2 )-} A м ( с 1 )) < ^{o ]} .

С ²⁺,  на котором

приравняв к нулю

Аналогично, можно определить множество противоречие отсутствует:

c ² G C 2 'M A л ( c 2 ) - А л ( с 1 ))( A M ( c ² ) - A M ( C )) > 0 ] .

Очевидно, границу множества можно найти, произведение из (6) и (7):

( А л ( c 2 ) - A л ( с 1 ))( А м ( c ² ) - a m ( с 1 )) = 0 .

Отсюда:

A л ^{( c 2} ) = A л ^{( с 1} ) или A M ^{( c 2} ) = A M ^{( c 1} ) .

Следовательно, границами множеств С2+ и C2– являются линии уровня агрегированных критериев. Этот вывод можно распространить на любую другую пару агрегированных критериев. На рис.1 представлены различные варианты множеств С2+ (белые области) и C2– (серые области) для всевозможных сочетаний рассмотренных критериев. Наибольшее расхождение (серая область на рис.1) наблюдается между линейной сверткой и сверткой Гермейера. При малых отклонениях от c1 расхождение между линейной и мультипликативной свертками невелико, но быстро возрастает с ростом отклонения. Расхождение между мультипликативной сверткой и сверткой Гермейера при малых отклонениях больше, чем в предыдущем случае, но с ростом отклонения увеличивается не столь быстро.

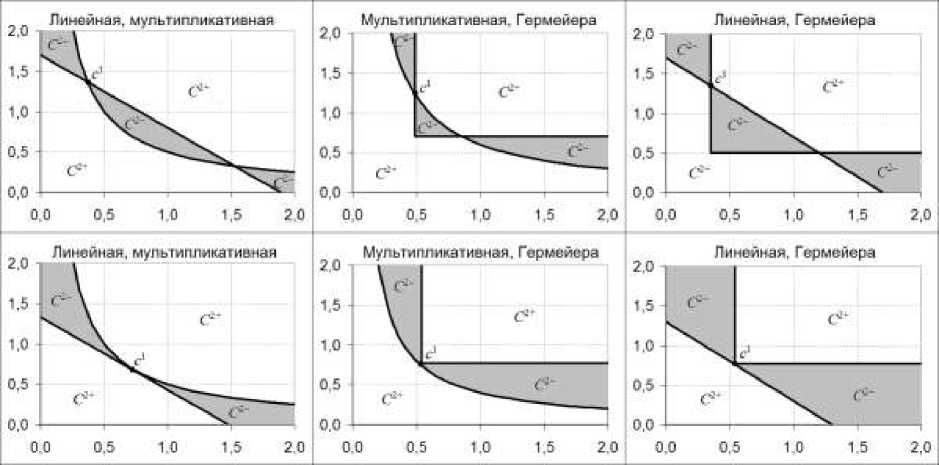
Рис.1. Множества согласия и противоречия агрегированных критериев

Используемые статистические данные и результаты моделирования. В настоящей работе проводится статистическое исследование, цель которого состоит в получении вероятностных оценок согласия и противоречия между различными видами агрегированных критериев. Рассматривались портфели, составленные из 10 наиболее ликвидных акций российского фондового рынка за 2014 год: Сбербанк, Газпром, Лукойл, ВТБ, ГМКНорНик, Магнит, Роснефть, Сбербанк-п, Сургутнефтегаз-п, МТС.

В ходе эксперимента была смоделирована динамика изменения цен двухсот различных портфелей, случайным образом составленных из акций перечисленных эмитентов. В качестве частных критериев были выбраны критерии модели Марковица: математическое ожидание и дисперсия однодневной доходности. Частные критерии были нормированы таким образом, чтобы все значения укладывались в диапазон от 0 до 1, а возрастание значения критерия соответствовало улучшению портфеля. Каждый из 200 портфелей сравнивался со всеми сгенерированными портфелями, что дало 40000 пар портфелей. Доминирование по Парето наблюдалось в 30270 парах, несравнимыми по Парето оказались 9730 пар. Использование агрегированных критериев определило доминирование во всех 39800 парах, составленных из разных портфелей (в остальных 200 парах портфель сравнивался сам с собой).

Анализ противоречий. В ходе исследования было рассчитано количество совпадений и противоречий между установленными по разным критериям предпочтениями в парах портфелей.

Формула (5) получила свое экспериментальное подтверждение – ни одного противоречия между доминированием по Парето и агрегированными критериями не выявлено. В то же время, введение агрегированных критериев позволило установить отношение предпочтения в 9528 парах портфелей (23,8%), которые являются несравнимыми по Парето.

Наибольшим является количество противоречий между отношениями предпочтения, установленными с помощью линейной свертки и свертки Гермейера – 3460 пар портфелей (8,7% от общего количества пар портфелей или 36,3% от количества пар, несравнимых по Парето). Несколько меньше противоречий между мультипликативной сверткой и сверткой Гермейера – 2988 пар портфелей (7,5% и 31,4%, соответственно). Наименьшее количество противоречий дают линейная и мультипликативная свертки критериев – 472 пары портфелей (1,2% от общего количества и 5,0% от несравнимых).

Заключение. Проведенный анализ показал, что:

• 1.    Наличие в паре инвестиционных портфелей доминирования по Парето гарантированно приводит к доминированию по всем рассмотренным агрегированным критериям. Данное утверждение обосновано теоретически и подтверждено статистически.

• 2.    Доминирование по Парето наблюдается примерно в 7580% случаев доминирования по агрегированным критериям.

• 3.    Наличие в паре портфелей доминирования по одному из агрегированных критериев с большой вероятностью (90-98%) приводит к доминированию и по другим агрегированным критериям.

• 4.    При отсутствии доминирования по Парето вероятность противоречий между агрегированными критериями существенно возрастает и составляет от 5% (линейная и мультипликативная свертки) до 36% (линейная и свертка Гермейера).

Проведенное исследование показало высокую степень зависимости между некоторыми агрегированными критериями. При оптимизации реальных портфелей замена мультипликативной свертки линейной сверткой не оказывает существенного влияния на результат, но существенно упрощает процесс оптимизации.

Полученные результаты могут найти применение в системах управления, как индивидуальными, так и коллективными инвестиционными портфелями [9], а также при построении систем обучения для начинающих инвесторов [10].