Анализ двойственных систем H2/M/1 и /M/H2/1

В настоящее время не существует аналитических методов для точного определения характеристик СМО общего вида G/M/1 или G/M/m, в отличии от СМО общего вида M/G/1, для которой известна формула Полячека-Хинчина. В таком случае, перспективным на взгляд автора является такой подход к анализу систем G/M/1, когда в качестве входного распределения G будет использована вероятностная смесь двух экспоненциальных распределений, то есть гипер-экспо-ненциальное распределение Н2. При этом СМО с гиперэкспоненциальными входными распределениями в отличие от систем с более сложными с распределениями типа Вейбулла или гамма по- зволяет получить решение задачи в аналитическом виде.

В работах [1-4] приведены полученные автором результаты для времени ожидания в системе Н2/M/1 и их практические приложения. Так же приведено преобразование Лапласа-Стильтеса для функции плотности времени ожидания для системы Н2/M/1, полученное через решение интегрального уравнения Линдли методом спектрального разложения [5]. В работе [6] приведены известные эвристические формулы для систем Н2/M/1:

Р^-р) Р где промежуточные параметры связаны с начальными моментами распределения интервалов входного потока:

p(q-r)-(q-r²) . ~ т\ . t²

W"D ’ ' б(г2У 6(f,)='

а           – начальные моменты до третьего порядка интервалов между поступлениями требований в систему. В (1) ρ означает коэффициент загрузки системы. Выражение (1) получено с помощью преобразования Лапласа-Стилтьеса функции распределения и это преобразование приведено также в [5].

Постановка задачи

В статье ставится задача качественного и количественного сравнения результатов для двойственных систем Н2/M/1 и M/Н2/1 по среднему времени ожидания в очереди. При этом системы называются двойственными, если закон распределения входного потока у одной (первая позиция в трехпозиционной системе Кендалла) меняется местами с законом обслуживания другой системы (вторая позиция в трехпозиционной системе Кендалла). Так, в системах Н2/M/1 и M/Н2/1 закон распределения входного потока Н2 у первой системы становится законом обслуживания для второй системы. Для проведения сравнительного анализа приведем решения для обеих систем.

Решение для системы Н2/М/1

В системе Н2/М/1 время поступления требований в систему задана функцией плотности преобразование Лапласа которой имеет вид

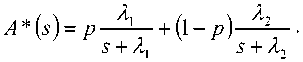
Время обслуживания имеет функцию плотности а ее преобразование Лапласа

5 + Ц

Выражение для спектрального разложе- ния решения интегрального уравнения Линдли для системы

Н2/М/1 примет вид:

/Gj      s(s2-/,s-/0) s(s + о-] )(s - о"2)

^_(s) (5 — Я, ХЛ — sXp + ⁵) (^ — Я, )(Я₇ — s)(//+ s)

где                        – отрицательный корень,                        – положительный корень многочлена             с коэффициентами                             и

/| = Я, + Я_э — ц [ 1 ] •

По правилам метода спектрального разложения решения интегрального уравнения Линдли, строим рациональные функции и

Опуская математические выкладки, запишем их

/ч s(s +СТ,) /X (s-zj^-s) вид:

5 + р              S-CT₂

Далее определяем преобразование Лапласа для функции плотности времени ожидания:

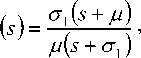
а через него, найдя значение производной при s = 0, определим среднее время ожидания в очереди:

W = 1/0-, -\/р.

где

Из прямого преобразования Лапласа (6) можно извлечь больше информации, чем только сред- нее время ожидания, а именно: выделив из выра- жения

целую часть, получим функцию плотности:

ц

где

– импульсная функция в начале координат. Автором установлена идентичность выра- жений (7) и (1), хотя эти результаты получены с помощью разных подходов. Отсюда следует, что среднее время ожидания в системе Н2/M/1

существенно зависит от трех первых моментов распределения интервалов между соседними требованиями во входящем потоке. В этом можно убедиться на примерах расчетов для системы Н2/M/1, приведенных ниже в таблице 1.

Решение для системы М/Н2/1 и его сравнение с формулой Поллячека-Хин-чина

В этом случае функция плотности распределения для интервалов поступления имеет вид

«(/) = Яе

а для времени обслуживания

6(0 = P^~^W + (1 - pV*" .     (9)

Преобразование Лапласа функции (8)

имеет вид                а функции (9) – s + A

B*^ = p—^ —н(1-р)——— s + p_x         s + p^

Тогда спектральное разложение

A *(-s)-S*(s)-l = ^₊0)/ s^ для распределений (8) и (9) с учетом их преобразований Лапласа будет иметь вид [1]:

4/ДА ^(s² +/7_|S + /7_O)         5(5 + ", )(s + -₂ )

^- (s) (A -$Xp_x + sXp₂ + s) (A- sXp_x + .vXa₂ + 0

где два различных действительных отрица тельных корня = -(/7, / 2 -7^74^) , - z₂ = -(h_x / 2 + ^hf^-A) относятся к многочлену s² + h_xs + h₀ с коэффициентами 6₀ =№_- 4(¹" РЖ + PPi 1 и h_x = p_x + p₂- X.

Опустив промежуточные выкладки, запишем выражение для среднего времени ожидания j|- _ Z, + ^.2 _ px + p2

-1^2 ЖЖ

где корни - z_x = -(A, /2 - 7a,²/4-A₀ ) и — z₂ = —(/?! /2 + _л/ h² /4 — Л_о ) соответствуют многочлену s² +h_xs + h₀ с коэффициентами ^=РхРг -^-P^Px +^₂] и h_x = p_x + p₂ - A .

Сравним полученное решение (10) с формулой Поллячека-Хинчина. По формуле Виета имеем h_x = z_x + z₂ = ц_хА- ц₂— X и /z₀ =z_x-z₂ = p_xp₂ -A^l-p^p.^pp^- Тогда формула (10) для среднего времени ожидания принимает вид

- ₌ z_x + z₂ _ p_x +p_{2 =} p_x+p₂-A _ p_x + //₂ ,

2,2, p_xp₂ p_xp₂-A\A\-p^p_x^pp^ ц_хц_г

Средняя интенсивность обслуживания в системе М/Н₂/1 есть p = a---;—=----- ’ тогда

^[(1 P^M\ + PPi\ коэффициент загрузки                      а второй начальный момент времени обслуживания _ 2(1-pX +lpp2 Отсюда после мате матических преобразований последнего выражения, получим

2(1 -pV

что полностью совпадает с формулой Полячека-Хинчина для системы М/G/1 [1].

В последней формуле λ – интенсивность входного потока, ρ – коэффициент загрузки системы, r² – второй начальный момент времени обслуживания. Заметим, что в этом случае решение не зависит от третьего момента, а полностью зависит только от первых двух начальных моментов времени обслуживания. В этом заключается качественная разница между двумя двойственными системами Н₂/M/1 и M/Н₂/1.

Сравнительные расчеты среднего времени ожидания для систем Н2/M/1 и M/Н2/1

Для того, чтобы лучше оценить количественную разницу между рассматриваемыми двойственными системами, проведем для них вычислительные эксперименты для среднего времени ожидания по формулам (1), (7) и (11) соответственно. Выше было отмечено, что формулы (1) и (7) дают идентичные результаты.

При этом для системы Н₂/M/1 в качестве входных параметров возьмем коэффициент загрузки ρ, коэффициент вариации интервала между требованиями входного потока C^ и в качестве третье го мо ме нта – коэффициент асимметрии 4_$ = (t ² - 3 • T² • t_x + At₂ ) / <з³_л, так как он содержит три начальных момента распределения интервала между требованиями входного потока. Заметим, что для экспоненциального закона распределения ^sA = 2.

Для системы M/Н₂/1 входными параметрами будут коэффициент загрузки ρ и коэффициент вариации времени обслуживания с_ц. Для удобства вычислений примем нормированное время обслуживания в обеих системах Ъ =P^{X =1}- Кроме того, расчеты проведем для случаев малой загрузки системы ( ρ = 0,1), средней загрузки ( ρ = 0,5) и высокой нагрузки ( ρ = 0,9).

Здесь ρ – коэффициент загрузки, ^CX ^и 5 - коэффициенты вариаций интервалов поступления и обслуживания. В таблице 1 коэффициент асимметрии ■^sX задан в качестве момента третьего порядка для системы Н₂/M/1 соответствующим диапазоном изменения. Например, запись (4;18) означает, что параметр 4_S. варьируется от 4 до 18. Этим лучше демонстрируется зависимость среднего времени ожидания от третьего момента. Соответственно, и результат W для системы Н₂/M/1 будет отображаться в виде соответствующего диапазона. Результаты расчетов, приведенные в таблице 1, хорошо согласуются с данными [9].

Таблица 1. Расчет среднего времени ожидания для систем Н2/M/1 и M/H2/1

Входные параметры для систем				Среднее время ожидания W
р	сх	AsX	сц	Н2/М/1	М/Н2/1
0,1	2	(4;18)	2	(0,34;0,13)	0,28
	4	(7;18)	4	(1,26;0,17)	0,94
	6	(10;18)	6	(3,79;0,24)	2,06
0,5	2	(4;18)	2	(3,14;1,23)	2,5
	4	(7;18)	4	(13,6;2,34)	8,5
	6	(10,18)	6	(32,1;7,6)	18,5
0,9	2	(4;18)	2	(23,5;18,3)	22,5
	4	(7;18)	4	(82,6;67,8)	76,5
	6	(10;18)	6	(182;165)	166,5

Заключение

Основная характеристика для систем массового обслуживания – среднее время ожидания в очереди, так как все остальные характеристики: время задержки, средняя длина очереди, количество требований в системе и др., являются производными от основной характеристики. Результаты по среднему времени ожидания в очереди для систем Н2/M/1 и M/Н2/1 получены одним и тем же методом – методом спектрального разложения решения интегрального уравнения Линдли [1]. Эти данные показывают, насколько отличаются эти две двойственные системы. Точное решение для первой системы зависит от трех моментов распределения интервала входного потока, а для второй системы – только от двух первых моментов времени обслуживания.