Анализ физических и математических моделей напряженных магнитоанизотропных структур
Автор: Дубинин А.Е., Дубинин А.А., Ахмадуллин Ф.Р.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4 т.22, 2020 года.
Бесплатный доступ
Рассматривается анализ физических и математических моделей напряженных магнитоанизотропных структур (НМАС), в котором физические модели представлены в виде ферромагнитной прямоугольной пластины или четверти кольцевого элемента (ЧЭ) в электромагнитном поле при силовом воздействии. Их математические модели описываются системами дифференциальных уравнений теорий электромагнитного поля, ферромагнетизма и упругости в декартовых, цилиндрических и сферических координатах. Показано, что наиболее полно отражается картина в НМАС в сферических полярных координатах, что подтверждено экспериментально.
Напряженная магнитоанизотропная структура, физические модели, математические модели
Короткий адрес: https://sciup.org/148312672
IDR: 148312672 | УДК: 621.318.134 | DOI: 10.37313/1990-5378-2020-22-4-86-91
Текст научной статьи Анализ физических и математических моделей напряженных магнитоанизотропных структур
В настоящее время напряженные магнитоанизотропные структуры (НМАС) находят широкое применение не только в устройствах сбора и обработки информации, но и в качестве многофункциональных устройств (МФУ): преобразователях силы, момента и перемещения; модуляторах, ключах и переключателях; регулируемых линиях задержки; акселерометрах и др. [1-7].
В связи с этим возникает актуальная задача оценки эффективности существующих физических и математических моделей НМАС при разработке различных МФУ.
Принципиальная базовая схема неуправляемых и управляемых НМАС этих устройств выполнена из двух кольцевых ферромагнитных элементов ЧЭ1 и КЭ3 (чувствительного и компенсационного, рис. 1) по дифференциально-трансформаторной резонансной схеме (обмотки возбуждения 5, 8 соединены последовательно-согласно и к генератору 2, а обмотки измерительные 4, 9 соединены последовательно-встречно и через конденсатор 6 с регистратором 7 и обмотки управления 10).
Математическая реализация такой кольцевой физической модели НМАС в трехмерном
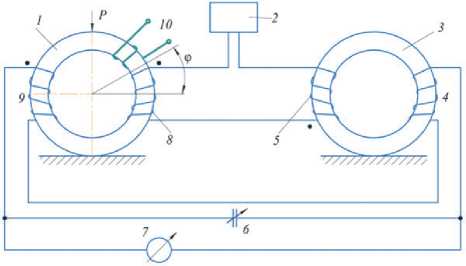
Рис. 1. Принципиальная базовая схема НМАС пространстве вызывает непреодолимые трудности из-за сложности распределения электромагнитного и силового полей в кольцевом ЧЭ. Для упрощения обобщенной физической модели кольцевого ЧЭ его неуправляемая и управляемая НМАС была представлена в двухмерном пространстве в виде прямоугольной пластины из ферромагнитного материала, равной сечению кольцевого элемента, при силовом воздействии в электромагнитном поле (рис. 2) [1-3].
При этом вводятся следующие допущения [1, 2]:
1. Магнитное поле ЧЭ изменяется по синусоидальному закону; 2. Магнитное поле равномерное и имеет нормальную составляющую магнитной индукции Bz; 3. Комплексная магнитная проницаемость ЧЭ для заданного цикла перемагничивания постоянна; 4. Плотность токов по толщине пластины не изменяется; 5. Тангенциальные составляющие напряженности электрического поля Еа и Ев на границах пла- стины постоянны; 6. Поля, идущие в обход пластины, относятся к полям рассеивания; 7. Среда пластины изменяется под действием силы; 8.
Механические напряжения в пластине имеют нормальную составляющую σ и действуют в нормальной к пластине плоскости.
При введенных допущениях обобщенная физическая модель неуправляемой НМАС ЧЭ описывается системой дифференциальных уравнений теорий электромагнитного поля, ферромагнетизма и упругости в декартовых ко- ординатах [1-3].
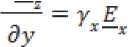
эн
—я
ЭЕ дЕ
\ --~ — --~ = ]ШЦ Н ;
Эх ду'
дБ 1
--Я я энн эн
--Я --Я я dw dP(t) 1 Е— ==
^ dz dS
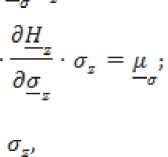
где γx и γy – удельные электрические проводимости по x и y; Ex, Ey, Hz – комплексы действующих значений напряженностей электрического и магнитного полей на поверхности пластины по осям x, y, z; ω – круговая частота поля; w – деформация НМАС; S – площадь сечения пластины; μσ=μн-∆μ – магнитная проницаемость под действием σ [1-7]; μн – начальная магнитная проницаемость; ∆μ – изменение магнитной проницаемости.
Граничные условия имеют вид:
| HSG) при ж = +а;
V 0 при х = +Ь.
Г Н^х) при у = +Ь;
V О при х = +а.
где ℓ=2a, t=2b – толщина и ширина пластины; с – длина пластины; σ – нормальные механические напряжения в пластине при действии силы P на поверхности S.
Решение дифференциальных уравнений (1-5) с условиями (6-7) осуществляется в результате анализа магнитного и электрического состояний напряженной магнитоанизотропной структуры (НМАС) ЧЭ с учетом уравнения
(5) закона упругости. В результате определены электрические и магнитные параметры НМАС и характеристики преобразователей [1-3]. Разработана физическая модель управляемых НМАС для магнитоанизатропных ключевых элементов (МКЛ) (рис. 2), выполненных по дифференциально-трансформаторной схеме [1-3].
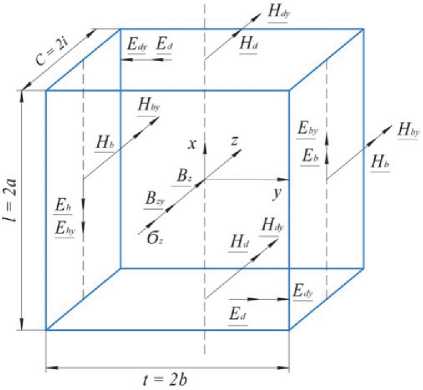
Обобщенная физическая модель управляемой НМАС также представлена в виде ферромагнитной пластины в электромагнитных полях возбуждения и управления при статическом силовом воздействии (рис. 2) при вышеназванных допущениях [1-3].
Eth- Ej
У н»
Ни / t = 2b
Рис. 2. Обобщенная физическая модель неуправляемой при E y=0 и H y=0 и управляемой при E y≠0y и H y≠0y НМАС
Физическая модель на рис. 2 с учетом принятых допущений в двухмерном пространстве при одновременном воздействии силового поля и полей возбуждения и управления описывается следующими дифференциальными уравнениями в декартовых координатах для МКЛ [3].
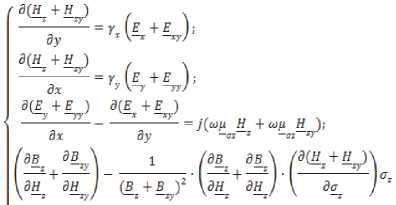
Е*^ = а,, где γx и γy – электрические проводимости по x и y; Ex, Ey, Exy, Eyy – напряженности электрических полей от возбуждения и управления по осям x, y; Bz, Bzy – магнитные индукции обмоток возбуждения и управления; ω, ωy – круговые частоты полей возбуждения и управления; σz – нормальные механические напряжения в НМАС; μσz – магнитная проницаемость от механических напряжений σz; E – модуль упругости; – деформация точки структуры по оси z.
Граничные условия при этом имеют вид:
| Hz(y) при x = +a;
НДх, — \Hn при x = +a: у = 0:
к 0 при x = +b.
Г H„(y) прих = ±a;
Hiy(x,y) = л HQ при x = fa; у = 0; (12)
к 0 прих = +b.
f ^ZGD ПРИ x = i^;
//z(x,y) = л Hb прих = +b;x = 0;
к 0 при x = +a.
Г H^GD прих= ±b;
/fzyG,y) = ) Hb при x = +b;x = 0; (13) к 0 при x = +a.
/ 0 при t < tt;
^-VG) = при
tt
( 0 при t > t2.
f 0 при t < tt;
«zvG0=]« npHt1 I —zmax ( 0 при t > t2. где a и b – размеры пластины; t – время срабатывания МКЛ; t1 и t2 – время включения и выключения МКЛ. Решение уравнения ферромагнетизма (11) известна в литературе и его решение имеет вид [1-3]: и — и = и — ^u + Ди — и + Ди = Ди , г к "у г н "а "у г н "а "у' где μу и μк – магнитные проницаемости управляемого и компенсационного элементов; ∆μσ– изменение проницаемости. Решение матмодели (8-11) с условиями (1214) осуществляется так же как и предыдущей и позволяет определить электрические и магнитные параметры управляемой НМАС и определить выходную характеристику МКЛ [1-3]. Рассмотренные физические и математические модели НМАС устройств контроля не полностью отражают суть процессов, происходящих в НМАС кольцевых ЧЭ, так как рассматриваются в двухмерном пространстве. Поэтому была разработана физическая модель НМАС в виде реальной кольцевой структуры [4-7]. Обобщенная физическая модель неуправляемой и управляемой НМАС ЧЭ сжатия и растяжения представлена на рис. 3 в виде четверти ферромагнитного кольца, сечение которого ориентированно в сферической системе полярных координат таким образом, чтобы вектор нормальных напряжений σ совпадал с направлением магнитного поля Hc, а вектор касательных напря- жений τ был с ним перпендикулярен, где P – сила воздействия на кольцо, направленная по радиусу ЧЭ под прямым углом к полю Hc; a = rн – rв; rн и rв – наружный и внутренний радиусы кольца; а – толщина кольца; b – ширина кольца; r0 – средний радиус элемента; φ – угол между осью симметрии сечения и радиусом rв; Er и Eв – напряженности электрического поля на гранях сечения; Bс – максимальная магнитная индукция внешнего магнитного поля; Hс – напряженность магнитного поля перпендикулярная сечению кольца; i – ток в обмотке возбуждения; iв – вихревой ток; iy – ток управления; θ – угол между осью симметрии сечения и радиусом r0 по длине кольца в рад. Рис. 3. Физическая модель НМАС обобщенная при iу=0 и iу≠0, τ=0 и τ≠0 Математическая модель неуправляемой НМАС ферромагнитного ЧЭ описывается уравнениями теории электромагнитного поля, ферромагнетиз -ма и упругости. Решение этой модели в трехмерном пространстве связано с большими трудностями. Поэтому задача также была сведена к двумерной и решена в полярных цилиндрических координатах при принятых выше допущениях [4]. При одновременном воздействии силового поля (без учета касательных напряжений) и электромагнитного поля возбуждения состояние НМАС ЧЭ описывается дифференциальными уравнения- ми в полярных цилиндрических координатах. где γr и γφ – удельные электрические проводимости по направлениям; Er, Eφ, Hc – комплексы действующих значений напряженностей электрического и магнитного полей по поверхности сечения кольца по переменным r, φ и с; с = 2πr0 = const – длина кольца; μσ – магнитная проницаемость под действием механического напря- жения σ; wr – перемещение точки структуры по радиусу r; E – модуль упругости. Граничные условия при этом имеют вид (рис. 3) b ь Ис^ ФЛ*) = ffc(y) при — arcsin--- < ф < arcsin---. (21) V— — 2г в 2гв При малых углах φ имеем b ≈ L= . <^1 Нс(г, у) = 0 при ф = +arcsin —; Н ( ) = О при г = г о + -. Совместное решение уравнений тории ферромагнетизма (18) и упругости (19) в литературе позволяет при радиальном сжатии кольца определить магнитную проницаемость НМАС [1, 2]: 0,5632£a£g г0Р ° н н nB2abz где μн – начальная магнитная проницаемость; ∆μ – изменение магнитной проницаемости от P. Совместное решение системы уравнений электромагнитного поля (15-17) с условиями (2022) позволяет определить напряженности магнитного поля Hc и электрического поля Er и Eφ, параметры НМАС и далее преобразователя [1-7]. Рассмотренные физическая и математическая модели, как и предыдущие не отражают полную картину силового поля в ЧЭ, так как задача по существу решена в двухмерной плоскости. В реальных кольцевых ЧЭ имеет место сложная картина распределения механических напряжений, когда одновременно возникают различного вида напряжения сжатия σs, растяжения σp и сдвиговые (касательные) напряжения τ, которые не учитываются предыдущими моделями (рис. 3). Общее выражение для определения нормальных механических напряжений сжатия и растяжения в кольцевом ЧЭ под действием силы нажатия P записывается [1, 2, 5]: 0,5Р Г гл / гл \ 1 , (24) Ья L яка z J где верхние знаки относятся к наружной поверхности кольцевого ЧЭ, а нижние знаки – к внутренней поверхности ЧЭ. При θ=0 наружная поверхность ЧЭ сжимается под действием σc, а внутренняя растягивается под σр (см. рис. 3). При θ=π/2 картина меняется на обратную: наружная поверхность растяги- вается под σр, а внутренняя – сжимается под σc. Картина распределения напряжений повторяется для каждой четверти кольца. Используя обобщенную физическую модель ЧЭ на рис. 3, определяются максимальные напряжения сжатия σc при θ=0 и растяжения σр при θ=π/2 согласно выражений (24) и Учитывая 3-ю гипотезу прочности для ЧЭ и максимальные касательные напряжения определяются эквивалентные механические напряжения при работе ЧЭ на сжатие и растяжение [5-7]: стэс = V^Tb^-^CTp; Подстановка выражений (25) в формулы (26) и (23) позволяет получить: и определить магнитную проницаемость НМАС [1, 2]: , (28) где (-) – при сжатии элемента; (+) – при растя- жении элемента; μн – начальная магнитная проницаемость элементов 1 и 3 (рис. 1); ∆μ – изменение магнитной проницаемости. При принятых выше допущениях и предположениях при одновременном воздействии силового поля сжатия или растяжения и поля возбуждения состояние соответствующего неуправляемого ферромагнитного ЧЭ описывается дифференциальными уравнениями в сферических полярных координатах [5]: "9-с ЭЕ ЭЕ ЭВ -—!- — --- = —---= —jto^ Н ; dr Эср dt-т с ЭВ 1 ЭВ /эн эн эн' —+ —■ — ■— +—+ — ЭН^ В2 ЭН_ ^dffp Эас дт (dw dw dw=\ -+ —+- dr d где σэ – соответствующие эквивалентные напряжения кольцевых ЧЭ; γр и γφ – удельные электрические проводимости по направлениям; Er, Eφ, Hc – комплексы действующих значений напряженностей электрического и магнитного полей по поверхности сечения кольца по переменным r, φ и θ; с – длина кольца; r0 – средний радиус элемента; ω – круговая частота; μ σэ – магнитная проницаемость от механического напряжения σэ; wr, wφ и wθ – перемещение точек структуры по радиусу r, углам φ и θ; E – модуль упругости; θ – угол в радианах. Граничные условия при этом имеют вид (рис. 3): a Нс(г,ф) = Hc(r) приг = г0 + —; ф = О; т, < г< гн; (34) b ь Н^ ф,т) = H^q?) при — arcstn-- < ф < arcstn--; (35) — — 2гв 2г в При малых углах φ имеем b [' X Л I ° НАг, ф) = О при ф = -rarcstn —; п Е (36) v Нс^ ф,т) = 0 при г = г0 + с = j^ rQd6 =tq6, О < 6 < 2тг. (37) Уравнение ферромагнетизма (32) для НМАС решается исходя из энергетических соотношений ферромагнетика и результат его представлен в литературе [1, 2] в виде выражений (23) и (28). Уравнение теории упругости (33) рассмотрено с учетом 3-ей гипотезы прочности и его решение приведено в виде формул (26) и (27). Решение уравнений (29-33) с условиями (34- 37) позволили определить электрические и магнитные параметры объемной неуправляемой НМАС и далее всего МФУ [5, 6]. На рис. 3 представлена обобщённая физиче- ская модель управляемой НМАС. При принятых выше допущениях и предположениях при одновременном воздействии си- лового поля сжатия и электромагнитных полей возбуждения и управления состояние управляемого ферромагнитного ЧЭ1 описывается дифференциальными уравнениями в сферических полярных координатах [7]: где σэс – эквивалентные напряжения сжатия кольцевых ЧЭ; γр и γφ – удельные электрические проводимости по направлениям r и φ; Er, Eφ, Erу и Eφу – комплексы действующих значенrийφ наr-у пряженностей электрических полей от обмоток возбуждения и управления по направлениям r и φ; Bc, Hc, Bcy и Hcy – комплексы действующих значений магнитных индукций и напряженно- стей магнитного поля возбуждения и управления по направлению θ; ω – круговая частота; μ – магнитная проницаемость от эквивалентных механического напряжения сжатия; wr, wφ и wθ – перемещение точек структуры по радиусу r и углам φ и θ; r0 и с – средний радиус и длина кольцевого ЧЭ; μy – магнитная проницаемость от обмотки управления. Граничные условия при этом имеют вид (рис. 3): Н^г.ф) + Н^г.ф) = Н^г) + Яду (г), (43) а при Г = Гп = —: ф = О: Г, < Г < Г„; нХ<р,т) А-Н^ф/г) = Нс(ф) + Н^ф), (44) b b при — arcstn — < ф < arcstn —; 2гв 2гв При малых углах φ имеем b ≈ L= I Г0(1ф Для компенсационного ферромагнитного ЧЭ3 в уравнениях (38-42) и граничных условиях (43-45) поле управления равняется нулю (рис. 1). Уравнение ферромагнетизма (40) для напряженной магнитоанизатропной структуры НМАС управляемого ЧЭ1 и компенсационного ЧЭ3 (рис. 1) решено исходя из энергетических соотношений в литературе и выражение (28) принимает вид [1, 3, 7]: ^К ^у ^Н ^^ ”1" ^^у ^н "*~ ^^ ^^у ,(46) . 1,02Л„а5^гоР где Ди = ---, – изменение магнит- кБ^Ъа* ной проницаемости НМАС, созданное эквивалентным механическим напряжением сжатия σэс усилия Р; λs – изотропная магнитострикция материала элементов; αs – коэффициент намагниченности материала; μн – начальная магнитная проницаемость элементов 1 и 3; r0 – средний радиус элемента; a и b – толщина и ширина элемента; μу и μк – магнитные проницаемости управляемого 1 и компенсационного 3 элементов (рис. 1). Уравнение теории упругости (42) рассмотрено с учетом 3-ей гипотезы прочности и его решение представлено в виде формул (25) и (27). Решение уравнений (38-40) с условиями (4345) электромагнитного поля с учетом уравнений ферромагнетизма (41) и теории упругости (42) позволили рассчитать электрические и маг- нитные параметры НМАС и всего МФУ, которые представлены в литературе [7]. Рассмотренные модели НМАС были реализованы на опытных образцах МФУ и широко представлены в литературе [1-7], что позволило дать экспериментальную оценку этим моделям. Анализ моделей НМАС показал, что все они могут использоваться для расчета МФУ. Однако, наиболее сложной для практического применения является трехмерная модель НМАС в виде ферромагнитной пластины в декартовых координатах, так как она не полно отображает физические процессы в ней. Погрешность таких моделей НМАС достаточно велика и составляет до 25% [1, 2]. Модели НМАС в виде ферромагнитного кольца в полярных цилиндрических координатах в трехмерном пространстве полнее и точнее отображают физические процессы в ЧЭ, но анализ по существу сводится к двухмерной модели. Погрешность таких моделей при практической реализации может достигать до 15% [4]. Наиболее полную реальную картину физических явлений в НМАС отображают физическая и математическая модели НМАС в трехмерном пространстве в виде ферромагнитной кольцевой структуры в электромагнитном поле при силовом воздействии в полярных сферических координатах. Точность таких моделей гораздо выше и составляет до 10% [5]. 2. 3. 4. 5. 6. 7.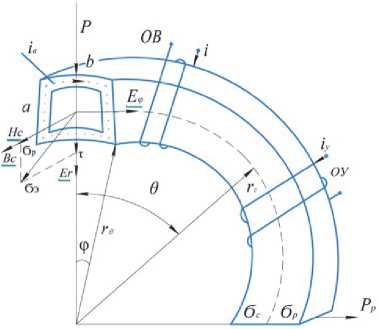
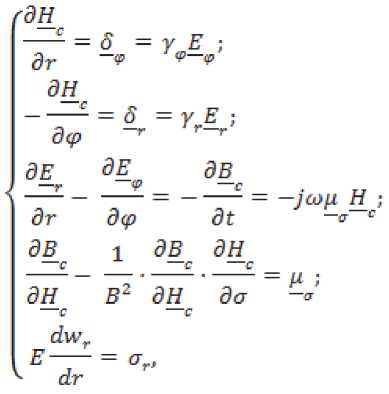
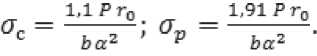
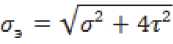
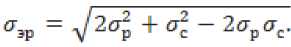
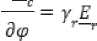
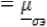
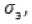
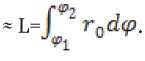
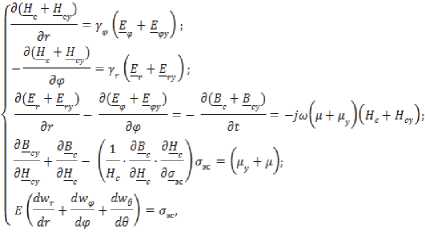
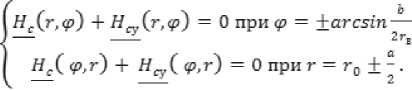
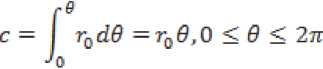
Список литературы Анализ физических и математических моделей напряженных магнитоанизотропных структур
- Дубинин А.Е. Магнитоанизатропные устройства автоматизированных систем / А.Е. Дубинин, А.Л. Кислицын. Ульяновск: УлГТУ, 2004. - 372с.
- Дубинин А.Е. Магнитоанизатропные преобразователи силы. М.: Энергоатомиздат, 1991. - 112 с.
- Дубинин А.Е., Капитуров Р.Е., Дубинин А.А. Исследование магнитоанизатропных ключевых элементов для системы контроля тягового электродвигателя // Известия Самарского научного центра Российской академии наук. 2010. Т. 12.№ 4. - С. 51-58.
- Дубинин А.Е., Зорина А.В., Дубинин А.А. Математическая модель устройств на базе напряженных магнитоанизатропных структур // Известия Самарского научного центра Российской академии наук. 2013. Т. 15. № 4. - С. 65-70.
- Дубинин А.Е., Дубинин А.А. Математическая модель напряженных магнитоанизатропных структур устройства телеметрического контроля тягового электродвигателя // Вестник транспорта Поволжья. - Самара: СамГУПС. 2013. № 1 (37). С. 34-43.
- Дубинин А.Е., Дубинин А.А., Цаплин Н.Н. Математическая модель напряженной магнитоанизатропной структуры устройства телеметрии силового воздействия // Известия Самарского научного центра Российской академии наук. 2016.Т.18. № 4. - С. 139-142.
- Дубинин А.Е., Пугачев Я.Н., Ахмадуллин Ф.Р. Математическая модель магнитоанизатропных ключевых элементов // Вестник транспорта Поволжья. - Самара: СамГУПС. 2019. № 2(74). С. 60-68.


