Анализ формирования дислокационных структур монокристалла

Structure changes of monocrystals represents the fundamental phenomenon and is observed in crystals with various type of a lattice at the most different schemes and modes of plastic deformation. After introduction by Taylor, Orovan and Poljani in 1934 of concept of a disposition, the defective crystal structures in the majority of works is understood as a spatial arrangement of dispositions. Dislocation structures type of a material defines its mechanical characteristics. Therefore the works devoted to studying processes of evolution dislocation structures of crystals are perspective. This paper presents an attempt of evaluation defective structure processes investigation.

Изменение структуры монокристаллов представляет собой фундаментальное явление и наблюдается в кристаллах с различным типом решетки при самых разных схемах и режимах пластической деформации. После введения Тейлором, Орованом и Поляньи в 1934 году понятия дислокации под дефектной структурой кристаллов в большинстве работ понимается пространственное расположение дислокаций, именно тип дислокационной структуры материала, определение его механических макроскопических характеристик. Поэтому перспективными являются работы, посвященные изучению процессов эволюции дислокационного строения кристаллов. В данной работе предпринята попытка исследования процессов изменения дефектной структуры материала с помощью модели дислокационной динамики.

Наблюдение дислокаций в экспериментах

На сегодняшний день наиболее распространенным методом изучения дислокационных структур, полученных в ходе эксперимента, все еще остается визуальное изучение изображений, полученных с помощью электронной микроскопии. Данный метод применяется для тонких, специально изготовленных срезов металла. Волны, проходя через тонкую металлическую фольгу, частично дифрагируют на кристаллической решетке, отражаясь от ее атомных плоскостей по закону Вульфа - Брэгга и отклоняясь при этом от направления первичного пучка. Интенсивность пучка лучей, прошедших через фольгу и узкую диафрагму, отсекающую отклонившиеся лучи, равна разнице интенсивности первичного и дифрагированных лучей. При этом дислокации проявляются в виде темных линий (рис. 1).

После получения изображения можно определить дислокационную структуру, а также рассчитать основные параметры дислокационного строения материала. К сожалению, данный подход весьма трудоемок и не позволяет изучать объемные дислокационные субструктуры.

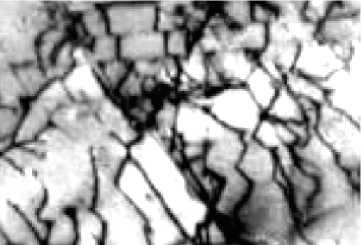
Тем не менее на сегодняшний момент электронная микроскопия яв ляется единственным методом, позво-

Рис. 1. Изображение дислокаций [1] ляющим определять тип дефектной структуры материала [2].

Классификация дислокационных структур [1-4]

Общепризнанным на сегодняшний день является разделение дислокационных структур на низкоэнергетические и высокоэнергетические; соответственно, классификационным признаком является энергия этих структур. Поскольку на практике в процессах холодной обработки материалов давлением низкоэнергетические структуры встречаются гораздо чаще, в дальнейшем речь пойдет именно о них. Основной особенностью всех низкоэнергетических структур является то, что дислокации в этих структурах стремятся занять такое пространственное положение, при котором энергия поля упругих напряжений была бы минимальна.

Вторым общепринятым критерием для дислокационных структур является наличие или отсутствие взаимной разориентировки отдельных подобластей материала друг относительно друга. Появление разориентированных структур в материале свидетельствует о начале фрагментации.

Неразориентированные структуры

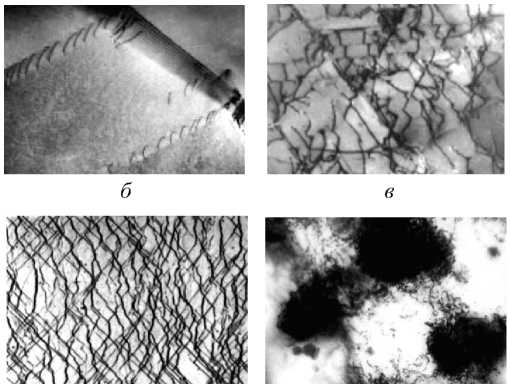
В этом классе выделяют: 1) хаотическое распределение дислокаций (хаос), 2) скопления дислокаций, 3) дислокационные сетки, 4) дислокационные клубки, 5) ячейки, 6) ячеисто-сетчатую структуру (рис. 2).

Следует заметить, что вне зависимости от степени деформации в материале всегда существуют области с повышенной и пониженной плотностью дислокаций. Конкретные типы дислокационных структур определяются по расположению дислокаций в областях с повышенной плотностью. Например, на рис. 3 изображены дислокационные «вены», образованные

a

г

д

е

Рис. 2 Примеры низкоэнергетических дислокационных структур: a - хаотическое распределение; б - дислокационные скопления; в , д - сетчатая структура; г - нера-зориентированные ячейки; е - клубковая структура) [4]

Рис. 3. Дислокационные «вены» (viens) [1]

дислокационными сетками. При этом нельзя исключать ситуации, при которых разные области соответствуют разным типам субструктур.

Такие структуры, как хаос или скопления, соответствуют начальным этапам пластической деформации, при этом в областях с повышенной плотностью дислокации распределены случайным образом. При дальнейшей пластической деформации происходит образование дислокационных сеток и клубков. В отличие от хаотического скопления эти структуры обладают регулярным расположением дислокаций.

Дальнейшее увеличение пластических деформаций приводит к образованию структур, обладающих дислокационными границами (ячейки, ячеисто-сетчатые структуры).

Разориентированные структуры

К разориентированным структурам относятся следующие (рис. 4): 1) ячейки с разориентировками, 2) ячеисто-сетчатая с разориентировками, 3) микрополосовая, 4) субструктуры с многомерными дискретными и плавными разориентировками, 5) фрагментированная, 6) двойниковая.

1                    2

Рис. 4. Разориентированные дислокационные структуры: 1 - ячеистая; 2 - ячеистосетчатая; 3 - полосовая; 4 - фрагментированная [4]

Эволюция дислокационных структур

Согласно экспериментальным данным переход от одного типа дислокационной структуры к другому отчетливо коррелирует со стадиями пластической деформации и является неслучайным (рис. 5).

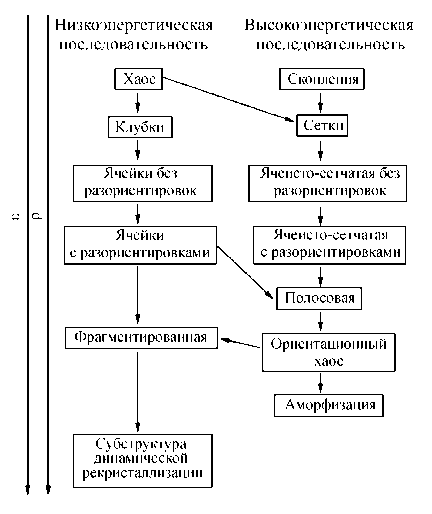
Рис. 5. Последовательность появления различных типов дислокационных структур [2]

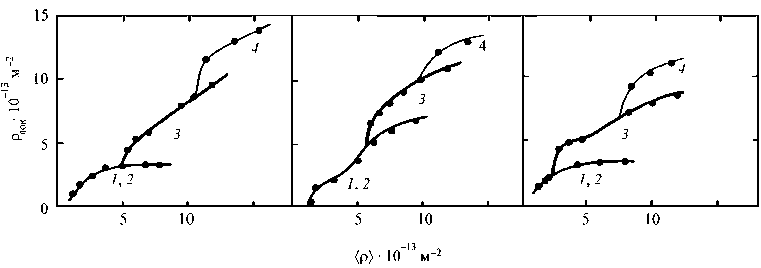
Любопытным является тот факт, что каждая субструктура появляется только по достижении определенного критического значения плотности дислокации. Величина этого критического значения плотности дислокаций может отличаться для разных материалов, но не слишком значительно. Смена типа дефектной структуры происходит плавно: по достижении плотности дислокаций определенного значения начинает возрастать доля дислокаций, располагающихся в соответствии с новой дефектной структурой, в то время как доля дислокаций в существующих уже структурах перестает расти и может даже начать уменьшаться (рис. 6).

а

б

в

Рис. 6. Зависимости плотностей дислокаций от средней плотности по материалу в сплавах на основе меди: а - Cu + 5 ат. % Al, б - Cu + 0,5 ат. % Al, в - Cu + 0,4 ат. % Mn [2]; 1 - дислокационный хаос, 2 - дислокационные скопления, 3 - ячейки без разворотов, 4 - ячейки с разворотами

Дислокационная динамика [5-11]

Ввиду технической сложности экспериментального изучения процессов эволюции дислокационных структур в последние годы широко применяется расчет поведения дислокаций на ЭВМ. Такой подход получил названия дислокационной динамики .

На сегодняшний день наибольшее распространение получил так называемый «параметрический» подход дислокационной динамики. Суть этого подхода состоит в представлении дислокации с помощью узлов, соединенных сегментами дислокации (рис. 7).

В общем случае один узел может иметь произвольное количество соседних узлов, обозначим через b j вектор Бюргерса, соответствующий сегменту дислокации, соединяющего г -й узел с j- м.

Узел, имеющий только двух соседей, будем называть аппромаксион-ным. Узел, имеющий больше двух соседних узлов, является точкой ветвления дислокации, такие узлы называются физическими. Следует заметить, что линия одной дислокации представляется набором аппромаксионных узлов, соединенных между собой сегментами. При этом из кристаллографии следует, что вектор b j остается постоянным для любого сегмента линии дислокации.

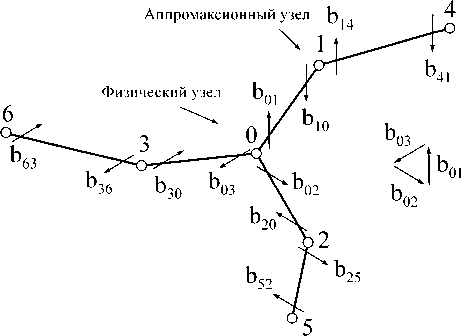
Рис. 7. Аппроксимация дислокации с помощью узлов [7]

Важным аспектом моделей дислокационной динамики является способ определения силы, действующей на узел. Рассмотрим общий алгоритм определения этой силы. Сила, действующая на узел, может быть определена через градиент упругой энергии [7-11]:

F = д£( j

*         ^д Г _;

где £ ( r ) - упругая энергия, определяющаяся положением всех узлов в системе. Упругую энергию удобно разделить на два слагаемых - энергию ядра дислокации и энергию взаимодействия сегментов дислокаций,

£ = £ c + £ el .

Соответственно сила, действующая на Z- й узел, также может быть расписана в виде суммы:

F = F c + F el .

Каждая из составляющих силы, действующих на выбранный узел, определяется через рассмотрение сил, связанных с сегментами дислокаций этого узла.

Рассмотрим энергию ядер сегментов узла, для этого воспользуемся следующим соотношением [7]:

n - 1   n

у X

£c = XX ec bzj

,

z = 1 j = z + 1

V

ЙI1 N^

где е - линейная энергия сегмента ij, lj = rj - ri - радиус вектор, проведенный из i-го в j-й узел. Тогда dec дГ

^F i^c

= P f C ,

,

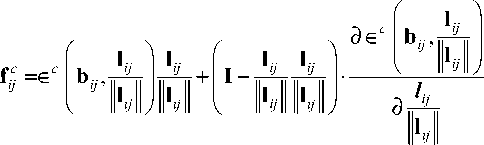
где f c - сила ядра сегмента дислокации ij. Первый член выражения для f j соответствует линейному натяжению дислокации и стремится уменьшить длину сегмента ij. Второй член этого выражения отражает силу, стремящуюся развернуть данный сегмент в положение с наименьшей энергией.

Вторая составляющая силы, обусловленная взаимодействием дислокаций с различными дальнодействующими полями других дислокаций, внешним напряжением и так далее, тоже раскладывается на составляющие:

F l = £ f j^l , (6)

где f j! - сила, действующая на сегмент, соединяющий i- й узел c j- м. Обычно ограничиваются рассмотрением влияния следующих составляющих этой силы: внешнего приложенного напряжения , силы линейного натяжения и силы взаимодействия с другими сегментами:

n-1 n fij = f+ fis + PP fk, [ k, l ] * [ i, j ] и [ j, i ], (7) k=11=k+i где f ext - внешняя сила, действующая на сегмент ij; fi - сила линейного натяжения сегмента ij; fк - сила, обусловленная взаимодействием сегмента ij с сегментом kl.

Для определения скорости узла используется так называемая функция мобильности (mobility function) , связывающая скорость узла с силой, действующей на этот узел [7, 8, 9]:

v(x) = M(f(x)) , (8)

где v - скорость линии дислокации в точке x ; f - сила, действующая на дислокацию в точке х ; М - некоторый оператор, определяющий связь силы, действующей на дислокацию в точке х , и скорость дислокации в этой же точке.

Вообще говоря, эта функция «содержит» в себе информацию о материале. На практике чаще всего используют следующую функцию мобильности [8]:

v(x) = B(b,t) х f(x) ,,                             (9)

где B - тензор «переноса», b - вектор Бюргерса дислокации, t - единичный вектор вдоль линии дислокации.

Рассмотрим пример построения этого тензора. Как известно, чисто винтовые дислокации могут перемещаться в любом направлении, перпендикулярном линии дислокации. Тогда направление скорости дислокации может быть определено как проекция силы, действующей на дислокацию, на плоскость, перпендикулярную линии дислокации,

B(b,t) = B s (I - tt) ,                             (10)

где B s - некоторый коэффициент, численно равный скорости дислокации при воздействии на нее единичной силой.

Далее рассмотрим чисто краевую дислокацию. Известно, это такая дислокация может двигаться только в плоскости своего скольжения или переползать перпендикулярно ей. Исходя из этого, тензор переноса можно записать следующим образом:

B(b,t) = Begbb + Bec nn, b х t                                         (11)

n = 1 b х Ц.

Для случая смешанной дислокации можно использовать комбинацию (10) и (11):

B(b,t) = B_g bb + B c nn,

_- 1

B g =1 M [ B ^-2| > х t|| ²+ B - (b • t) ² ]"²,                   (12)

B c = H [ B g b ^х ' ' ^{B (b} • ^{,) !} ]

Значения коэффициентов B eg , B_c и B s обычно подбираются опытным путем.

Существующие модели дислокационной динамики применяются только для монокристаллических материалов. В силу этого они по определению не позволяют моделировать поведение разориентированных дислокационных структур. С другой стороны, чтобы учитывать в моделях процессы разворота одной области кристалла относительно другой, необходимо иметь возможность определения текущей дислокационной структуры.

Анализ дислокационных структур

Для получения распределений дислокаций в моделируемом объеме использовалась модель дислокационной динамики. При этом моделировалось поведение полных закрепленных (источник Франка - Рида) и свободных дислокаций объемно-центрированного кристалла. С помощью дислокационной динамики можно получить трехмерную дефектную структуру материала и построить трехмерное изображение этой структуры (рис. 8), однако при этом остро встает вопрос о способах обработки полученных результатов. К сожалению, визуальное наблюдение трехмерного распределения дислокаций по объему не позволяет определить необходимые характеристики структуры материала (см. рис. 8). В связи с этим актуальной задачей является разработка методов, позволяющих определять характер дислокационной структуры путем автоматической обработки результатов расчетов.

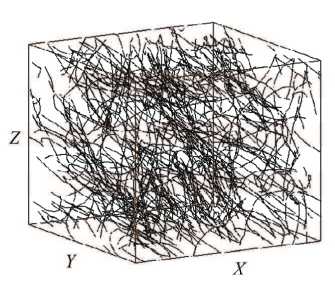
Рис. 8. Пример трехмерного распределения дислокаций по объему, полученных в ходе численных экспериментов

В данной работе для исследования эволюции дислокационной структуры был разработан механизм сканирования моделируемого объема «прозрачной» ячейкой определенного фиксированного размера, при перемещении которого с заданным шагом по кристаллу с дислокациями рассчитывается плотность дислокаций, попавших в ячейку. Эта плотность относилась к центру ячейки. Таким образом, после сканирования всего моделируемого объема мы получали функцию распределения плотности дислокаций от координат. В ходе такого сканирования легко определяются области с повышенной плотностью дислокаций (то есть области дислокационных скоплений).

Описанный выше метод был применен для анализа эволюции дислока- ционных структур, полученных в ходе численного эксперимента на одноосное растяжение титана. Направление оси приложенного нагружения по отношению к кристаллографической системе координат (КСК): [111], скорость нагружения 1 МПа/с, размер ребра куба (моделируемой области) 2,64Т0-6 (м).

В ходе статистического анализа распределения плотности дислокаций были получены зависимости изменения средней плотности дислокаций в сканирующей ячейке от пластических деформаций (рис. 9). Как и следовало ожидать, по мере увеличения пластических деформаций происходит интенсивная работа источников Франка-Рида, а также увеличивается интенсив- ность дислокационных реакций, что приводит к общему росту скалярной плотности дислокаций в моделируемом объеме (рис. 10), равно как к увеличению и средней плотности в сканирующей ячейке.

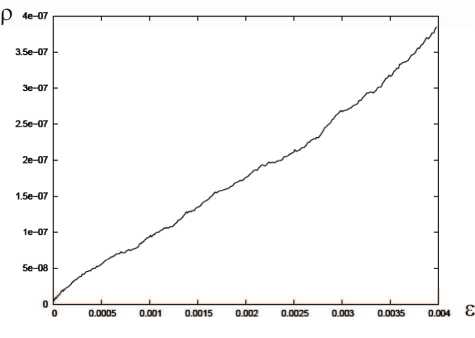
Рис. 9. Зависимость средней плотности дислокаций в ячейке

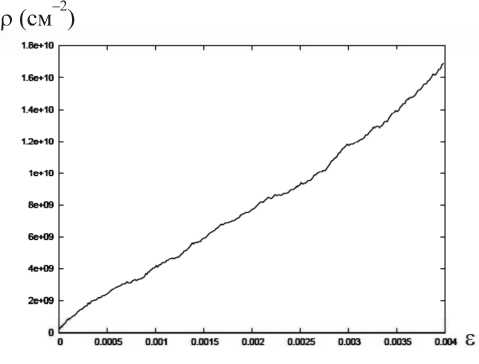
Рис. 10. Зависимость плотности дислокаций

Кроме того, в рамках статистического анализа также фиксировалась дисперсия плотности дислокаций в сканирующей ячейке (рис. 11). Из полученных зависимостей следует, что по мере увеличения пластических деформаций растет разброс плотности дислокаций в сканирующей ячейке. Это означает, что в моделируемом объеме образуются области с повышенной дислокационной плотностью.

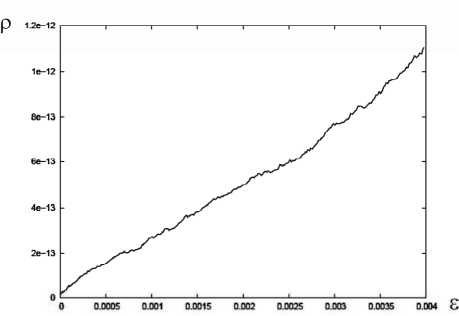
Рис. 11. Зависимость дисперсии плотности дислокаций в ячейке

Кроме того, после получения трехмерного распределения плотности дислокаций было осуществлено сканирование этого распределения с помощью секущих плоскостей. На рис. 12 приведены изображения, полученные для среза x = 0 с помощью плоскостей с различной толщиной. Исследования показали, что для наблюдения дислокационных структур при достаточно развитых пластических деформациях (а точнее, при достаточно высокой плотности дислокаций) достаточно небольшой толщины секущей плоскости. Более того, если толщина секущей плоскости будет слишком большой, из-за большой плотности дислокаций на полученном рисунке можно будет увидеть только «белый шум», а не дислокационные структуры. Поэтому для дальнейшего анализа толщина секущей плоскости была принята равной 0,00026 м.

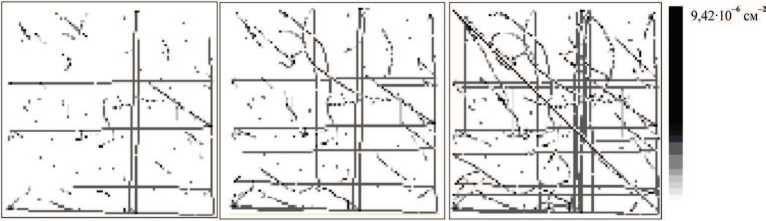
а                     б                    в

Рис. 12. Срезы различной толщины: a - 0,00026 м, б - 0,00066 м, в - 0,00132 м

Далее был осуществлен анализ изображений, полученных при помощи секущей плоскости выбранной толщины. Полученные изображения свидетельствуют о том, что до 0,001 м (рис. 13-16) никакой дислокационной структуры как таковой не образуется, а в секущую плоскость попадают две-три дислокации, параллельные ей, а также несколько пересекающих их

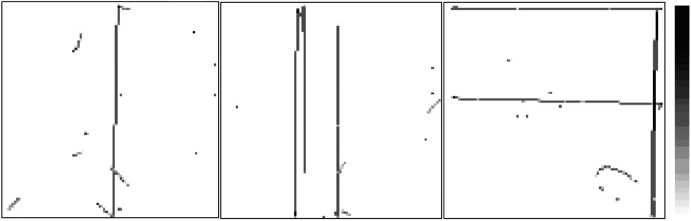
а                     б                      в

Рис. 13. Срезы при е = 0,00003 м: a - x = 0; б - у = 0; в - z = 0

а                      б                     в

Рис. 14. Срезы при е = 0,0001 м: a - x = 0; б - у = 0; в - z = 0

а                     б                      в

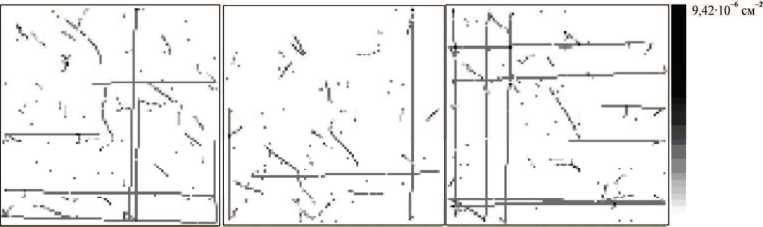
Рис. 15. Срезы при е = 0,0005 м: a - x = 0; б - у = 0; в - z = 0

а                     б                     в

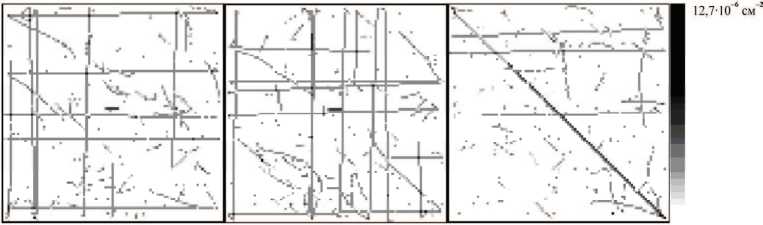
Рис. 16. Срезы при е = 0,001 м: a - x = 0; б - у = 0; в - z = 0

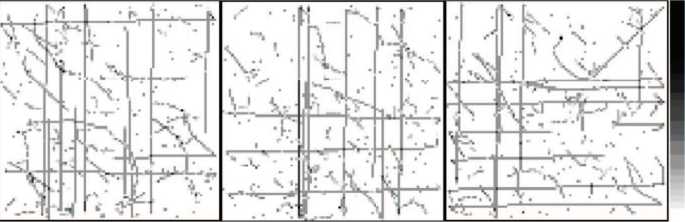
под углом. По мере увеличения деформации количество дислокаций, попадающих в секущие плоскости, растет. Примерно с 0,002 м (рис. 17) начинает отчетливо проявляться дислокационная сеть. При достижении 0,004 м (рис. 19) дислокационная сетка становиться очень плотной.

а                      б                     в

Рис. 17. Срезы при е = 0,002 м: a - x = 0; б - у = 0; в - z = 0

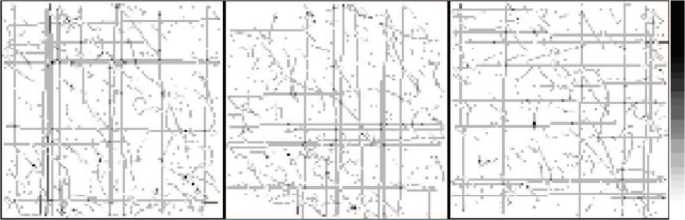
а                     б                     в

Рис. 18. Срезы при е = 0,003 м: a - x = 0; б - у = 0; в - z = 0

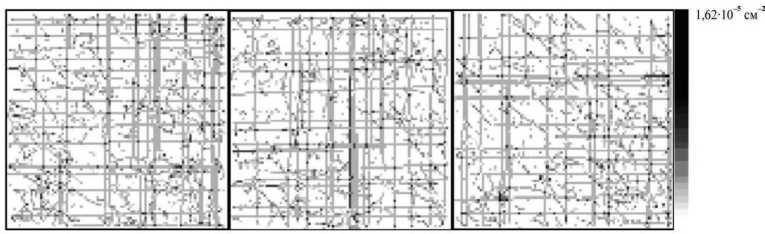
a

б

в

Рис. 19. Срезы при е = 0,003 м: a - x = 0; б - у = 0; в - z = 0

В заключение следует заметить, что анализ проводился при сравнительно небольших пластических деформациях, что связано с большими вычислительными затратами. Ввиду этого образовавшиеся дислокационные структуры не успели четко сформироваться. Кроме того, при исследовании выделенных дислокационных скоплений необходимо проводить морфологический анализ, например, исследовать размеры подобластей в скоплении с заданной плотностью дислокаций.

Работа выполнена при финансовой поддержке РФФИ (гранты 10-08-00156-а, 10-08-96010-р_урал_а).