Анализ формы и темпа продвижения твердой фазы при направленной кристаллизации цветных металлов с электромагнитным воздействием ультразвуковым и температурным методами

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2022PNRPU MECHANICS BULLETIN

Процессы кристаллизации расплавов металлов и полупроводников характеризуются комплексом разнообразных физических явлений, в совокупности определяющих структурные особенности и механико-прочностные характеристики изделий. Одним из важнейших факторов, влияющих на структуру кристаллической фазы, являются течения, возникающие в жидкой фазе слитка в процессе затвердевания [1]. Топология таких течений, очевидно, должна влиять на процессы, протекающие при его кристаллизации. Например, в случае цилиндрической геометрии азимутальное перемешивание расплава приводит к однородному распределению вводимых добавок, а также ломке дендритов на фронте кристаллизации расплава. Возбуждение меридиональных течений улучшает перемешивание вводимых компонентов и влияет на форму границы «расплав – твердая фаза» [2–6].

В отсутствие внешнего принудительного перемешивания основным источником течений, влияющих на тепломассоперенос, является свободная тепловая конвекция, возникающая под действием перепада температур между жидкой и твердой фазами [7; 8]. Во многих случаях влияние конвективных течений оказывается негативным, поскольку неконтролируемым образом изменяет условия теплообмена в области кристаллиза- ции расплава [9–11]. В то же время конвективные течения оказываются недостаточно интенсивными для желательного перемешивания при отливке изделий из металлов.

Для подавления паразитных конвективных течений и (или) усиления желательных используется принудительное перемешивание. В силу электропроводности расплавов металлов и полупроводников возможен бесконтактный электромагнитный метод генерации течений в жидкой фазе. Под воздействием внешнего переменного электромагнитного поля в проводящей среде возникают вихревые токи. Взаимодействие этих токов с исходным полем приводит к возникновению объёмной силы. Если проводящая среда является текучей, то данная сила порождает вихревые течения жидкости, топология которых определяется топологией электромагнитного воздействия [12–17].

Широкое распространение в металлургии получило применение бегущего (БМП) и вращающегося (ВМП) магнитных полей. Суть обоих методов сводится к генерации интегральной средней силы, толкающей расплав за счёт последовательного изменения фазы переменных магнитных полей разнесенных в пространстве катушек (как правило связанных общим магнитопроводом). Управление топологией и интенсивностью генерируемых течений осуществляется путём вариации амплитуды и частоты питающих индуктор токов.

Мы предлагаем новый способ опосредованного управления процессом кристаллизации металлического расплава посредством изменения фазных углов токов питания линейного индукционного перемешивателя. Изменение распределения фаз переменных магнитных полей отдельных катушек вдоль индуктора изменяет топологию электромагнитных сил в рабочей жидкости и открывает широкие возможности для управления структурой течений [18].

Высокие температуры плавления и химическая активность подавляющего числа металлических расплавов в значительной мере ограничивают спектр экспериментальных методик, доступных для изучения МГД-процессов. Мы моделируем процессы перемешивания на легкоплавком галлиевом сплаве. Данный сплав обладает рядом преимуществ, делающих его идеальной средой для изучения МГД-процессов в лабораторных условиях. Сплавы на основе галлия сохраняют текучесть при комнатных температурах, нетоксичны (в отличие от ртути), химически малоактивны (в сравнении, например, с NaK), негорючи [19].

Одним из мощных методов измерений характеристик гидродинамических процессов, применимых в оптически непрозрачных средах, является ультразвуковая допплеровская анемометрия [20–23]. Этот метод позволяет измерять пространственные профили компоненты скорости, направленной вдоль ультразвукового луча, а также профили ультразвукового эха, связанные с фазовым составом среды. Тем не менее ультразвуковые измерения становятся невозможны в расплавах, применяемых в промышленности металлов, в силу высокой чувствительности пьезоэлементов ультразвуковых преобразователей к повышенным температурам. Ограниченный диапазон рабочих температур датчиков требует разработки новых методов измерений, применимых для анализа таких комплексных процессов, как управление направленной кристаллизацией, в реальных промышленных металлах (например, Al, Mg, Ti и др.). Ультразвуковой метод является прямым и потому может быть использован для верификации косвенных измерений [24; 25].

Удобный инструментарий для анализа темпа и однородности кристаллизации предоставляют локальные измерения температуры при помощи плотной сетки термопар. Термопары во многом лишены ограничений пьезоэлементов и могут быть использованы в дальнейшем для изучения процессов в средах, нагретых до высоких температур. Поэтому целью данной работы является разработка и апробация методики измерения темпа и формы фронта кристаллизации в процессе затвердевания металлического расплава, находящегося под внешним электромагнитным воздействием.

1.    Методология

Экспериментальная установка (рис. 1) представляет собой плоский вертикальный слой жидкого металла, размещенный над индуктором линейной индукционной машины (ЛИМ) 1. Жидкий металл заключен в кю- вету 2 из стеклотекстолита. С торцевых сторон слоя размещаются медные теплообменники 3, подключенные через систему вентилей к криотермостатам КРИО ВТ-1. Кювета оборудована вставной стенкой 4, в которой размещен набор малоинерционных термопар. Измерения скорости течения жидкого металла производятся при помощи пяти датчиков TR0408LS ультразвукового допплеровского анемометра (УДА) DOP 2000, Signal Processing, Switzerland [26]. Датчики располагаются в пазах медной стенки 5 таким образом, что ультразвуковые лучи направлены вдоль слоя по оси X. С внешней стороны кювета теплоизолирована слоем стекловаты. Размеры рабочей полости кюветы 420x20x100 мм3. Планарные размеры ЛИМ 480x350 мм2. Магнитное поле генерируется шестью катушками по 170 витков в каждой. Питание ЛИМ осуществляется от трёхфазного программируемого источника Pacific Smart Source 360 ASX-UPC3 3, позволяющего задавать напряжения и фазные углы каждой из фаз, контролировать силу и частоту тока. Несущая частота магнитного поля составляла 50 Гц.

Теплообменники создают в слое жидкого металла горизонтальный градиент температуры вдоль оси X . Торцевая поверхность теплообменников, находящаяся в контакте с жидким металлом, облужена галлием для обеспечения наилучшего теплового контакта между жидкостью и теплообменниками. Температура горячего теплообменника составляет +18°C, температура холодного составляет –30°C.

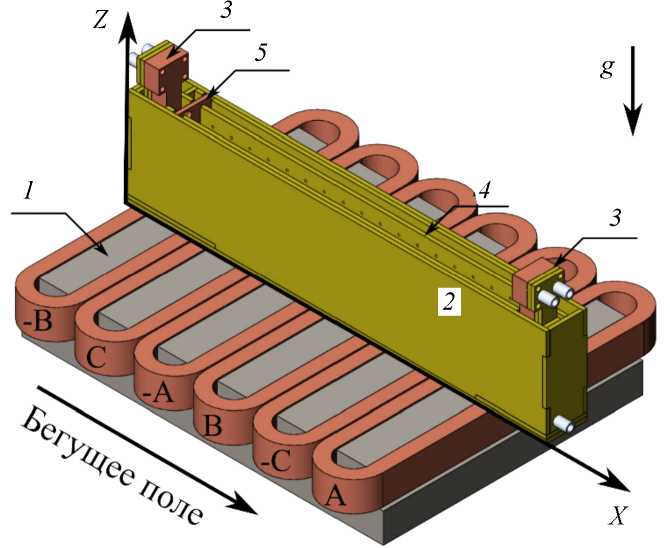
Рис. 1. Схема экспериментальной установки: 1 – ЛИМ; 2 – ячейка из стеклотекстолита; 3 – теплообменники; 4 – вставная стенка; 5 – медная стенка. Направление БМП указано длинной черной стрелкой вблизи индуктора, направление силы тяжести отмечено короткой стрелкой g . Заглавными буквами на катушках отмечены фазы токов питания

Fig. 1. Sketch of the experimental setup: 1 – LIM; 2 – fiberglass cell; 3 – heat exchangers; 4 – false wall; 5 – copper wall. The direction of the TMF is indicated by a long black arrow near the inductor, the direction of gravity is indicated by a short arrow g . The capital letters on the coils indicate the phases of the supply currents

В качестве рабочей жидкости используется сплав Ga 86.3 Zn 10.8 Sn 2.9 (вес. %). Физические свойства сплава при комнатной температуре: плотность 6256 кг/м³, коэффициент объёмного теплового расширения 9,63·10^–5 1/K, кинематическая вязкость 3·10^–7 м²/с, проводимость 3,56·10⁶ См/м, скорость звука в среде 2870 м/с, температура плавления сплава +17 °C. Более подробно свойства сплава см. в [19; 27].

Измерения скорости проводятся при помощи УДА. Принцип действия прибора основывается на излучении ультразвуковых волновых пакетов в жидкую среду, последующим их отражением от движущихся вместе со средой частиц и приёме отраженного эхо. Сдвиг частот между излученным и принятым волновыми пакетами пропорционален скорости движения звукоотражающих частиц в соответствии с эффектом Допплера. Наличие таких частиц в жидкости является обязательным требованием для данного метода, размеры не должны превышать длину ультразвуковой волны. При этом концентрация частиц должна быть достаточно малой, чтобы превалирующим механизмом процесса было отражение, а не рассеяние ультразвуковых волн. В сплавах на основе галлия такими частицами служат оксиды галлия. Контакта сплава с атмосферой в течение одной минуты оказывается достаточно для достижения необходимой концентрации оксидных частиц. Характерные размеры частиц – от единиц до десятков микрон, длина звуковых волн порядка 700 мкм.

Локализация положения фронта кристаллизации производится при помощи УДА. На границе раздела фаз (например «жидкость – твердое тело») происходит скачок акустического сопротивления (произведения плотности среды на скорость звука). При прохождении через границу раздела фаз происходят множественные переотражения волновых пакетов, что выражается в виде локального максимума на пространственном профиле эхо. Положение этого локального максимума соответствует положению границы раздела фаз, в данном случае положению фронта кристаллизации [28–30]. Анализ профилей ультразвукового эхо позволяет восстановить положение и форму фронта кристаллизации в каждый момент времени по данным 5 датчиков УДА.

На рис. 3 приведён пример пространственных профилей продольной компоненты скорости течения и ультразвукового эха в заданный момент времени. Красными вертикальными линиями отмечены границы области фазового перехода. В этой области происходит увеличение интенсивности ультразвукового эха в силу множественных переотражений. Продольная компонента скорости обращается в ноль в выделенной области в силу поворота потока на твёрдой границе раздела фаз. Синей вертикальной линией на рисунке отмечено положение границы раздела фаз, найденное с использованием алгоритма поиска локальных максимумов. Локальный максимум на профиле эха в области x ≈ 400 мм обусловлен наличием медного теплообменника и пере-отражениями ультразвука на границе «твёрдый галлие- вый сплав – медная стенка». При этом профиль скорости в области за границей раздела фаз (правее синей линии на рисунке) не имеет физического смысла, и рассчитывается УДА на основе вторичных отражений ультразвука.

Вторым методом контроля процессов, происходящих в слое металла, является анализ данных температурных датчиков. Во вставной стенке кюветы расположены два набора малоинерционных термопар с диаметром термоспая ≈ 0,5 мм, как показано на рис. 2. Термопары, расположенные по длине кюветы, служат для определения скорости продвижения фронта кристаллизации в разные моменты времени, в то время как ряд термопар, расположенных по высоте слоя, позволяет определить его форму.

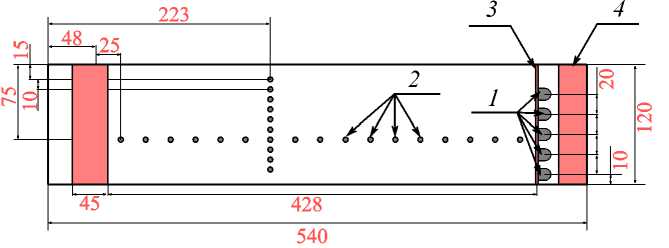
Рис. 2. Схема расположения ультразвуковых и термопарных датчиков в слое: 1 – датчики УДА; 2 – термопары; 3 – медная стенка; 4 – теплообменник. Цветные подписи отображают пространственные размеры установки (мм)

Fig. 2. Sketch of ultrasonic and thermocouple sensors in the layer: 1 – UDV sensors; 2 – thermocouples; 3 – copper wall; 4 – heat exchanger. Color labels display the spatial dimensions of the setup (mm)

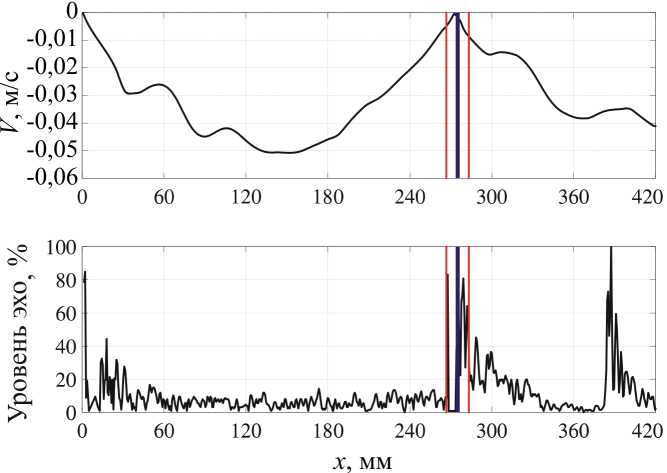
Рис. 3. Пространственные профили скорости течения (сверху) и ультразвукового эха (снизу) в конкретный момент времени, полученные при помощи УДА. Красные линии отмечают границу области фазового перехода, синей линией отмечено положение фронта кристаллизации, определенное в ходе анализа профиля эхо

Fig. 3. Spatial profiles of velocity (top) and ultrasonic echo (bottom) at a specific moment of time, obtained using UDV. The red lines mark the boundary of the phase transition region, the blue line marks the position of the crystallization front, determined during the analysis of the echo profile

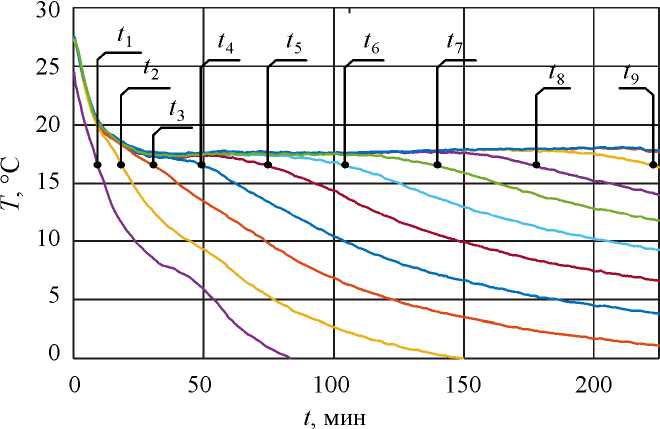
Рис. 4. Эволюции температуры жидкого металла на термопарах вдоль кюветы с указанием моментов времени кристаллизации

Fig. 4. Evolution of the liquid metal temperature on a thermocouple along the sell with indication of crystallization time points

Для получения данных о скорости движения фронта кристаллизации вдоль слоя жидкого металла достаточно знать расстояние d между термопарами и определять моменты времени t i , в которые происходит кристаллизация объёма вблизи i -й термопары. Как видно из рис. 4, большинство кривых эволюций температуры имеют сходный вид: быстрое снижение от температуры окружающей среды до температуры солидуса, участок плато и плавное снижение, свидетельствующее об окончании процесса кристаллизации в объёме вблизи термопары. Момент кристаллизации может быть найден по отклонению от нуля производной по времени температурного ряда (взятого с начала плато), но на первых трёх термопарах такого плато не наблюдается во всех рассмотренных режимах вследствие быстрого продвижения фронта в начале процесса кристаллизации. Возможно применение иного метода, при котором используется пороговая температура ниже точки кристаллизации. Достижение этой температуры считается достаточным условием для гарантированной кристаллизации металла. Второй метод, очевидно, применим для всех кривых на рис. 4, вне зависимости от наличия участка плато. Второй метод позволяет более точно оценить скорость кристаллизации за счёт снижения точности определения положения фронта кристаллизации. Мы использовали данный метод, установив значение пороговой температуры равным 16,5 °C. Скорость движения фронта кристаллизации в моменты времени ( t_i + t_{i + 1} ) /2, i = 1..8 рассчитывалась по формуле (1):

U i =

координаты x_k , k = 1…8 положения фронта кристаллизации вычислялись по формуле (2):

U 5 + U 6,

xk =     2    (tk - tl) •                   (2)

Для описания внешних силовых воздействий введём безразмерные критерии задачи: число Грасгофа Gr , безразмерную интегральную силу, действующую на металл со стороны бегущего магнитного поля F , и силовой параметр N , определяемый как отношение F/Gr .

В условиях температурной неоднородности в текущей среде может возникать тепловая конвекция. Необходимым условием для возникновения конвективных течений является наличие ненулевого угла между градиентом температуры в жидкости и направлением силы тяжести [7]. Интенсивность существующего течения зависит от величины перепада температуры, линейных размеров жидкого объёма и физических свойств самой жидкости, и может в обобщенном безразмерном виде характеризоваться числом Грасгофа (3):

_r g e ( T h - T c ) L Gr =, u²

где g – ускорение силы тяжести, β – коэффициент теплового расширения среды, L – линейный размер задачи, ν – кинематическая вязкость жидкости и ( T h – T c ) – перепад температуры между нагревателем ( T_h ) и холодильником ( T_c ).

Согласно [13; 14], величина планарной толкающей силы, действующей со стороны бегущего магнитного поля на проводящую среду, может быть выражена по формуле (4)

F = OtoTB0

^x 2n h ’

где B ₀ – величина индукции магнитного поля, ω – циклическая частота тока в индукторе бегущего магнитного поля, τ – шаг полюсов индуктора и h – толщина слоя проводника, по которой выполняется осреднение силы.

По аналогии с числом Грасгофа можно ввести безразмерный силовой критерий F , определяемый соотношением (5):

FL ³

F = x^— • pu

Безразмерный критерий N = F /Gr характеризует отношение сил электромагнитного перемешивания к силам, вызывающим свободно конвективный механизм перемешивания, и является безразмерным управляющим параметром задачи.

2.    Результаты

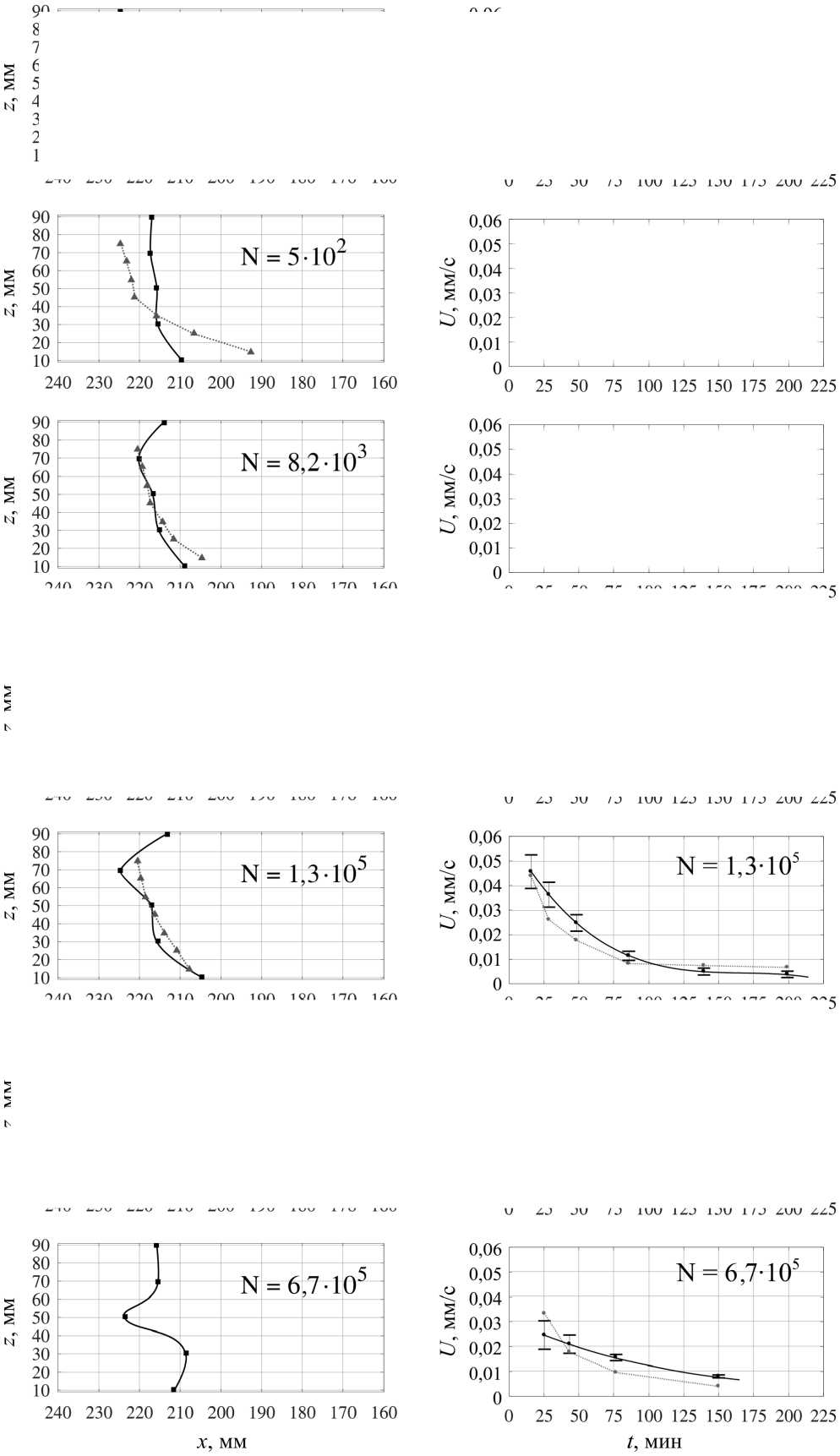
Под действием горизонтального градиента температуры металлический расплав претерпевает фазовый переход. Как уже отмечалось выше, в отсутствие внешнего перемешивания условия кристаллизации металла определяются свободно-конвективными потоками. Внешнее силовое воздействие изменяет условия теплообмена за счёт принудительного перемешивания жидкости. На рис. 5, a, приведены формы профилей кристаллизации, найденные при помощи ультразвукового и термопарного методов для различных режимов перемешивания жидкого металла внешним бегущим магнитным полем контролируемой интенсивности.

Значение силового параметра N = 0 отмечает режим, при котором перемешивание происходит исключительно за счёт тепловой конвекции (ЛИМ бездействует). Значения N , отличные от нуля, соответствуют разным величинам тока в обмотках ЛИМ и, соответственно, амплитуды бегущего магнитного поля.

Видно, что хорошее соответствие данных косвенного термопарного и прямого ультразвукового методов определения положения и формы фронта кристаллизации достигается при режимах принудительного перемешивания. В отсутствие перемешивания ( N = 0) и при самом слабоинтенсивном вынужденном течении ( N = 500) наблюдается расхождение показаний двух измерительных методик. По всей видимости, расхождение в показаниях двух методов обусловлено локальной кристаллизацией ограниченных объёмов галлиевого сплава около стенки в области расположения термопарных датчиков. Принудительное перемешивание предотвращает образование застойных зон с пониженной температурой, что приводит к лучшему совпадению термопарного метода с ультразвуковым.

Тем не менее даже в отсутствии принудительного перемешивания термопарный метод позволяет корректно определять темп кристаллизации металла. На рис. 5, b , представлены графики эволюции средней скорости движения фронта кристаллизации вдоль слоя для различных величин внешнего силового воздействия. Хорошо видно не только качественное, но и количественное согласие величин скоростей, найденных двумя методами. Кривые, соответствующие ультразвуковым измерениям, получены по датчику, который измеряет положение фронта кристаллизации по координате Z в области, наиболее близкой к расположению по этой же оси продольного ряда термопар. Следует отметить, что отмеченные на графиках разбросы ультразвуковых данных обусловлены различн ы ми показаниями по высоте слоя (с разных датчиков) и рассчитываются как среднеквадратичное отклонение скорости движения фронта от среднего по пяти значениям (по высоте).

Наибольшая неоднородность фронта кристаллизации по высоте (см. рис. 5, a ) наблюдается при N = 0, т.е. даже слабое перемешивание повышает однородность фронта кристаллизации, что согласуется с известными данными.

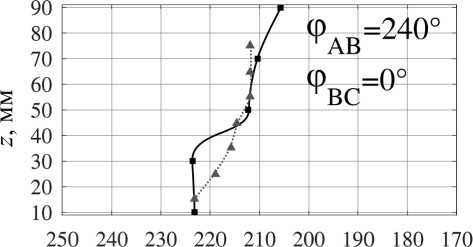
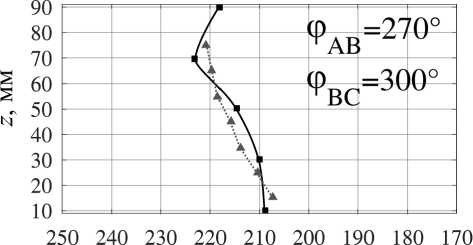
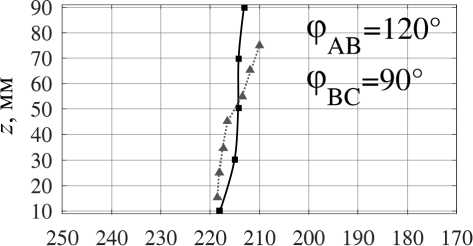
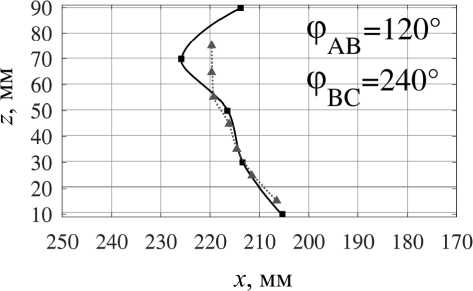
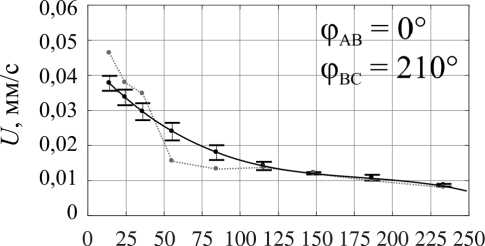
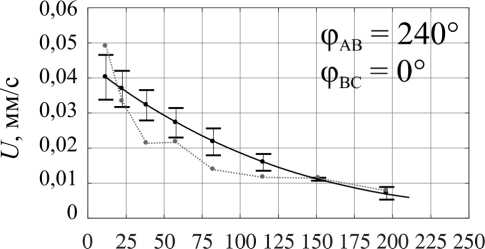
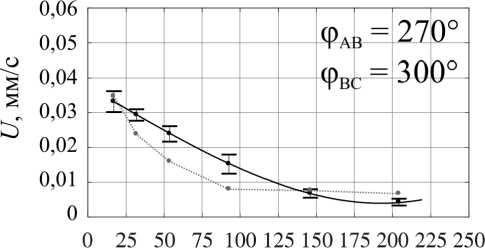
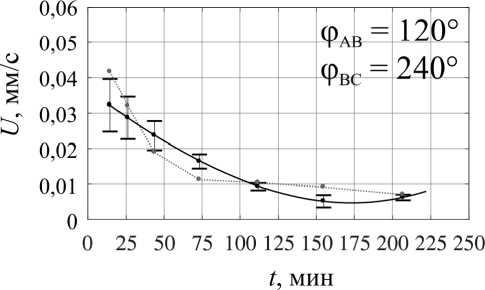
Изменение топологии объёмных сил и, как следствие, топологии возникающих в жидкой фазе течений возможно и посредством вариации фаз токов питания индуктора при неизменной их амплитуде. Мы рассмат- риваем несколько вариантов питания индуктора, обеспечивающих генерацию течений с различным количеством вихрей (мелкомасштабное многовихревое течение при φAB = 0°, φBC = 0°, малоинтенсивное четырёхвихревое течение при φAB = 0°, φBC = 210°, трёхвихревое течение при φAB = 240°, φBC = 0°, два крупномасштабных вихря при φAB = 270°, φBC = 300°, один крупномасштабный вихрь, охватывающий весь слой при φAB = 120°, φBC = 240°, и вихрь с реверсной закруткой при φAB = 120°, φBC = 90°), обеспечивающих подавление крупномасштабных течений при сохранении мелкомасштабного перемешивания [18].

Переходя к анализу формы фронта кристаллизации (рис. 6, a ), можно утверждать, что наибольшую однородность процесса обеспечивают режимы внешнего воздействия с фазовым набором φ _AB = 0°, φ _BC = 0° и φ AB = 120°, φ BC = 90°, соответствующие пульсирующему магнитному полю и мелкомасштабному перемешиванию и реверсивному крупномасштабному одновихревому течению соответственно. Во втором случае вынужденное течение направлено против конвективного потока и во многом компенсирует нежелательный теп-ломассоперенос.

На рис. 6, b , представлены зависимости средней скорости движения фронта кристаллизации вдоль слоя при различных режимах перемешивания жидкого металла. Наилучшее согласие данных двух методов наблюдается в режиме генерации мелкомасштабных течений пульсирующим полем (φ AB = 0°, φ BC = 0°). Тем не менее во всех рассмотренных режимах термопарные измерения позволяют корректно измерить средние скорости продвижения фронта кристаллизации и общие тенденции её эволюции.

Заключение

Было рассмотрено влияние амплитуды и топологии магнитного поля трёхфазного индукционного переме-шивателя на процесс направленной кристаллизации металлического расплава. Найдены темп и однородность кристаллизации в зависимости от параметров магнитного поля.

Изменение интенсивности электромагнитного воздействия позволяет существенно изменять темп кристаллизации и влиять на форму образующейся твердой фазы, что является интуитивно понятным и известным фактом. Интерес представляет воздействием магнитных полей более сложной топологии при постоянстве величины воздействия. Изменение фазных углов токов трёхфазного перемешивателя позволяет генерировать в жидком металле вихревые течения различной топологии, в частности, изменять количество крупномасштабных вихрей или подавлять крупномасштабное течение. Влияние гидродинамических потоков изменяет форму фронта кристаллизации, предоставляя возможность управления однородностью затвердевания металла

b

a

Рис. 5. Форма фронта кристаллизации ( а ) и изменение среднего темпа кристаллизации со временем ( b ), измеренные при помощи УДА (черная сплошная линия) и термопарных датчиков (красная пунктирная линия), при различный значениях параметра силового воздействия

								?
				I	4 =	5,С	НС
								—

								з
				т	ч —	8,2	/1С

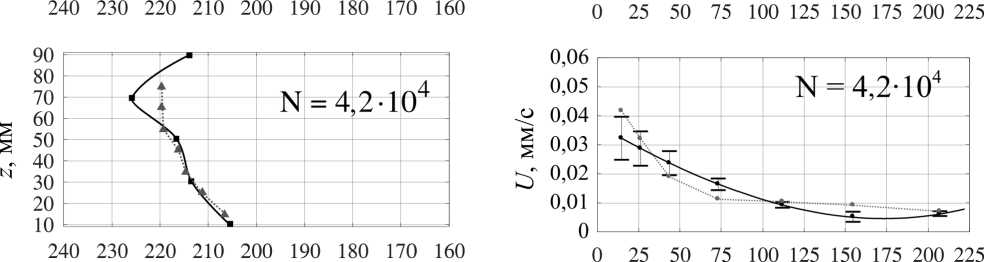
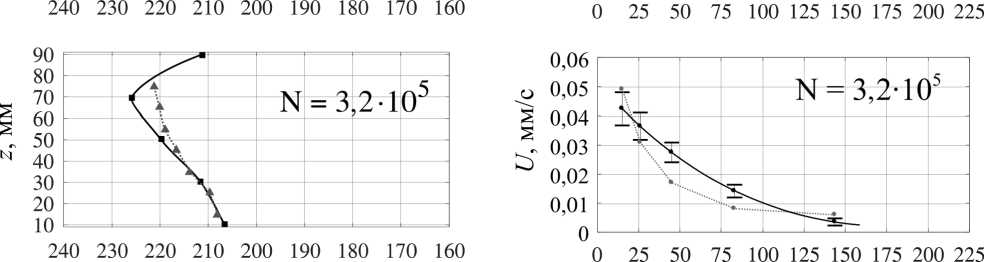
Fig. 5. The crystallization front shape ( а ) and the change in the average crystallization rate with time ( b ), measured using UDV (solid black line) and thermocouple sensors (red dotted line) at different values of the force parameter

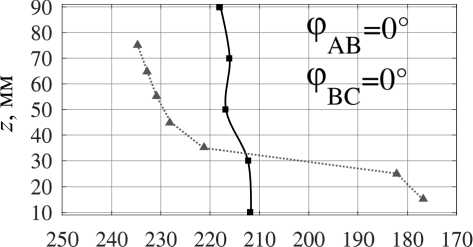
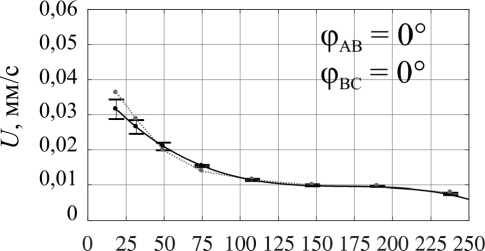
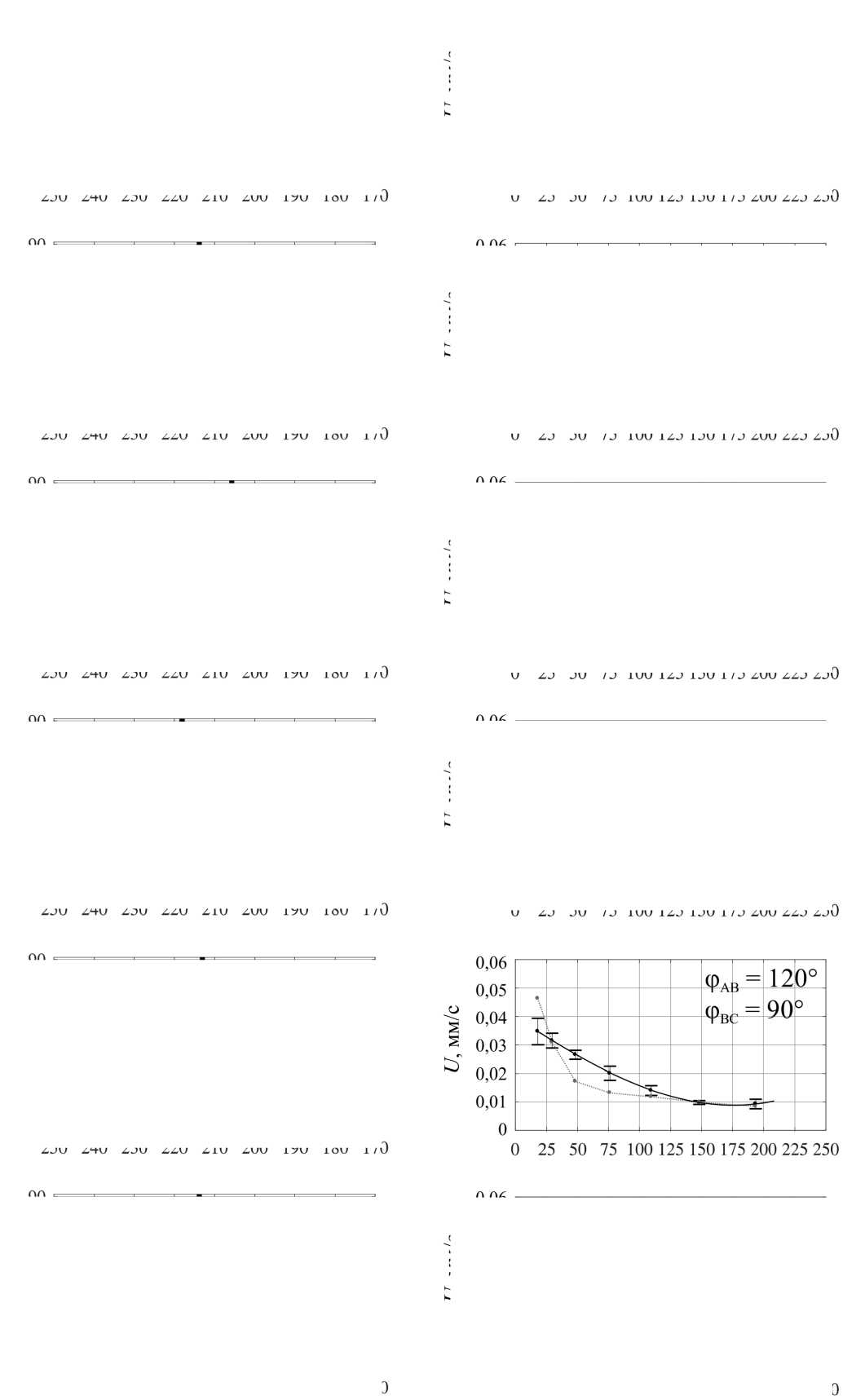
Рис. 6. Форма фронта кристаллизации ( а ) и изменение среднего темпа кристаллизации со временем ( b ), измеренные при помощи УДА (черная сплошная линия) и термопарных датчиков (красная пунктирная линия), при различных значениях фаз токов питания

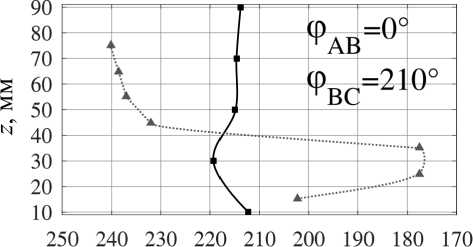
a

b

Fig. 6. The crystallization front shape (а) and the change in the average crystallization rate with time (b), measured using UDV (solid black line) and thermocouple sensors (red dotted line) at different values of current phases посредством изменения характеристик питания индуктора. Важно отметить, что изменение фазных углов токов при сохранении амплитуды питания не оказывает существенного влияния на темп кристаллизации, что открывает широкие возможности контроля процессов за счет изменения как силы тока, так фазных углов.

Был успешно применён и верифицирован по измерениям датчиками ультразвукового анемометра температурный метод определения положения фронта кристаллизации.