Анализ гармонического состава токов и напряжений дуг в дуговой сталеплавильной печи с использованием математической модели

В настоящее время в современной металлургической промышленности наблюдается активная тенденция по увеличению доли жидкой стали, полученной с использованием дуговых сталеплавильных печей (ДСП) и установок ковш-печь (УКП). Это обусловлено высокими показателями качества готовой продукции, а также высокими техникоэкономическими показателями работы, достигаемыми в процессе эксплуатации печных агрегатов данного типа. Несмотря на очевидные преимущества, ДСП остаётся одним из самых ёмких потребителей электроэнергии, поскольку удельная мощность печного трансформатора для современных агрегатов достигает величины 0,7–1 МВА/т при номинальной массе выплавляемой стали от 100 до 250 т [1]. В связи с этим особую актуальность приобретает задача оптимизации работы ДСП с целью снижения производственных издержек путём сокращения затрат электроэнергии в процессе плавления. Существует несколько путей решения данной задачи, одним из которых является совершенствование систем управления электрическими режимами работы печи. Как правило, все существующие системы управления электрическим режимом ДСП обладают двухуровневой структурой. На втором уровне в соответствии с профилем плавки формируется задание ступени печного трансформатора NТР, реактора NР (при наличии) и номера рабочей кривой NРК. При этом критерием перехода с одной стадии плавки на другую в подавляющем большинстве случаев являет- ся показатель удельного расхода электроэнергии WУД. Сочетания NТР и NР определяют форму электрических, рабочих и технологических характеристик, в том числе отражающих зависимость мощности электрической дуги PД от тока дуги IД, тем самым позволяя регулировать объём электрической энергии, вводимой в печь. В свою очередь, параметр NРК определяет текущий набор уставок параметра регулирования в системе управления первого уровня, определяя рабочую точку на электрической характеристике PД = f(IД) и обеспечивая её поддержание за счёт управления гидравлическим приводом перемещения электродов [2]. Аналогичным образом контролируются значения коэффициента износа футеровки КИФ = f(РД, IД) и коэффициента интенсивности нагрева КИН = f(РД, IД).

Подавляющее большинство современных систем управления электрическим режимом, таких как ARCOS, Simelt (Primetals Technologies, ранее Siemens VAI, VAI Fuchs, Vantron, Германия), HI-REG Plus, Q-REG (Danieli, Италия), E.M.P.E.R.E (Amec Spie, Франция), DECTEQ (Ferrotron, Германия) и Digit Arc (AMI, Мексика)), обладают потенциалом к внедрению усовершенствованных алгоритмов управления как для системы второго, так и для системы первого уровня.

В рамках данного исследования рассматривается усовершенствованный алгоритм управления электрическим режимом ДСП в составе системы второго уровня, в основе которого лежит альтернативный способ диагностики стадии плавления металлошихты с использованием информации о высших гармониках токов и напряжений электрических дуг. Основная цель применения данного алгоритма – обеспечение своевременных переключений сочетаний NТР, NР и NРК в соответствии с реальной технологической стадией плавления ме-таллошихты в ДСП, что обеспечивает снижение затрат электроэнергии за цикл плавки. В основе данного алгоритма лежит раздельный анализ чётныx и нечётныx гармоник токов и напряжений дуг. Отметим, что главной задачей исследований поведения чётных и нечётных гармоник является выявление зависимостей между иx уровнем в составе сигнала тока и напряжения дуги и технологической стадией плавления металлошихты.

Теоретические основы применения анализа гармонического состава напряжения электрической дуги для системы диагностики стадии плавления металлошихты

Как отмечалось ранее, подавляющее большинство современных систем управления электрическим режимом обладают рядом недостатков, которые открывают пути к внедрению усовершенствованных алгоритмов. В работе [2] был прове- дён подробный анализ наиболее распространённых в России и за рубежом систем, в ходе которого был сформирован перечень критериев, на основе которых можно судить об обеспечении той или иной системой энергоэффективного управления печным агрегатом. Также в ходе анализа было установлено, что ни одна из существующих систем управления электрическим режимом не удовлетворяет критерию наличия возможности диагностики стадий плавки в ДСП (оценка стабильности нагрева стали в УКП) и интеллектуального управления процессом переключения ступеней РПН трансформатора NТР, реактора NР и изменения рабочих кривых NРК. Это связано с тем, что во всех рассматриваемых системах использовался профиль плавки, в структуре которого заложен переход с одного сочетания NТР, NР и NРК на другое по мере достижения определённых критических значений удельного расхода электроэнергии WУД. В качестве поясняющего примера в таблице приведена структура профиля плавки для системы ARCOS, функциональная схема которой представлена на рис. 1.

Основной недостаток использования величины W _У Д в составе профиля плавки заключается в

Структура профиля плавки в системе управления электрическим режимом ARCOS (Siemens VAI, Primetals Technologies)

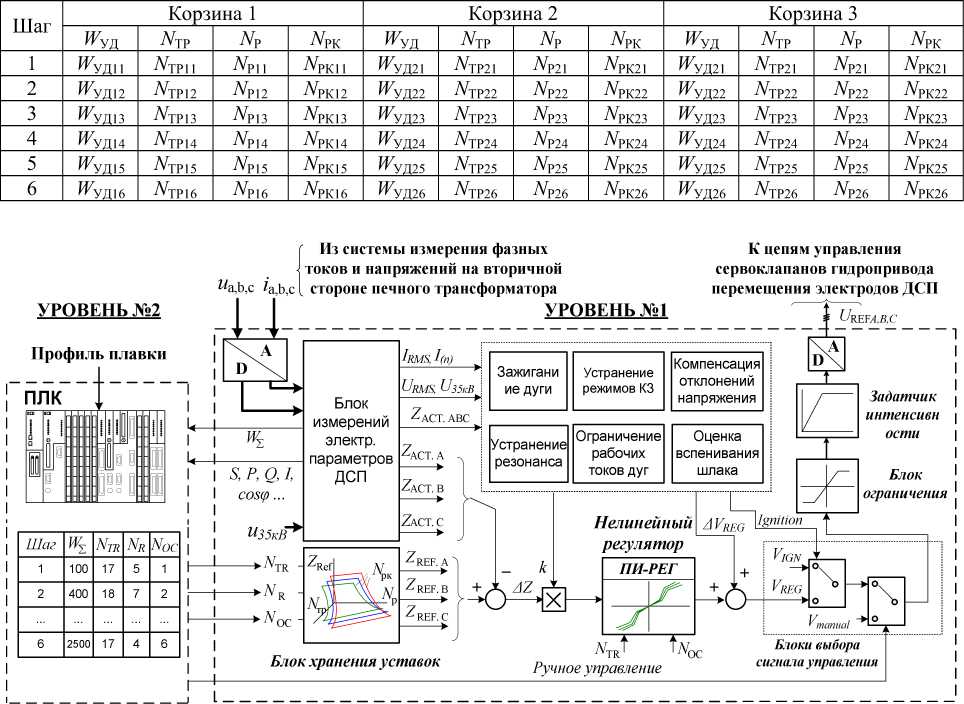
Рис. 1. Функциональная схема системы управления электрическими режимами ДСП ARCOS (Siemens, Германия)

том, что данный параметр не имеет прямой связи с реальными технологическими процессами, протекающими внутри ванны печи. Определение граничных значений WУД в составе профиля осуществляется на основе количественной, а не качественной оценки лома, используемого в завалке и подвалках. По различным причинам состав металло-шихты меняется от плавки к плавке, вследствие чего достоверно оценить стадию плавки основываясь лишь на данных о количестве лома и введенной энергии достаточно сложно. Так, для одинакового количества металлошихты с ломом и скрапом по достижении одного и того же граничного значения WУД, фактические стадии расплавления могут быть неодинаковыми: в одном случае уже может идти основная стадия расплавления, в другом – только завершаться стадия проплавления колодцев. Таким образом, разработка усовершенствованного профиля плавки, обеспечивающего адекватное переключение сочетаний NТР, NР и NРК в соответствии с текущей стадией плавления, является актуальной задачей, решение которой позволит повысить энергоэффективность работы ДСП.

Основной проблемой на пути к решению данной задачи является выбор критерия, в соответствии с которым будут производиться переключения. В качестве решения данной проблемы, в работе [3] было предложено в качестве основного критерия использовать суммарный коэффициент гармонических составляющих тока дуги KI. В ос- нове идеи применения данного критерия лежат физические свойства электрической дуги, речь о которых пойдёт далее.

Электрическая дуга в математическом выражении может быть представлена дифференциальным уравнением мгновенной проводимости (уравнением Касси) [4]:

@ ( t ) dg^ = ( u ^ -1) g ( t ) dt , (1)

Д dt EД2 (t) Д где gД(t) – мгновенное значение проводимости электрической дуги; ΘД – тепловая постоянная времени электрической дуги; EД(t) – противоЭДС электрической дуги.

ПротивоЭДС электрической дуги, в свою очередь, определяется по следующей формуле

E Д =

K ВЭ ^{( a} + P L д ), i д ⁽ t ) >  0; a + p L д, i д ⁽ t ) <  0,

где α – падение напряжения в приэлектродных областях; β – градиент напряжения дугового столба; L Д – длина электрической дуги; K _ВЭ – коэффициент вентильного эффекта.

Тепловая постоянная времени электрической дуги ΘД и KВЭ являются параметрами, наиболее тесно связанными со стадией плавки. Величина ΘД по мере расплавления твердой шихты и образования жидкой фазы, экранированной вспененным шлаком, постепенно изменяется в диапазоне от 250 до 3500 мкс. Параметр KВЭ, определяющий отношение величины противоЭДС дуги в момент прохождения положительной полуволны мгновенного значения тока дуги к величине противоЭДС дуги в момент прохождения отрицательной полу- волны, по мере проплавления изменяется в диапазоне от 1,2 до 1 [5]:

K r з =

ВЭ

E Д +

E Д

I m Д +

I m Д —

где EД+, EД– – противоЭДС дуги в период прохождения положительной и отрицательной полуволн тока дуги соответственно; ImД+, ImД– – амплитуда положительной и отрицательной полуволн сигнала мгновенного значения тока дуги соответственно.

Таким образом, идея применения коэффициента несинусоидальности кривой тока дуги K_I для решения задачи диагностики стадии плавления шихты основана на том, что по мере роста величины Θ Д и уменьшения K _ВЭ доля высших гармоник в составе тока электрической дуги снижается.

Данная идея получила своё развитие в исследовании [6], где был проведён подробный анализ гармонического состава сигнала тока электрической дуги на печных агрегатах различного класса и мощности. В результате данного исследования было предложено использовать для решения задач диагностики стадии плавки раздельный анализ по относительным действующим значениям чётных I’ Д.ВГ.ЧЁТ.Σ и нечётных I’ Д.ВГ.НЕЧЁТ.Σ гармоник. Экспериментальные исследования показали, что скорость ослабления чётных гармоник в начале приблизительно в четыре раза выше, чем нечётных. Вследствие этого использование чётных гармоник предпочтительнее использовать для диагностики стадии в начале плавки, а нечётных гармоник – в конце.

Параллельно исследованиям в области, посвящённой анализу гармонического состава токов дуг, развивались исследования в области применения гармонического состава напряжений дуг для решения задач диагностики стадии плавки. В исследовании [7] было предложено использовать в аналогичных целях коэффициент несинусоидаль-ности кривой напряжения дуги K_U . Основным преимуществом использования K U является меньшая зависимость данного параметра от колебаний длины электрической дуги и несимметричных режимов, вследствие чего снижается дисперсия результирующего сигнала и не возникает необходимости использования фильтров сигнала с большими постоянными времени, приводящих к искажениям и невозможности диагностировать непродолжительные стадии.

Отметим, что концепция раздельного анализа чётных и нечётных гармоник также применима и для сигнала напряжения дуги, что было обоснова- но в работе [6]. В данном исследовании также нашли своё экспериментальное подтверждение утверждения о меньшей зависимости гармонического состава напряжения дуги от длины дуги и несимметричных режимов.

Помимо преимуществ, которые предоставляет применение анализа гармонического состава напряжений дуг, существуют определённые недостатки. Величину мгновенного значения напряжения дуги проблематично измерить напрямую, вследствие этого необходимо прибегать к косвенному расчёту, для выполнения которого необходимы большие вычислительные мощности и точное определение параметров схемы замещения [8]. Кроме того, при относительно низкой интенсивности возмущающих воздействий и режимах горения дуг, близких к симметричным, выше обозначенные преимущества нивелируются.

Таким образом, как гармонический анализ тока, так и гармонический состав напряжения дуги могут быть использованы в качестве показателя для применения в системе диагностики стадии плавления шихты. Несмотря на достаточно большой опыт работы в данном направлении, остаётся неизученным вопрос, связанный с влиянием тепловой постоянной времени дуги Θ Д , коэффициента вентильного эффекта K _ВЭ, длины электрической дуги L Д _– и коэффициента несимметрии токов дуг K _2I на чётные и нечётные гармоники в отдельности. Подобный анализ проводился в исследовании [7], но только для величин K_I и K_U . Кроме того, ранее анализ в части чётных и нечётных гармоник преимущественно проводился на основе экспериментальных данных и нуждается в унификации на математической модели.

Анализ относительных действующих значений суммарных, чётных и нечётных гармоник токов и напряжений электрических дуг на основе математической модели

Для проведения анализа характера изменения чётных и нечётных гармоник тока и напряжения дуги была использована математическая модель электрического контура ДСП, разработка которой детально описана в работах [9–12]. В качестве объекта исследования выбрана дуговая сталеплавильная печь шахтного типа с мощностью печного трансформатора 85 МВА со следующими основными параметрами: ступень печного трансформатора N _ТР = 8, линейное напряжение на первичной стороне U _1Л = 35 кВ; линейное напряжение на вторичной стороне U 2Л = 847 В; коэффициент трансформации ПТ K _Т = 41,322; активное сопротивление питающей сети, приведённое к первичной стороне R_S = 0,135 Ом; индуктивность питающей сети, приведённая к первичной стороне L_S = 4,302 мГн; активное сопротивление обмотки ПТ, приведённое к первичной стороне R _ТР1-3 = 0,0994 Ом; индуктивное сопротивление обмотки ПТ, приведённая к первичной стороне L _ТР1-3 = 7,534 мГн; активное сопротивление участка короткой сети R КС1 = 0,303 мОм; R КС2 = 0,240 мОм; R _КС3 = 0,286 мОм; индуктивное сопротивление участка короткой сети L _КС1 = 8,929∙10^–6 Гн; L КС2 = 8,766∙10^–6 Гн; L КС3 = 8,703∙10^–6 Гн.

Для расчёта сигналов относительного действующего значения чётных и нечётных гармоник токов и напряжений дуг использована вспомогательная математическая модель, реализованная в среде MATLAB Simulink, функциональная схема которой представлена на рис. 2. В качестве входных

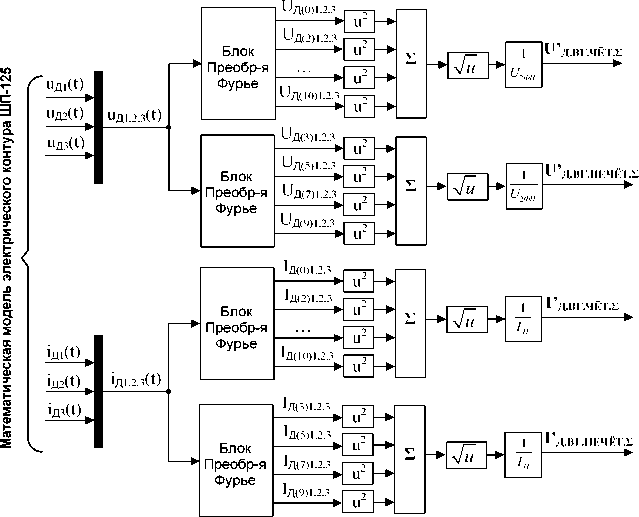
Рис. 2. Функциональная схема математической модели для расчёта относительных действующих значений чётных и нечётных гармоник токов и напряжений дуг

параметров для данной модели используются сигналы мгновенных значений токов i Д1 ( t ), i Д2 ( t ), i Д3 ( t ) и напряжений дуг u Д ₁( t ), u Д ₂( t ), u Д ₃( t ), формируемых в математической модели электрического контура.

В основу данной функциональной схемы заложены следующие расчётные формулы относительного

действующего значение суммарных чётных и нечётных гармоник тока и напряжения дуги:

I Д(0) ⁺ I Д(2) ⁺ I Д(4) ⁺ I Д(6) ⁺ I Д(8) ⁺ I Д(10)

I Д.ВГ.ЧЁТЁ =                      ,                        - ¹⁰⁰ %;

I _Н

U Д(0) + U Д(2) ⁺ U Д(4) ⁺ U Д(6) ⁺ U Д(8) ⁺ U Д(10)

U Д.ВГ.ЧЁТЁ =                                                - ¹⁰0 %,

U 2ФН

где I Д(0) , I Д(2) , I Д(4) , I Д(6) , I Д(8) , I Д(10) – действующие значения 0, 2, 4, 6, 8 и 10 гармоник тока электрической дуги соответственно; U Д(0) , U Д(2) , U Д(4) , U Д(6) , U Д(8) , U Д(10) – действующие значения 0, 2, 4, 6, 8 и 10 гармоник напряжения электрической дуги соответственно; I Н – номинальный ток печного трансформатора на текущей

ступени РПН; U 2Н – номинальное фазное напряжение печного трансформатора на текущей ступени РПН:

I Д .ВГ.НЕЧЁТЁ

Д(3) ⁺ I Д(5) ⁺ I Д(7) ⁺ I Д(9) --100 %;

I _Н

^U Д Л1.НЕЧЁТ1

^ГД(3) ^{+ U} Д(5) ^{+ U} Д(7) ^{+ U} Д(9) --100 %,

U 2ФН

где I Д(3) , I Д(5) , I Д(7) , I Д(9) – действующие значения 3, 5, 7 и 9 гармоник тока электрической дуги соответственно; U Д(3) , U Д(5) , U Д(7) , U Д(9) – действующие значения 3, 5, 7 и 9 гармоник напряжения электрической дуги соответственно.

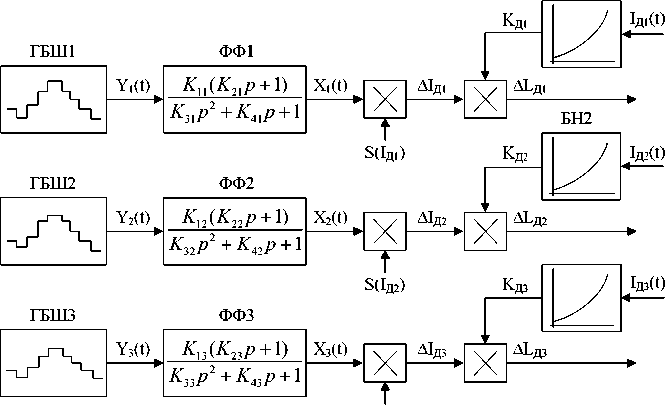
На математической модели, функциональная схема которой представлена на рис. 3, было выполнено исследование влияния тепловой постоянной времени дуги, вентильного эффекта, а также несимметричных режимов на чётные и нечётные гармоники токов и напряжений дуг. При проведении исследований получе-

ны следующие осциллограммы:

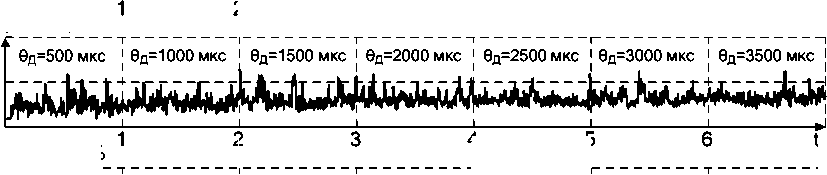
• 1)    средние по трём фазам значения величин I ^ДВГЧЁТ , I д_Вгнечёт, U д_ВГЧёт, U д _ВГ нечёт при ступенчатом изменении величины Θ Д от 500 до 3500 мкс с шагом 500 мкс, постоянной величине K _ВЭ = 1,2 и одинаковой длине электрической дуги в трёх фазах, равной 400 мм;

• 2)    средние по трём фазам значениям величин I Д. _ВГ . _ЧЁТ , I Д. _ВГ . _НЕЧЁТ , U Д. _ВГ . _ЧЁТ , U Д. _ВГ . _НЕЧЁТ при ступенчатом изменении величины K _ВЭ от 1,2 до 1,00 с шагом 0,05, постоянной величине Θ Д = 500 мкс и одинаковой длине электрической дуги в трёх фазах, равной 400 мм;

• 3)    значения I _{Д.ВГ.ЧЁТ} , I _{Д.ВГ.НЕЧЁТ} , U _{Д.ВГ.ЧЁТ} , U _{Д.ВГ.НЕЧЁТ} для каждой из трёх фаз в отдельности при ступенчатом изменении величины длины электрической дуги в фазе «3» от 200 до 700 мм при постоянной длине дуги в фазах «1» и «2», равной 100 мм.

БН1

ЗОдз)

Рис. 3. Функциональная схема блока формирования случайных возмущений электрических дуг

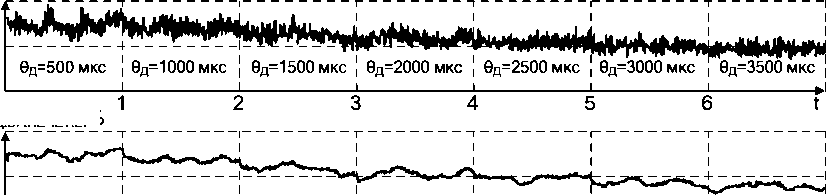
Осциллограммы, полученные в результате моделирования, представлены на рис. 4–7. Отметим, что для достижения в процессе моделирования режимов работы, максимально приближенных к реальным, в модели была использована система формирования случайных возмущений по длине электрической дуги по аналогии с той, что была разработана в [13]. Функциональная схема данной системы приведена на рис. 3.

и'д.ВГ.ЧЁТ.Г,%

a) 5

t,c

0д=5ОО мкс 10д=1ОООмкс I 0д=15ООмкс I 0д=2ОООмкс I 0д=25ООмкс 10д=ЗОООмкс I 0д=35ОО мкс I

о и'д.вГ.НЕЧЁТ.Е.%

6) 20

О'---------

t,c

1'д.ВГ.ЧЁТ.Е,% 10

в) 5

t,c

О

1'ДВГ.НЕЧЁТ.Г,%

Г) 5

0д=5ООмкс i 0д=1ОООмкс I 0д=15ООмкс1 0д=2ООО мкс I 0д=25ОО мкс I 0д=ЗОООмкс! 0д=35ООмкс!

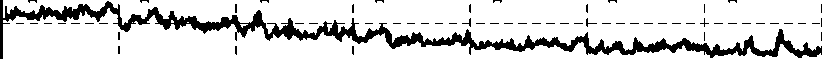
t,c

Рис. 4. Осциллограммы средних по 3 фазам относительных действующих значений суммарных чётных и нечётных гармоник: а, б – напряжения дуги; в, г – тока дуги при ступенчатом изменении величины θД в симметричном режиме и'д.вГ.ЧЁТ.Ь%

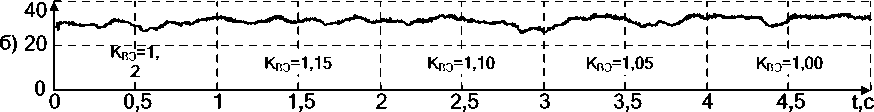
1'дВГ.ЧЁТ.Е,%

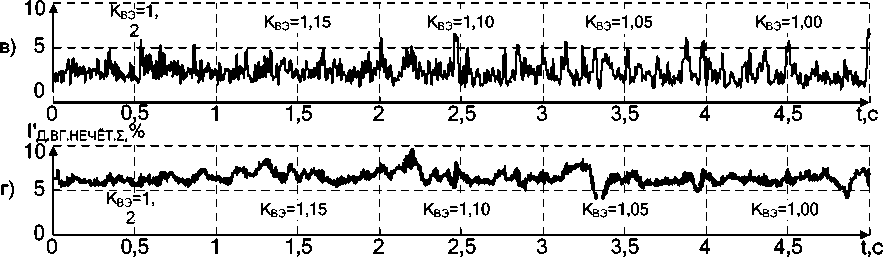
Рис. 5. Осциллограммы средних по 3 фазам относительных действующих значений суммарных чётных и нечётных гармоник: а, б – напряжения дуги; в, г – тока дуги при ступенчатом изменении величины K ВЭ в симметричном режиме

20, 6) 10 о	и д.вг.чёт.52, /о                                 Фаза «2» .                                                                   I                                                                     I                                                                     I                                                                     I                                                                     I                                                                      I 1_дз=200 мм ।    1_дз=300 мм ।   1_дз=400 мм ।   1_дз=500 мм ।   1_дз=600 мм ।   1_дз=700 мм ।
20,	0               1               2               3               4               5              1, и'д.вг.чЁт.73,%                               Фаза «3»
10	1_дз=200 мм 1    1_дз=300 мм 1   1_дз=400 мм 1   1_дз=500 мм 1   1_дз=600 мм 1   1_дз=700 мм 1
в) 0	1                                              1                                              1                                              1                                              1                                            .1

a)

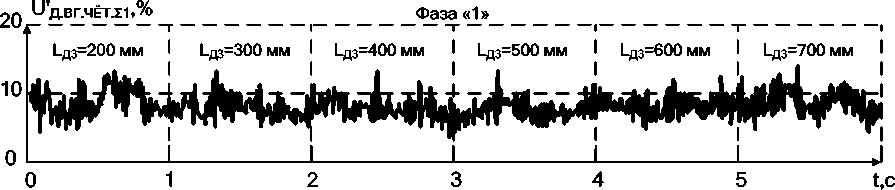
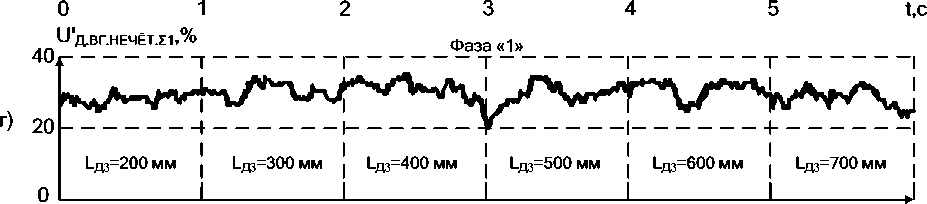
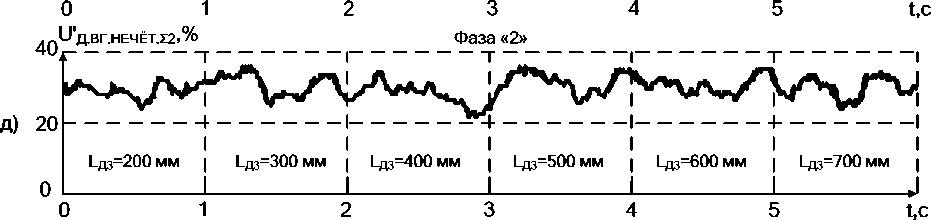
Рис. 6. Осциллограммы относительных действующих значений суммарных чётных и нечётных гармоник напряжения дуги по каждой из 3 фаз для: а, б, в – чётных гармоник; г, д, е – нечётных гармоник при ступенчатом изменении величины длины электрической дуги в фазе «3»

1^,д.вг.чёт.еъ%                               Фаза«1»

--------г------!-------г------!-------г

Ьдз=200 мм I 1_дз=300 мм I 1_дз=400 мм I 1_дз=500 мм I 1дз=600 мм I 1дз=700 мм I

Фаза «2»

30 1'д.ВГ.ЧЁТ.12,%

1_дз=400 мм

1_дз=500 мм

1дз=600 мм

1дз=700 мм

о

Ьдз=200 мм |   1дз=300 мм

б)

в

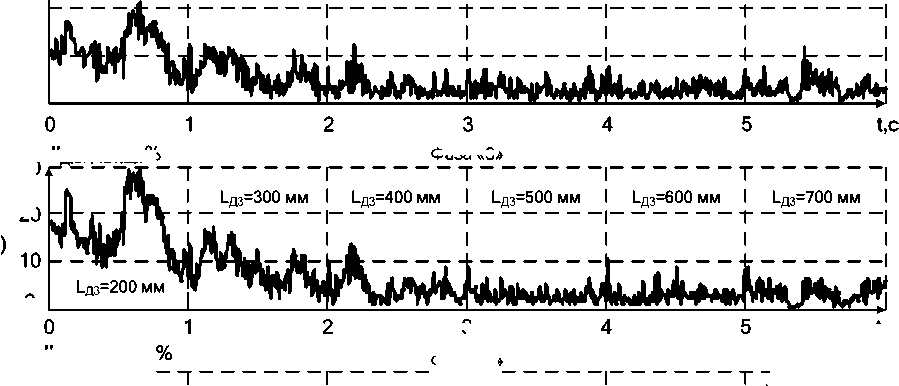
Фаза «3»

2Q 1'д.ВГ.ЧЁТ.73,%

О t,c

Фаза «1»

1дз=700 мм

1дз=600 мм

|    j            |                  |                  |   кдз=Ьии ММ |  чдз-/иимм ।

Д.ВГ.НЕЧЁТ.П, 1Э------

г)

О

1 дз=200 мм  I   1 дз=300 мм  |  1 дз=400 мм   |  1 дз=500 мм |Г               j

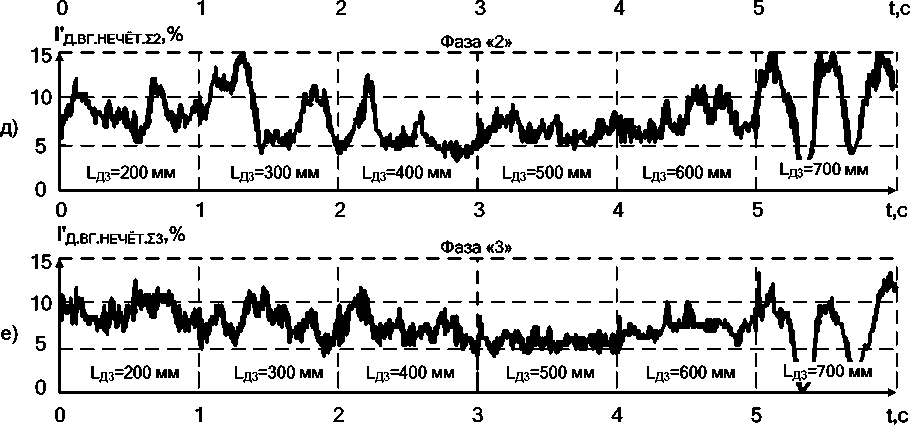
Рис. 7. Осциллограммы относительных действующих значений суммарных чётных и нечётных гармоник тока дуги по каждой из 3 фаз для: а, б, в – чётных гармоник; г, д, е – нечётных гармоник при ступенчатом изменении величины длины электрической дуги в фазе «3»

Анализ осциллограмм позволил получить теоретическое подтверждение для следующих выводов.

• 1.    В симметричном режиме, когда длины дуг одинаковы, величины Θ Д в наибольшей мере влияет на нечётные гармоники, а изменение K _ВЭ, в свою очередь, влияет на чётные гармоники. При этом в обоих случаях сигналы относительного действующего значения суммарных чётных и нечётных гармоник более стабильны для напряжения электрической дуги, вследствие чего при использовании в системе управления нуждаются в меньшей величине постоянной времени сглаживающего фильтра.

• 2.    Несимметричные режимы работы оказывают сильное влияние на чётные и нечётные гармоники тока электрической дуги, в то время как гармоники напряжения дуги данному влиянию подвержены в значительно меньшей мере, что осложняет применение анализа гармонического состава [14–23] токов дуг для решения задач диагностики стадии плавления шихты на начальных стадиях ввиду необходимости применения сглаживающих фильтров с большой постоянной времени, что приведёт к потерям информации о непродолжительных стадиях.

Заключение

• 1.    Использование информации о гармоническом составе токов и напряжений дуг является перспективным направлением в развитии усовершенствованных систем управления электрическим режимом ДСП и УКП с интеллектуальной системой диагностики технологических стадий плавки. В ходе исследований с использованием математической модели теоретически обоснована тесная связь между уровнем нечётных гармоник тока и напряжения дуги и тепловой постоянной времени, а также связь между уровнем чётных гармоник и величиной коэффициента вентильного эффекта. Показано, что величина вентильного эффекта изменяется от максимального к минимальному значению по мере полного расплавления твёрдой шихты, а величина тепловой постоянной времени достигает максимального значения при экранировании дуг вспененным шлаком, что характерно

• 2.    Результаты математического моделирования подтвердили эффективность построения системы диагностики стадии плавления шихты, в соответствии с которым анализ чётных гармоник используется в начале плавки, а нечётных гармоник – в конце. Кроме того, для гармоник напряжений электрических дуг доказана меньшая зависимость изменения уровней гармоник при колебаниях длин электрических дуг и их несимметрии, чем у гармоник тока дуг, что является важным преимуществом используемого способа диагностики стадий расплавления металлошихты.

• 3.    Информация о гармоническом составе тока электрической дуги, такжекак и гармоническом составе напряжения дуги, может быть использована при разработке системы диагностики стадии плавления металлошихты. При этом анализ гармонического состава тока предпочтительнее использовать на сталеплавильных агрегатах, где используется режим горения дуг, близкий к симметричному, а также агрегатов с низкой интенсивностью возмущающих воздействий (например, печей с технологией непрерывной подвалки шихты конвейером, установок ковш-печь). Анализ гармонического состава напряжения дуги больше подходит для установок с сильными возмущающими воздействиями, а также значительным влиянием несимметричных режимов (шахтные печи, печи с классической завалкой через отводимый свод). В иных случаях применение вычислительных мощностей для расчёта мгновенного значения напряжения дуги нецелесообразно ввиду одинаковой эффективности применения анализа гармоник тока дуги.

для стадии доводки. Таким образом, было сделано теоретическое обоснование для полученных ранее экспериментальных зависимостей изменения гармонического состава токов и напряжений дуг от стадий плавки. В частности, доказано, что сокращение доли чётных гармоник в составе сигналов токов и напряжений дуг в начале плавки происходит существенно быстрее, чем сокращение доли нечётных гармоник.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (проект № FZRU-2020-0011).