Анализ гидрофизических свойств почв с использованием поросетевых моделей

7 Bld. 2 Pyzhevskiy per., Moscow 119017, Russian Federation, *, e-mail: , **, e-mail: , ***, e-mail:

1 Bld. 10 B. Gruzinskaya Str., Moscow 12324210, Russian Federation, ****, e-mail:

Структура почвы и ее порового пространства – фундаментальная характеристика, которая оказывает влияние на физические (Miranda-Velez et al., 2023), химические (Vogel et al., 2022) и биологические (Gui-Yuan, Hao-Ming, 2014) свойства почвы. Структура почвы оказывает важнейшее влияние на сельскохозяйственные свойства почвы и играет важную роль в перемещении и запасании влаги (Vogel et al., 2022), усвоении почвой удобрений (Bronick, Lar, 2005), эмиссии газов (Ball, 2013) и секвестрации углерода (Kay, 2018; Rabot et al., 2018).

Концептуальные модели, использующиеся в современной физике почв, предполагают, что структура порового пространства является статичной и именно в таком представлении используется в моделировании гидрофизических свойств (Van Genuchten, 1980; Шеин, 2005; Radcliffe, Simunek, 2018). Развитие новых методов визуализации и изучения почвенной структуры, включая рентгеновскую компьютерную томографию, позволило продвинуться в понимании ее динамики. Недавние эксперименты показывают, что структура почвы может подвергаться изменениям вплоть до нескольких раз в течение суток в результате изменения влажности (Fomin et al., 2023), колебаний температур (Tolstygin et al., 2025) и т. д. Высокая динамичность почвенной структуры заставляет задать вопрос: что почвенная структура представляет из себя per se , то есть как и каким образом структура порового пространства выглядит в текущий момент времени?

Почвенная структура описывается различными способами, которые учитывают функциональные, геометрические, пространственные свойства объекта (Шеин, 2005). В смежных с почвоведением областях науки: геофизике, геологии, нефтегазовом деле, структуру порового пространства пород представляют в виде графа, в котором вершины графа соответствуют порам, а ребра – тонким вытянутым пустотам или каналам, связывающим поры

(Lenormand et al., 1983). С развитием компьютерной рентгеновской томографии стало возможным исследовать непосредственную структуру горных пород, появились методы извлечения графов, называемых поросетевыми моделями (Zubov et al., 2022). Первые исследования по работе с пористыми средами в формате графов были проведены в восьмидесятых годах прошлого столетия (Lenormand et al., 1983). Подобное представление кажется заведомо более приближенным к реальности, поскольку позволяет учитывать структуру образца в текущий момент времени и сравнивать структуры образцов в разных состояниях.

Поросетевые модели пористых сред – это представление порового пространства пористого тела в виде связного графа, где вершины графа представляют собой поры, а ребра графа – каналы, связывающие эти поры. ПСМ используются для моделирования однофазной и двухфазной проницаемостей – определении коэффициентов фильтрации и влагопроводности (Blunt, 2011; Gerke et al., 2024). Они также применяются в моделировании поведения флюидов в нанопорах (Yang, 2019). Представление порового пространства в виде графа может быть использовано для исследования морфологических свойств образца (Tolstygin et al., 2025). Поросетевое моделирование может быть использовано для изучения морфологических задач и задач динамики флюидов в пористой среде, включая моделирование гистерезиса (Ahrenholz, 2008), исследование сорбции флюидов (Xu, Prodanović, 2018), анализ связности порового пространства (Bernabé et al., 2010), исследование распределения пор по размерам (Vogel, 2000; Gerke, 2024; Tolstygin et al., 2025), получение капиллярных кривых (Vogel, 2000; Gerke, 2024), исследование поведения газов (Mahabadi et al., 2016). Современные методы извлечения ПСМ позволяют сохранять и анализировать топологию порового пространства (Zubov et al., 2022).

Изучение возможностей и областей применения ПСМ, их сравнение с классическими методами физики почв являются задачами переднего края науки с учетом обширного накопленного опыта в области микротомографии порового пространства почвы зарубежных и отечественных исследователей (Герке и др., 2012; Романенко и др., 2017; Иванов и др., 2019; Абросимов и др., 2021).

В этой статье раскрываются основные принципы работы поросетевых моделей и проводится сравнение гидрофизических характеристик почвы, измеренных традиционными методами и полученных методами поросетевого моделирования. Дополнительно в рамках работы будут затронуты методические аспекты работы с ПСМ, включая детали извлечения графов ПСМ из 3D-изображений микротомографии образцов почвы.

ОБЪЕКТЫ И МЕТОДЫ

Отбор образцов, определение почвенных свойств

Полевой этап исследования был проведен в Центральном черноземном заповеднике имени В.В. Алёхина в Курской области. Почва участка косимой степи была классифицирована как чернозем миграционно-мицеллярный (Полевой определитель почв России, 2008), Greyzemic Chernozem (Loamic, Pachic) (WRB, 2022). Отбор ненарушенных образцов (монолиты) был проведен из трех почвенных горизонтов – AUrz, AU, BCA с глубин 20, 40 и 80 см соответственно. Образцы были аккуратно отобраны в полипропиленовые трубки диаметром 20 мм и высотой 5 мм. Процедура пробоотбора выглядела следующим образом: 1) вырезка куба 5 × 5 × 5 см3 из подготовленного почвенного горизонта; 2) обрезка полученного куба до цилиндра с диаметром в 2 см, соответствующего диаметру трубки, в которую в дальнейшем помещался образец; 3) перенос цилиндра почвы в трубку; 4) обрезка нижней части цилиндра. Сразу же после пробоотбора каждый цилиндр был закрыт полиэтиленовой пленкой для предотвращения испарения влаги и сохранения полевой влажности. Все образцы были упакованы в холодильную камеру, в которой поддерживалась температура в 4 °С.

В дополнительно отобранных средних нарушенных образцах почвы с тех же глубин были определены базовые характеристики почвы (табл. 1) (Fomin et al., 2021). Гранулометрический состав почвы был определен методом лазерной дифракции на дифрактометре Microtrac BlueWave (USA) при пробоподготовке с использованием ультразвуковой диспергации с энергией 450 Дж·мл-1 (Юдина, Фомин, 2023; Yudina et al., 2018). Содержа- ние органического углерода (Corg) почвы было определено методом сухого сжигания. Плотность почвы (ρb) была определена буровым методом (Вадюнина, Корчагина, 1961). Пористость почвы (ε) была рассчитана на основании плотности почвы и плотности твердой фазы (Шеин, 2005). Влажность почвы была определена сушкой при 105 °С на протяжении 8 часов (Вадюнина, Корчагина, 1961).

Таблица 1. Характеристики исследуемых образцов

Table 1. Characteristics of studied samples

н я о м S а о U	х© в4 ч ? S 8 1-Н V ^^	о “l ^ it в s	о о ГЧ X© в	ел и		W
AUrz	7.71	83.82	8.47	5.70±0.15	1.01±0.03	60.41±1.04
AU	7.47	84.45	8.08	4.29±0.21	1.12±0.09	55.94±3.43
BCA	8.11	83.82	8.07	3.55±0.22	1.21±0.05	52.65±1.91

Дизайн лабораторного эксперимента по иссушению образца почвы

Схема эксперимента детально описана в работе Fomin et al. (2023). Кратко: насыщение от полевой влажности до полного насыщения (pF = 0) капиллярным поднятием осуществлялось на протяжении двух недель. Дальнейшее иссушение осуществлялось тензиостатическим методом. Равновесие в каждой точке достигалось на протяжении 14–21 дн. Для доведения до абсолютно сухого состояния образцы почв высушивались при 105 °С в течение 48 часов. Соответствующие экспериментальные точки pF – W были использованы для дальнейшей аппроксимации и получения кривых основных гидрофизических характеристик по уравнению ван Генухтена и расчету коэффициента влагопроводности по уравнению ван Генухтена-Муалема.

Томография почв, обработка изображений

Компьютерная томография образцов проведена на томографе SkyScan 1172 (Bruker, Бельгия) с ускоряющим напряжением 70 кВ и силой тока 130 мА. Разрешение полученных изображений размерами 2 000 × 2 000 мкм по осям X и Y соответственно, составляло 7.92 мкм на воксель. Пример полученного 3D-изображения приведен на рисунке 2.

После томографии была произведена реконструкция изображений. Реконструкция осуществлялась с использованием программного обеспечения nRecon (Bruker) со следующими параметрами: сглаживание (гауссово размытие) = 2, усиление пучка = 30%, гистограмма оттенков серого от -500 до 3 000 единиц Ха-усенфилда, где -500 соответствует сигналу ниже сигнала воздуха вокруг образца.

Последующая обработка изображений включала в себя фильтрацию и сегментацию (бинаризацию). Первый этап – фильтрация – необходим для очистки изображения от лишних шумов. Этот шаг был осуществлен при помощи метода нелокальных средних (Buades, Coll, Morel, 2011). Параметры фильтрации: радиус поиска = 10, количество итераций = 4.

Второй этап – сегментация – подразумевает разделение исходного изображения на фазы, в данном случае – на твердую фазу и поровое пространство. Сегментация была выполнена методом наращивания регионов (Hashemi et al., 2014). Границы фаз подбирались визуально, посредством итеративного перебора, параметр pve радиус = 2. Пример 2D-изображения на каждом из этапов обработки приведен на рисунке 1.

Аппроксимация основной гидрофизической характеристики уравнением ван Генухтена

Для построения кривых основных гидрофизических характеристик, экспериментальные точки были аппроксимированы уравнением ван Генухтена (1):

(a)                                        (b)                                          (c)

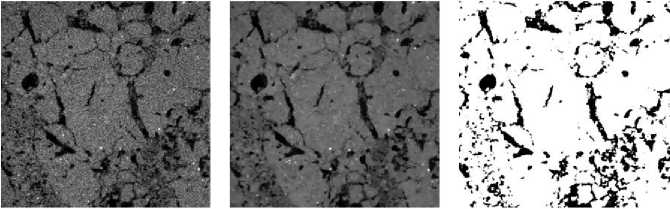
Рис 1. Последовательность шагов в подготовке изображений компьютерных томограмм почв к анализу на примере 2D-изображений каждого этапа обработки. Здесь (a) – исходное изображение, (b) – изображение после фильтрации методом нелокальных средних, (c) – сегментированное на две фазы изображение (черное – поры, белое – твердая фаза).

Fig. 1. Sequence of steps in preparing images of soil computer tomograms for analysis using the example of 2D images of each processing stage. Here ( a ) is the original image, ( b ) is the image after filtering by the non-local means method, ( c ) is the image segmented into two phases (black is pores, white is solid phase).

> .

9- 9 _r _ /     1      \^1-1/n

9 _S - 9 _r = (1 + (a * P)ⁿ⁾

где Se – влагонасыщенность почвы, θ – объемная влажность почвы , θ r – остаточная влажность , θ s – влажность насыщения, α – величина, обратная давлению входа воздуха, P – давление, n – величина, зависящая от пористости почвы (van Genuchten, 1980).

Аппроксимация кривых была выполнена при помощи использования открытой библиотеки SciPy на языке программирования Python 3.12. Полученные после аппроксимации параметры θ r, θ r, α и n были использованы для получения коэффициентов вла-гопроводности по уравнению ван Генухтена-Муалема (2):

m ²

^ вл = K * *S^l _e

,

где K вл – коэффициент влагопроводности почвы, K ф – коэффициент фильтрации почвы и l – параметр, зависящий от связности пор и, как правило, принимаемый равным 0.5 (Mualem, 1976).

Для каждого горизонта значения Se , полученные из уравнения ван Генухтена, были нормализованы на пористость почвы с целью получить значения относительной влагонасыщенности. Значения K вл были нормализованы на значения K ф с целью получить относительную ненасыщенную гидравлическую проводимость. В таких координатах приведены графики основных гидрофизических характеристик и относительных проводимостей.

Извлечение поросетевой модели, моделирование двухфазной проницаемости

Извлечение ПСМ из сегментированных томографических изображений почвы осуществлялось при помощи метода, основанного на дискретной теории Морса, позволяющего сохранять геометрию и топологию порового пространства (Zubov et al., 2022). Для извлечения модели из каждого образца использовалось 3D-изображение размером 1 4003 вокселей. В ПСМ пространство почвы представляется в виде графа, где поры – вершины этого графа, а каналы, связывающие эти поры – грани графа. При извлечении модели сложные формы пор упрощаются до элементарных геометрических фигур: прямоугольника, круга или треугольника. Подобное упрощение производится на основании шейп-фактора поры. Формула и объяснение принципа шейп-фактора приведена в работе Karsanina et al. (2015).

Экстракция ПСМ была выполнена с использованием следующих параметров: предел размера упрощения – 0.0, предел устойчивости упрощения – 1.0, коэффициент заполнения каналов – 0.33. Предел размера упрощения ограничивает максимальный объем поры, которая может участвовать в упрощении. При нулевом значении предел упрощения фактически снимается. Предел устойчи- вости упрощения ограничивает процесс упрощения пределом устойчивости. Чем выше этот предел, тем большее упрощение происходит. Коэффициент заполнения каналов задает часть расстояния между порами, которая будет передана каналам. Для реальных пористых сред используется стандартное значение равное 0.33.

После извлечения модель сохраняется в виде ненаправленного графа в формате “statoil” с сохранением всей геометрической информации. Шейп-факторы для каждой поры также сохраняются. Подробная информация о работе этого формата приведена в работе Gerke et al. (2020). Используя этот формат, ПСМ может быть представлена в виде диаграммы “шаров и цилиндров”, где шары – поры, а цилиндры – каналы между порами. Важно отметить, что данная схема является всего лишь удобным инструментом визуализации: в дальнейшем моделировании проницаемости учитывается форма поры, в то время как на диаграмме все поры выглядят сферически, что не так (рис. 2). Все визуализации ПСМ были созданы с использованием открытой библиотеки vtk .

После извлечения ПСМ они были использованы для моделирования двухфазного течения. Базой такого моделирования является модель Хагена-Пуазёйля для гидравлической проводимости между двумя порами (3):

d el _л q = т-Др, ^L el

где q – поток между двумя порами, соединенными каналом, g el – проводимость флюида в элементе ПСМ длины L el и Δp – давление между центрами пор.

В качестве закона сохранения используется уравнение неразрывности для несжимаемой жидкости (4):

Ь, = 0.

где мы суммируем потоки по у-ым каналам, связывающим i -ые поры.

Рис. 2. Пример поросетевой модели, извлекаемой из 3D-изображения почвы. Здесь ( а ) – 3D изображение почвы, ( b ) – диаграмма “шаров и цилиндров” поросетевой модели.

Fig. 2. An example of a soil pore-network model extracted from a 3D soil image. Here ( a ) is a 3D soil image, ( b ) is a “balls and cylinders” diagram of the soil network model.

Расчет гидравлической проводимости для любого двумерного поперечного сечения (или менисков жидкости для многофазного потока) д основан на безразмерной модели проводимости (Patzek, Silin, 2001) (5):

_ л²д ^д~   V f ’

где А - площадь поперечного сечения, д - безразмерная гидравлическая проводимость, согласно модели “круг-треугольник-квадрат” (Patzek, Silin, 2001), а g - вязкость жидкости.

После того, как все топологические и геометрические свойства порового пространства установлены, проницаемость ПСМ вычисляется путем решения системы линейных уравнений, полученных из уравнений непрерывности (уравнение 4) и импульса, т. е. потока с использованием уравнения Хагена-Пуазёйля (уравене-ние 3) для каждой поры. Задавая давление на входе и выходе, мы можем сначала установить давление в каждой поре, а затем вы- числить коэффициент фильтрации внутри каждого элемента “по-ра-канал-пора” в соответствии с законом Дарси (Valvante, Blunt, 2004).

После определения абсолютной проницаемости (коэффициента фильтрации) мы переходим к моделированию двухфазной проницаемости. Поскольку мы пытаемся симулировать лабораторные эксперименты, в которых из капиллярно-насыщенной почвы тем или иным методом извлекается вода, то в начале симуляции мы считаем все поры заполненными водой. Предполагая, что твердая фаза почвы смачивается водой (угол контакта ниже 90°), мы постепенно наращиваем давление воздуха и проверяем возможность проникновения воздуха в заполненные водой поры и каналы. Таким образом мы, по сути, моделируем классический процесс дренажа. На этом этапе мы проверяем только одно: может ли происходить вытеснение поршневого типа (широко известного в зарубежной литературе как piston-type displacement) при увеличении капиллярного давления, где воздух сначала проникает в самую большую связанную основу пор. Возникновение piston-type displacement устанавливается энергетическим балансом и для круглых пор задается известным уравнением Юнга-Лапласа; для квадратных и треугольных пор его можно вычислить аналитически с использованием метода, описанного в Ma et al. (1996). Затем давление входа воздуха вычисляется как (Øren et al., 1998):

p .   -

1 entry

a c osyres(1 + 2YnG)

r

F d (Y re _S 'G)

P _d (O re _S ,G}

1+ 11+^^-

^ COS²e _r

(1+2jnG) '

где Fd - безразмерный поправочный коэффициент для смачивающей жидкости, которая может удерживаться в углах, о - поверхностное натяжение между воздухом и водой; γres – контактный угол, .D-сложная функция межфазного интерфейса мениска и локальных углов поперечного сечения (Ma et al., 1996); г - радиус поры или канала, G – шейп-фактор поры. После входа воздуха в поровое пространство локальные положения менисков можно вычислить в соответствии с Рentry. Если геометрия менисков в попе- речном сечении известна, можно определить гидравлическую проводимость для фаз воздуха и воды в данной поре (Patzek, Kristensen, 2001). Таким образом, задавая шаги давления, мы вычисляем положения менисков на каждом из шагов давления. Когда увеличение давления воздуха не приводит к дальнейшему изменению водонасыщенности, процесс дренажа останавливается. Как правило, следующим этапом идет моделирование пропитки образца, однако в данной работе такое моделирование не осуществлялось, и потому его подробное описание не приводится. На рисунке 3 приведено схематичное изображение процесса дренажа в треугольной поре.

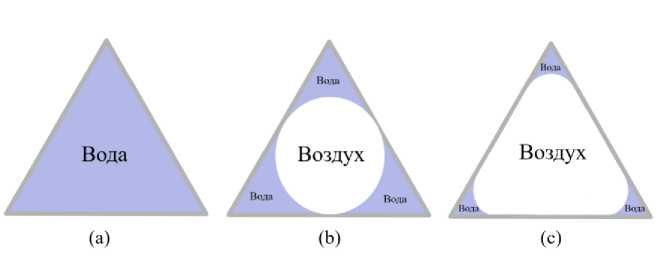
Рис. 3. Схематичный пример моделирования двухфазной проницаемости в поросетевой модели при дренаже в треугольной поре-канале треугольного сечения. Здесь ( а ) – пора целиком заполнена водой, ( b ) – воздух входит в пору, вода остается в менисках, ( с ) – дренаж продолжается, водные мениски утончаются. Направление потока от себя. Fig. 3. Schematic example of modeling two-phase permeability in a porenetwork model with drainage in a triangular pore-throat. Here ( a ) – the pore is completely filled with water, ( b ) – air enters the pore, water remains in the meniscus, ( c ) – drainage continues, water meniscus becomes thinner.

После определения положений менисков на каждом шаге капиллярного давления мы вычисляем водонасыщенность в системе и относительные проводимости воды и воздуха по уравнениям 3 и 4, что позволяет нам получить ненасыщенную гидравли- ческую и пневматическую проводимости. Основные гидрофизические характеристики в данном методе получаются построением зависимости водонасыщенности на каждом конкретном шаге давления.

Моделирование однофазного и двухфазного течений в масштабе пор было осуществлено посредством открытой библиотеки pnflow (Valvante, Blunt, 2004). Характеристики флюида для воды и воздуха были зафиксированы для комнатной температуры (20 °C), и во время моделирования предполагались идеальные условия смачивания водой (краевой угол смачивания равен 0°). Поток моделировался вдоль направления Z.

Помимо исследования гидрофизических свойств почвы, ПСМ также может быть применена для количественного анализа порового пространства. Используя извлеченные ПСМ, были оценены общее количество пор и каналов, а также распространенные (Tolstygin et al., 2025; Gerke et al., 2024) в исследовании пористых сред параметры – эйлерова характеристика и связность. Эйлерова характеристика определялась как разность между количеством пор и каналов, связность – среднее количество каналов на пору. Эти параметры используются для сравнения поведения пористого пространства в разных образцах: уменьшение числа пор и увеличение числа каналов приводят к росту связности и уменьшению эйлеровой характеристики образца, что позволяет делать выводы об изменении физических свойств порового пространства.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Извлечение поросетевой модели

Из каждого исследованного 3D-изображения компьютерной томографии почв была извлечена поросетевая модель. Все поросетевые модели были визуализированы для оценки качества извлечения и соответствия исходной 3D-структуре (рис. 4).

Из извлеченных ПСМ были получены количественные характеристики – число пор, число каналов, эйлерова характеристика и связность (табл. 2). Согласно полученным данным, количество пор снижается от горизонта AUrz к горизонту AU и вновь возрастает к горизонту BCA. Прямо противоположное происходит с количеством каналов. Как следствие, такое поведение приводит к уменьшению эйлеровой характеристики и росту связности в горизонте AU.

Радиус пор.

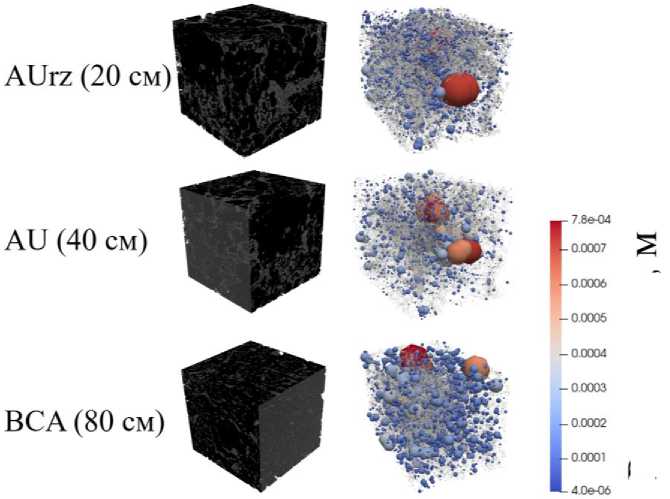
Рис. 4 . Результаты извлечения поросетевой модели. Здесь слева – 3D-изображение образца почвы, справа – извлеченная поросетевая модель.

Fig. 4. Results of the extraction of the pore network model. Here on the left is a 3D image of the soil sample, on the right is the extracted pore network model.

Таблица 2. Характеристики извлеченных поросетевых моделей

Table 2. Characteristics of the extracted network models

Горизонт	Число пор	Число каналов	Эйлерова характеристика	Связность
AUrz	180379	66831	113548	0.741
AU	173209	83619	89590	0.966
BCA	180658	58036	122622	0.642

Моделирование двухфазной проницаемости

Посредством моделирования двухфазной проницаемости в ПСМ были получены кривые иссушения (дренажа) для каждого исследованного образца. Модельные кривые сравнивались с кривыми, полученными аппроксимацией уравнением ван Генухтена экспериментальных точек основной гидрофизической характеристики (рис. 5). В каждом из исследованных горизонтов наблюдаются схожие закономерности при сравнении поведения кривых, полученных аппроксимацией уравнением ван Генухтена и моделированием в масштабе пор в ПСМ – расхождение и образование двух зон дивергенции в областях низкой (0 <  S w < 0.4) и высокой (0.8 <  S w < 1) водонасыщенности. Уравнение ван Генухтена показывает адекватную степень аппроксимации, однако расходится с экспериментальными показаниями в областях высокого давления.

На основе ПСМ исследуемых образцов были получены кривые зависимости ненасыщенной гидравлической проводимости (коэффициентов влагопроводности, нормированных на коэффициент фильтрации – насыщенную гидравлическую проводимость) от относительной влагонасыщенности почвы. Модельные кривые сравнивались с кривыми, полученными расчетом по уравнению ван Генухтена-Муалема с использованием параметров аппроксимации экспериментальных точек основной гидрофизической характеристики уравнением ван Генухтена (рис. 6). Коэффициент l в уравнении ван Генухтена-Муалема принят равным 0.5.

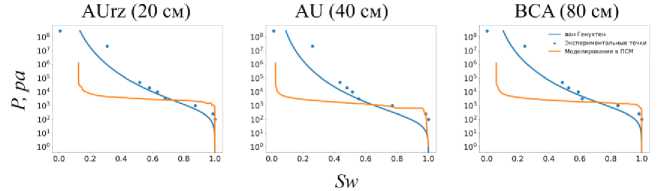
Рис. 5. Основные гидрофизические характеристики, полученные аппроксимацией экспериментальных точек уравнением ван Генухтена и полученные моделированием двухфазной проницаемости в поросетевой модели. Ось абсцисс отложена в S w – относительной влагонасыщенности почвы. Важно отметить, что ось ординат соответствует отрицательному давлению, но для удобства просмотра отражена как положительная.

Fig. 5. The main hydrophysical characteristics obtained by approximating the experimental points with the van Genuchten equation and obtained by modeling two-phase permeability in a pore-net model. The X-axis is plotted in S w – the relative moisture saturation of the soil. It is important to note that the Y-axis corresponds to negative pressure, but for ease of viewing is reflected as positive.

AUrz (20 см)          AU (40 см)            ВСА (80 см)

Sw

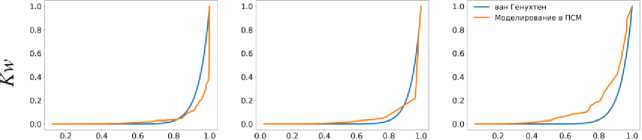
Рис. 6. Относительные ненасыщенные гидравлические проводимости, рассчитанные по уравнению ван Генухтена-Муалема и полученные моделированием двухфазной проницаемости в поросетевой модели. Ось абсцисс отложена в S w – относительной влагонасыщенности почвы. Ось ординат отложена в K w – относительной ненасыщенной гидравлической проводимости.

Fig. 6. Relative unsaturated hydraulic conductivities calculated using the van Genuchten-Mualem equation and obtained by modeling two-phase permeability in a pore network model. The X-axis is S w – the relative soil moisture saturation. The Y-axis is K w – the relative unsaturated hydraulic conductivity.

Кривые, полученные по уравнению ван Генухтена-Муалема и моделированием в ПСМ хорошо сходятся в горизонте AU. В горизонте AUrz кривая, полученная моделированием в ПСМ, лежит чуть ниже кривой ван Генухтена-Муалема, а в горизонте BCA – чуть выше. В горизонтах AUrz и BCA, где кривые не сходятся, аналогичным образом можно добиться большей сходимости результатов, варьируя параметр l , однако это не является темой данного исследования.

Распределение пор по размерам

Для количественной оценки порового пространства были получены кумулятивные кривые распределения пор по размерам, полученные из основных гидрофизических характеристик для аппроксимации по уравнению ван Генухтена и из моделирования в ПСМ (рис. 7). Максимальным достижимым значением пористости считается наибольшая объемная влажность, нормированная на пористость образца. Полученный результат позволяет интерпретировать появление двух зон дивергенции на кривых водоудержи-вания (рис. 8).

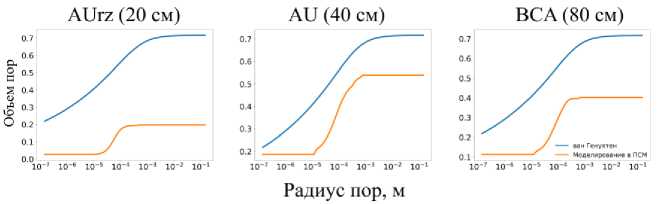
Рис. 7. Кумулятивные кривые распределения пор по размерам, полученные из основных гидрофизических характеристик для аппроксимации по уравнению ван Генухтена и из моделирования в поросетевой модели.

Fig. 7. Cumulative pore size distribution curves obtained from the main hydrophysical characteristics for approximation using the van Genuchten equation and from modeling in the pore network model.

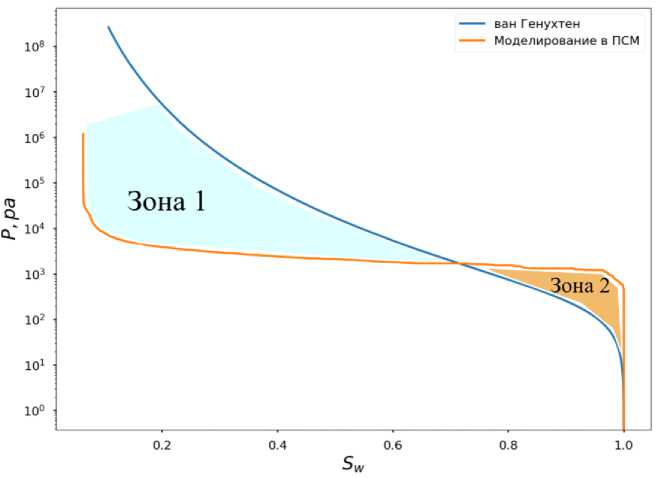
Рис. 8. Две зоны дивергенции в основных гидрофизических характеристиках, полученных аппроксимацией уравнением ван Генухтена и моделированием в поросетевой модели. Важно отметить, что ось ординат соответствует отрицательному давлению, но для удобства просмотра отражена как положительная.

Fig. 8. Two zones of divergence in the main hydrophysical characteristics obtained by approximation with the van Genuchten equation and modeling in the pore-network model. It is important to note that the Y-axis corresponds to negative pressure, but for ease of viewing is reflected as positive.

На графиках видно, что в областях пор среднего размера (10-5–10-3 м) поведение кумулятивных кривых, полученных моделированием в ПСМ, фактически повторяет поведение кривых, полученных из основных гидрофизических характеристик по уравнению ван Генухтена. В областях микропористости (10-7–10-5 м) и макропористости (10-3–10-1м) видно “платообразное” поведение кривых: то есть общий объем порового пространства не увеличивается за счет вклада этих пор – они фактически отсутствуют в образце. Причинами такого “отсутствия” являются ограничение разрешения томографии (в области микропор) и наличие граничных эффектов (макропористость), суть которых раскрывается в следующем параграфе.

Сравнение результатов, полученных моделированием в поросетевой модели и методом ван Генухтена

Полученные результаты для образцов из различных горизонтов почвы демонстрируют одинаковую закономерность. Аппроксимация уравнением ван Генухтена практически идеально ложится на экспериментальные точки. Исключение составляют точки высоких значений pF , что, впрочем, неоднократно подтверждалось в других исследованиях (Ghanbarian-Alavijeh et al., 2010). Тем не менее, интересным является наличие двух областей дивергенции между экспериментальными данными и моделированием в ПСМ (рис. 8). Появление зоны 1 обуславливается несовершенством метода компьютерной томографии в силу недостаточности максимальной детализации почвы. На томографических изображениях и в полученных ПСМ нет части микропористости за пределами разрешения съемки (<7.92 мкм), которая присутствует в образце, и которую мы можем оценить через весовую пористость. Этот результат сходится с данными, полученными в исследовании Gerke et al. (2024), где в качестве исходных образцов также были выбраны черноземные почвы, а концепция “недостатка” микропор в ПСМ была подтверждена экспериментально.

Зона 2 отображает гораздо более низкие измеренные капиллярные входные давления и значения давления в целом для насыщений между 1.0 > Sw > 0.8. Причина отклонения между измеренными и модельными данными связана с граничными условиями лабораторного эксперимента – любой образец почвы будет обладать некоторой неоднородностью там, где он отделен от остальной почвы. Во время насыщения образца некоторые локальные области на поверхности образца будут заполняться водой и дренироваться при гораздо более низких капиллярных давлениях по сравнению с почвой, погруженной в ту же пористую среду вокруг нее. Такие искусственно большие поры могут возникать не только наверху или внизу образца, но и близко к стенкам цилиндрического образца из-за ориентации частиц (Khirevich et al., 2007). Эта проблема известна в нефтяной инженерии, где часть капиллярной кривой, близкая к Sw = 1, обычно рассматривается как ненадежная (Jennings, 1987).

Результаты исследований по сравнению измеренной и смоделированной ненасыщенной гидравлической проводимости показывают противоречивые результаты. В нашей работе сравнение ненасыщенной гидравлической проводимости показывает, что моделирование в ПСМ позволяет получить достаточно близкие результаты к измеренным значениям (рис. 7). Полученные в данной работе результаты подчеркивают хорошую сходимость моделирования в ПСМ с классическими подходами физики почв. Однако в смежной работе авторы наблюдали сильную дивергенцию, обуславливаемую нефизичностью параметра связности пор l в уравнении ван Генухтена-Муалема (Gerke et al., 2024). Сложности в воспроизводимости сходимости результатов прямых измерений и моделирования требуют проведения дальнейших исследований на более широком фактическом материале, включая образцы разного структурного генезиса.

Анализ пригодности применения поросетевых моделей

Результаты работы позволяют сделать утверждение, основанное на ряде критериев, о том, что моделирование гидродинамических свойств почвы с применением ПСМ является крайне перспективным подходом и значительно более надежно, чем классический подход ван Генухтена.

Первый критерий – временные затраты для получения данных. Несмотря на то, что обработка данных и дальнейшие расчеты коэффициента влагопроводности довольно просты, получение экспериментальных измерений основной гидрофизической характеристики почв занимает несколько месяцев (Fomin et al., 2023). Моделирование в ПСМ занимает порядка 4–8 часов на компьютерную томографию образца и порядка 2–4 часов на последующее извлечение ПСМ и дальнейшее моделирование в масштабе пор. Прочие подходы к получению экспериментальных данных ОГХ

(центрифугирование, тензиометрия и т. п.) приводят к разной степени изменения структуры почвы перед или во время анализа, что не отражает реального пространственного поведения потоков (Schlüter et al., 2016).

Второй критерий – широкие возможности математического моделирования. Моделирование в ПСМ позволяет проводить виртуальные эксперименты, например, получение кривых пропитки образцов для изучения гистерезиса основной гидрофизической характеристики и симуляции движения влаги при различных условиях смачивания твердой фазы (Bentz et al., 2022). Подобные исследования крайне трудно провести в лабораторных условиях. Несмотря на то, что в данной работе подобные исследования не проводились, они были подсвечены в других работах (Gerke et al., 2024). Таким образом, ПСМ открывают доступ к более корректной оценке гидрологического режима почв.

Третий критерий – решение проблемы “граничных пор” (рис. 8) с помощью моделирования в ПСМ при измерениях гидродинамических свойств почв. Отметим, что учет “граничных пор” особенно важен для верхних слоев почвы (в том числе пахотных), где наличие таких пор может сильно влиять на правильную оценку верхних граничных условий инфильтрации влаги. ПСМ позволяют учитывать любые типы граничных условий, в том числе с крупными порами на границах или, что особенно важно, при окружении образца почвы остальным почвенным пространством. Таким образом, моделирование в ПСМ в дальнейшем может быть использовано для моделирования гидродинамических свойств на уровне почвенного профиля и ландшафта вместо прямых измерений.

Поросетевое моделирование предлагает новый концептуальный подход в понимании структуры порового пространства. Классический подход ван Генухтена-Муалема основан на капиллярной модели представления пор и предлагает использование коэффициента l в качестве параметра связности пор. В оригинальной работе значение параметра предлагается принимать равным 0.5. Позднее было показано (Дедюлина и др., 2014), что значение этого параметра необходимо варьировать для получения адекватных значений коэффициента влагопроводности, в том числе, в об- ласть отрицательных значений, что противоречит физике процесса. Парадигма представления порового пространства исключительно в виде капилляров не раз подвергалась критике (Fan, 1956; Dullien, 2012; Hunt el al., 2013). В критических работах подчеркивается несоответствие реальной геометрии и топологии порового пространства, из которого проистекают заведомо некорректные представления о течении гидродинамических процессов. Поросетевое моделирование, в свою очередь, разрешает эти проблемы.

Несмотря на достоинства ПСМ, имеется ряд важных недостатков, подчеркнутых в том числе и в этой работе, которые необходимо упомянуть. Первым из таких является нехватка максимального разрешения компьютерной томографии. Многие исследователи (Karsanina et al., 2018; Wu et al., 2019; Li et al., 2020) сходятся во мнении, что проблема может быть решена методами повышения пространственного разрешения томографических изображений, включая super-resolution (Bai et al., 2023) и multi-scale image pore structure fusion (Karsanina et al., 2018; Wu et al., 2019; Li et al., 2020, Gerke et al., 2017). Другой проблемой является невозможность определить остаточную влажность θr. Поскольку лабораторный эксперимент осуществлялся на тензиостате, точные значения θr не могли быть достигнуты. Фактически вся оставшаяся в ПСМ на конец дренажа вода удерживается там из-за капиллярных эффектов. В некоторых исследованиях удалось учесть известные значения θr в ПСМ (Valvatne, Blunt, 2004).

Важным допущением гидродинамического моделирования с использованием ПСМ является предположение о несжимаемости твердой фазы почвы, что определенно не является идеальным приближением ненасыщенных условий потока в почвах. Другая актуальная проблема, которая требует доработки в текущей реализации ПСМ, – регулирование растворения воздуха в воде и учет ненасыщенной пневматической проводимости.

ВЫВОДЫ

В работе было осуществлено моделирование в поросетевой модели на 3D-изображениях компьютерной томографии образцов разных горизонтов миграционно-мицеллярного чернозема Курской области и сравнение результатов этого моделирования с классическими подходами физики почв. Результаты сравнения позволяют сделать вывод о перспективности применения ПСМ в почвоведении, поскольку они обладают следующими преимуществами:

• -    скорость моделирования;

• -    близкие значения коэффициентов влагопроводности с измеренными в сравнении с расчетами по уравнению ван Генух-тена-Муалема;

• -   решение проблемы граничных эффектов;

• -   возможность учета гистерезиса;

  -   возможность учета различных краевых углов смачивания.

Тем не менее, остается ряд вопросов, ответы на которые будут найдены в ходе проведения дальнейших исследований по данной тематике:

- Каким образом на поведение основных гидрофизических характеристик будут влиять начальные условия влажности в образце?

- Как будут отличаться гидродинамические свойства почв при изменении структуры образца? Проведенный в (Fomin et al., 2023) эксперимент позволил установить, что структура порового пространства является крайне динамичной, что должно влиять на свойства поросетевых моделей, основанных на одном и том же образце в его разных состояниях?

- Каким образом применение поросетевых моделей может повлиять на устоявшиеся методологии определения почвенногидрологических констант? Может ли поросетевое моделирование стать заменой/усовершенствованием педотранс-ферных функций?

- Наконец, насколько более точно будут оценены гидродинамические свойства почвы при применении поросетевых моделей и как это повлияет на их практическое применение: оценку поливных норм, запасов влаги и так далее?