Анализ и расчет непуассоновских моделей трафика в сетях ЭВМ

С развитием высокоскоростных сетей связи, все большее влияние на качество обслуживании оказывает т.н. свойство самоподобия потоков. С практической точки зрения это можно объяснить высокой изменчивостью интенсивности трафика и, как следствие, высокой пачечностью поступления пакетов в узел сети при высокой скорости передачи данных, что приводит, из-за ограниченности буфера, к потерям пакетов. Расчеты времен задержки, объемов буфера по классическим методикам приводят к слишком оптимистическим результатам [1-3]. Для того, чтобы обеспечить заданное качество обслуживания, необходимо более детально анализировать самоподобные потоки с целью их прогнозирования и определения их характеристик для возможного динамического управления трафиком в современных сетях связи. Кроме того, новые возможности сервиса обслуживания (Grade of service – GoS), к примеру, подавление пауз в голосовом трафике (VAD – Voice Activiti Detection) усложняют динамику трафика и требуют пересмотра традиционной теории те- летрафика и массового обслуживания, которые не учитывают свойств непуассоновских потоков.

За последнее десятилетие появилось достаточное количество работ в области исследования самоподобных процессов, большинство из которых посвящены их теоретическому анализу через автокорреляцию с вычислением коэффициента Херста (Hurst). Однако среди них совсем мало работ для практического расчета показателей производительности сетевых структур при наличии такого трафика из-за отсутствия математического и программного инструментария для этого. Разумно организованная сеть должна обеспечивать низкий процент блокировок и высокую загрузку каналов связи. Сюда необходимо также добавить ограничения сверху на величину задержки или на ее вариацию (джиттер). Все это требует разработки и теоретического обоснования методов анализа и прогнозирования трафика с тяжело-хвостными распределениями для последующего динамического управления им.

Распределения с тяжелыми хвостами

Современные средства исследования локальных (LAN) и глобальных (WAN) сетей позволяют получать данные наблюдений по трафику за достаточно длинный отрезок времени и проследить долговременную зависимость, т.е. процесс самоподобия, если он имеет место. Далее будем рассматривать самоподобные процессы как потоки событий с распределениями интервалов времени с тяжелыми хвостами. Считается, что случайная величина имеет распределение с тяжелым (весомым) хвостом (РТХ или Heavy Tailed), если:

1 - F (т) ~ x “ при x ^да ,            (1)

то есть функция распределения затухает по степенному закону в отличие от экспоненциаль -убывания хвоста распределения.

Тогда распределение с тяжелым хвостом имеет следующее свойство:

lim e ^{2 x} (1 - F ( x )) = 0, VT >  0 (2) x →∞

Среди функций распределений с тяжелым хвостом будем рассматривать подкласс так называемых субэкспоненциальных распределений с коэффициентом вариации cv > 1, куда можно отнести распределения Вейбулла, гамма, логнормальное и гиперэкспоненциальное. Эти распределения удовлетворяют условиям (1)-(2). На рис. 1-2 приведены графики функций плотности перечисленных выше распределений в сравнении с экспоненциальным законом распределения.

На рис.2 те же графики приведены в логарифмическом масштабе.Нарис.1-2,дляприведенных распределений Вейбулла, гамма, логнормального игиперэкспоненциального,соответственно,сред-ние значения и дисперсии есть m _T = D _T = 0,25 , что дает коэффициент вариации распределения cv = 2,0.

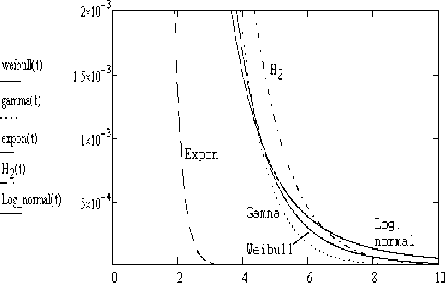
Рис. 1. Графики функций плотности в обычном масштабе

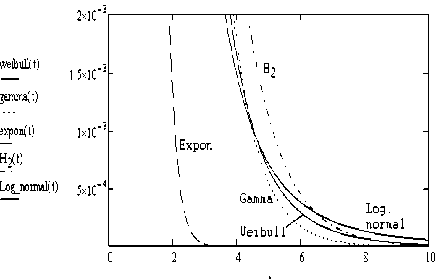
Рис. 2. Графики функций распределений в логарифмическом масштабе

Таким образом, рассмотрим подкласс субэкспоненциальных распределений с одинаковыми средними и дисперсиями распределений интервалов времени между событиями. Как известно, коэффициент вариации экспоненциального закона равен 1.

Как видно из этих графиков, даже при сравнительно небольшом коэффициенте вариации распределения cv = 2,0 , заметна тяжесть хвостов затухания приведенных выше функций плотностей по сравнению с экспонентой. Очевидно, что с увеличением параметра cv весомость хвоста распределения только возрастет.

Постановка задачи

Трафик в современных сетях с коммутацией пакетов, как IP-телефонии так и корпоративных сетях с магистральными каналами передачи данных, принято считать самоподобным [1-3]. Степень самоподобия классически измеряют с помощью параметра Херста H, который для временного ряда X_k ( k = 1; 2 … N ) определяют из статистики соотношения

R/S = (a N ) H , (3)

где R = max( X _k ) - min( X _k ) - размах отклонения NT!

временного ряда, S =       £ (X^ - X) ² -

N — 1 к = 1

исправленное среднее квадратическое отклоне- ние, N - число членов ряда, а = const.

По показателю параметра H , выделяют три типа случайных процессов:

• -    0 <  H < 0,5 – случайный процесс являет-

• ся антиперсистентным, или эргодическим рядом, который не обладает самоподобием;

• -    H = 0,5 – полностью случайный ряд, аналогичный случайным смещениям частицы при классическом броуновском движении;

• -    H > 0,5 – персистентный (самоподдержива-ющийся) процесс, который обладает длительной памятью и является самоподобным.

В данной работе для анализа и расчета характеристик самоподобного трафика предлагается использовать разработанный авторами математический и программный инструментарий, основанный наметодедвумернойдиффузионнойаппроксимации процессов функционирования СМО типа GI/G/k/m [4-5] и программы имитации таких систем [6].

Для этого проведем моделирование работы каналов сетей передачи данных как систем массового обслуживания (СМО) GI/G/k/m с целью определения основных характеристик сети,таких как загрузка канала передачи данных, задержка,время отклика пользовательских приложений и вероятности потерь пакетов. В качестве законов распределений интервалов времени поступления и обслуживания будем рассматривать распределения с тяжелыми хвостами. Оценим также степень отличия полученных результатов от результатов применения классических моделей в виде пуассоновских входных потоков и экспоненциально распределенных временах обслуживания.

Решение задачи

Для оценки основных показателей производительности сетевых структур будем использовать известные результаты двумерного диффузионного приближения СМО GI/G/k/m имитационного моделирования по программной системе авторов [6] и классические результаты для СМО M/M/1, M/G/1 .

Для этого рассмотрим одно из приведенных выше распределений - гамма-распределение и покажем, что коэффициент Херста,вычисленный для трафика, образованного случайным процессом с законом распределения гамма,будет выше 0,5.Тогда такой процесс можно считать самоподобным.Сле-довательно,можно будет выдвинуть предположение о том, что,если коэффициент вариации определенного закона распределения больше 1 ( cv >  1), то и коэффициент Херста H процесса с таким законом распределения, выше 0,5.

Ниже на рис. 3-6 приведены графики случайного процесса с гамма-распределением со средним и дисперсией m _T = D _T = 0,25. Таким образом, коэффициент вариации такого распределения cv = 2.

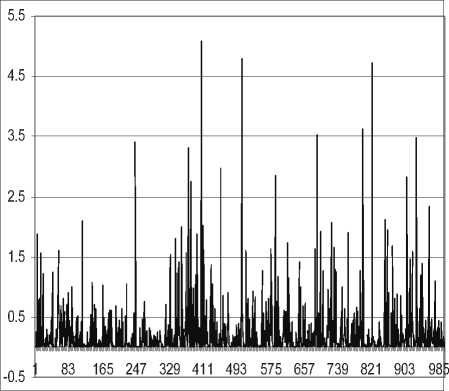
Рис. 3. Число отсчетов процесса N = 1000

Из рис.3-6 видно,что рассматриваемый случай-ныйпроцесс при укрупнениивременных интервалов, сохраняет свои характеристики,то есть он самоподо-бен.Дальнейшие расчеты по определению коэффи- циента Херста из соотношения (3)показывают (см. рис.7),что он равен 0,56.Тем самым предположение о том,что если коэффициент вариации определенного закона распределения больше 1 (cv > 1) ,то и коэффициент Херста H с таким законом распределения, выше 0,5 полностью подтверждается.

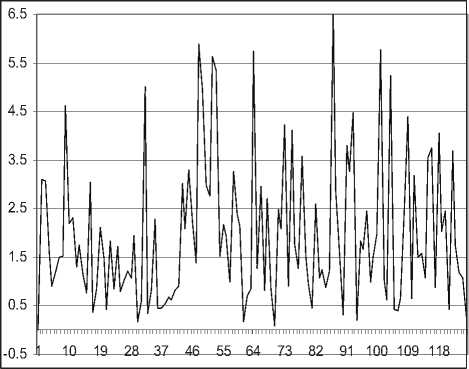
Рис. 4. Число отсчетов процесса N = 500

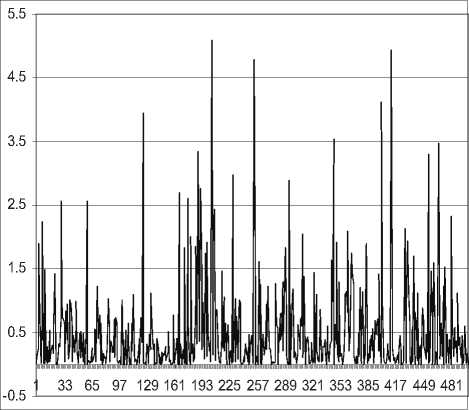
Рис. 5. Число отсчетов процесса N = 250

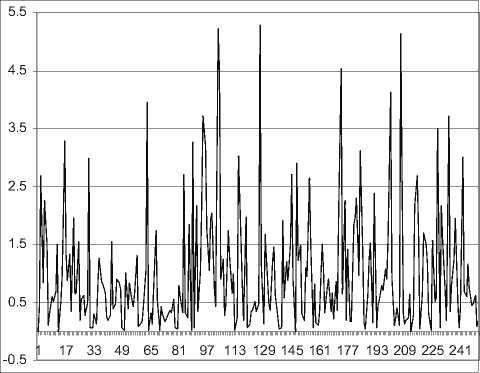
Рис. 6. Число отсчетов процесса N = 125

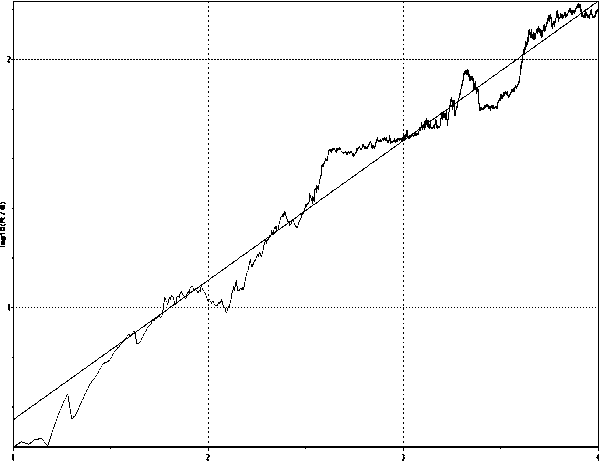
Рис. 7. Зависимость lg( R/S ) от lg N

В таблицах 1-3 приведены результаты моделирования каналов связи в виде различных

Таблица 1

систем массового обслуживания при диапазоне изменения коэффициента загрузки от 0,1 до 0,95. При этом определялась основная характеристика системы – среднее время ожидания требования в системе W в зависимости от загрузки ρ. Среднее время обслуживания во всех расчетах принято за 1, то есть использовано нормированное время обслуживания. Здесь использованы следующие сокращения: M/M/ 1 – система с пуассоновским входным потоком и с экспоненциальным временем обслуживания; GI/M /1 – система с произвольным рекуррентным входным потоком и с экспоненциальным временем обслуживания; M/G /1 – система с пуассоновским входным потоком и произвольно распределенным временем обслуживания; ДДА – метод двумерной диффузионной аппроксимации СМО.

	Среднее время ожидания W для системы GI/M/ 1
Загрузка ρ	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95
СМО M / M /1	0,11	0,25	0,43	0,67	1,0	1,5	2,33	4,0	9,0	19,0
Метод ДДА	0,28	0,68	1,29	1,89	2,55	3,93	6,08	10,32	22,93	48,0
Результаты имитационного моделирования Гамма-распределение	0,29	0,64	1,10	1,67	2,54	3,76	5,82	10,01	22,35	46,25
Результаты имитационного моделирования Распределение Вейбулла	0,28	0,63	1,08	1,67	2,51	3,77	5,87	10,29	23,27	47,34

Таблица 2

	Среднее время ожидания W для системы M/G/ 1
Загрузка ρ	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95
СМО M / M /1	0,11	0,25	0,43	0,67	1,0	1,5	2,33	4,0	9,0	19,0
Формула Полячека-Хинчина	0,28	0,63	1,07	1,67	2,50	3,75	5,83	10,0	22,50	47,50
Метод ДДА	0,24	0,63	1,05	1,63	2,45	3,68	5,76	9,94	22,47	47,52
Результаты имитационного моделирования Гамма - распределение	0,39	0,89	1,35	1,97	2,79	4,67	6,82	11,12	23,34	46,77
Результаты имитационного моделирования Распределение Вейбулла	0,49	0,89	1,35	1,96	2,79	4,03	6,08	10,37	22,75	51,32

Таблица 3

	Среднее время ожидания W для системы GI/G/ 1
Загрузка ρ	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95
СМО M / M /1	0,11	0,25	0,43	0,67	1,0	1,5	2,33	4,0	9,0	19,0
Формула Полячека-Хинчина	0,28	0,63	1,07	1,67	2,50	3,75	5,83	10,0	22,50	47,50
Метод ДДА	0,63	1,42	2,50	4,03	5,95	6,48	9,89	16,63	36,66	76,67
Результаты имитационного моделирования Гамма-распределение	1,14	1,82	2,63	3,66	5,02	7,04	10,32	17,19	36,28	78,05
Результаты имитационного моделирования Распределение Вейбулла	0,78	1,42	2,18	3,19	4,53	6,56	9,88	16,94	37,35	81,86

Из таблицы 1 видно, что если входной трафик распределен по закону гамма или Вейбулла с характеристиками mT = DT = 0,25 (коэффициент вариации распределения cv = 2,0), то значения для среднего времени ожидания W отличаются от результатов классической модели M/M/1 примерно в 2,5 раза в большую сторону. Следовательно, классическая модель с пуассоновским входным потоком и экспоненциальным временем обслуживания сильно недооценивает среднее время ожидания требования в очереди в случае самоподобного трафика. Примерно такая же картина наблюдается в том случае, если рассматривать случай пуассоновского входного трафика и времени обслуживания с распределением с весомым хвостом (см. таблицу 2). Результаты таблицы 3 показывают, насколько ухудшаются харак- теристики системы в том случае, когда и входной поток и время обслуживания имеют распределения с весомым хвостом.

Теперь рассмотрим поведение другой важной характеристики системы – вероятности потери пакетов P _отк в случае конечного объема канального буфера. Для этого в таблице 4 приведены расчеты этого показателя для разных моделей систем: M/M/ 1; GI/M/ 1; M/G/ 1; GI/G/ 1 в зависимости от загрузки ρ и объема буфера m . Для определенности рассмотрен случай объема канального буфера m = 2. Результаты вычислительных экспериментов, приведенные в таблице 4 также показывают, что классическая пуассоновская модель трафика сильно недооценивает вероятность потерь пакетов в случае распределений с весомым хвостом.

Таблица 4

	Вероятность потери требования Pотк (объем буфера m = 2)
Загрузка ρ	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95
СМО M / M /1 формула Эрланга	0,005	0,016	0,033	0,054	0,077	0,101	0,126	0,151	0,176	0,188
Результаты имитационного моделирования GI / M /1	0,121	0,161	0,190	0,211	0,230	0,246	0,260	0,271	0,282	0,287
Результаты имитационного моделирования M / G /1	0,122	0,163	0,194	0,212	0,231	0,248	0,263	0,272	0,284	0,288

Заключение

За последнее десятилетие появилось достаточное количество работ в области исследования самоподобных процессов как моделей сетевого трафика, большинство которых посвящены их теоретическому анализу через автокорреляцию с вычислением коэффициента Херста. Однако среди них мало работ, посвященных практическому расчету показателей производительности сетевых структур при наличии такого трафика из-за отсутствия математического и программного инструментария для этого. В данной работе для анализа и расчета характеристик непуассоновских моделей трафика предлагается использовать разработанный авторами математический и программный инструментарий, основанный на методе двумерной диффузионной аппроксимации процессов функционирования СМО типа GI/G/k/m [4-5] и программной системы имитации таких систем [6].

Вычислительные эксперименты, проведенные с использованием предлагаемого инструментария, напрямую подтверждают тот факт, что пуассоновские модели сетевого трафика обеспе- чивают слишком оптимистические показатели производительности сетевых структур, недооценивая как задержки пакетов, так и вероятности их потерь. По мнению авторов, предлагаемый инструментарий и полученные результаты могут быть интересны специалистам, которые занимаются вопросами теории телетрафика и самоподобных процессов.