Анализ и расчет процесса низконапорного обратного осмоса при регенерации санитарно-гигиенической воды

На перспективных космических станциях и планетных базах планируется организация замкнутого контура санитарногигиенического водообеспечения с регенерацией воды. Ранее авторами предложены метод и принципиальная схема регенерации санитарно-гигиенической воды (СГВ), и проведена оценка затрат массы при введении на борт МКС различного набора средств санитарно-гигиенического обеспечения совместно с системой регенерации СГВ [1]. В настоящей статье обосновывается и предлагается метод инженерного расчета обратноосмотического модуля — основного аппарата системы регенерации воды.

В системе регенерации санитарногигиенической воды предполагается применение низконапорного обратного осмоса (рабочий перепад давления составляет 0,7–1,3 МПа), который представляет наибольший интерес с точки зрения энергозатрат и безопасности. При проведении санитарно-гигиенических процедур на борту предусматривается возможность использования общепринятых моющих средств (МС). Экспериментальные исследования проводились при использовании жидкого МС «Адажио».

Для реализации в системе регенерации процесса очистки с высоким коэффициентом извлечения чистой воды выбрана схема тангенциальной фильтрации в рулонном обратноосмотическом модуле с концентрированием МС и загрязнений в циркуляционном контуре с емкостью постоянного объема. Такая схема позволяет получить высокий коэффициент извлечения воды [2, 3]. Эксперименты на рулонных обратноосмотических модулях марки NanoRO с мембраной РМ33К показали, что при концентрировании МС от 2 до 250 г/л при рабочем давлении процесса 0,2…0,8 МПа возможно достижение степени извлечения чистой воды 0,97–0,98. При этом селективность мембраны по моющему средству превысила 98% [4]. Следует отметить, что при опреснении морской воды степень извлечения не превышает 0,30 [5]. При этом процесс обратноосмотической очистки смесей сложного состава типа МС имеет ряд особенностей, которые необходимо учитывать при разработке методики расчета обратноосмотической аппаратуры.

физическая картина процесса обратноосмотической очистки

Обратный осмос — это мембранный процесс разделения, движущей силой которого является перепад давления. Поток воды через мембрану описывается следующим уравнением [4, 6, 7]:

j = K ₁( ∆ P – ∆π ) = K ₁ ∆ P _эф, (1) где j — поток воды через единицу площади мембраны; K ₁ — коэффициент проницаемости по воде для мембраны; ∆ Р _эф = ( ∆ Р – ∆π ) — эффективная разность давлений между напорным каналом и каналом фильтрата; ∆ Р — разность давлений в напорном канале и канале фильтрата; ∆π — разность осмотических давлений исходного раствора в напорном канале и фильтрата (пермеата). Коэффициент пропорциональности K ₁ аналогичен используемому в уравнении Хагена – Пуазейля, зависит от свойств мембраны и обратно пропорционален вязкости жидкости.

Согласно уравнению (1), для осуществления процесса обратноосмотической очистки необходимо создать рабочее давление в напорном канале аппарата, которое будет превышать осмотическое давление разделяемого раствора. При установившемся процессе (рис. 1, рассмотрена двухкомпонентная смесь) поперечный поток отбираемого через мембрану компонента в напорном канале обусловлен эффективным перепадом давления через мембрану. Вместе с потоком отбираемого компонента к мембране переносится и пассивный компонент, который задерживается мембраной. У поверхности мембраны образуется концентрационный пограничный слой, в пределах которого наблюдаются рост концентрации не проходящих через мембрану компонентов раствора и снижение эффективного перепада давления. Эффект концентрационной поляризации компенсируется диффузионно-конвективным отводом этих веществ в ядро потока.

Предполагается, что константа проницаемости мембраны по воде K1 известна (имеется в литературе или определена экспериментально). Так как селективность мембраны по МС близка к 100%, рассматриваем массоперенос только в канале очищаемой жидкости. Неизвестным для расчета по уравнению (1) является значение осмотического давления МС у поверхности мембраны, определяемое его концентрацией W2гр.

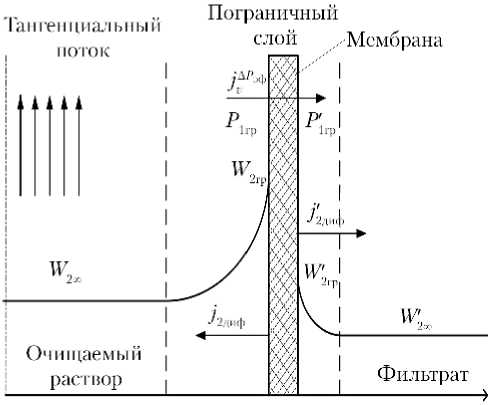
Рис. 1. Физическая картина массопереноса в напорном канале мембранного аппарата: j_v ^{∆ Pэф} — поперечный поток отбираемого компонента в напорном канале мембранного аппарата за счет перепада давления ∆ Р_эф; j_2диф и j₂ ′ _диф — диффузионный молекулярно-конвективный поток растворенного вещества от поверхности мембраны в канале исходного раствора и канале фильтрата, соответственно; W_{2 ∞} , W₂ ′_∞ — относительная массовая концентрация растворенного вещества (пассивного компонента) в ядре потока исходного раствора и фильтрате, соответственно; W ,  W ′    — относительная массо-

2гр 2гр вая концентрация растворенного вещества (пассивного компонента) у границы мембраны в канале исходного раствора и канале фильтрата, соответственно; P = Р – π , P′ = Р – π′ ; пунктир обозначает 1гр рабоч гр 1гр фильтрата гр условную границу диффузионного пограничного слоя; индексом ∞ обозначена среда вне пограничного слоя; 1 — вода (активный компонент, проходящий через мембрану); 2 — моющее средство (пассивный компонент, не проходящий через мембрану)

Поперечный поток отбираемого компонента через мембрану из напорного канала мембранного аппарата, вызванный перепадом давления, вносит в пограничный слой количество МС j_v ^{∆ P эф} W _{2 ∞} . При установившемся процессе такое же количество МС должно отводиться от поверхности мембраны за счет диффузии:

^j v ^{∆ P эф W} 2∞ ^{= j} 2диф ^.

Для расчета j _2диф используем общепринятое соотношение для конвективного массообмена (2) с использованием коэффициента массоотдачи β :

j 2диф = ρβ ( W 2гр – W 2∞ ). (2)

Связь осмотического давления π с концентрацией выражает модифицированное уравнение Вант-Гоффа [8]:

n ρ

π = RT (i k W), k=1 Mk k где π — осмотическое давление раствора; i = 1 + α′ — коэффициент Вант-Гоффа; α′ — степень диссоциации растворенного вещества; R — универсальная газовая постоянная; Т — абсолютная температура раствора; W — относительная массовая концентрация; ρ — плотность; M — молекулярная масса; π(NaCl) = 0,84С; π(МС) = 0,032С — аппроксимированные зависимости, используемые для практических расчетов, где С — концентрация в г/л.

канала; D — коэффициент диффузии растворенного вещества; ρ∞, ρгр — плотности разделяемого раствора в ядре потока и на границе раздела фаз.

Принципиальным моментом является

βd использование [9, 10] Nu* = э W2гр — диф- фузионного числа Нуссельта, построенного по молекулярной составляющей потока массы, что учитывает отличие граничных условий массо- и теплообмена и фактора проницаемости (числа Сполдинга), приведенного к соотношению концентраций:

Применение расширенной аналогии между массо- и теплообменом для определения коэффициента массоотдачи

В связи с недостатком данных для расчета часто возникают трудности при определении коэффициента массоотда-чи. Многие авторы [9–12] теоретически и экспериментально рассматривали влияние поперечного потока (вдув и отсос) на коэффициент массоотдачи β . В случае обратного осмоса для расчета β целесообразно использовать теорию расширенной аналогии между массо- и теплообменом [9, 10] с использованием имеющихся в литературе критериальных уравнений подобия для теплообмена. Данная теория уже успешно применяется для расчета тепломассообменной аппаратуры, в которой осуществляются фазовые переходы [13], но не нашла еще широкого применения для расчета аппаратуры обратноосмотической очистки.

Уравнение подобия для массоотдачи записывается в следующем виде [10]:

W 1гр – W 1∞

1 – W ^. 1гр

Для описания функций f ₁ и f ₂ целесообразно использовать соотношения, предложенные в литературе [11, 12]:

f ₁ ( B ) =

^{1 + B – 1 2}

0,5 B      ^;

^f 2

^{ρ ∞} ρ _гр

1 +

^ρ∞ ^0,5

ρ гр

Обработка экспериментальных данных по очистке от МС показала, что в нашем случае f ₁( B ) → 1 и f ₂( ρ_∞ / ρ _гр) → 1, т. е. справедлива аналогия Колборна:

.                      ( Pr

Nu D * = Nu D 0 W 2гр = Nu 0 ^Pr r _D

n

W . 2гр

β d                 ρ

Nu D = Nu D * 2гр = WW 2гр = Nu D, f 1 ( ^B) f, p=- f 3 (Le). D                      гр

β d _э где Nu _D = _D ^э

диффузионное число Нус-

Здесь Nu _{D 0} определяется критериальными уравнениями для теплообмена без массообмена с заменой числа Pr на число Pr _D (Sc). Оценка влияния значительного отличия чисел Pr и Pr _D и большой величины числа Le являются задачей дальнейших исследований.

аппараты с рулонными модулями

сельта (число Шервуда Sh), построенное по общему потоку массы; Nu _{D 0} — диффузионное число Нуссельта при очень малом потоке массы растворенного компонента ( j → 0, B → 1); W _2гр — относительная массовая концентрация пассивного компонента (в нашем случае — МС)

у границы мембраны; L_e     ^D — число

Pr

Льюиса; d _э — эквивалентный диаметр

Аппараты с рулонными модулями (рис. 2) являются одними из наиболее распространенных, конструктивно наиболее удачных для осуществления процесса обратного осмоса и применяются при проведении экспериментальных исследований. В то же время аппараты такого типа являются наиболее сложными для расчета. Толщина длинных спиральных напорных каналов в рулонных модулях не превышает 1 мм, при этом отношение эквивалентного диаметра канала к его длине неизвестно, так как по длине напорного канала имеются разделяющие сетки. Это делает сечение переменным, перемешивает поток и снижает влияние концентрационной поляризации. Проведение расчета таких аппаратов затруднительно. В связи с этим требуются новые подходы к расчету аппаратов с модулями рулонного типа.

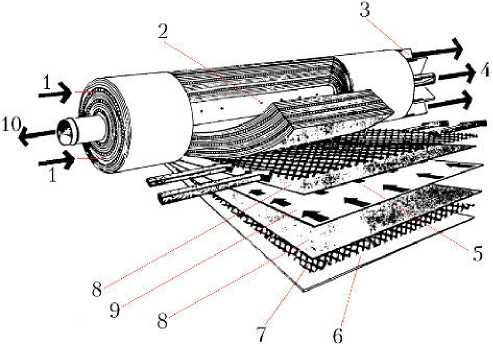
Рис. 2. Строение рулонного обратноосмотического модуля [14, 15]: 1 — исходный раствор; 2 — трубка; 3 — анти-телескопическое устройство; 4 — выход сконцентрированного исходного раствора; 5 — направление движения пермеата (фильтрата); 6 — оболочка; 7 — сетка-турбулизатор; 8 — мембрана; 9 — дренаж; 10 — выход пермеата (фильтрата)