Анализ и разработка математических методов и моделей для совершенствования технологических процессов испытаний изделий

кой модели управления. Учитывая изложенное и, исходя из объема первого этапа внедрения в управление испытаниями СВТ, выделим объекты моделирования в пространстве . Для этого ограничимся агрегатами: насосной станцией и стендом ресурсных испытаний подъемников.

Далее эти два объекта выделим во времени . Период моделирования во времени должен совпадать с расчетным интервалом времени, на котором задан критерий управления. Для оборудования непрерывного действия – это, как правило, межремонтный срок (межрегламентный период); для оборудования периодического действия – длительность рабочего цикла.

Работу гидравлической насосной станции можем отнести к оборудованию непрерывного действия, поэтому математическая модель контроля работы станции должна охватывать период между двумя очередными обслуживаниями станции.

Математическая модель стенда ресурсных испытаний подъемников по времени должна охватывать период времени выполнения одного блока испытаний, то есть время выполнения 9375 циклов функционирования и повторно -статических нагружений.

Выделение объекта моделирования в пространстве координат его проведения тесно связано с выбранной целью управления, так как из всей совокупности входных воздействий, влияющих на ход процесса, и входных переменных, характеризующих протекание процесса, необходимо выбрать те величины, которые будут изменяться при решении задачи исследования или управления [2]. К этим величинам относятся управляющие воздействия u ₁ , u ₂ ,... u _n , которые являются целенаправленно изменяемыми в процессе управления входными воздействиями, и управляемые переменные

X₁,X ₂,... X m , относящиеся к тем выходным переменным, информация об изменении которых используется для формирования управляющих воздействий. Остальные входные воздействия z ₁, z ₂,... z l следует отнести к возмущающим , а выходные переменные к неуправляемым. Возмущающие воздействия следует классифицировать как внешние , связанные с подачей энергии, и внутренние , связанные с состоянием оборудования. При составлении математической модели рекомендуется использовать преимущественно векторную форму записи:

^x = X 1 , X 2 , L X n ¹

y = {y 1, y 2,l y„ 1

^z = { z 1 , z 2 , L Z n } •

Для исследования процессов управления существует большое количество методов создания математических моделей описывающих работу тех или иных технических систем. В исследованиях процессов управления испытаниями оценим возможность использования трех из них.

Метод конечных элементов (МКЭ) – численный метод получения приближенных решений для широкого круга инженерных задач [95]. В настоящее время он распространился на решение задач механики сплошных сред. Приложение МКЭ может быть разделено на три категории в зависимости от природы решаемой задачи.

К первой категории относятся задачи, известные как задачи равновесия, независящие от времени. При решении этих задач необходимо найти распределение температур, давлений и скорости в механике потоков.

Ко второй категории относятся задачи собственных значений механики твердого тела и потоков. Это задачи, не зависящие от времени, при решении которых определяются значения собственных частот и форм колебаний твердых тел и потоков. Примерами этих задач могут являться такие как определение условий устойчивости конструкций и ламинарных потоков, а так же колебаний жидкости в упругих базах.

К третьей категории относятся задачи зависимые от времени. Обычно эти задачи формулируются из задач первых двух категорий, когда они начинают зависеть от времени.

МКЭ применим почти в каждой отрасли техники, но это не означает, что этот метод является наилучшим именно для этой модели. В континуальных задачах поле переменных (давление, температура, перемещение, напряжение и другие параметры) принимает бесконечное множество значений, поскольку это есть функция отдельной точки системы (тела). Следовательно, такие задачи имеют бесконечное множество не- известных. Для сведения к конечному числу неизвестных рассматриваемую область (систему) разбивают на элементы и выражают неизвестное поле внутри каждого элемента через аппроксимирующие функции. Аппроксимирующие функции определяют через значения поля переменных в отдельных точках, которые называют узлами элементов. Узлы обычно выбирают на границах элементов. Кроме наружных узлов могут быть и внутренние узлы, которые лежат внутри элемента. Узловые точки и аппроксимирующие функции полностью определяют поле переменных внутри элемента. Результаты решения и степень погрешности зависят от числа и размеров используемых элементов, а так же от выбранных аппроксимирующих функций. Эти функции нельзя выбирать произвольно, так как они должны удовлетворять условиям совместимости.

Точность, с которой множество отдельных частей описывают целое, обычно зависит от числа, размеров и типа элементов.

Началом составления математической модели по МКЭ является дискретизация какой-либо системы, то есть замены реальной системы идеализированной системой, состоящей из отдельных элементов, которые соединяются друг с другом в отдельных точках, называемых узлами. В примере гидравлической насосной станции можно гидравлическую систему разделить на составные части: гидробак, фильтр, гидравлический насос, радиатор охлаждения, магистрали между вентилями и гидравлическими редукторами.

Рассмотрим гидравлическую систему, представленную на рис. 1.

Гидравлическая система состоит из нескольких пересекающихся ветвей. Необходимо найти давление и расход исходящий как из насоса, так и в каждом элементе этой системы.

Разобьем систему трубопроводов на конечные элементы. Как видно из рис. 1 идеальная система состоит из 15 узлов и 20 элементов. Выделим отдельно элемент (рис. 2).

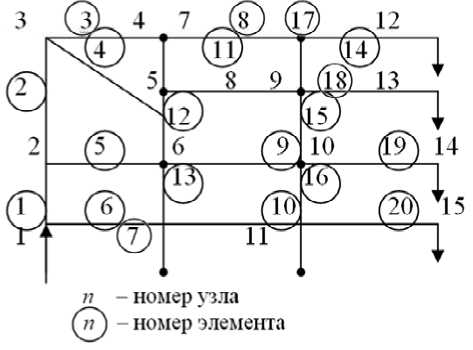
Рис. 1. Гидравлическая схема

L

Q

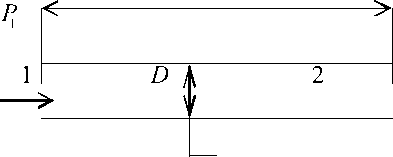
Рис. 2. Элемент гидравлической системы

Зависимость перепада давлений Р и расхода Q описывается законами гидравлики. Если предположить что поток ламинарный, то перепад давлений между узлами 1 и 2 можно получить через выражение:

128 QT

Р-Р =-

P1 P 2            ,

nD

где L –длина трубы, Q – расход жидкости, D – диаметр трубы, Ц - динамическая вязкость жидкости.

Выражая потоки для каждого узла можно записать:

Q = 1^ P ^- p 2 ) •        (2)

Q 2 = n D P 2 ^- p > .         (3)

В матричной форме:

n D ⁴ f 1 ¹⁸² L L^{- 1}

- 4! рЦ Q I ¹Л P ₂J Q J

или \Лр ^] ' ^{P }} " ^{ Q ^} , (4) где \Л p ] — матрица текучести;

{ P } - вектор узловых давлений;

{ Q } — вектор узловых потоков.

Эти матричные уравнения представляют математическую модель элемента гидравлической системы. Потери давления на вентилях не учитываются. Обычно их учитывают введением в систему исполнительных труб с эквивалентной длиной. Рассмотренные уравнения справедливы только для ламинарного потока. Задачи с турбулентным потоком становятся нелинейными и для изучения этих процессов применяются другие законы гидравлики.

Математическая модель всей приведенной гидравлической системы будет представлять совокупность матричных уравнений являющихся моделями отдельных участков гидравлической системы.

Вариационный метод – основан на применении вариационного исчисления для создания математических моделей. Вариационное исчисле- ние занимается задачей отыскания наибольших и наименьших значений функционалов, определенных на множестве линий и поверхностей. То есть экстремальными значениями, где исследование экстремумов проводят методом вариаций малого возмущения аргументов и функционалов. Задачи, относящиеся к вариационному исчислению, в этом смысле, являются конкурирующими дискретным задачам оптимизации. Весьма широкий круг задач описывает следующая схема. Требуется минимизировать функционал:

x 2

J ( Y ( x )) = J F ( x , y , y ' ) dx , x 1

где F ( x , y , y ') некоторая известная функция трех переменных в классе С (класс допустимых функций или функций сравнения).

Пусть Е – класс функций сравнения функционала J . Функционал J имеет в этом классе относительный минимум (максимум), реализуемый функцией y ( x ) е E , если для любой функции y ( x ) е E выполняется неравенство J ⁽ y ^{( x} )) ^ J ⁽ y ^{( x} )) [ J ( y ( x )) ^ J ( y ( x )) ] • ^то ^^сть приращение функционала А / = J ( y ( x )) - J ( y ( x )) неотрицательно (неположительно). Если функция y = y ( x ) , принадлежащая к классу функций сравнения, удовлетворяет граничным условиям и реализует экстремум функционала, то она является решением уравнения (уравнения Эйлера):

F y — dx^F y = ⁰. (5)

Данное уравнение определяет математическую модель процесса описываемого с помощью математической теории оптимального управления.

Метод моделей аппаратов. Аппараты – самые простые среди объектов управления технологическими процессами. Структура и вид модели аппарата зависят от характера исходной информации об объекте управления, цикличности его режимов работы и назначения модели [2]. Для определения характера цикличности работы во временном интервале функционирования разрабатываемой модели выделяют время t _непр непрерывного протекания процесса и время t _пер осуществления периодического процесса. Цикличность работы технологического оборудования характеризуется с помощью коэффициента периодичности:

п =

t пер

t +t пер непр

по значению которого технологические аппараты на принятом временном интервале разделяют на аппараты непрерывного ( п = 0 ) • полунепрерывного ( 0 <  п <  1 ) , и периодического ( п = 1 ) действия.

Если целью управления аппаратом непрерывного действия (АНД) является стабилизация технологических режимов в соответствии с технологическим регламентом, то для разработки соответствующих систем управления используют наиболее полные модели управляемых объектов, в которых учитываются динамика, нелинейность, возмущающие воздействия. Если возникает задача оптимизации таких объектов, то при значительной размерности модели ее упрощают, используя статические, а в некоторых случаях и линеаризованные модели при условии, что их точность будет не ниже требуемой.

Математическая модель аппаратов периодического действия (АПД) имеет логико–динамическую структуру. В общем виде она может быть представлена системой выражений: