Анализ и синтез адаптивного фрикционного контакта твердых тел с косвенным регулированием

УДК 621.838.222                                         

В работе [1] исследован модифицированный вариант адаптивного фрикционного контакта (АФК) первого поколения, который теоретически позволяет сохранить постоянство сил трения между фрикционными парами при колебаниях величины коэффициента трения. Принципиальным отличием этого АФК является введение упругой связи между чувствительными элементами (ЭЧ), а также профилирование рабочих поверхностей гнезд под ЭЧ специальной кривой линией, благодаря чему управляющее воздействие изменяется по заданному закону в зависимости от текущего коэффициента трения при постоянном сдвигающем усилии.

Недостаток указанного АФК, заключающийся в низкой нагрузочной способности, объясняется тем, что задающее и управляющее воздействия имеют на выходе сумматора разные знаки. Соответственно этому назначение приведенного коэффициента трения по величине исходного коэффициента трения, большей минимального значения, приводит к исчезновению управляющего воздействия внутри интервала изменения возмущающего воздействия.

Ранее предложены структурно-функциональная и синтезированная на ее основе принципиальная схемы АФК твердых тел, в которых для полной стабилизации силы трения в условиях изменения величины коэффициента трения используется положительная обратная связь. Это позволяет значительно повысить нагрузочную способность АФК.

Однако, эффективность использования задающего воздействия в АФК не исследована и не приняты меры по ее повышению. Кроме того, не найдены условия эффективного функционирования системы автоматического регулирования АФК в интервале изменения возмущающего воздействия.

ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ

Синтез положительной обратной связи и исследование ее эффективности в синтезированном АФК твердых тел.

ОСНОВНАЯ ЧАСТЬ

Проблема создания АФК, лишенного указанного недостатка, заключается в том, чтобы решить две следующие задачи:

• 1.    Построение структурно-функциональной и на ее основе принципиальной схемы АФК, в котором подаются на вход сумматора задающее и управляющее воздействия одного знака. Это позволяет производить настройку АФК по максимальному значению коэффициента трения и сохранить управляющее воздействие во всех режимах работы АФК.

• 2.    На основе анализа созданных схем АФК установить закономерность формирования управляющего воздействия в функции возмущающего воздействия и определить параметры управляющего устройства.

Для обеспечения одинаковых знаков задающего и возмущающего воздействий, поступающих на вход сумматора, ЭЧ должны быть расположены по отношению к последнему с той же стороны, что и нажимной узел. Если использовать традиционное представление о сумматоре, которым является нажимная планка [2–4], то ЭЧ может располагаться либо между сумматором и нажимным узлом, либо последний – между сумматором и ЭЧ, причем нажимной элемент должен быть подвижен в осевом направлении относительно нажимного диска. Поскольку данный способ регулирования предполагает изменение осевой деформации упругого элемента нажимного узла, его минимальная деформация будет соответствовать работе АФК с максимальным коэффициентом трения, а также его статическому состоянию. Тогда в случае уменьшения коэффициента трения снизится сила трения АФК, поэтому из-за малого управляющего воздействия саморегулирование становится невозможным. Следовательно, изменение осевой деформации упругого элемента при саморегулировании АФК должно предполагать дополнительное воздействие на упругий элемент.

Этому условию удовлетворяет АФК, структурно-функциональная схема, которая приведена на рисунке 1. Как и в базовом варианте, сигнал pFT с выхода АФК поступает на чувствительные элементы 1 датчика-преобразователя 2, а выходной сигнал ЭЧ – управляющее воздействие FР на сумматор 3 датчика-преобразователя. Сумматор не является частью фрикционной группы 4 и не связан с нею непосредственно. Выходной сигнал ЭЧ поступает на вход сумматора, имея тот же знак, что и сигнал упругого элемента 5, в результате чего на вход фрикционной группы поступает трансформированный сигнал FП ± cxi (FП – усилие упругого элемента 5 при fi = fmax , c и xi – осевая жесткость и текущая осевая деформация упругого элемента). Дополнительное силовое воздействие на сумматор 3 нажимного узла 6 осуществляется упругим элементом 7 дополнительного нажимного узла 8 с переменным выходным сигналом FП1 ± c1 xi (FП1 – усилие упругого элемента 7 при значении fi = fmax , c1 – осевая жесткость упругого элемента). Поскольку сумматор не представляет собой составную часть фрикционной группы, последний относится к контакту с так называемым косвенным регулированием.

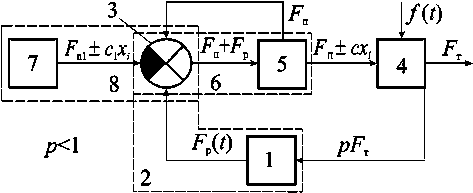
• 1    – чувствительные элементы;

• 2    – датчик-преобразователь; 3 – сумматор;

• 4    – фрикционная группа; 5 – упругий элемент;

6 – нажимной узел; 7 – упругий элемент

• 1    – sensitive elements; 2 – sensor-converter; 3 – adder;

• 4    – the friction group; 5 – elastic element;

• 6    – pressure assembly; 7 – elastic element

Рисунок 1 – Структурно-функциональная схема АФК

Figure 1 – Structural and functional diagram of the adaptive friction contact

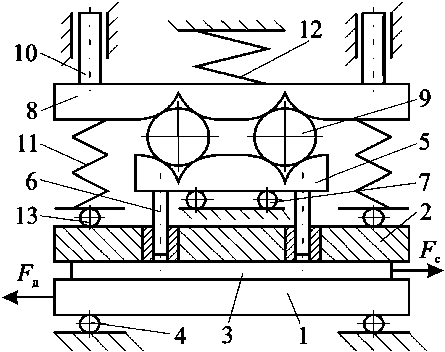
Эквивалентная принципиальная схема АФК изображена на рисунок 2. Тела 1 – 3 , образующие фрикционную группу, опираются на неподвижную поверхность с помощью катков 4 и прижаты друг к другу посредством пружин 11 , которые вместе с планкой 8 , являющейся сумматором, представляют нажимной узел. Планка 8 несет штоки 10 , размещенные в линейных направляющих, и поджата в направлении фрикционной группы пружиной 12 , которая вместе с сумматором составляет дополнительный нажимной узел. Между планками 5 и 8 размещены в профилированных гнездах чувствительные элементы в виде роликов 9 . Планка 5 опирается на неподвижную поверхность с помощью катков 7 и несет штоки 6 , входящие в направляющие каналы тела 2 . Для уменьшения трения между опорными концами пружин 11 и телом 2 установлены опоры качения 13 . Планки 5 , 8 и ролики 9 составляют датчик-преобразователь.

1–3 – тела, образующие фрикционную группу;

• 4    – каток; 5 – планка; 6 – шток; 7 – каток;

8 – планка; 9 – ролик; 10 – шток; 11 – пружина;

12 – пружина; 13 – опора качения

1-3 – bodies forming the friction group; 4 – roller;

• 5    – bar; 6 – rod; 7 – roller; 8 – bar; 9 – roller;

10 – rod; 11 – spring; 12 – spring; 13 – rolling support

Рисунок 2 – Принципиальная схема АФК Figure 2 – Principle diagram of the adaptive friction contact

Настройка АФК, определяемая отношением первоначальных усилий затяжки пружин 11 и 12 ( F_П и F_П1 соответственно), может производиться различными способами. Для упрощения хода рассуждений примем такое соотношение сил F_П и F_П1 , при котором выполняется условие

FП1 - c1 x - (FП + cx) - FP1 + FTP = 0.

Здесь F_Р1 = (F_П + cx) f_min tgα_o – управляющее воздействие при минимальном уровне возмущающего воздействия f_min , α_o – начальный угол давления ЭЧ, F_ТР – сила трения на штоках 10 , x – максимальный вертикальный ход планки 8 при саморегулировании.

Таким образом, при минимальном значении коэффициента трения между телами 1 – 3 и F_Д >  F_С ( F_Д – движущая сила, приложенная к телу 1 , F_С – сила сопротивления, приложенная к телу 3 ) устройство находится в состоянии относительного равновесия, тангенциальное смещение планки 5 отсутствует, и ролики 9 максимально погружены в гнезда.

Если произойдет увеличение коэффициента трения, состояние относительного равновесия элементов АФК будет сохраняться до тех пор, пока FС = const. При возрастании FС в условиях сохранения соотношения FД > FС увеличится тангенциальная сила на роликах 9 и, как следствие, управляющее воздействие FР . Равновесие планки 8 нарушится, и она сместится вверх, в результате чего уменьшится сжатие пружины 11 и прижатие тел 1–3 друг к другу. В этом для рассматриваемой схемы АФК заключается принцип саморегулирования силы трения.

Для установления закономерности изменения F_Р в процессе саморегулирования воспользуемся следующими рассуждениями. Управляющее воздействие изменяется при саморегулировании от нуля (при значении f_i = f_max ) до величины F_Р.max (при значении f_i = f_min ), то есть в обратном направлении по отношению к основной модели АФК первого поколения [5], поэтому запишем

ΣFT.i = 2 (FП + FP.i ) fi , (1)

где Σ F_T.i – суммарная текущая сила трения АФК; F_Р.i – текущее управляющее воздействие; f_i – текущее возмущающее воздействие.

Поскольку рассматривается задача обеспечения постоянства выходного параметра Σ F_T.i при изменении возмущающего воздействия f_i , представим настроечный выходной параметр как

ΣF′T = 2FП fН , (2)

где f_Н – настроечное значение возмущающего воздействия.

На данном этапе исследования величина f_Н является неопределенной, однако, безусловно, она должна принадлежать интервалу значений f_min ... f_max .

Приравняв правые части (1) и (2) и решив полученное уравнение, найдем:

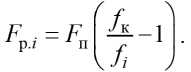
Для того чтобы рассматриваемый фрикционный контакт сохранял адаптивные качества в указанном интервале изменения возмущающего воздействия, управляющее воздействие F_Р.i должно существовать внутри этого интервала и принимать нулевое значение, по крайней мере, на одной из его границ. Нетрудно убедиться, что данным условиям в найденном соотношении полностью удовлетворяет единственное значение f_H = f_max .

Следовательно, исследуемый АФК должен создавать постоянный выходной параметр, равный максимальной величине выходного параметра неадаптивного (то есть имеющего линейную зависимость выходного параметра от возмущающего воздействия) фрикционного контакта, имеющего те же конструктивные основные параметры.

График функции (3) является гиперболой, не имеющей асимптоты и пересекающей ось абсцисс в точке f = fmax.

Поскольку функция (3) не соответствует за- кономерности изменения управляющего воздействия основной модели АФК первого поколения [6], форма образующей рабочей поверхности гнезда под ролики рассматриваемой схемы контакта должна быть другой.

Для отыскания необходимой формы образующей запишем уравнение равновесия сил, действующих на планку 8 нормально к плоскости контакта тел 1 – 3 , для ее произвольного положения

FП + c x - 2c xi + FP.i = FП1 - c1 x + 2c1 xi + FТР . (4)

При составлении уравнения учтено удвоенное вертикальное перемещение планки 8 относительно произвольной фиксированной точки профиля рабочей поверхности гнезда планки 5 .

Уравнение (4) отражает процесс саморегулирования АФК при увеличении f_i . В случае уменьшения f_i знаки перед третьими слагаемыми в обеих частях соотношения (4) и перед последними слагаемыми правой части должны быть заменены на противоположные (рис. 1).

Максимальный ход планки 8 может быть найден из следующего уравнения ее равновесия в крайнем нижнем положении:

FП1 - FП - x (с + с1 ) = 0, откуда определим:

x =

F П1 - F П _{с + с 1}

Здесь принято FР = |FТР| , то есть tgαo = f. Подставив полученное значение в уравнение найдем:

(F П + cx ) f min = F П

f max

FП1 = FП

^{с f} max ^{+ с} 1 ^(f max ^{- f} min ⁾

с f min

Тогда

x

=       f max -f min

П с f min

Принимая во внимание, что

F P.i = F П f max tgα i ,

FТР = FП fmax f1, найдем из уравнения (4):

2 xi

tgαi = f1 + F f (c + c1 ). П max

Поскольку при выводе уравнения (6) в качестве исходного принято положение тел АФК, определяемое значением коэффициента трения f_min , величина x_i = 0 соответствует максимальному погружению роликов 9 в гнезда.

Левая часть (6) представляет собой тангенс угла наклона касательной к образующей рабочей поверхности гнезда, поэтому уравнение образующей найдем интегрированием (6):

с + с1

y = x f1 + F f x2 + C.

П max

Постоянная интегрирования C может быть найдена из начальных условий: y = y_o при x = 0. Тогда C = y_o ( y_o – начальная ордината кривой, очерчивающей профиль гнезда). Она находится аналогично изложенному в работе [1]:

когда сила трения пары 1 – 3 станет равной настроечному выходному параметру контакта (суммарной силе трения), управляющее воздействие (распорная сила на роликах 9 ) обратится в нуль. Если перед увеличением коэффициента трения он был больше минимального значения, планка 8 будет занимать промежуточное положение, и суммарная сила натяжения пружин 11 равна F_П + cx_i . Обращение управляющего воздействия в нуль может привести или не привести (это зависит от соотношения величин F_П , F_П1 , c и c₁ ) к изменению положения планки 8 .

Можно записать

(FП + cxi ) fm = 2FП fmax.

Здесь fm – искомая предельная величина коэффициента трения, при которой исследуемый АФК еще сохраняет адаптивные свойства, то есть способен к автоматическому регулированию [7].

Найдем:

y

o

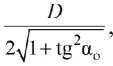
f m

П max

FП +с fmax

где D – диаметр ролика.

Коэффициент рассогласования [1] для рассматриваемого АФК равен:

2 f - f max m = f - f .                   (7)

max

Очевидно, что величина f_m зависит только от перемещения x_i и принимает минимальное значение при условии x_i = x . Очевидно также, что, по меньшей мере, в одном случае – при исходной величине f = f_min – необходимо учитывать указанное значение x . Тогда с учетом соотношения (5) получим

Функция (7) является возрастающей, что свидетельствует о нарастании рассогласования между силами Σ F_T.i и F_Р по мере увеличения f и о более эффективном использовании задающего воздействия F_П для получения необходимого уровня выходного параметра Σ F_T.i . Следовательно, переменная величина коэффициента m характеризует эффективность работы датчика-преобразователя АФК, а соотношение знаков изменения коэффициента рассогласования и коэффициента трения – эффективность использования задающего воздействия.

Базовая модель АФК первого поколения и муфта-аналог [5] имеют ограничение величины параметра управляющего устройства, зависящего от f_max . Несоблюдение этого условия снижает надежность их работы, что обусловлено выключением управляющего устройства при увеличении коэффициента трения до некоторого значения. Рассматриваемый вариант АФК имеет другую форму связи датчика-преобразователя и нажимного узла, поэтому подход к установлению величины внутреннего параметра контакта, который позволяет сохранить его надежную работу в интервале изменения возмущающего воздействия, будет иным.

Если в процессе работы АФК произойдет увеличение коэффициента трения до такой величины,

f m

П max

max min

FП +сx

_f max

= 2 f . min

Как видим, интервал изменения возмущающего воздействия, в котором АФК, имеющий две пары трения фрикционной группы, сохраняет адаптивные свойства, мал: его верхняя граница не покрывает даже среднее значение f [8, 9]. Расширение интервала можно произвести следующим образом: увеличить число фрикционных пар, оставив одну пару ведущей. В этом случае имеем

f m

П max

FП +сx

= z f min

где z – число фрикционных пар контакта.

Очевидно, что верхняя граница интервала изменения возмущающего воздействия должна соответствовать значению f_max , тогда:

f max z = _f min

.

Учитывая полученный результат, можно записать

У = xfi +

c + q

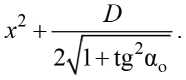
Установленных выше параметров недостаточно для полного синтеза АФК. Действительно, для обеспечения нормальной работы контакта необходимо найти ограничение величины ( tgα ) _max . Отыскание последней представляется особенно важным, так как эта величина должна обеспечивать под действием всех силовых факторов установку элементов АФК в положение, при котором выполняется (10) для любого текущего значения f_i . Кроме того, необходимо определить соотношение некоторых геометрических параметров датчика-преобразователя и величины осевых жесткостей пружин 11 и 12.

Учитывая, что для сохранения адаптивных качеств АФК в интервале значений f_min ... f_max фрикционная группа должна иметь z пар трения, запишем окончательно

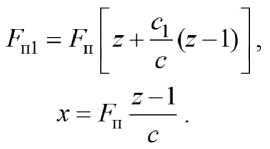
Если условием работоспособности датчика-преобразователя, то есть способностью к саморегулированию, в области малых значений возмущающего воздействия является определенное усилие F_П1 в соответствии с соотношением (8), то при максимальной величине возмущающего воздействия критерием работоспособности служит величина ( tgα ) _max . Действительно, при уменьшении возмущающего воздействия от величины f_min ... f_max должно произойти увеличение силы сжатия пружины 11 за счет изменения соотношения силовых факторов, действующих на планку 8 . Так как перемещению последней вниз противодействует, кроме усилия пружины 11 и силы трения между штоками 10 и направляющими, управляющее воздействие F_Р , возникающее в результате действия силы трения, условием перемещения вниз планки 8 является необходимость тангенциального перемещения планки 5 .

При уменьшении возмущающего воздействия от максимального значения в процессе передачи контактом нагрузки произойдет соответствующее уменьшение силы трения между телами фрикционной группы [10], что приведет к падению величины управляющего воздействия FР , действующего на планку 8. Уменьшение силы трения, в свою очередь, приведет к проскальзыванию фрикционных пар и к смене трения покоя трением скольжения. Особенностью этой ситуации является то, что АФК сразу реагирует на уменьшение возмущающего воздействия, тогда как в противном случае последствия увеличения последнего проявляются только при возрастании нагрузки Fс . Поэтому, приняв в качестве уменьшения величину, равную fmax (1- n) (n = fc.max / fmax, fc.max – максимальный коэффициент трения скольжения, fmax – максимальный коэффициент трения покоя), запишем условие перемещения вниз планки 8

( F П1 - F П - F′ ТР )ctgα max = (z - 1)F П nf max .    (9)

Учитывая, что

F′ТР = (z - 1)FП nfmax f1, найдем с учетом соотношения (8)

(tgα) = с + с 1 - f .             (10)

max cnf 1

max

Для того чтобы оценить надежность процесса саморегулирования АФК, установим тенденцию изменения соотношения величин, составляющих левую и правую части исходного равенства (9). Для этого необходимо найти закономерность изменения угла давления по длине опорной поверхности гнезда при движении в направлении его дна.

Решая уравнение равновесия сил, действующих на планку 8 для любого промежуточного положения и учитывая при этом (8), найдем:

с + с1 tgα = i cf max1

+ f 1

2 x i ( с + с 1 ) (z - 1 ) F П fm ax

.

Полученная функция линейная относительно x_i . Для промежуточного положения планки 8 равенство (9) можно записать в виде

(F′ - F - 2x (c + c ) - F - F )ctgα =

П2 П i        1 Рi ТРi        i (11)

= (z - 1)(FП + 2cxi ) nfi .

Так как по условию рассматриваемый АФК обеспечивает постоянство выходного параметра в интервале изменения возмущающего воздействия, можно записать

FР.i = (z - 1)FП fmax ntgαi,

FТР.i = (z - 1)FП n fmax f1.

С учетом этого запишем уравнение (11) в виде

F nl - Л, - 2*z (с + q ) - (- - Wj/тахЛ c + q 2xz(c + q) ‘t/rnax (“ O^nZuax

2(--WCax=0

Коэффициент n , введенный в полученное уравнение, означает, что рассматривается мгновенное фиксированное равновесное положение тел АФК в процессе скольжения фрикционных пар.

Для установления тенденции поведения АФК при уменьшении возмущающего воздействия необходимо определить характер функции, представленной в уравнении первым комплексным членом. Данная функция непрерывна на отрезке 0... x , а ее первая производная также непрерывна и положительна при значениях, определяемых в соответствии с условием

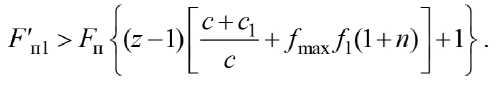
Сопоставление величин F_П1 и F′_П1 по выражениям (8) и (12), показывает что F′_П1 >  F_П1 . Следовательно, найденная сила F_П1 обеспечивает саморегулирование АФК в интервале изменения возмущающего воздействия.

Максимальное вертикальное перемещение планки 8 зависит, очевидно, от необходимой величины изменения суммарного усилия сжатия пружин 11 , измеренного при крайних положениях планки. Это изменение определяется суммарной осевой жесткостью пружин 11 . Поскольку на данном этапе синтеза имеется лишь соотношение между величинами x и c , найденное ранее, величина x определяется также и некоторыми геометрическими параметрами датчика-преобразователя, вначале целесообразно установить величину x .

Для этого воспользуемся расчетной схемой, приведенной на рисунке 3. На схеме показано положение ролика 9 в гнезде, соответствующее нижнему положению планки 8 . Используя геометрические обозначения, можно записать

0,5 D sinαo = 0,5x + 0,5a + l где D – диаметр ролика, a – величина минимального зазора между планками 5 и 8: a = 1...2 мм; l – расстояние между поверхностью планки 5 и параллельной ей плоскостью, проходящей через точку контакта гнезда ролика при его максимальном выходе из гнезда ( l = 2...3 мм).

Найдем:

x = D . =   -a-2l.

Диаметр ролика выбирается по рекомендациям, приведенным в работе [9], в зависимости от величины действующей тангенциальной нагрузки в зоне контакта ролика и гнезда, вычисляемой по соотношению

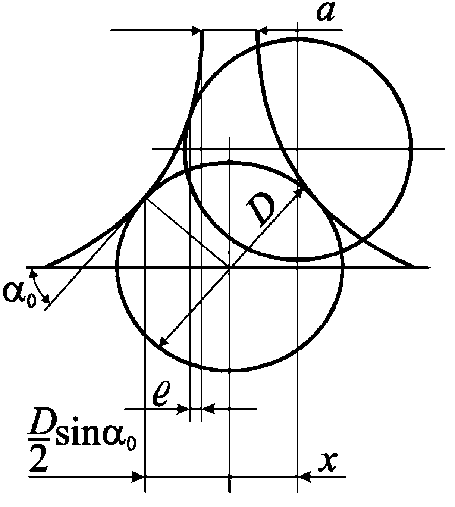
Рисунок 3 – Расчетная схема Figure 3 – Calculation scheme

(z - 1)F_П f_max F_t =     _K

≤ [Ft ].

где K – количество роликов; [F_t ] – допускаемое контактное давление.

По найденному значению x можно определить суммарную осевую жесткость пружин 11 , используя для этого ранее найденное соотношение

с

max min = FП  x f min

На заключительном этапе необходимо найти осевую жесткость пружины 12 .

Определим для этого величину максимального давления ролика 9 , соответствующую крайнему верхнему положению планки 8 . Очевидно, что это соответствует передаче нагрузки при f_max . Ранее было найдено значение параметра ( tgα ) _max , при котором АФК обеспечивает саморегулирование путем перемещения вниз планки 8 под действием силы F_П1 пружины 12 в результате разбалансирования действующих на планку 8 сил из-за уменьшения управляющего воздействия.

Для определения упомянутого угла воспользуемся ранее найденной зависимостью, подставив в которую x_i = 0,5 x , получим с учетом количества пар трения

x(с + с )

(tgα)′ = f +               .

^{max 1} (z - 1)F f

П max

После подстановки значения х в предыдущее равенство получим с + с

(tgα)′ = f +        .

max 1 сf max

Сопоставление (10) и (12) позволяет выявить меньшее значение угла давления, которое должно быть принято при конструировании АФК. Очевидно, что в качестве критерия при определении угла давления должна быть принята возможность саморегулирования АФК при переходе от большей величины возмущающего воздействия к меньшей. Для того чтобы АФК мог проявлять адаптивные свойства в интервале значений fmin ... fmax, необходимо безусловное выполнение условия (tgα)max ≥ (tgα)′max. На основании этого получим с + с1             с + с1

- f1 ≥ f1 + сf , сn max                 max откуда находим

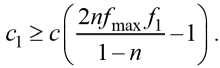
Анализ соотношения (13) показывает, что при реальных значениях n ≤ 0,8, f_max = 0,8...1,0 и f₁ = 0,1...0,15 [9] получается c₁ < 0. Поскольку по физическому смыслу всегда c₁ > 0, полученный результат означает, что поставленное условие, безусловно, выполняется и АФК при принятом соотношении сил F_П , F_П1 и профиле гнезд обеспечивает саморегулирование как при уменьшении, так и при увеличении возмущающего воздействия.

Так как параметр c₁ входит в формулу для вычисления параметра tgα_i и, следовательно, определяет ее, выбор величины c₁ некритичен. Однако для уменьшения веса пружины 12 и силы F_П1 , а также величины перепада последней в результате вертикального перемещения планки 8 целесообразно выбирать пружину с малым значением осевой жесткости c₁ .

Полученные результаты могут быть использованы в практике проектирования и расчета адаптивных фрикционных муфт с положительной обратной связью, обладающих высокой нагрузочной способностью и точностью срабатывания.

ЗАКЛЮЧЕНИЕ

• 1.    Анализ существующей структурно-функциональной схемы АФК показал, что использование принципа непосредственного регулирования с пропорциональным нажатием пар трения невозможно вследствие необходимости дополнительного силового воздействия на упругий элемент. Это обусловливает введение принципа косвенного регулирования, в соответствии с которым сумматор выведен из состава фрикционной группы и является составной частью автоматически регулируемого нажимного узла, а на выход сумматора подаются задающее и управляющее воздействия одного знака.

• 2.    Указанная особенность позволяет производить настройку АФК по максимальной величине возмущающего воздействия и обеспечивает саморегулирование во всем интервале его изменения при более эффективном использовании задающего воздействия.

• 3.    Принцип косвенного регулирования и соответствующая схема АФК предполагают обратную зависимость между управляющим и возмущающим воздействиями, так как управляющее воздействие, формируемое сумматором, реализуется в нажимном узле.

• 4.    Эффективность использования задающего воздействия можно определить по характеру изменения коэффициента рассогласования: убывание его величины при возрастании возмущающего воздействия свидетельствует об эффективном использовании задающего воздействия при заданном уровне выходного параметра АФК и наоборот.

• 5.    Для обеспечения условия саморегулирования в интервале изменения возмущающего воздействия число пар трения АФК должно быть равно отношению верхней и нижней границ этого интервала.