Анализ и синтез инвариантной системы управления электроприводом

При учете компенсирующей связи изображения для регулируемой величины X ( p ) и ошибки системы ε ( p ) соответственно будут равны

X(P)=Ф (P G(P)

,

W ( p )" 1 ₊ ^{W g (} р ) где W ⁽ p ) = W ⁽ pW ⁽ p ) ;  , x       1    W 1 ⁽ p ) . .

Ф ⁽ p )      1 + W ( p )

^( p ) = Ф. ( p )• G( p ),               (2)

где

Ф _£ ⁽ P ) =

1 + Wg (P )• W2 (P ) 1 + W (P )

Из последнего выражения следует условие инвариантности по задающему воздействию

Wg( p )=Xw2 ( p )

.

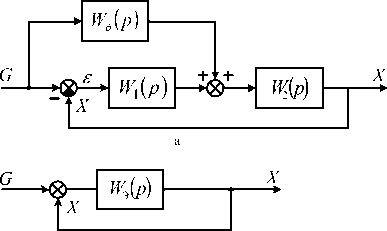
б

в

Рис. 1. Структурная схема системы с инвариантным управлением.

Выполнение условия (3) позволяет устранить вынужденную составляющую ошибки слежения, вызванную изменением управляющего воздействия G ( t ). Разложение в ряд условия (3) позволяет определить формирование компенсирующей цепи

W (P )=k-  W (p )=

p

;

k ₂

p ² ( T 1 P + 1 )

Wg (P ) =

W2 (P )

= т P + TP + •••

Таким образом, в следящих электроприводах для улучшения их работы требуется вводить производные от управляющего воздействия. С повышением порядка производной резко возрастает сложность ее получения (формирования). Это приводит к тому, что полная инвариантность практически недостижима. При формировании реальных компенсирующих цепей вида

где k 1 – добротность системы по скорости, k 2 – добротность системы по ускорению, T 1 , T 2 – постоянные времени.

Допустим, что передаточная функция соответствует выражению (7). Используя (6) найдем W Э ( р ) для случая введения первой производной от входного воздействия τ 1 pG ( p )

W ₃ ( р ) =    k i^{( r} i ^{p +} 1 )

^T 1 p ⁺ p - k_x T _xp

Видно, что условие компенсации скоростной ошибки выразиться формулой τ 1 =1/ k 1 .

При этом выражение (10) примет вид

Wg (P ) = T p + TTT2P- + ••• 1 + т P

W3 (p ) =

к,(т, P +1) = k1 (TP +1)

T 22

₁ p ²           p ²

разомкнутый контур изменяет характеристическое уравнение замкнутой системы. Наличие нелинейности и особенности реализации комбинированного управления приводят к тому, что практически невозможно достичь условий абсолютной инвариантности, в реальных системах, а возможно лишь частичное выполнение этих условий.

Выполним синтез следящего электропривода с комбинированным управлением. На рис. 1б,в приведены преобразованные структуры рассматриваемого электропривода, где

^W3 ⁽ P ) =

Ф(P) _

w (P f¹+ Wn

L    W ⁽ p ) J

Выражения, позволяющие для передаточных функций (7-11) найти условия компенсации, приведены в табл. 1. В результате приведенных расчетов можно синтезировать систему, удовлетворяющую требованиям точности. Однако введение компенсирующих сигналов увеличивает колебательность системы. Рассмотрим структуру рис. 1, звенья которой имеют следующие передаточные функции

W g ⁽ P ) = ^T 1 P;

^{W (} p ) = k;;

w2 (p )= /k 2   x •

^2W p ( Tp + 1 )

Ф

1 - Ф ( P )     1 - W g ( P ) W 2 ( P )

1+ Wg (P ) W (P )

W 1 ( p ) 1 + W ( p )

;

Из таблицы 1 находится уровень компенсирующего сигнала τ 1 =1/ k 2. В [3] получены формулы, позволяющие определить показатель колебательности M в случае симметричной ЛАХ

Точность следящей системы определяется в основном свойствами в низкочастотной области. По этому влияние компенсирующих сигналов W д ( р ) можно учитывать только в этой области. Инвариантные сигналы не влияют на характер свободного движения системы, поэтому среднечастотная часть формируется без их учета. В низкочастотной области передаточная функция следящих систем может иметь следующий вид

n

I Tj5 - j=g+1      too

1M (M +1)

M + 1

и в случае несимметричной ЛАХ

n

kIT 5

i = 1

m ² + m4m ² - 1

Используя выражение (13) для рассматриваемой системы получаем выражение

^{W ( P} ) = PTp+D:

;

^{W ( p} ) = p ( T 1 p + 1 ) ( T ₂ p + 1 ).

;

к 1 ^К 2 Т ⁵

м ² + м4м ² - 1

Таблица 1. Компенсация скоростной ошибки

Исходная передаточная функция для низкочастотной области	Компенсирующая цепь	Уравнение низкочастотной асимптоты эквивалентной ЛАХ	Условия компенсации
к 1	Т 1 Р	k 1 T1 ® 2	1 Т 1 = k 1
Р ( т 1 Р + О	ЧЧ Р 2 Т Р + 1 2  . т 3 Р + 1	k т 3 T 1 ® 3	т 1 = 1 / k 1 Т 2 = T 1
k i	Т 1 * р	k ( T 1 + T 2 ) ® 2	т 1 = 1 / k 1
Р ( T 1 Р + 1 )( T 2 Р + О	ЧЧ Р 2 Т Р + 1 2  . т 3 Р + 1	____________k 1____________ [ T 1 T 2 + Т 3 ( T 1 + T ) ] ® 3	Т 1 = 1/1 т 2 = T 1 + T 2 + т 3
k 2 Р 2	2  2 т 2 Р	k 2 Т3№*	т 2 = 1/ k 2
k- 2 Р 2 ( TР + 1 )	т 3 Р + 1	k 2 ( T 1 + т 3 ) ^3

Использование цифро-аналоговой структуры (рис. 2) электропривода позволяет получить следующие преимущества перед аналоговыми или цифровыми системами: - относительная простота устройства;

• -    высокая гибкость структуры и возможность реализации инвариантных цепей и высокого порядка;

• -    высокая точность и надёжность.

Наиболее целесообразной является структура подчинённого регулирования, когда регулируемый привод (система стабилизации) выполнен в виде аналоговой системы, а регулятор положения (РП) и инвариантные цепи (ИЦ) реализуются программно в управляющем микропроцессоре. Считаем, что аналоговая часть (регулируемый привод) настроена на модульный оптимум и имеет передаточную функцию вида

Wl ( Р ) = --- 7 7  -------

• ²       2T ² p ² + 2 Tp + 1

, где К - коэффициент передачи регулируемого электропривода; Т - постоянная времени электропривода.

Структура следящего привода приведена на рис. 1а.

При учете компенсирующей связи изображения для регулируемой величины X(р ) и ошибки системы е(р ) соответственно будут равны

X ( Р ) = Ф ( Р G ⁽ Р )

,

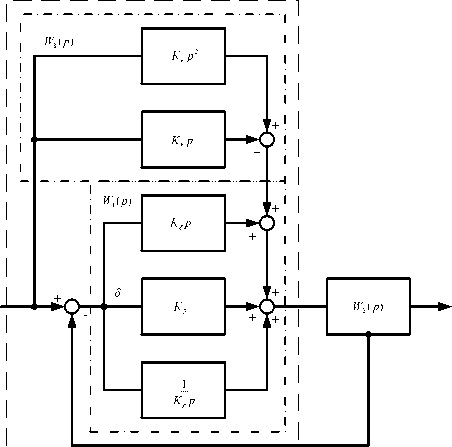
Рис. 2. Функциональная схема цифроаналогового электропривода

В результате применения такой коррекции повышается астатизм системы, а в передаточной функции замкнутой системы появляются форсирующие составляющие в числителе. На рис. 3-3 приведены осциллограммы переходных процессов в электроприводе ( V_ВЫХ ) на задающий сигнал по скорости ( V ЗАД ) с введением различных инвариантных сигналов:

• -    по первой производной К у ,

• -    по второй производной К У ;

• -    по третьей производной K S .

  
  
  
  

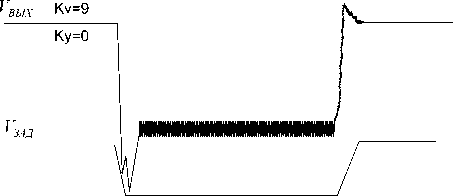
  Рис. 3. Переходный процесс по скорости системы с введением первой производной

  
  
  
  
  
  
  
  
  
  
  

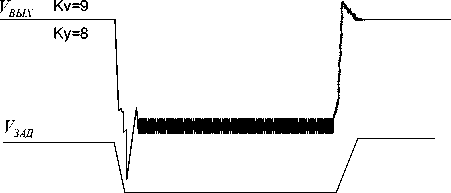
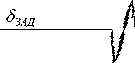
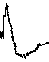
Рис. 4. Переходный процесс по скорости системы с введением первой и второй производных

Моделирование исследуемой системы показало эффективность применения упреждающей коррекции для снижения динамических ошибок без повышения колебательности [4].

Выводы:

• 1.    Увеличение количества инвариантных сигналов приводит к снижению амплитуды динамической ошибки;

• 2.    Введение сигнала по третьей производной и выше приводит к нарастанию пульсаций скорости;

• 3.    Инвариантные цепи повышают колебательность системы, поэтому необходимо контролировать (ограничивать) динамические параметры задающего сигнала;

• 4.    Для снижения динамических ошибок системы можно использовать упреждающую коррекцию.

  

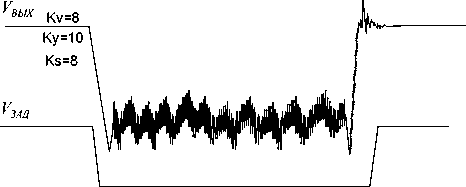
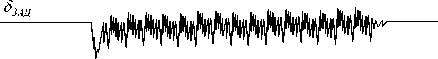
Рис. 5. Переходный процесс по скорости системы с введением первой, второй и третьей производных