Анализ и синтез широтно-импульсных систем

Системы автоматического управления с широтноимпульсной модуляцией (ШИМ) относят к классу нелинейных импульсных. Подобные системы известны достаточно давно и в настоящее время широко применяются, однако разработанных методик анализа и синтеза, особенно для инженерных приложений, практически нет.

Предлагаемые методики анализа и синтеза систем с ШИМ позволяют решить большинство из тех задач, которые при этом возникают: исследовать устойчивость системы и в малом, и в большом; изучить динамические характеристики системы с учетом инерционности ШИМ-ключа; дать оценку увеличения или уменьшения запасов устойчивости при работе системы в нелинейных режимах, объяснить причину возникновения в системе многочастотных колебаний; синтезировать корректирующие устройства, обеспечивающие необходимые запасы устойчивости, построить управление, обеспечивающее системе с ШИМ оптимальность по быстродействию.

Разработанные методики анализа и синтеза основываются на представлении системы с ШИМ как существенно нелинейной системы автоматического управления [1], включающей в себя релейно-гистерезисный элемент с зоной нечувствительности, отражающий реальные характеристики любого ключевого элемента, непрерывную нелинейную часть, содержащую звено запаздывания, отражающее инерционные свойства ключа, на которую воздействует постоянная составляющая и периодическое (пилообразное, треугольное или синусоидальное) внешнее воздействие (рис. 1). Передаточная функция W _oc( p ) вводится при коррекции динамических характеристик системы.

Такой подход дает возможность применять методы исследования существенно нелинейных систем и на их основе разработать методики анализа и синтеза систем с ШИМ, позволяющий эффективно решать задачи обеспечения устойчивости для линейных и нелинейных режимов, более корректно сформулировать условия перехода от нелинейной к квазинепрерывной модели, решать задачи построения многомодульных широтно-импульсных систем (ШИС).

Рис. 1. Структурная схема широтно-импульсной системы

Система автоматического регулирования (см. рис. 1), относится к классу нелинейных систем, так как содержит существенно нелинейный элемент с релейно-гистерезисной характеристикой. К системе приложены внешние воздействия: постоянное (опорный сигнал) и в виде периодических колебаний, в общем случае пилообразных, треугольных или синусоидальных, которые заставляют рассматриваемую систему работать в режиме вынужденных колебаний.

В подавляющем большинстве практических случаев передаточная функция линейной части W_nH(p ) в ШИС обладает свойством фильтра [1]:

I WJjn ® ) 1 << 1 WJ' ® ) l , n = 2,3,....

Это следует из самого назначения непрерывной линейной части снижать уровень пульсаций на выходе системы. Следовательно, для анализа устойчивости и синтеза подобной системы может быть применен метод гармонического баланса (гармонической линеаризации), являющийся до настоящего времени самым мощным средством анализа и синтеза существенно нелинейных систем автоматического регулирования и управления.

С точки зрения метода гармонического баланса задача исследования устойчивости рассматриваемой схемы сводится к определению условий возникновения автоколебаний в системе при наличии вынужденных колебаний и постоянной составляющей.

Уравнение динамики системы имеет вид [1]

X+ W> ) e-* p W o>) F [ X ] = W >) U о _п - f „( t ), (1) где ^f J t ) = ^{B Sin( Ю} 2 ■ t )-

Решение уравнения находится в виде

^X = X B ⁺ X м ,                (2)

где X м = X 0 + X A ; X м - медленно меняющаяся составляющая; X , - постоянная составляющая; X A = A ■ sin( ro , ■ t ) -переменная составляющая, характеризующая автоколебания; X B = A 2 ■ sin( m ₂ ■ t + ф ) - переменная составляющая, характеризующая вынужденные колебания в системе; ю , - частота автоколебаний, ю ₂ = 2 п / T - вынужденная частота; T - период переключения.

При использовании принятых обозначений уравнение (1) разбивается на два уравнения соответственно для медленно меняющихся и колебательных составляющих:

Q ( p ) ■ X n + R ( p ) e^p ■ W ( p ) ■ F ⁰ = = W o.c ( P ) ■ U оп ■ Q ( P ) ,

^[ Q ⁽ p ) + R ⁽ p ) e ^: p W o.c ⁽ p ) ■ ⁽ q + qp / w 2 ) +

+ Q ( p ) B (cos ф- sin ф^ p/w ₂)/ A 2 ] ■ X B = 0,    (3)

где принято W _JIH( p ) = R(p )/ Q(p ).

Нелинейность и коэффициенты гармонической линеаризации определятся из выражений

F [ X ] = F ⁰( A , X м ) + [ q ( A , X м ) + q ' ( A , ) ■ p / w 2 ] ■ X b ,

X

q ( A , X ) =    ¹ x

2м

A 2 "П

( I----~--------7

L ( b - X м )²

А ¹ I 2

( b + X м )²

Л 2

q ‘ ( A ) = - '^ b , A 2 ■п

F ⁰( A , X„ ) = — + U- ■ arcsin 2м

2 2 ■п I

- arcsin

Амплитуда A ₂ определяется из равенства

A 2 = B,_____________________ I Q ( ' - ) 2 _____________________

I Q(j _Ю2 ) + R(j ® 2 ) ■ e' ■ W oe (J -) ■ ( q + jq ')² 1 .

Решая (3), можно определить функцию смещения

F ⁰( A ₂, X _м) = Ф( Х _м)                (5)

для заданной нелинейности F [ X ], которая в дальнейшем используется при определении автоколебательного режима и решения уравнения для постоянных составляющих. Для этого линеаризуем функцию смещения Ф( Х _м) в пределах рабочего режима системы

Ф ( X м ) = Ф 0 + K A ■ X A ,            (6)

dФ гдек‘ = dA м

-

м = X 0

С учетом (4), (5) и (6) система уравнений для определения возможности возникновения автоколебательного

режима имеет вид

Q (0) X ₀+ R (0) W _o.c(0)Ф⁰ = W _oc(0) U _оп Q (0),

Q ( p ) X_A + R ( p ) e ^{-t p}W _o.c(p) K_AX_A = 0.          (7)

После подстановки в (7) p = jw ₁ определяются X ₀, A ₁ и w ₁, т. е. условия возникновения или отсутствия автоколебаний в системе, на основании чего делается заключение об устойчивости системы. Изменяя W _л.ч( p ) или вводя корректирующие устройства в цепь обратной связи, т. е. также изменяя W _o.c( p ) и используя вышеизложенную методику, можно синтезировать рассматриваемую ШИС исходя из необходимых запасов устойчивости.

Наличие вынужденных колебаний в системе приводит к эффекту вибрационной линеаризации нелинейности [3]. В этом случае релейно-гистерезисный элемент приобретает квазинепрерывную нелинейную характеристику, зависящую от параметров непрерывной линейной части и нелинейности. Однако такая нелинейная характеристика с большим основанием может быть линеаризована в рабочей точке, чем релейно-гистерезисная. Если в выражении для коэффициента F ⁰(4) принять Х _м = Х ₀, то согласно (6) коэффициент передачи линеаризованной нелинейности определится выражением

K

А

U l f        1

Ц v А 2 ² - ( b + X 0)²

4А 2 2 ^{- (} b ^{- X} 0 ⁾²

)

, (8)

где А ₂ – амплитуда вынужденных колебаний; Х ₀ – постоянная составляющая на входе нелинейности. Для предва-

рительных расчетов значение коэффициента K_А приближенно определяется исходя из требований к синтезируемой системе. Если принять W _o.c( p ) = 1, то при заданных

статической точности Х ₀ и пульсациях А U , на стадии предварительного проектирования А ₂ определяется приближенно: А ₂ ® В - D U ₂.

Таким образом, ШИС можно представить в виде квазилинейной системы с передаточной функцией разомкнутого контура W_p ( p ), определяемой выражением

W_p ( p ) = K_A W _л.ч( p ) W _o.c( p ) e ^{–t p} . (9)

Как показывают исследования, выражение (9) с высокой степенью точности может быть использовано для анализа устойчивости и синтеза ШИС с целью обеспечения заданных запасов устойчивости.

Рассмотренная структурная схема является классической при решении задачи построения системы, оптимальной по быстродействию [4]. В соответствии с теорией оптимального управления, произведение e^{–t p} W _л.ч( р ) является объектом управления (ОУ), F [ X ] выдает управляющее воздействие, ограниченное сверху U ₁ и снизу 0. Сама функция F [ X ] имеет релейную характеристику, что, в соответствии с принципом максимума Л. С. Понтрягина, необходимо при построении оптимальной по быстродействию системы и наличии ограничений на величину управляющего воздействия.

На основании вышеизложенного задача синтеза ШИС по критерию оптимального быстродействия сводится к определению условий переключения релейного регулирующего элемента F [ X ], т. е. нахождению уравнения линии переключения [3; 4]. Применительно к схеме (см. рис. 1) задача синтеза предполагает нахождение такой передаточной функции W _o.c( p ), которая обеспечит оптимальное быстродействие системе.

Решение вышеприведенной задачи осуще ствляется с применением метода фазовых траекторий и сводится к определению уравнения оптимальной фазовой траектории для объекта управления.

Для простейших случаев уравнение оптимальной фазовой траектории можно получить аналитически. В большинстве практических случаев этого сделать не удается. Методика построения оптимального по быстродействию ШИС в этом случае выглядит следующим образом. По известной передаточной функции объекта управления рассчитываются фазовые траектории и определяется оптимальная. Оптимальная траектория аппроксимируется. Полученное уравнение аппроксимации принимается за уравнение линии переключения теперь уже квазиоптимальной по быстродействию ШИС.

Следует отметить, что сложность решения задачи построения оптимальной по быстродействию системы в значительной степени зависит от вида передаточной функции объекта управления. Изложенная выше методика более справедлива для систем второго порядка без учета запаздывания. Для этого случая важную роль будет играть вид корней характеристического уравнения объекта управления. В случае простых корней, согласно теореме об n -интервалах, оптимальная система отрабатывает возмущение за два интервала постоянства. Если корни комплексные, то количество интервалов постоянства зависит от уровня возмущающего воздействия. Последнее утверждение справедливо и для систем более высокого поряд-

ка, но для таких систем сложно, а часто и невозможно использовать метод фазовых траекторий.

Предложенная выше методика построения оптимальной по быстродействию системы справедлива для больших отклонений и не учитывает наличия внешнего периодического воздействия. Однако и в этом случае, как показано в [3], можно использовать метод фазовых траекторий для анализа поведения ШИС в режиме вынужденных колебаний.

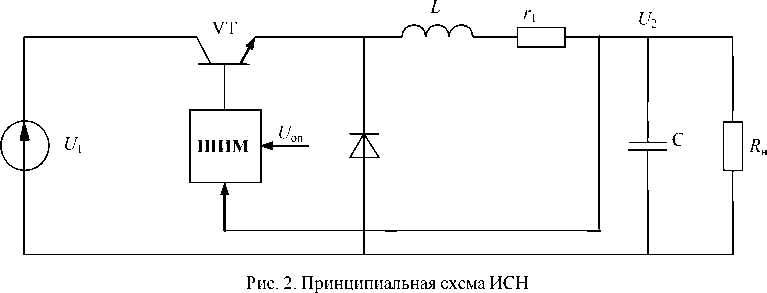
Рассмотрим применение вышеизложенных методик на примере анализа и синтеза импульсного стабилизатора напряжения (ИСН) понижающего типа (рис. 2).

Нелинейная модель ИСН может быть представлена в виде схемы (см. рис. 1). Линейной частью ИСН является однозвенный фильтр с передаточной функцией вход фильтра – выход фильтра с учетом параметров нагрузки:

= ^KC

Wл.ч(р) a2⋅p2 +a1⋅p+1, где KC=Rн(Rн+r1) – коэффициент передачи; Rн – сопротивление нагрузки, r1 – активное сопротивление обмотки дросселя фильтра; L – индуктивность дросселя фильтра; C – емко сть конденсатора фильтра; a2 =KC⋅L⋅C; a1=(L+Rн⋅r1⋅C)(Rн+r1). Нелинейность F[X] и звено чистого запаздывания e–tp имитируют работу импульсного ключа VT, управляемого ШИМ. В общем случае ШИМ состоит из компаратора, на один из входов которого подается пилообразное напряжение (Uпил), а на второй – управляющее (сигнал ошибки) напряжение (Uоп – U2). При анализе ИСН считалось, что на вход компаратора вместо Uпил действует синусоидальное напряжение с такой же амплитудой. Величина амплитуды принималась исходя из допустимой статической ошибки менее 1 %. На основании вышеизложенного метода при разработке нелинейной модели ИСН напряжения Uпил и Uоп моделируются источником вынужденных колебаний fвын(t) и постоянной составляющей соответственно.

Расчеты проводились при следующих исходных данных: частота преобразования 25 кГц; U ₁ = 40 В; U _оп = 27 В; L = 10 мкГн; C = 5 мФ; r _l = 0,010 м; t = 1 мкс; R о _н = 10 м; В = 0,2 В; W _o.c( p ) = K – передаточная функция звена обратной связи; K = 1; b – зона нечувствительности компаратора, b = 0,001.

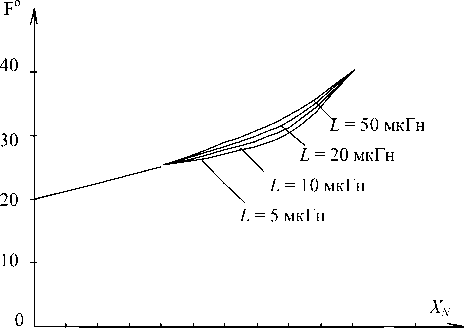
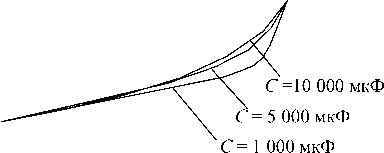
Согласно [2], процессы в ИСН описываются уравнением динамики (1). Решение этого уравнения ищется в виде (2) из системы уравнений (3) для медленно меняющихся и колебательных составляющих. Решая (3), определяем функцию смещения (5) и линеаризуем ее в преде- лах рабочего режима ИСН (6). Из рассчитанных функций смещения (рис. 3) при различных значениях параметров фильтра (индуктивностях – рис. 3, а и емкостях – рис. 3, б) следует, что значение KА в рабочей точке равно14…15.

Уравнение (1) теперь примет вид (7) и неизвестные A ₁, ω ₁ и X ₀ определяются из (7) подстановкой p = j ω ₁:

1-a2⋅ω12 +KА⋅KC⋅K⋅cos(ω1⋅τ)=0, a1⋅ω1-KА⋅KC⋅K⋅sin(ω1⋅τ)=0,

X 0 + K C ⋅ K ⋅ Ф⁰ = K ⋅ U оп .           (10)

При решении (10) f1 должно быть меньше 25 кГц. Тогда величина 2πf1⋅t = ω1⋅t мала и sin(ω1⋅ t) ≈ ω1⋅τ, а cos(ω1⋅τ) ≈ 1. Отсюда искомое решение для автоколебаний системы, т.е. условие их существования определится из выражения r⋅C+LY-K⋅τ⋅K=0.          (11)

1н                A

При подстановке значений параметров в (11) следует, что в системе отсутствуют автоколебания. Однако если совместное запаздывание ключа и компаратора будет равно 4 мкс, то в системе возникнут автоколебания с частотой 2,7 кГц.

Для анализа динамических характеристик ИСН как квазилинейной системы передаточную функцию разомкнутого контура представим согласно (9), где K_A = 15 (рис. 4). Построим логарифмическую амплитудную (рис. 4, а ) и фазочастотную (рис. 4, б ) характеристики ИСН (сплошная линия). Там же пунктирной линией изображены аналогичные характеристики скорректированной системы, когда

W о.с ( p ) =

1 + T 1 ⋅ p _, 1 + T 2 ⋅ p

при Т ₁= 1,25 мс, Т ₂= 0,125 мс.

Параметры корректирующего устройства выбирались исходя из заданного запаса по фазе a = 60°, который обеспечивает корректирующее устройство на частоте среза системы.

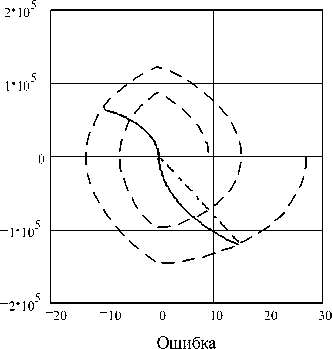
В соответствии с изложенной выше методикой синтеза оптимальной по быстродействию широтно-импульсной системы, используя передаточную функцию (10), строим фазовые характеристики и определяем оптимальную траекторию (расчеты в пакете Mathcad) (рис. 5). Штриховой линией показаны фазовые характеристики исходной нескорректированной системы, сплошной линией – оптимальная траектория, штрих-пунктирной – ква-зиоптимальная (рис. 5, а ). Поскольку аналитически определить выражение, описывающее оптимальную линию переключения, практически невозможно, была проведе-

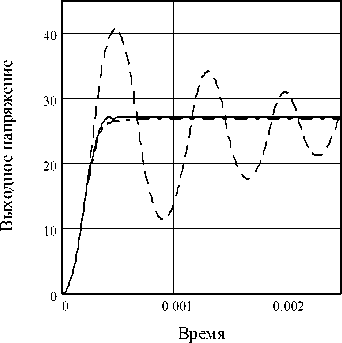
на ее аппроксимация, которая позволила получить выражение для линии переключения X + 1,01 - 10 " 9 ■ X ² ■ sign( X ) = 0. Квазиоптимальная линия переключения (см. рис. 5, а ), имеет вид X + 1,3 ■ 10 - 4 ■ X = 0. Переходные процессы в ИСН при включении напряжения питания для трех случаев: нескорректированной системы, с квадратичным (сплошная линия) и линейным (штрихпунктирная линия) законами управления электронным ключом ИСН – приведены на рис. 5, б .

Справедливости ради следует отметить, что результаты расчетов (см. рис. 5) получены без учета нелинейной характеристики диода. В реальной схеме без корректирующего устройства наблюдается режим прерывистых токов и переходной процесс не является колебательным. Однако и в этом случае (рис. 6) (расчет с помощью пакета MicroCAP) введение коррекции с рассчитанными параметрами обеспечивает системе оптимальность по быстродействию, что подтверждает правильность предложенной методики синтеза.

Fо

б

Рис. 3. Функции смещения: а – при различных индуктивностях; б – при различных емкостях фильтра

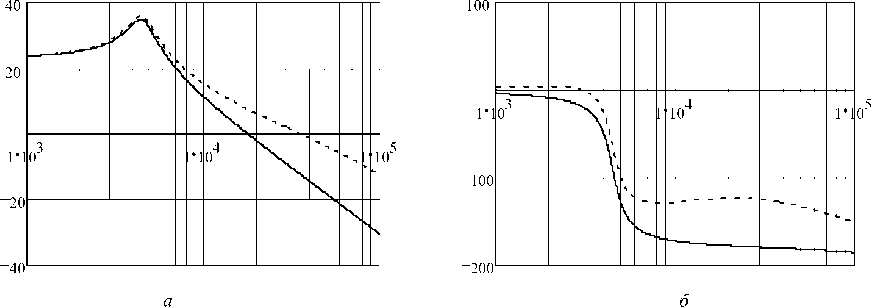
Рис. 4. Характеристики ИСН: а – логарифмические; б – фазочастотные

а                                                        б

Рис. 5. Характеристики нескорректированной и оптимальной системы: а – фазовые характеристики; б – переходные процессы

Предложенные методики дают возможность с единых позиций, используя хорошо апробированные методы, с высокой точностью решать задачи анализа и синтеза ШИС: оценивать устойчивость системы и синтезировать ее, исходя из заданных запасов устойчивости, строить оптимальную по быстродействию систему. Данные методики хотя и позволяют уже сейчас решать большое количество задач, связанных с ШИС, однако требуют развития для решения более сложных проблем, например, проведения анализа и синтеза при наличии дополнительных нелинейностей в ШИС, построения оптимальной по быстродействию системы высокого порядка.