Анализ и синтез управления авиационной транспортной системой гражданской авиации

есть с условиями полета (L-E), человек - с техническим устройством (машиной), то есть с воздушным судном или оборудованием ВС (L-H). Важной составляющей модели является цепочка, затрагивающая схему SHELL - взаимодействие между людьми.

В отечественной литературе [5-7] АТС обычно представляют в виде структуры, показанной на рис. 2.

При системном подходе АТС представляет собой сложную систему, части которой можно рассматривать как системы, закономерно объединенные в единое целое в соответствии с определенными принципами и связанные между собой заданными отношениями. Она включает в себя следующие системы: экипаж - воздушное судно, службу управления воздушным движением, службы обеспечения полетов, каждая из которых может рассматриваться как самостоятельная система. АТС относится к классу интеллектуальных систем, так как составляющие АТС представляют собой человеко-машинные системы.

Произведем решение задачи анализа и синтеза управления АТС в целях исследования индикаторов качества управления интеллектуальной системы АТС, и для этого воспользуемся интервальными и неясными методами [9]. Применение этих методов вызвано несоответствием данных и параметров АТС, которой присущи только статистические данные воздействия АТС на безопасность полетов. Разработаем новый подход к управлению АТС, не нарушая принятой ICAO модели SHEL и дополняя концепцию ICAO [3, 4] по организации управления безопасностью полетов, направленной на снижение факторов риска, и рассмотрении влияния организационных процессов при управлении воздушным судном. В данной статье решение задачи параметрического синтеза управле-

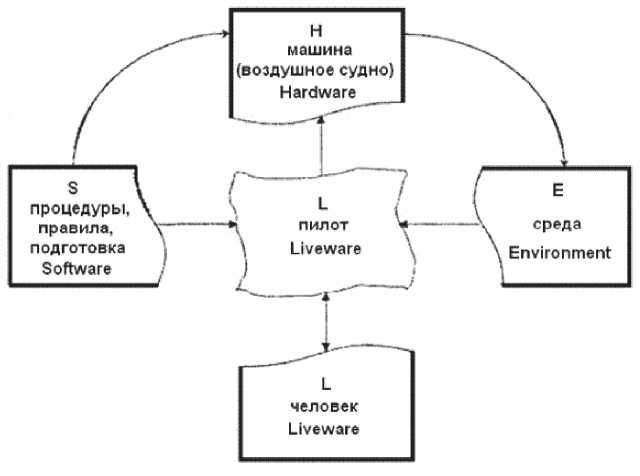
Рис. 1. Компоненты и интерфейсы модели SHELL

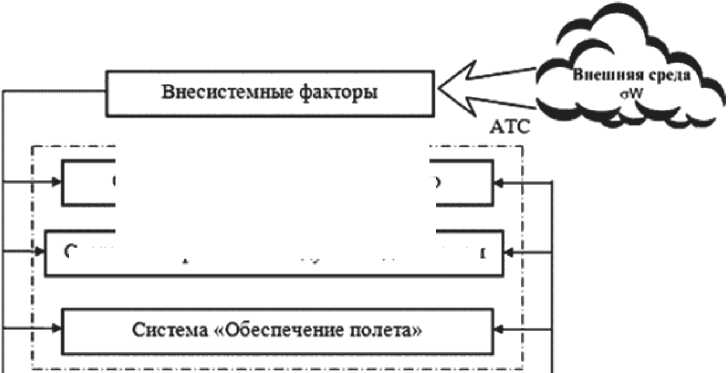
* Система «Управление летной деятельностью»

Рис. 2. Структура ATС

Система экипаж - воздушное судно

Система «Управление воздушным движением

ния интеллектуальной системы АТС с неточными данными выполним с помощью метода интервального анализа [10].

Утверждение задачи.

Примем, что математическая модель АТС представляет собой мультивариантную модель управления неуверенным объектом, показанную на рис. 3.

В соответствии с рис. 2 АТС имеет m входов и m выходов и, таким образом, имеет m каналов. При применении метода синтеза в классе многомерных систем должно выполняться условие: каждый канал должен быть развязан от остальных, независим и автономен. В системе АТС управляемыми переменными являются управление экипажем воздушным судном, управление движением воздушных судов, управление обеспечением полета, управление летной деятельностью и др.

В данном случае Lf(t) — [iij(t) u2(t) Из(0"" ] и jf(t) — [^(t) X2(t) хз(0 ’1'

При исследовании системы АТС, а также при синтезе АТС необходимо учитывать перекрестные связи - влияние на действия экипажа системы управление воздушным движением, системы обеспечение полета, системы управление летной деятельностью и др. (сигнал u ₁( t ) воздействует на выход x ₂( t ), u ₂( t ) воздействует на выход x ₁( t ), и т.д.)

Управление АТС выглядит следующим образом

X(t) = ЛХ(0 + BU(t) , (1) где X ( t ) – n мерный вектор состояний;t/(t)- m мерный вектор управляющих воздействий; A и B – интервальные матрицы управления АТС.

Задачей синтеза будем считать определение матрицы интервалов K в уравнении обратной связи

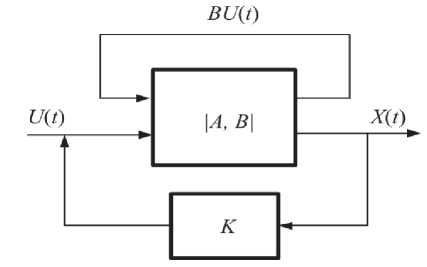
Рис. 3. Модель АТС: векторный входной сигнал, вектор состояния АТС;

A и B – интервальные матрицы управления АТС;

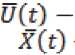
K – матрицы интервалов - отрицательная обратная связь устойчивого управления; BU(t) - вектор-функция управления АТС

= K ,           (2)

обеспечения желательных динамических свойств закрытой системы АТС, которая представлена в следующем виде

( t ) =       - BK =( A - BK )     = D , (3)

где D – интервальная матрица управления закрытой системы АТС.

Интервальную полиномиальную характеристику закрытой системы АТС представим в виде

[d( X )]=det(AI-D)= X n+[d Jn-1 +- + [dn], (4) где [di], i =     – интервальный номер полино миальной характеристики.

Алгоритм решения задачи синтеза АТС бу- дет состоять из двух следующих шагов.

Шаг 1 :

Решение параметрической задачи синтеза управления мультивариантного стационарного объекта АТС, принадлежит семейству (1).

Прежде, чем непосредственно перейти к решению задачи синтеза семейства ценностей математической модели (1) рассмотрим математическую модель с установившимися параметрами элементов матриц A и B , т.е. математическую модель следующего вида

( t ) = ( A                + ( t ),          (5)

где A , B и K – постоянные матрицы.

Для замыкания обратной связи необходимо знать вектор состояний . Последний оценивается с помощью наблюдающих устройств кабины экипажа.

Для модели (5) уравнение обратной связи будет представлено следующим образом

,              (6)

где K – матрица отрегулированных параметров, на определение которых ответит решение задачи синтеза для постоянного управления АТС, выполним по методике, предложенной в [11].

Шаг 2 :

Решение параметрической задачи синтеза для мультивариантного управления АТС, базируется на методе обычных параметров и матрицы, найденного выше K как начальное приближение решения задачи синтеза управления путем увеличения колонки матрицы K общих параметров Р :

^^и-

К =    :       ::

РКт2 - Ктп

В - О

К = К :   ::

о - Vi

Вместо выражения (2) запишем

(t).(7)

Характеристику управления полиномиальной модели АТС представленной в виде (7) за- пишем в следующем виде

Параметр Р должен быть равен желательной характеристики полиноминальной модели АТС представленной в виде (4).

Приравнивая идентичные коэффициенты степени X в выражениях (8) и (4), получаем систему линейных алгебраических интервальных уравнений для определения параметра Р .

Рассмотрим уравнения полученной модели, которая имеет вид

[ P ( в _i)]=                                             , (9)

где ,     ,      - интервальные размеры, за висящие от элементов матрицы A, B и K.

Формальное раскрытие устанавливает систем- ную композицию в следующем виде выражения

[ ( в i )] =                      .

Согласно субдистрибутивному закону интервальной математики для набора Р имеем:

[P(в)]                     .(11)

Параметр Р i ₌ ^i найдем из выражения

[ ( i]=                              .(12)

Найденное значение Р _iзаменим в [ P ( в i )]

[ ( i] М [ ( )]          .(13)

Таким образом, получен в виде найденного коэффициент желательного характеристическо- го уравнения управления закрытой системы АТС.

Уравнение (13) согласно алгоритму синтеза преобразовываем к виду

_i [ ]                                  .       (14)

Возможность такого преобразования опреде- лена с помощью действия размещения суммированием [11].

Решение полученной системы (15) дается со следующей теоремой: параметр _i, i = имеет решение невырожденной системы линейной алгоритмической вставки только в том случае, когда это представляет решение системы уравнений im                                .        (15)

Также удовлетворяет ограничениям i S( )                       ,         (16)

где m ( q _i), m ( H _i) – центры и S ( ) 5№) длины интервальных номеров [ ]

В уравнении (16) последовательность параметров _i i = найдена при условии минимального значения отрегулированного параметра

Положим, что АТС является асимптотически устойчивой. Изложим некоторые рассуждения касающиеся влияния каналов в терминах передаточных функций. Связь между входом и выходом АТС задана формулой

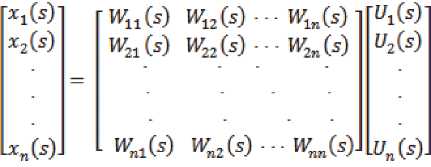
Рассмотрим 1-й выход АТС:

X ₁( s ) = W ₁₁( s ) U ₁( s )+ … + W _1n( s ) U _n( s ).

В АТС 1-й выход определяется 1-м входом (основным входом). Кроме того на 1-й выход оказывают воздействие все остальные входы.

Независимость выходных переменных от других входов, кроме соответствующих входных воздействий, т.е. u 1 ( t ) ^ x 1 ( t ), i = 1. '1 означает, что передаточные функции перекрестных каналов должны обращаться в нуль.

Таким образом, необходимым и достаточным условием автономности каналов является диагональность передаточной матрицы АТС, т.е. должна иметь место зависимость

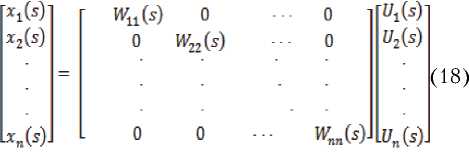
В реальной системе АТС перекрестные связи отличны от нуля и, следовательно, качество работы каждого канала зависит как от свойств собственно канала, так и от характера перекрестных связей.

Задачей синтеза является определение матрицы интервалов K в уравнении обратной связи (2). В программной среде LabView была создана модель определения матрицы К. Зная значение трехмерного вектора состояний X(t) и трехмерного вектора управляющих воздействий U(t), находим трехмерный вектор K.

u(t)

к = —=-—

.

В программной среде задаются численные значения матриц U(t) и X(t), на выходе модели получаем численные значения матрицы интервалов K. Работа модели представлена на рис. 4, а результаты вычисления – на рис. 5.

Таким образом, разработан алгоритмический аппарат, ориентированный на конкретную задачу управления авиационной транспортной системой и обеспечения приемлемого уровня безопасности полетов гражданской авиации.

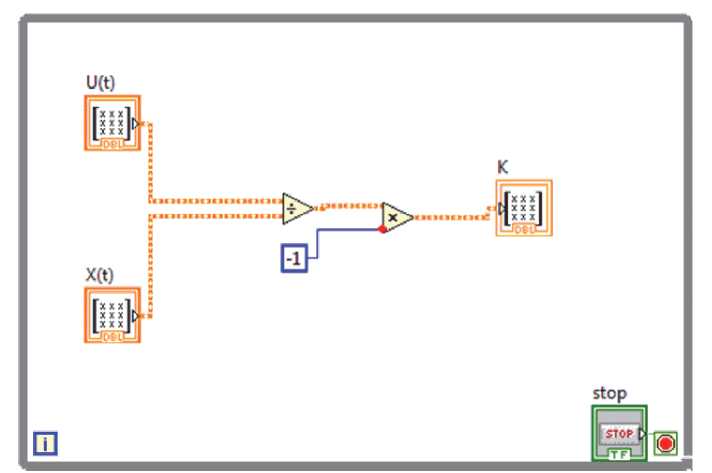
Рис. 4. Блок-диаграмма модели

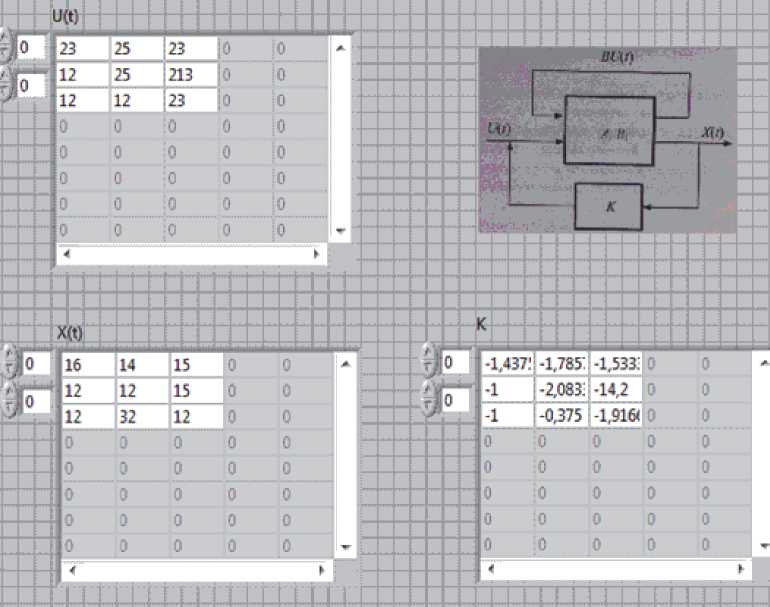
Рис. 5. Лицевая панель модели в программной среде LabView