Анализ и сравнение методов обучения нейронных сетей

Введение. Искусственные нейронные сети находят применение при решении сложных задач, когда обычные алгоритмические решения оказываются неэффективными или невозможными. При построении нейронных сетей делается ряд допущений и значительных упрощений, однако, они демонстрируют такие свойства, как обучение на основе опыта, обобщение, извлечение существенных данных из избыточной информации. После анализа входных сигналов нейронные сети самонастраиваются и обучаются, чтобы обеспечить правильную реакцию. Обученная сеть может быть устойчивой к некоторым отклонениям входных данных.

Рассмотрим многослойную полносвязанную нейронную сеть прямого распространения (рис. 1), которая широко используется для поиска закономерностей и классификации образов. Полносвязаиной нейронной сетью называется многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми нейронами предыдущего слоя (нейроны первого слоя соединены со входами нейронной сети). Прямое распространение сигнала означает, что такая нейронная сеть не содержит петель. Математическая модель нейрона описывается выражением (1)

^■^ =■ /£ ^^^ С1)

j=i где I - выход нейрона, верхний индекс (г) показывает номер слоя, нижний индекс (/с) показывает номер нейрона в слое; N - число нейронов в слое; ш - вес синаптической связи; / - функция активации нейрона.

Выход А’-го нейрона слоя г-4-1 рассчитывается как взвешенная сумма всех его входов со слоя г, к которой применена функция активации, нормализующая выходной сигнал. Входы нейронов слоя г + 1 являются выходами нейронов слоя г.

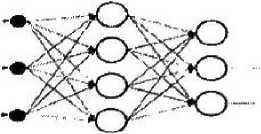
Рис. 1. Пример многослойной полносвязанной нейронной сети прямого распространения сигнала

Целью данной статьи является сравнение градиентных методов обучения нейронных сетей. Ставится вопрос об улучшении задачи поиска глобального минимума функции энергии с применением теории вейвлет-пре-образований.

Рассмотрим понятие и принципы процесса обучения многослойной нейронной сети (многослойного персептрона). Уделим внимание основному методу обучения многослойного персептрона - алгоритму обратного распространения ошибки - и его модификациям. Сравним эти методы обучения, определим достоинства и недостатки, а также предложим иной подход к решению задачи поиска глобального минимума функции энергии.

Обучение [2]. Для нейронных сетей под обучением понимается процесс настройки архитектуры сети (структуры связей между нейронами) и весов синаптических связей (влияющих на сигналы коэффициентов) для эффективного решения поставленной задачи. Обучение нейронной сети осуществляется па определенной выборке по некоторому алгоритму.

Выделяют три парадигмы обучения: с учителем, без учителя (или самообучение) и смешанная. Среди множества алгоритмов обучения с учителем (когда известны праг вильные ответы к каждому входному примеру, а веса подстраиваются, чтобы минимизировать ошибку) наиболее успешным является алгоритм обратного распространения ошибки. Его основная идея заключается в том, что изменение весов синапсов происходит с учетом локального градиента функции ошибки. Разница между реальными и правильными ответами нейронной сети, определяемыми на выходном слое, распространяется в обратном направлении (рис. 2) - навстречу потоку сигналов. Б итоге каждый нейрон способен определить вклад каждого своего веса в суммарную ошибку сети. Простейшее правило обучения соответствует методу наискорейшего спуска, то есть изменения синаптических весов пропорционально их вкладу в общую ошибку.

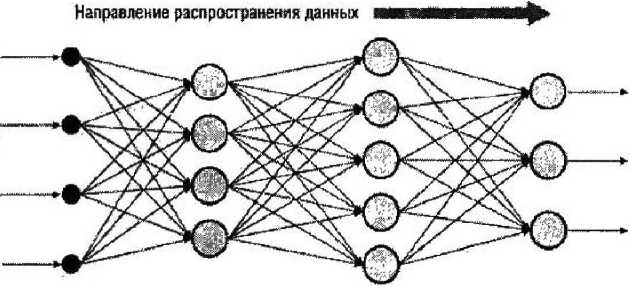
Направление ргспрйпраненмя ошибки

Рис. 2. Метод обратного распространения ошибки для многослойной полносвязанной нейронной сети

На рис. 3 проиллюстрирован метод градиентного спуска. К весовым коэффициентам применяется поправка, которая определяется в соответствии с формулой (2)

= (2)

где w - коэффициент синаптической связи между нейронами г и j слоя тг;

д - коэффициент скорости обучения сети;

Е - функция суммарной ошибки сети.

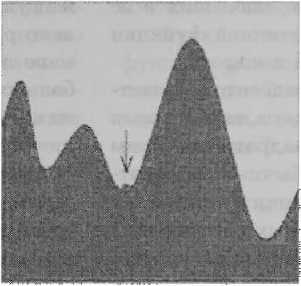
Рис. 3. Метод градиентного спуска при минимизации ошибки сети

При подобном обучении нейронной сети всегда существует возможность попадания алгоритма в локальный минимум. Для этого используются специальные приемы, позволяющие *выбить» найденное решение из локального экстремума. Данные методы изложены в работах [1; 3-4; 6-9]. Также одним из вариантов, помогающим в решении задачи определения глобального минимума па поверхности ошибок является сглаживание функции энергии. Показательно объяснить данное предположение па модели Хопфилда, описанной в работе [5].

Метод обратного распространения ошибки [6]. Метод обратного распространения ошибки - это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного персептрона и получения желаемого выхода.

Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Для возможности применения этого метода передаточная функция нейронов должна быть дифференцируема.

Для каждого узла определяется поправка, и это зависит от слоя, к которому относится узел. Кроме этого, на вход алгоритму нужно подавать структуру сети. Нейронные сети простой структуры (состоящие из двух уровней нейронов: скрытого и выходного) на практике дают хорошие результаты.

Недостатки алгоритма. Больше всего неприятностей приносит неопределенно долгий процесс обучения нейронной сети, при этом она может и не обучиться вовсе. Причины могут быть следующими:

• -    паралич сети. В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Большинство нейронов будут функционировать в области, где производная сжимающей функции очень мала;

• -    локальние минимумы,. Обратное распространение использует разновидность градиентного спуска - спуск вниз по поверхности ошибки, - непрерывно подстраивая веса в направлении к минимуму. Сеть может попасть в локальный минимум, когда рядом имеется гораздо более глубокий минимум;

• -    размер шага. Коррекции весов предполагаются бесконечно малыми. Это неосуществимо на практике, так как ведет к бесконечному времени обучения. Однако размер шага должен браться конечным.

Существует возможность переобучения сети. Весь набор образов, предоставленных к обучению, будет выучен сетью, но любые другие образы, даже очень похожие, могут быть классифицированы неверно.

Существуют современные алгоритмы второго порядка, такие как метод сопряженных градиентов и метод Левеиберга-Маркара, которые на многих задачах работают существенно быстрее (иногда на порядок). Разработаны также эвристические модификации этого алгоритма, хорошо работающие для определенных классов задач, - быстрое распространение и Дельта-дельта с чертой.

Метод сопряженных градиентов [3; 7]. Метод сопряжештых градиентов - метод нахождения локального минимума функции на основе информации о ее значениях и ее градиенте. В случае квадратичной функции в Нп минимум находится за п шагов.

Метод сопряженных градиентов является методом первого порядка, в то же время скорость его сходимости квадратична. Этим он выгодно отличается от обычных градиентных методов. При оптимизации функций общего вида метод сопряженных направлений сходится в 4-5 раз быстрее метода наискорейшего спуска. При этом не требуется трудоемких вычислений вторых частных производных в отличие от методов второго порядка.

Метод градиентного спуска с учетом моментов [1]. Идея метода заключается в добавлении к величине коррекции веса значения пропорционального величине предыдущего изменения этого же весового коэффициента. Величина коррекции веса рассчитывается согласно формуле (3)

Aw(t) = — р-—Н aAwtt - 1), (3)

где Aw(j) - значение коррекции веса на у-м шаге; р - длина шага; £(w) - функция ошибки; а - коэффициент инерции.

Быстрое распространение [9]. В методе быстрого распространения, или методе градиентного спуска с адаптивным обучением, производится пакетная обработка данных. Вычисляется усредненный градиент поверхности ошибок по всему обучающему множеству, и веса корректируются один раз в конце каждой эпохи.

Метод быстрого распространения действует в предположении, что поверхность ошибок является локально квадратичной. В этом предположении алгоритм быстрого распространения работает так:

• I.    На первой эпохе веса корректируются по тому же правилу, что и в методе обратного распространения, исходя из локального градиента и коэффициента скорости обучения.

• 2.    На последующих эпохах алгоритм использует предположение о квадратичности для более быстрого продвижения к точке минимума.

Исходные формульЕ метода быстрого распространения имеют ряд вычислительных недостатков. Во-первых, если поверхность ошибок не является вогнутой, алгоритм может уйти в ложном направлении. Далее, если вектор градиента не меняется или меняется мало, шаг алгоритма может оказаться очень большим и даже бесконечным. Наконец, если по ходу встретился нулевой градиент, изменение весов вообще прекратится.

Метод Дельта-дельта с чертой [8]. В некоторых случаях метод Дельта-дельта с чертой, или метод градиентного спуска с учетом моментов и адаптивным обучением, оказывается эффективнее, хотя в большей степени, чем метод обратного распространения, склонен застревать в локальных минимумах. Метод Дельта-дельта с чертой обычно довольно устойчив в отличие от метода обратного распространения.

В методе Дельта-дельта с чертой скорости обучения для отдельных весов корректируются на каждой эпохе таким образом, чтобы соблюдались следующие важные эвристические требования:

• —    начальная скорость обучения, используемая для всех весов на первой эпохе;

• -    коэффициент ускорения, который добавляется к скоростям обучения, когда производные не меняют знака;

• -    коэффициент замедления, на который умножаются скорости обучения в случае, когда производная меняет знак.

Применение линейного роста и экспоненциального убывания для скоростей обучения придает алгоритму большую устойчивость. Однако описанная схема может плохо рабо- тать на поверхностях ошибок, искаженных помехами, где при выраженном общем понижающемся рельефе производные могут резко менять знак. Поэтому при реализации алгоритма для увеличения или уменьшения скорости обучения берется сглаженный вариант производной.

Веса корректируются по тем же формулам, что и в методе обратного распространения, с той разницей, что коэффициент инерции не используется, а каждый вес имеет свою собственную, зависящую от времени скорость обучения. Вначале всем скоростям обучения присваиваются одинаковые стартовые значения, затем на каждой эпохе они корректируются.

Модель Хоп филда [4]. Модель Дж. Хопфилда представляет собой сеть связанных между собой нейронов, каждый из которых характеризуется своим состоянием -уровнем возбуждения х^. Состояние любого нейрона в каждый момент времени t сигмоидально зависит от взвешенной суммы сигналов, поступающих к нему от других нейронов: