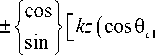Анализ интерференции радиально-поляризованных лазерных пучков, сформированных кольцевыми оптическими элементами с вихревой фазой в условиях острой фокусировки

В задачах оптического захвата и манипулирования, микроскопии и записи данных [1 –3] является актуальной возможность формирования заданных трёхмерных распределений интенсивности. При этом важно обеспечить локализацию лазерного излучения в минимально возможном объёме.

Для уменьшения поперечного размера фокального пятна используется острая фокусировка с применением высокоапертурных объективов. Однако продольный размер фокального пятна даже в предельном случае оказывается в два раза больше поперечного [4].

Дополнительная аподизация зрачка фокусирующей системы для цилиндрических типов поляризации (радиальной и азимутальной) позволяет свести векторную задачу к практически скалярной и преодолеть дифракционный предел, предсказанный скалярной теорией [5 – 12]. Однако, как правило, в этих случаях уменьшение поперечного размера фокального пятна сопровождается ещё большим увеличением его продольного размера.

Для обеспечения одновременной локализации лазерного излучения в различных направлениях (т.е. в объёме) были предложены различные способы, в большинстве своём основанные на эффекте интерференции. Хорошо известны методы встречной интерференции остросфокусированных пучков [4, 13 – 19] и интерференции пучков, сформированных различными зонами оптического элемента, дополняющего высокоапертурный объектив [20–22].

В данной работе рассматривается второй способ, основанный на дифракции падающего излучения на

двух кольцевых апертурах, наложенных на зрачок фокусирующей системы. При этом в каждое кольцо может быть внесена дополнительная фазовая аподизация.

Как правило, используется постоянный набег фазы [20 – 22]. Однако в работах [23 –25] было показано, что использование вихревой фазовой аподизации острофокусирующей системы позволяет эффективно управлять распределением векторного поля в фокальной области для различных типов поляризации. В связи с широким спектром приложений [26] особый интерес представляет радиальная поляризация. Поэтому в данной работе выполнены более общие исследования по использованию вихревой фазовой функции для формирования и управления трёхмерной структурой сфокусированного радиально-поляризованного излучения.

1. Модель острой фокусировки

Электрическое поле в фокальной области при острой фокусировке радиально-поляризованного излучения можно представить в следующем виде:

а 2п

^ cos ф cos 9 ‘

• г а 2п                                ¹

E rad ( р , ф , z ) = - if- f f B ( 9 , ф)Т ( 9 ) sin ф cos 9 ^

V

-

sin 9 ,

x

x exp [ ik ( p sin 9 cos( ф - ф ) + z cos 9 ) ] sin 9 d 9 d ф , где ( p , ф , z) - цилиндрические координаты в фокальной области, ( 9 , ф ) - сферические угловые координаты выходного зрачка фокусирующей системы, а -максимальное значение угла 9 , связанное с числовой апертурой системы, B ( 9 , ф ) - функция пропускания,

T ( 9 ) - функция аподизации зрачка (для апланатиче-

ских систем T ( 9 ) = Vcos 9 ), k = 2 п / X - волновое

число, X - длина волны, f - фокусное расстояние.

Для вихревых полей B ( 9,ф ) = R ( 9 ) exp ( im ф ) выражение (1) можно свести к выражению с одинарным интегрированием [23 – 25]:

e rad ( р , _Ф , z ) =- ikf х

x j R ( 9 ) T ( 9 )Q rad ( р , ф , 9 ) sin 9 exp ( ikz cos 9 ) d 9 , 0

• m im Ф где Q rad (р, Ф, 9) = —— x

x

i [ J m ₊ 1 ( k P sin 9 ) - J_m -1 ( k P sin 9 ) ] cos 9 [ J_{m +} 1 ( k P sin 9 ) + J_m -1 ( k P sin 9 ) ] cos 9 - 2 J_m ( k р sin 9 ) sin 9

2. Анализ фокального распределения для одного кольца

При острой фокусировке пучков с радиальной поляризацией введение узкой кольцевой диафрагмы, блокирующей излучение практически во всей центральной части линзы [5, 9, 27], является простым, хотя и энергетически затратным способом формирования узких протяжённых пучков в фокальной области. В случае радиальной поляризации формируется тонкая световая нить, поперечный размер которой соответствует скалярному дифракционному пределу. При других типах поляризации фокальное пятно (или кольцо) оказывается большего размера из-за вклада в фокальную область различных компонент электромагнитного поля.

Заметим, что, как правило, рассматривается интенсивность формируемого поля на оптической оси или в фокальной плоскости. В данной работе нас интересует трёхмерное распределение в фокальной области. Иллюстрация рассматриваемой системы показана на рис. 1.

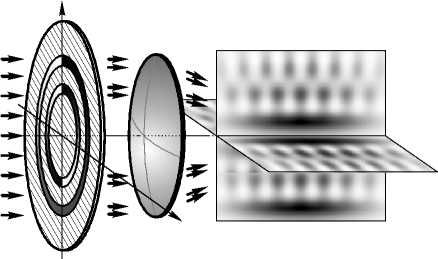
Рис. 1. Иллюстрация формирования трёхмерной картины

в фокальной области на основе интерференции пучков от узких кольцевых апертур с различной вихревой фазой

Прежде чем решать поставленную задачу анализа интерференции пучков от узких кольцевых апертур с различной вихревой фазой, выполним детальный анализ поля, формируемого одним кольцом.

Используя выражения (2) и (3), рассмотрим электрическое поле в фокальной области при использова-

нии равномерно освещённой узкой кольцевой апер туры, ограниченной азимутальными углами 91 и 92:

e rad ( р , ф , z ) =- ikf х

9                .------                                   (4)

x J Q ra ( р , Ф , 9 )Vcos 9 sin 9 exp( ikz cos 9 )d 9 .

2.1. Отсутствие вихревой фазы (m = 0)

Для радиальной поляризации наиболее интересным является случай отсутствия вихревой фазы ( m =0). В этом случае интенсивности цилиндрических компонент электрического поля в фокальной области можно приближённо записать в следующем виде:

| E x ⁽ р , Ф , z )| ² ~ ^A 2 cos ^{3 9} c sin ^{2 9} c J ² ( k р sin ⁹ c ) ,

I Е^О Ф ( р , Ф , z )p = 0,                                (5)

|Emad o, z ⁽ р , Ф , z )| ² ® ^{A 2} cos ⁹ c sin ^{4 9} c J ² ( ^k р sin ⁹ c ) ,

где A = 9 2 - 9 ₁ - угловая ширина кольцевой апертуры, 9 _c = ( 9 ₁ + 9 2 )/2 - угол, соответствующий центру кольцевой апертуры.

Полная интенсивность:

| e a= о ( р , ф , z )|² *

A ² cos 9 _c sin ² 9 _c x

x [ cos ² 9 _c J ² ( k р sin 9 _c ) + sin ² 9 _c J ₀ ² ( k р sin 9 _c ) ] .

Как следует из выражений (5) и (6), в приближении узкой кольцевой апертуры поле в фокальной области не меняется вдоль оптической оси и является осесимметричным (не зависит от полярного угла).

Формула (6) наглядно показывает, что в зависимости от радиуса кольцевой апертуры на оптической оси будет формироваться различное распределение интенсивности. В частности, при малых радиусах 9 _c ^0 более мощным будет вклад функции Бесселя первого порядка, и будет формироваться полая световая трубка. При больших радиусах 9 _c ^90° более мощным будет вклад функции Бесселя нулевого порядка, и будет формироваться тонкая световая игла. Однако для получения количественных оценок формула (6) неудобна, поэтому придётся использовать её приближения. Их можно получить в двух случаях: вблизи оптической оси и вдали от неё (при средних значениях оба приближения будут грубыми).

При небольших расстояниях от оптической оси функции Бесселя заменяем их разложениями в ряд Тейлора. После преобразований получим

| E mad о⁽ р , Ф , z )| ² ~ ^A 2 cos ⁹ c sin ^{4 9} c ^x

x

1 - ⁽^р) ( 2sin ² 9 _c - cos ² 9 _c ) +

+ ^{( k р )} sin ² 9 (3sin ² 9 - 2cos ² 9 ) 32 ^{c c c}

Анализируя выражение (7), можно вынести следующие заключения.

Максимальное значение интенсивности на оси соответствует максимуму величины cos 9 _c sin⁴ 9 _c и будет достигнуто при 9 _c = arccos(1/ V5) = 63,43 ° .

Если ограничиться слагаемым второй степени, то получаем, что переход от минимума на оси к максимуму произойдёт при обращении этого слагаемого в нуль - при 9 _c = arctg(1/V2) = 35,3 ° . В этом случае вершина будет плоской, а так как слагаемое четвёртой степени при этом отрицательно , то будет плоский максимум.

В случае наличия максимума, если он не очень близок к плоскому (пренебрегаем слагаемым 4-й степени), радиус первого тёмного кольца равен

• p 2  =__________ 4__________

• ™” к ² ( 2 sin ² 9 _c - cos ² 9 _c )

При плоском максимуме радиус тёмного кольца

= ^288 / к .

Равен P min

Если учесть слагаемое 4-й степени, то получим, что экстремум выражения в квадратных скобках в (7)

достигается при

^{( к} P^{) 2} =

4 ( 2sin ² 9 _c - cos ² 9 _c ) sin ² 9 _c ( 3 sin ² 9 _c - 2 cos ² 9 _c )

если дробь положительна. Последнее требование выполняется при 9 _c <35,3 ° или при 9 _c >arctg(V2/3) = 39,23 ° .

В первом случае получим радиус первого светлого кольца (при минимуме на оси), а во втором – уточнённое значение радиуса тёмного кольца.

Заметим, что при 9c ^ 90° размер светового пятна на оптической оси будет уменьшаться до значения pmin = 2 / к2, но при этом также будет уменьшаться энергия в нём, т.к. имеется множитель cos 9c.

Анализ асимптотического поведения для поля (6) при больших значениях радиуса на основе замены функций Бесселя их асимптотическими выражениями:

I e ra= o ( p , ф , z )|² «a ²

sin 29r

------- x

2 п к p

x [ 1 - cos 2 9 _c sin ( 2 к p sin 9 _c ) ]

показывает, что на периферии поле имеет явно выраженные осцилляции – набор концентрических колец. Исключением является случай, когда 9 _c = 45° и выражение в квадратных скобках становится постоянным, т.е. периферийные кольца исчезают.

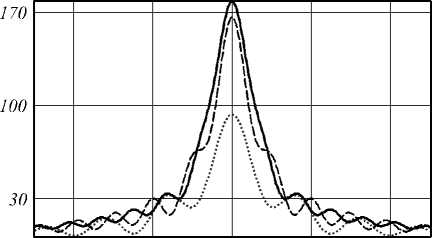
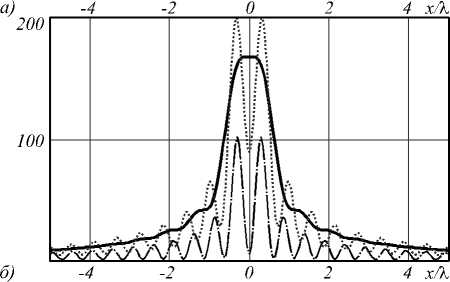
В табл. 1 и на рис. 2 приведены иллюстрации для рассмотренных выше случаев. Также в таблице приве- дены размеры светового пятна или кольца по уровню полуспада от максимального значения (FWHM), а также соответствующий радиус до ближайшего минимума.

Из результатов расчётов видно, что, действительно, при 9 _c = 35,3° формируется световое пятно с плоской вершиной, при 9 c = 45° в периферийной области отсутствуют осцилляции (кольца), а при 9 _c = 63,43° достигается максимальное значение интенсивности в фокальном пятне.

а)

б)

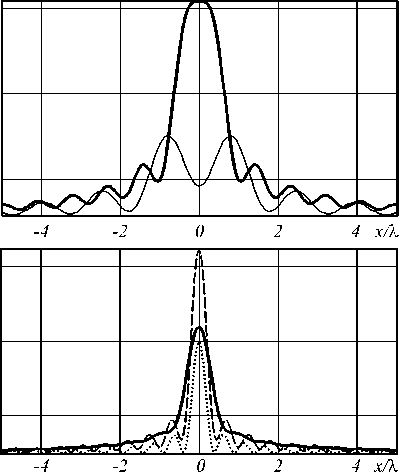
Рис. 2. Сечение интенсивности в фокальной плоскости для радиально-поляризованного пучка без вихревой фазы (m=0) при 0 _c=2O° (тонкаялиния) и 0 _c=35,3° (толстая линия) (а), а также при 0 _c=45° (толстая линия),

0 _c=63,43° (пунктирная линия) и 0 _c=8O° (точечная линия) (б)

• 2.2. Наличие вихревой фазы первого порядка (m = 1)

При наличии вихревой фазы первого порядка ( m = 1) при фокусировке радиально-поляризованного поля на оптической оси также будет иметь место ненулевая интенсивность. В этом случае интенсивности цилиндрических компонент электрического поля в фокальной области можно приближённо записать в следующем виде:

I E^p ( P , Ф , z )| ² « 0,25 A ² cos ³ 9 c sin ² 9 c x

x[ J 0 ( к p sin 9 _c ) - J ₂ ( к p sin 9 _c ) ] 2 ,

I е;1 ф ( p , Ф , z ) 2 « 0,25 A ² cos ³ 9 c sin ² 9 c x           (9)

x[ J ₀ ( к p sin 9 _c ) + J ₂ ( к p sin 9 _c ) ] 2 ,

I E md _z ⁽ p , Ф , ^z )| ² «^A 2 cos ⁹ c sin ^{4 9} c J ( ^к p sin ⁹ c ) .

Полная интенсивность:

IEma=1 (p, Ф, z)2 « 0,25A2 cos 9c sin2 9c x x{2cos2 9c [ J0 (кpsin 9c) + J22 (кpsin 9c)]+ (10) +4sin2 9cJ2 (кpsin 9c)}.

Из формулы (10) очевидно, что при малых радиусах кольцевой апертуры ( 9 _c ^ 0) более мощным будет вклад функции Бесселя нулевого порядка, и будет формироваться протяжённый световой стержень.

При больших радиусах кольцевой апертуры ( 9 _c ^ 90°) более мощным будет вклад функции Бесселя первого порядка, и будет формироваться тонкая полая световая трубка. То есть ситуация противоположна случаю без вихря (см. (6)).

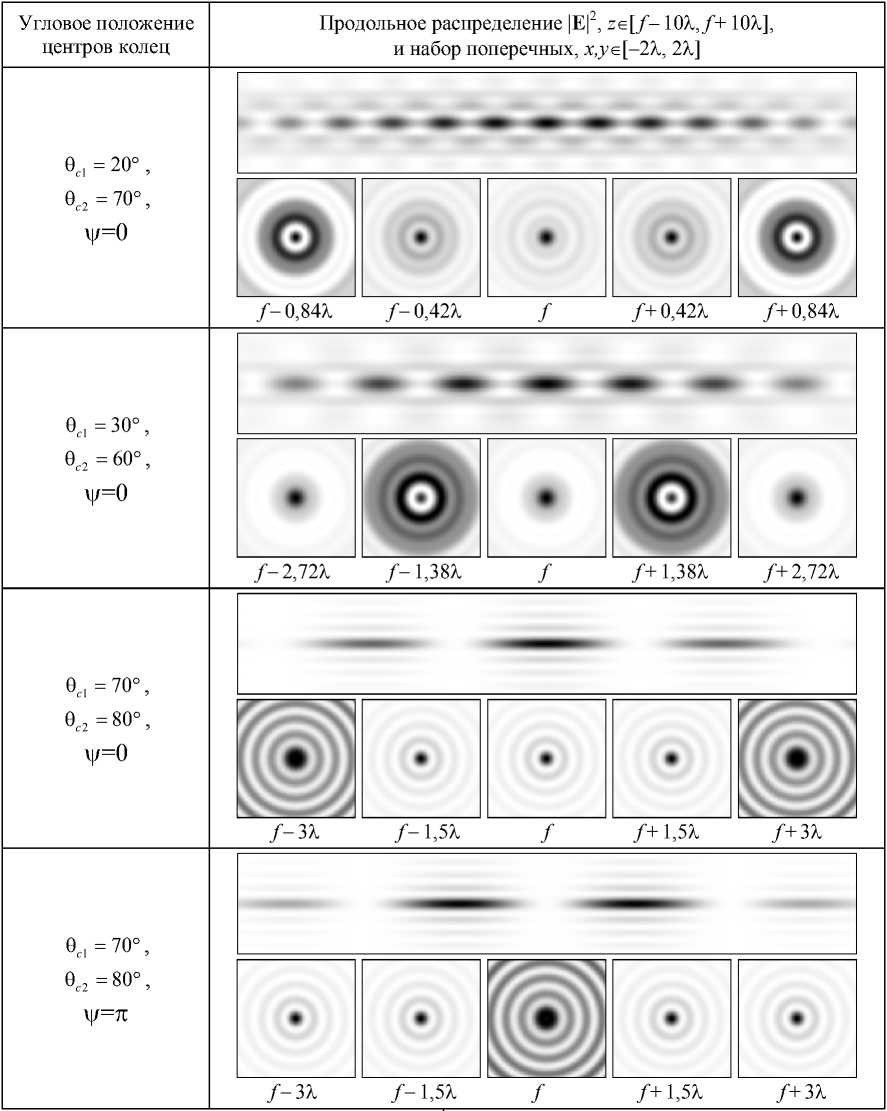
Табл. 1. Распределение интенсивности (негатив) для радиально-поляризованного пучка без вихревой фазы (m=0) при одной кольцевой диафрагме шириной Д =4° с различным угловым положением центра

При небольших расстояниях от оптической оси функции Бесселя в (10) заменяем их разложениями в ряд Тейлора. После преобразований получим

|E ™d i ( Р , Ф , z )| 2 ~ 0,25 А ² cos 9 _с sin ² 9 c х

х

— cos ² 9_С - ⁽ ^^Р) sin ² 9_С (cos ² 9_С - sin ² 9_С) + 2 ^c 4 ^{c c c}

В этом случае вершина будет плоской, а так как слагаемое четвёртой степени при этом отрицательно , то будет плоский максимум. В случае наличия максимума, если он не очень близок к плоскому (пренебрегаем слагаемым 4-й степени), радиус первого тёмного кольца равен p min = 2ctg 2 9 _c / ( k 2 (cos² 9 _c - sin ² 9 _c )). При

плоском максимуме радиус тёмного кольца равен

+ ⁽ k ^{р )} sin 4 9 ^cos ² 9 128 ^{c c}

- 8sin ² 9 _c )

p min = 4Z k . Если учесть слагаемое 4-й степени, то получим, что экстремум выражения в квадратных скобках в (11) достигается при

Подобно случаю без вихря, анализируя выражение (11), можно вынести следующие заключения. Максимальное значение интенсивности на оси соответствует максимуму величины cos³ 9 _c sin² 9 _c и будет достигнуто при 9 _c = arccos(V3/ 5) = 39,23 ° . Если ограничиться слагаемым второй степени, то получаем, что переход от максимума на оси к минимуму произойдёт при обращении этого слагаемого в нуль - при 9 _c = 45°.

^{( k} Р^{) 2} =

16 ( cos ² 9 _c - sin ² 9 _c ) sin ² 9 _c ( 7cos ² 9 _c - 8sin ² 9 _c )

если дробь положительна. Последнее требование выполняется при 9c

9_c >45°. Во втором случае получим радиус первого светлого кольца (при минимуме на оси), а в первом – уточнённое значение радиуса тёмного кольца.

При использовании выражения для радиуса тёмного кольца ρ2min = 2ctg2θc / (k2 (cos2 θc - sin2 θc)) можно доказать, что размер светового пятна на оптической оси будет наименьшим при sin2 9 c = 1 - 72/2 ~ 9 c = 32,77° и равен ρ2min =(6+4 2)/k2 .

В отличие от случая без вихря, моделирование (см. рис. 3 и табл. 2) показало, что здесь есть одна особенность – при минимуме в центре максимальное значение интенсивности в кольце может оказаться больше, чем значение максимума в центре. Найдём угол, при котором кольцо имеет наибольшую интенсивность. Используя формулу (11) и выражение для позиции экстремума, получим, что необходимо найти макси- мум выражения

4-8cos²θ_c + cos⁴θ_c 8-15cos²θ_c

⋅ cos θ_c sin²θ_c

в области 45°< θc< 90°. Аналитически это невозможно сделать точно, но можно убедиться, что дробь в этом диапазоне углов имеет почти постоянное значение. Поэтому с достаточной точностью можно ограничиться нахождением максимума величины cos θ_c sin²θ_c , который достигается при θ_c = arccos( 1/3) = 54, 73° .

Несмотря на заметное отличие исходных выражений (6) и (10), асимптотическое поведение очень похоже на предыдущий случай:

Табл. 2. Распределение интенсивности (негатив) для радиально-поляризованного пучка при наличии вихревой фазы первого порядка (m=1) при одной кольцевой диафрагме шириной Δ=4° с различным угловым положением центра

IEmdi(p, Ф, z)2 * A sin 2⁹ х 2n kp

x[1 + cos 29c sin (2kp sin 9_c)],

т.е. отсутствие периферийных колец при 9c = 45°.

В данном разделе проводится анализ интерференции радиально-поляризованных лазерных пучков, сформированных кольцевыми оптическими элементами с вихревой фазой в фокальной области острофо-кусирующей системы.

В фокальной области поле от двух кольцевых диафрагм, освещённых радиально-поляризованным излучением, можно описать как суперпозицию двух пучков вида (4):

Eradn, (p, ф, z) = Erm (p, ф, z) + exp (i ф) E 2^ad (p, Ф, z) =

- ikf j Qrad (p, Ф, 9)Vcos 9 sin 9 exp (ikz cos 9) d9

- ikf exp (i ф)х

^^^^^^B

Рис. 3. Сечение интенсивности в фокальной плоскости для радиально-поляризованного пучка при наличии вихревой фазы первого порядка (m=1) при 0c=2O° (точечная линия), 0c=32,7° (пунктирная линия) и 0c=39,23° (чёрнаялиния) (а), а также при 0c=45° (чёрная линия), 0c=6O° (точечная линия) и 0c=8O° (штрихпунктирная линия) (б)

64                       ________ xj Qa (p, Ф, 9)Vcos 9 sin 9 exp (ikz cos 9) d9,

9з

где ф - постоянная, соответствующая разности фаз в первом и втором кольцах.

Если в (13) порядки вихревой фазы в каждом из колец равны (m = n), то интерференция двух пучков останется осесимметричной.

При радиальной поляризации в отсутствие вихревой фазы (m = n =0) интенсивность для выражения (13) принимает следующий конкретный вид:

|Erad0,n=0(p, Ф, z)|2 * A2 cos 9c 1 sin2 9c 1 X x^cos2 9c 1 Ji (kpsin 9c 1) + sin2 9c 1 J02 (kpsin 9c 1)] +

+A2 cos 9_c2 sin²9_c2x

x^cos²9 _{c 2}J²(kpsin 9 _c2) + sin²9 _c2J₀²(kpsin 9 _c2)] +

Как видно из приведённых результатов моделирования, они полностью подтверждают аналитические предположения. Заметная погрешность имеется только при определении угла максимизации интенсивности кольца (вместо теоретического значения 55° оказалось 60°).

+2A₁A2cos [kz (cos 9_{c 1}- cos 9_c2)-ф]х

3. Анализ фокального распределения для двух колец с одинаковой вихревой фазой

При использовании двух узких кольцевых апертур в выходном зрачке острофокусирующей системы в фокальной области формируются два векторных пучка Бесселевого типа [28, 29] различного масштаба. Если дополнительно внести вихревые фазы в освещающий пучок так, чтобы кольцевые апертуры имели разные фазы, то получаемые пучки Бесселя будут также иметь разный порядок. Их интерференция приводит к созданию определённого трёхмерного распределения интенсивности. Ранее исследование интерференции Бесселевых пучков выполнялось в скалярном случае [30-32].

x^cos 9_{c 1} cos 9_c2 sin 9_{c 1} sin 9_c2х

x[cos9_{c 1} cos9_c2J, (kpsin9_{c 1}) J, (kpsin9_c2) + + sin 9 _{c 1} sin 9 _{c 2}J0 (kp sin 9 _{c 1}) J0 (kp sin 9 _{c 2})], где Δ1, Δ2 – угловые ширины, θc1, θc2 – угловые центральные радиусы первой и второй кольцевой апертур соответственно.

Как видно из (14), теперь имеется зависимость поперечного поля от расстояния z, хотя осевая симметрия (отсутствие зависимости от полярного угла ф) сохраняется. Постоянная разность фаз между кольцами ф фактически влияет только на смещение всей трёхмерной картины в фокальной области вдоль оптической оси.

Выражение (14) довольно громоздкое, поэтому для анализа воспользуемся асимптотическим приближением на некотором удалении от оптической оси:

IE rad о „ n (p, Ф, z )| * A²sn^c- й — cos29_r. sin (2 kp sin 9_H)! + A 2 sn^c. Г1 — cos29_{r 2} sin (2 kp sin 9_r2)! +

I  m=0,n=^о^,ж,          ¹  2_Лkp  ^{[            c 1     ( p      c 1})J     ²  2nkp  ^{[            c2    (           c2 )J}

+2A₁A₂ cos Гkz (cos 9_{c 1}

sin29 , sin29 ₂

^-cos ⁹_c 2)^- ф] -----c¹------c-^X

2n kp

^X{^cos(⁹c 1 -⁹c 2 ) ^cos[ ^k p(^{sin 9}c 1 - ^{sin 9}c 2 )]-^cos(⁹c 1 ⁺⁹c 2 ) ^sin[ ^k p(^{sin 9}c 1 ^{+ sin 9}c 2 )]}^.

При наличии одинаковой вихревой фазы в обоих кольцах выражения в фокальной области будут аналогичными (14) и (15) с точки зрения зависимости от расстояния и наличия осевой симметрии. Во всех случаях будет множитель cos[kz (cos 9c 1 - cos 9_c2) -ф], причём

он не зависит от порядка вихря. Осевая симметрия объясняется тем, что зависящие от полярного угла множители в (3) равны для обоих колец и их можно вынести за скобку, как для одного кольца.

В частности, при вихревой фазе первого порядка (m = n = 1) получим асимптотическое приближение:

| e r:__1, n=m ф, z )|²«

Как следует из приведённых результатов, несмотря на периодические изменения, поперечное распределение в этом случае остаётся осесимметричным.

Более сложные распределения можно получить, если использовать различные вихревые фазы в каждом из колец [33]. Рассмотрим получаемые распределения для различных пар фазовых набегов.

«А2

sin 29 _c 1 2n kp

[1 + cos 29 _c 1

sin (2 kp sin 9 _c 1)] +

+А2  ----^2-[1 + cos 29_c2sin (2kp sin 9_c2)] +

2n kp

+A1A ₂cos [ kz (cos 9 _c 1 - cos 9 _{c 2})-y]x

J sin 29 _c 1 sin 29 _{c 2}

x -----------------x n k p

• ^x{^cos(⁹c 1 ^-9c 2 ) cos ^[k p(^{sin 9}c 1 ^- sin ⁹c 2 )] +

• ⁺ cos (⁹c 1 +⁹c 2 ) ^{sin [}к p(^{sin 9}c 1 + ^{sin 9}c 2 )]}.

4. Анализ фокального распределения для двух колец с различной вихревой фазой

Если в (13) порядки вихревой фазы в каждом из колец различные, то интерференция двух пучков перестанет быть осесимметричной. Структура формул в общем останется похожей, но изменится множитель, зависящий от расстояния: в нём появится зависимость от полярного угла.

В частном случае при радиальной поляризации с порядками вихревой фазы (m =0, n = 1) интенсивность для выражения (13) принимает следующий конкретный вид:

I^Em=0,n=1⁽p, Ф, z)|² » ^A2 ^{cos 9}c 1 sin^{2 9}c 1 ^x

x[cos² 9_c 1 J1²(kpsin 9_c 1) + sin² 9_c 1 J0 (kpsin 9_c 1)] +

Выражения (15) и (16) очень похожи, поэтому рассмотрим их сразу оба. В фигурных скобках имеются периодические функции от радиуса, которые вместе с

множителем, зависящим от расстояния, создают картину максимумов, расположенных на прямых, параллельных прямым sin 9,- sin 92

z = ±p-----------— (первая серия)

cos 9c 1 - cos 9c₂

+0,5 А2 cos 9_c2sin² 9_c2x

x[cos² 9_c2(J₀²(kpsin 9_c2) + J₂²(kpsin 9_c2)) +

+ 2sin² 9_c2J1²(kp sin 9_c2)] +

+2А1А 2 sin [ kz (cos 9 c 1 - cos 9 c2 )-ф- y]x x, I cos 9,. cos 9 2 sin 9 .sin 9 , x c1          c 2         c1         c 2

x[sin9_c 1 sin9_c2J0 (kpsin9_c 1) J1 (kpsin9_c2)-

и sin 9,+ sin 92

z = ±p-----------— (вторая серия). cos 9c 1 - cos 9c₂

Если будет выполнено условие cos (9c 1 +9c₂) = 0, то вторая серия исчезает, а линии первой серии будут параллельны прямым z = ±p. Первая серия всегда

-0,5cos9_c 1 cos9_c2J1 (kpsin9_c 1 )x x( J0 (kp sin 9_c2)- J₂(kp sin 9_c2))

где A1, А2 - угловые ширины, 9_c1, 9_c2- угловые центральные радиусы первой и второй кольцевой апер-

тур соответственно.

В случае произвольных порядков вихревой фазы зависимость от полярного угла (как следует из (3))

сохраняется.

Анализ выражения (14) и аналогичного ему для (m = n = 1) при малом расстоянии от оси не проводим, так как принципиально он не отличается от анализа одного кольца в разделе 2.

Примеры распределения интенсивности приведены в табл. 3 и 4.

|^Erad0,n=1⁽p, Ф,^z)|2 « ^A2^{cos 9}c 1 ^sin4 ⁹c 1

+A2 cos 9_c2sin² 9_c2

определяется множителем

- cos 9c₂)- (n - m)ф-ф] -

радиальная симметрия меняется на поворотную.

Примеры расчётов для различных сочетаний порядков вихревых фаз приведены в табл. 5 и 6.

При небольшом расстоянии от оптической оси используем разложение в ряд Тейлора. Получим выражение

1 - ⁽k^p) / 2 sin² 9.. - cos² 9.,)+⁽k^p) sin² 9.. (3sin² 9.. - 2cos² 9.J ₄                  c1              c1        ₃₂            c1              c1                c1

1cos² 9 ₂ - ⁽k^p) sin² 9 ₂ (cos² 9 ₂ - sin² 9 ₂)+ ⁽k^p) sin⁴ 9 ₂ (7cos² 9 ₂ - 8sin² 9 ₂) ₂         c2      ₄           c2          c2           c2      128          c2            c2             c2

+2A1A₂sin [kz (cos 9_c 1

- cos 9_c2) - ф - ф] д/cos 9_c 1 cos 9_c2sin² 9_c 1 sin 9_c2

kp

— x

x

(sin²9_c2 -0,5cos9_C, cos9_c2)-⁽k^p) (sin² 9_c2 (2sin² 9_C1

c 2                    c1          c 2          ₈                 c 2                c1

+ sin² 9_c2) - 0,5 cos 9_c 1 cos 9_c2(sin² 9_c 1 + 3sin² 9_c2))

Табл. 3. Распределение интенсивности (негатив) для радиально-поляризованного пучка без вихревой фазы (m=n=0) при двух кольцевых диафрагмах шириной Д1=Д2=4° с различным угловым положением центра

Несмотря на громоздкость выражения, попытаемся получить из него какие-нибудь результаты. Анализируя перекрёстное слагаемое, получим, что амплитуду зависимости от расстояния и полярного угла вблизи оси можно ослабить, если обратить в нуль слагаемое первой степени. Это происходит при выполнении равенства cos 9c 1 = 2 sin2 9c2 / cos 9c2. Так как косинус не превосходит единицы, такое равенство возможно при условии cos9c2>(V17 -1)/4 ~ 9c2 < 38,67°. При этом угол 9 c 1 может быть как меньше угла 9c2 (если 9c2 > 35,26°), так и больше. Например, при 9c2 = 20° 9c1 = 75,58°, при 9c2 = 30° 9ci = 54,74°, при 9с2 = 37° 9с 1 = 24,9°.

Наоборот, если анализировать только «неперекрёстные» слагаемые, то явные аналитические выводы можно получить лишь в случае А1 = А₂. Тогда, используя результаты, полученные для отдельных колец, можно утверждать следующее. Наибольшее значение на оси будет при 9_c1 = 63,43° 9_c2= 39,23°, достаточное условие максимума в нуле: 9_c 1 > 35,26° & 9_c2< 45° ; достаточное условие минимума в нуле: 9_c 1 < 35,26° & 9_c2> 45° .

Табл. 4. Распределение интенсивности для двух кольцевых диафрагм шириной А1=А2=4° с угловыми положениями центров

Условие плоской вершины однозначно определяет один из углов, если задан другой, но требует численного решения. Несколько упрощается решение в частном случае, когда cos 9c 1 sin 9_c 1 = cos 9_c2 sin 9_c2 ~ 9_c 1 +9_c2 = 90°, так как сокращается общий множитель. В этом случае плоская вершина получается при угле 9c1, удовлетворяющем уравнению: 2tg59_c 1 - tg³9_c 1 + tg²9_c 1 -1 = 0, которое имеет корень tg 9_c 1 « 0,85 ~ 9_c1 = 40,36°; 9_c2=49,64°. При этом неочевидно, будет ли при этом плоский максимум или плоский минимум.

Асимптотическое приближение приводить не будем, так как в области, когда оно верно, интенсивность мала и её изменение сложно наблюдать визуально.

Заключение

В работе получены аналитические выражения для поля в фокальной области для радиально-поляризованного пучка при наличии одной и двух кольцевых апертур. Асимптотические выражения выписаны для поля на некотором удалении от оптической оси.

Для одной узкой кольцевой апертуры с вихревой фазой фокальное распределение пропорционально суперпозиции функций Бесселя различного порядка. При этом поле обладает осевой симметрией и не зависит от продольной координаты.

Проанализирована зависимость структуры формируемого поля от радиуса кольцевой апертуры. При отсутствии вихревой фазы при малых радиусах более мощным будет вклад функции Бесселя первого порядка, и будет формироваться полая световая трубка. При больших радиусах более мощным будет вклад функции Бесселя нулевого порядка, и будет формироваться тонкая световая игла. Паритет достигается при угловом радиусе кольцевой апертуры 9c = 35,3°. В этом случае вершина светового пятна в каждой плоскости будет плоской. При увеличении радиуса кольца размер светового пятна на оптической оси будет уменьшаться, но при стремлении к предельной величине (9c ^ 90°) также будет уменьшаться энергия в нём. Максимальное значение интенсивности имеет место при 9c = 63, 43° .

При наличии вихревой фазы первого порядка, наоборот, при малых угловых радиусах кольцевой апертуры будет формироваться световой стержень, а при больших – полая световая трубка. Максимальное значение интенсивности на оси достигается при 9c = 39,23°. Переход от полой трубки к стержню происходит при 9c = 45°. В этом случае вершина будет плоской, это будет плоский максимум. Размер светового пятна на оптической оси будет наименьшим при 9c = 32,77°.

При использовании двух узких кольцевых апертур в выходном зрачке острофокусирующей системы в фокальной области формируются два векторных пучка Бесселевого типа различного масштаба. В случае одинаковой вихревой фазы в обоих кольцах поле в фокальной области остаётся осесимметричным, но появляется периодическая зависимость от продольной координаты за счёт интерференции пучков от каждого из колец. При этом частота периодических изменений пропорциональна разности косинусов центральных углов кольцевых апертур.

Если в каждом из колец имеются вихревые фазы различного порядка, то получается интерференция более сложного типа, которая приводит к формированию поступательно-вращающихся пучков. Скорость вращения пропорциональна разности порядков вихревой фазы. Таким образом, управлять трёхмерной структурой в фокальной области можно как за счёт положения колец, так и за счёт фазового распределения в каждом из колец. Такой подход расширяет возможности оптического захвата и манипулирования микрочастицами.

Табл. 5. Распределение интенсивности (негатив) для радиально-поляризованного пучка для двух кольцевых диафрагм шириной Д1=Д2=4° с различными угловыми положениями центров при наличии в кольцах вихревой фазы первого и нулевого порядка

Табл. 6. Распределение интенсивности (негатив) для радиально-поляризованного пучка для двух кольцевых диафрагм шириной Δ₁=Δ₂=4° с угловыми положениями центров θ_c1=30° и θ_c2=60° при наличии в кольцах вихревой фазы разного порядка

• 2.    Martínez-Corral, M. The resolution challenge in 3D optical microscopy / M. Martínez-Corral and G. Saavedra // Progress in Optics. – 2009. – Vol. 53. – P. 1-67.

• 3.    Walker, E. Toward terabyte two-photon 3D disk / E. Walker, A. Dvornikov, K. Coblentz, S. Esener and P. Rent-zepis // Optics Express. – 2007. – Vol. 15. – Р. 1226412276.

• 4.    Хонина, С.Н. Формирование световых шаров на основе встречной интерференции остросфокусированных пучков с различной поляризацией / С.Н. Хонина, А.В. Устинов // Вестник Самарского государственного аэрокосмического университета им. академика С.П. Королёва (национального исследовательского университета). – 2013. – № 2(40). – С. 208-224.

• 5.    Dorn, R. Sharper focus for a radially polarized light beam / R. Dorn, S. Quabis and G. Leuchs // Physical Review Letters. – 2003. – Vol. 91. – P. 233901.

• 6.    Davidson, N. High-numerical-aperture focusing of radially polarized doughnut beams with a parabolic mirror and a flat diffractive lens / N. Davidson and N. Bokor // Optics Letters. – 2004. – Vol. 29. – P. 1318-1320.

• 7.    Kalosha, V.P. Toward the subdiffraction focusing limit of optical superresolution / V.P. Kalosha and I. Golub // Optics Letters. – 2007. – Vol. 32. – P. 3540-3542.

• 8.    Kozawa, Y. Sharper focal spot formed by higher-order radially polarized laser beams / Y. Kozawa and S. Sato // Journal of Optical Society of America A. – 2007. – Vol. 24. – P. 1793.

• 9.    Khonina, S.N. Sharper focal spot for a radially polarized beam using ring aperture with phase jump / S.N. Khonina and A.V. Ustinov // Journal of Engineering. – 2013. – ID 512971.

• 10.    Хонина, С.Н. Исследование применения аксиконов в высокоапертурной фокусирующей системе / С.Н. Хони-на, С.Г. Волотовский // Компьютерная Оптика. – 2010. – Т. 34, № 1. – С. 35-51.

• 11.    Khonina, S.N. Reduction of the focal spot size in high-aperture focusing systems at inserting of aberrations / S.N. Khonina and E.A. Pelevina // Optical Memory and Neural Networks (Information Optics), Allerton Press. – 2011. – Vol. 20(3). – P. 155-167.

• 12.    Khonina, S.N. Simple phase optical elements for narrowing of a focal spot in high-numerical-aperture conditions / S.N. Khonina // Optical Engineering. – 2013. – Vol. 52, Issue 9. – P. 091711.

• 13.    Hell, S. Fundamental improvement of resolution with a 4Pi-confocal fluorescence microscope using two-photon excitation / S. Hell and E.H.K. Stelzer // Optics Communications. – 1992. – Vol. 93. – P. 277-282.

• 14.    Bokor, N. Toward a spherical spot distribution with 4p focusing of radially polarized light / N. Bokor, N. Davidson // Optics Letters. – 2004. – Vol. 29, Issue 17. – P. 1968-1970.

• 15.    Sandeau, N. Arrangement of a 4Pi microscope for reducing the confocal detection volume with two-photon excitation / N. Sandeau, H. Giovannini // Optics Communications. – 2006. – Vol. 264. – P. 123-129.

• 16.    Bokor, N. A three dimensional dark focal spot uniformly surrounded by light / N. Bokor, N. Davidson // Optics Communications. – 2007. – Vol. 279. – P. 229-234.

• 17.    Chen, Z. 4pi focusing of spatially modulated radially polarized vortex beams / Z. Chen, D. Zhao // Optics Letters. – 2012. – Vol. 37, Issue 8. – P. 1286-1288.

• 18.    Khonina, S.N. Shaping of spherical light intensity based on the interference of tightly focused beams with different polarizations / S.N. Khonina, A.V. Ustinov, S.G. Volotovsky // Optics & Laser Technology. – 2014. – Vol. 60. – P. 99-106.

• 19.    Хонина, С.Н. Исследование встречной интерференции остросфокусированных пучков с различной поляризацией / С.Н. Хонина, Н.С. Фидирко // Известия Самарского научного центра РАН. – 2014. – Т. 16, № 4. – С. 27-33.

• 20.    Chen, W. Three-dimensional focus shaping with cylindrical vector beams / W. Chen, Q. Zhan / Optics Communications. – 2006. – Vol. 265. – P. 411-417.

• 21.    Jabbour, T.G. Vector diffraction analysis of high numerical aperture focused beams modified by two- and three-zone annular multi-phase plates / T.G. Jabbour, S.M. Kuebler // Optics Express. – 2006. – Vol. 14, Issue 3. – P. 1033-1043.

• 22.    Gao, X. Focusing properties of concentric piecewise cylindrical vector beam / X. Gao, J. Wang, H. Gu, W. Xu // Op-tik. – 2007. – Vol. 118. – P. 257-265.

• 23.    Khonina, S.N. Controlling the contribution of the electric field components to the focus of a high-aperture lens using binary phase structures / S.N. Khonina, S.G. Volotovsky // Journal of the Optical Society of America A. - 2010. - Vol. 27(10). - P. 2188-2197.

• 24.    Khonina, S.N. Vortex phase transmission function as a factor to reduce the focal spot of high-aperture focusing system / S.N. Khonina, N.L. Kazanskiy, S.G. Volotovsky // Journal of Modern Optics. – 2011. – Vol. 58, Issue 9. – P. 748-760.

• 25.    Khonina, S.N. Influence of vortex transmission phase function on intensity distribution in the focal area of high-aperture focusing system / S.N. Khonina, N.L. Kazanskiy and S.G. Volotovsky // Optical Memory and Neural Networks (Information Optics). – 2011. – Vol. 20, Issue 1. – P. 23-42.

• 26.    Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications / Qiwen Zhan // Advances in Optics and Photonics. – 2009. – Vol. 1. – P. 1457.

• 27.    Хонина, С.Н. Формирование тонкой световой трубки при острой фокусировке азимутально-поляризованного излучения / С.Н. Хонина, А.В. Устинов // Известия Самарского научного центра РАН. – 2012. – Т. 14, № 6. – P. 279-284.

• 28.    Bouchal, Z. Non-diffractive vector Bessel beams / Z. Bouchal, M. Olivík // Journal of Modern Optics. – 1995. – Vol. 42, Issue 8. – P. 1555-1566.

• 29.    Dudley, A. Generating and measuring nondiffracting vector Bessel beams / A. Dudley, Y. Li, T. Mhlanga, M. Escuti, A. Forbes // Optics Letters. – 2013. – Vol. 38, Issue 17. – P. 3429-3432.

• 30.    Kotlyar, V.V. An algorithm for the generation of laser beams with longitudinal periodicity: rotating images / V.V. Kotlyar, V.A. Soifer, S.N. Khonina // Journal of Modern Optics. – 1997. – Vol. 44, Issue 7. – P. 1409-1416.

• 31.    Paakkonen, P. Rotating optical fields: experimental demonstration with diffractive optics / P. Paakkonen, J. Lauta-nen, M. Honkanen, M. Kuittinen, J. Turunen, S.N. Khonina, V.V. Kotlyar, V.A. Soifer, A.T. Friberg // Journal of Modern Optics. – 1998. – Vol. 45, Issue 11. – P. 2355-2369.

• 32.    Порфирьев, А.П. Простой способ формирования полых недифрагирующих световых пучков с распределением интенсивности в виде контура правильного многоугольника / А.П. Порфирьев, Р.В. Скиданов // Компьютерная оптика. – 2014. – Т. 38, № 2. – С. 243-248.

• 33.    Фидирко, Н.С. Формирование трёхмерных распределений интенсивности при дифракции лазерного излучения на кольцевых апертурах в условиях острой фокусировки / Н.С. Фидирко, С.Н. Хонина // Известия Самарского научного центра РАН. – 2014. – Т. 16, № 6. – C. 19-25.