АНАЛИЗ ИСПОЛЬЗОВАНИЯ ОТФИЛЬТРОВАННЫХ С ПОМОЩЬЮ ПОЛОСОВОГО ФИЛЬТРА ХАОТИЧЕСКИХ СИГНАЛОВ ДЛЯ ПЕРЕДАЧИ ДАННЫХ В СИСТЕМАХ РАДИОСВЯЗИ

Из литературы [1, 2] широко известно применение полосовых фильтров (ПФ) на приемной стороне различных систем радиосвязи для борьбы с помехами, которые воздействуют на передаваемые по каналу связи сигналы. Вместе с тем в последние годы стало развиваться и другое направление, связанное с использованием полосовых фильтров в системах радиосвязи, в частности [3, 4]. Они начинают находить применение для активно развивающегося в настоящее время направления: генерирования хаотических сигналов для систем радиосвязи. Исходя из этого, исследование и анализ хаотических сигналов, создаваемых при помощи полосовых фильтров для беспроводных систем передачи, представляет практический и научный интерес. Причиной такого интереса является [3–7] то, что полосовой фильтр при соответствующих настройках потенциально может заметно влиять на характеристики колебаний, и возникающие изменения должны быть учтены при диагностике получаемых сигналов.

Так, например, в работе [5] исследовалось прохождение сигналов, генерируемых аттрактором Ресслера, через полосовой фильтр. В результате проведенных исследований было установлено, что фильтрация хаотического сигнала в некоторых случаях приводит к изменению структуры аттрактора, усложняя ее, т.е. увеличивается хаотичность аттрактора. В работах [3, 4] данная идея была развита и апробирована для систем радиосвязи. В частности, в работе [4] с помощью полосовой фильтрации хаотических сигналов исследуется повышение скрытности передачи бинарного сообщения в системах радиосвязи. В предлагаемом подходе проводилось фильтрование широкополосным полосовым фильтром (ШПФ) отображения в виде полинома Чебышева, которое в дальнейшем использовалось в качестве генератора хаотических сигналов. Проведенные исследования показали [4], что отфильтрованный хаотический сигнал имеет аттрактор, схожий с аттрактором белого шума, в том время как аттрактор исходного хаотического сигнала структурирован. Показано применение полученных данных для повышения скрытности передачи бинарного сообщения в системах радиосвязи с корреляционным методом приема. Вместе с тем авторы работы [4] указывают на важное обстоятельство — для надежного функционирования систем радиосвязи данного класса необходимо, чтобы была правильно подобрана оптимальная полоса пропускания ШПФ при генерировании хаотических сигналов, которая бы одновременно обеспечивала наилучшие показатели скрытности и надежности функционирования (т.к. в данном случае надежность функционирования приемопередающей аппаратуры обратно пропорциональна скрытности). Это связано прежде всего с тем, что чем ýже полоса пропускания фильтра, тем в большей мере фазовый портрет генерируемого хаотического сигнала подобен фазовому портрету белого шума. Однако это отрицательно сказывается на надежности функционирования системы радиосвязи.

В связи со сказанным в данной работе авторы хотят более подробно рассмотреть вопросы использования отфильтрованных через ШПФ хаотических сигналов для обеспечения скрытности и надежности передачи данных в системах радиосвязи.

Задачей данной работы является получение временн . х реализаций хаотических сигналов, сгенерированных генераторами Чуа и Рикитаке, их фильтрация ШПФ и исследование полученных данных с помощью показателей BDS-статистики w ( ε ) и пик-фактора P .

ОСНОВНАЯ ЧАСТЬ

Краткие сведения о полосовых фильтрах и их применении к фильтрации хаотических сигналов

В соответствии с известными работами [4, 8], полосовой фильтр представляет собой линейную систему, состоящую из фильтра нижних частот и фильтра верхних частот. Полосовые фильтры бывают широкополосными и узкополосными. В соответствии с работой [8], к ШПФ относятся фильтры, у которых F C2 / F C1 > 1.5, а к узкополосным — F C2 / F C1 ≤ 1.5, где F C1 — нижняя граница частотного среза, F C2 — верхняя граница частотного среза.

Исследования будем проводить в соответствии с рекомендациями и выводами из работ [4, 5]. В соответствии с ними для преобразования хаотического сигнала к более сложному виду необходимо использовать ШПФ. Кроме того, в работах [4, 5] указывается, что при использовании ПФ с широкой полосой пропускания для фильтрации

хаотических сигналов их аттрактор изменяется незначительно. В случае же использования ПФ с узкой полосой пропускания для фильтрации хаотических сигналов, их аттрактор значительно усложняется.

Исходя из этого, проведем исследования в соответствии со следующим алгоритмом:

• 1)    получим временн . е реализации хаотических сигналов без фильтрации и проведем их исследование;

• 2)    получим временн . е реализации хаотических сигналов, отфильтруем их с помощью ПФ с широкой полосой пропускания и проведем их исследование;

• 3)    получим временн . е реализации хаотических сигналов, отфильтруем их с помощью ПФ с узкой полосой пропускания и проведем их исследование;

• 4)    проведем сравнение полученных результатов.

Исследовательская часть

В качестве первого генератора хаотических сигналов возьмем известный генератор Чуа, описываемый следующим выражением [9]:

х 1 = а[x 2 - x 1 - h ( x 1 )],

■ x2

= x ₃

-

x ₂

- ^x 1 ,

x 3 = ex 2 .

Временн . е реализации генератора Чуа без фильтрации; генератора Чуа, отфильтрованного с помощью ПФ с широкой полосой пропускания; генератора Чуа, отфильтрованного с помощью ПФ с узкой полосой пропускания, в соответствии с предложенным выше алгоритмом исследования авторами получены в пакете программ ScicosLab согласно рекомендациям из работ [4, 5, 9].

Примеры их фазовых портретов, построенных с помощью программы Fractan, приведены на рис. 1–3 соответственно.

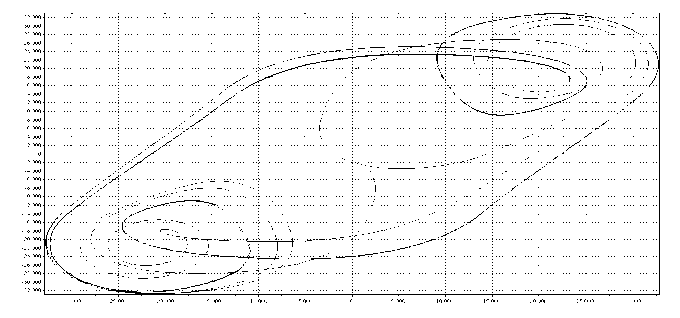
Рис. 1. Фазовый портрет временнóй реализации генератора Чуа (без фильтрации)

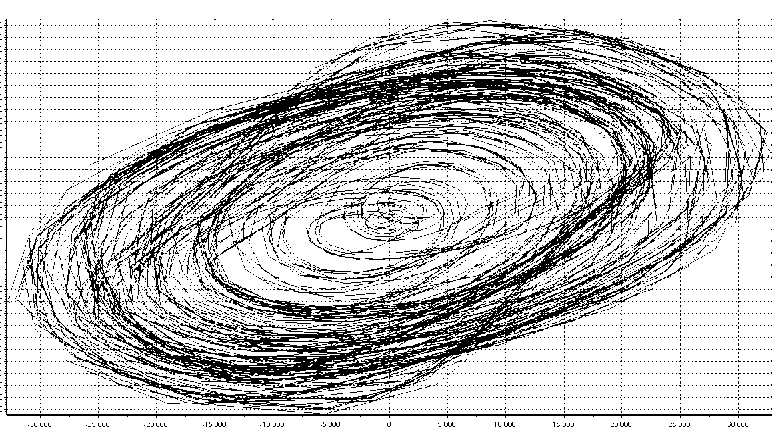
Рис. 2. Фазовый портрет временнóй реализации генератора Чуа, полученной с помощью ПФ с широкой полосой пропускания (ШПФ)

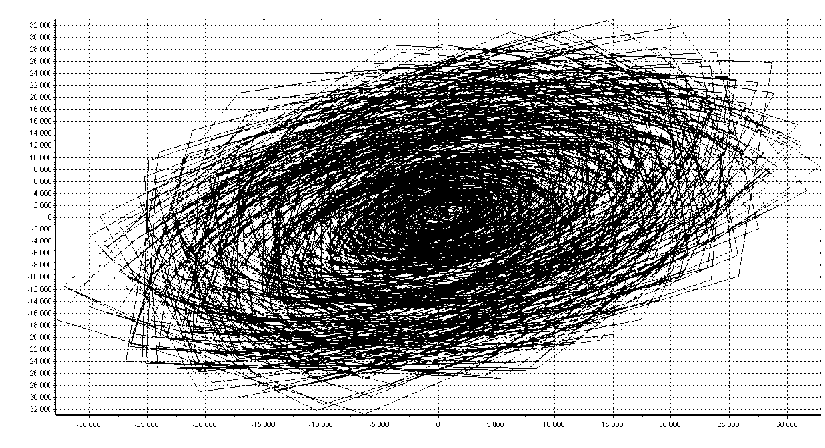
Рис. 3. Фазовый портрет временнóй реализации генератора Чуа, полученной с помощью ПФ с узкой полосой пропускания

Как видно из рис. 1, генератор Чуа (без фильтрации) обладает "классическим" фазовым портретом, который является структурированным. На рис. 2, 3 изображены усложненные фазовые портреты генератора Чуа, причем фазовый портрет, полученный с помощью ПФ с узкой полосой пропускания, является наиболее хаотичным. Полученные данные согласуются на качественном уровне с исследованиями из работ [4, 5].

В качестве второго генератора хаотических сигналов возьмем известный генератор Рикитаке, описываемый следующим выражением [10, 11]:

х = -цх + zy, y = -цх + (z - a)x,           (2)

Z = 1 - xy.

Временн . е реализации генератора Рикитаке (без фильтрации); генератора Рикитаке, отфильтрованного с помощью ШПФ; генератора Рикитаке, отфильтрованного с помощью ПФ с узкой полосой пропускания, в соответствии с предложенным выше алгоритмом исследования авторами получены в пакете программ ScicosLab, согласно рекомендациям из работ [4, 5, 10, 11]. На рис. 4–6 приведены примеры их фазовых портретов соответственно.

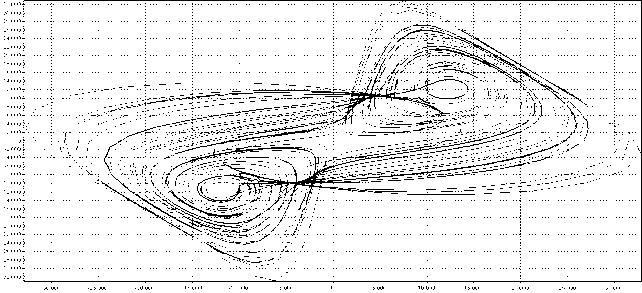
Рис. 4. Фазовый портрет временнóй реализации генератора Рикитаке

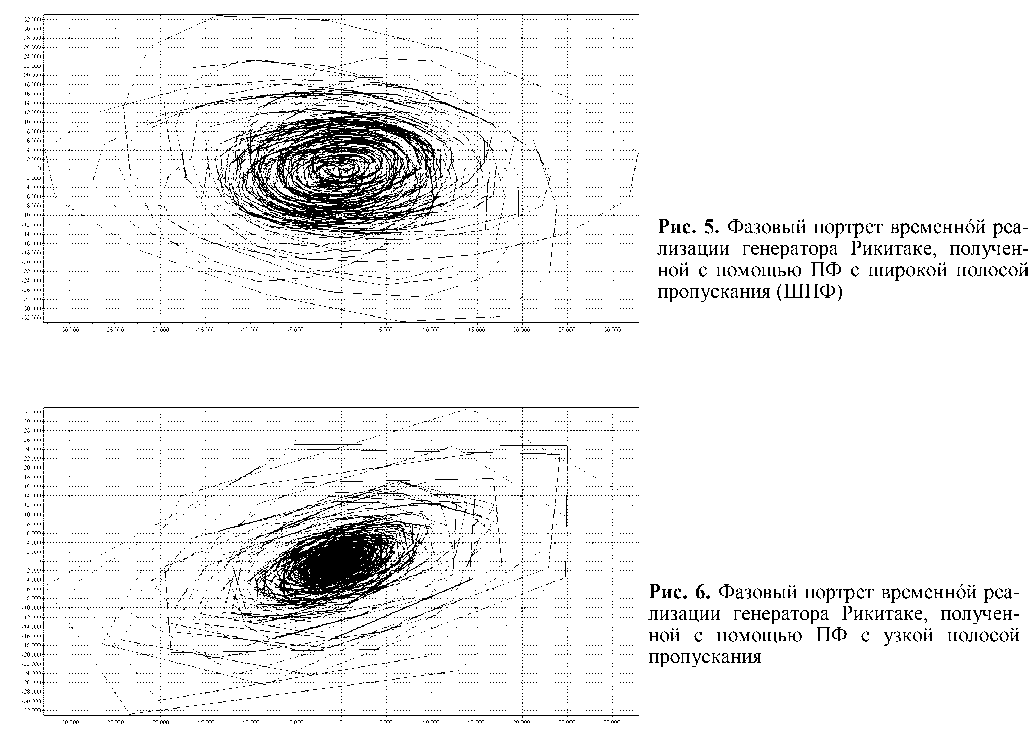
Как видно из рис. 4, генератор Рикитаке (без фильтрации) обладает "классическим" фазовым портретом, который является структурированным. На рис. 5, 6 изображены усложненные фазовые портреты генератора Рикитаке, причем фазовый портрет, полученный с помощью ПФ с узкой полосой пропускания, является наиболее хаотичным. Полученные данные также согласуются на качественном уровне с исследованиями из работ [4, 5].

Далее проведем количественную оценку скрытности полученных временн.х реализаций. Для осуществления количественной оценки скрытности обратимся к BDS-статистике, которая базируется на статистических свойствах корреляционной размерности исследуемого процесса в фазовом пространстве, которая в свою очередь определяется корреляционным интегралом. Эти данные дают в отдельных случаях больше информации о классе процесса (случайные, хаотические, регулярные), чем энергетические показатели. Таким образом, BDS-статистика в ряде случае может выступить в качестве меры энергетической скрытности [12–14]. BDS-статистика основана на стати- стической величине w(ε) [12–14], описываемой следующим выражением:

, А П5----ГТ Cm,N (£) - C1N-m ^)”     ПЛ wm N (£) = VN - m + 1 —2------------,    (3)

^,                             σ_{m , N} ( ε )

где C m , N (е ) и С 1, _{N -} m (е ) — корреляционные интегралы, а σ_{m , N} ( ε ) — среднеквадратичное отклонение.

В табл. 1 приведены значения BDS-статистики w ( ε ), описываемой выражением (3), для исследуемых временн . х реализаций. Расчеты авторами проведены с помощью программы Eviews Student Version Lite. Как видно из табл. 1, временн . е реализации генератора Чуа (без фильтрации) и генератора Рикитаке (без фильтрации) обладают значениями BDS-статистики w(е ) е [ 250 ^ 320 ] и w(е ) е [ 150 ^ 200 ] соответственно. Согласно известным исследованиям [12–15], это указывает на то, что временн . е реализации генератора Чуа и генератора Рикитаке обладают недостаточной

Табл. 1. Значения BDS-статистики w(s ), исследуемых временн . х реализаций генератора Чуа и генератора Рикитаке

Исследуемая система	BDS-статистика w ( ε )
Генератор Чуа
Генератор Чуа (без фильтрации) Фильтрация с помощью ШПФ Фильтрация с помощью ПФ с узкой полосой пропускания	[250÷320] [108÷130] [45÷50]
Генератор Рикитаке
Генератор Рикитаке (без фильтрации) Фильтрация с помощью ШПФ Фильтрация с помощью ПФ с узкой полосой пропускания	[150÷200] [74÷84] [43÷49]

скрытностью от постороннего наблюдателя, т.к. их значение BDS-статистики w(s ) >  200.

Временн . е реализации генератора Чуа и генератора Рикитаке, отфильтрованные с помощью ПФ с широкой полосой пропускания, об л адают значениями BDS-статистики w(s ) е [108 ^ 130] и w ( s ) е [74 ^ 84] соответственно. Согласно известным исследованиям [12–15], это указывает на то, что они обладают значением BDS-статистики w ( ε ) в несколько раз меньшим, чем установлено для хаотических сигналов ( w(s ) >  200). С учетом того, что изначально они были получены с помощью генератора Чуа и генератора Рикитаке, то их скрытность от постороннего наблюдателя является достаточной. Временн . е реализации генератора Чуа и генератора Рикитаке, отфильтрованные с помощью ПФ с узкой полосой пропускания, обладают значениями BDS-статистики w(s ) е [45 ^ 50] и w(s ) е [43 ^ 49] соответственно. Согласно известным исследованиям [12–15], это указывает на их схожесть с авторегрессионным и близкими к нему процессами. С учетом того, что они были получены с помощью генератора Чуа и генератора Рикитаке, то их скрытность от постороннего наблюдателя является достаточной. Полученные данные согласуются с исследованиями из работ [4, 5].

Проведем количественную оценку полученных временн.х реализаций с помощью одного из показателей надежности функционирования передачи данных в системах радиосвязи. В качестве такого показателя обратимся к известному показателю пик-фактора сигналов. Как известно из литературы [16, 17], увеличенное значение пик-фактора ограничивает реализуемые значения энергетической эффективности радиопередающего устройства, снижает помехоустойчивость приема, усложняет и удорожает применяемую аппаратуру. Значение пик-фактора сигнала вычисляется с помощью следующего выражения:

P =

U max

^, σ

где U max — максимальное значение сигнала, σ — среднеквадратичное значение сигнала.

В табл. 2 приведены значения пик-фактора P , описываемого выражением (4), для исследуемых временн . х реализаций. Расчеты авторами проведены с помощью программы ScicosLab.

Как видно из табл. 2, временн . е реализации генератора Чуа (без фильтрации) и генератора Рики-таке (без фильтрации) обладают наименьшим пик-фактором из рассмотренных сигналов, равным P <  3. Временн . е реализации генератора Чуа и генератора Рикитаке, отфильтрованные с помощью ШПФ, обладают значением пик-фактора P е [2.3 ^ 3.4] и P е [3.8 ^ 4.5] соответственно. Временн . е реализации генератора Чуа и генератора Рикитаке, отфильтрованные с помощью ПФ с узкой полосой пропускания, обладают значением пик-фактора P е [3.9 ^ 5] и P е [6 ^ 8] соответственно. Согласно известным исследованиям [16, 17], для современных систем связи значение пик-фактора передаваемых сигналов, вычисленное с помощью выражения (4), должно находиться примерно в диапазоне P е [1 ^ 4]. Отсюда можно заключить, что сигналы, полученные с помощью ПФ с узкой полосой пропускания, не подходят для систем радиосвязи, т.к. обладают повышенным значением пик-фактора. Вместе с тем остальные сигналы потенциально возможно использовать для систем радиосвязи. Полученные данные согласуются с исследованиями из работы

Табл. 2. Значения пик-фактора P исследуемых временн . х реализаций генератора Чуа и генератора Рикитаке

Исследуемая система	Пик-фактор P
Генератор Чуа
Генератор Чуа (без фильтрации) Фильтрация с помощью ШПФ Фильтрация с помощью ПФ с узкой полосой пропускания	≤3 [2.3÷3.4] [3.9÷5]
Генератор Рикитаке
Генератор Рикитаке (без фильтрации) Фильтрация с помощью ШПФ Фильтрация с помощью ПФ с узкой полосой пропускания	≤3 [3.8÷4.5] [6÷8]

Табл. 3. Обобщенные выводы по проведенным исследованиям

Исследуемая система	BDS-статистика	Пик-фактор
Генератор Чуа
Генератор Чуа (без фильтрации)	—	+
Фильтрация с помощью ШПФ	+	+
Фильтрация с помощью ПФ с узкой полосой пропускания	+	—
Генератор Рикитаке
Генератор Рикитаке(без фильтрации)	—	+
Фильтрация с помощью ШПФ	+	–/+
Фильтрация с помощью ПФ с узкой полосой пропускания	+	—

Сравнительный анализ полученных данных

В табл. 3 приведены обобщенные выводы по проведенным исследованиям.

Сравнительный анализ полученных данных (табл. 3) показывает, что для выбранных условий исследования в целом подходящими являются временн . е реализации генератора Чуа и генератора Рикитаке, полученные фильтрацией ПФ с широкой полосой пропускания (обладают п риемлемыми значениями BDS-статистики w ( ε ) и пик-фактора P ).

Таким образом, возможно сделать вывод, что фильтрация хаотических сигналов с помощью ШПФ при соблюдении определенных требований является перспективным подходом для обеспечения скрытности и надежности передачи данных в системах радиосвязи.

ЗАКЛЮЧЕНИЕ

В результате проведенных исследований получены временн.е реализации хаотических сигналов, сгенерированных на основе известных генератора Чуа и генератора Рикитаке. Проведена их фильтрация с помощью ШПФ и исследование полу- ченных данных с помощью показателей BDS-статистики w(ε) и пик-фактора P. В результате проведенных исследований установлено, что для выбранных условий исследования в целом приемлемыми являются временн.е реализации генератора Чуа и генератора Рикитаке, полученные фильтрацией ПФ с широкой полосой пропускания (обладают приемлемым значением BDS-статистики w(ε) и пик-фактора P). Другие рассмотренные временн.е реализации, в частности генератора Чуа и генератора Рикитаке без фильтрации, а также полученные их фильтрацией ПФ с узкой полосой в целом не подходят для систем радиосвязи, т.к. либо обладают недостаточной скрытностью от постороннего наблюдателя, либо обладают повышенным значением пик-фактора. Из этого можно заключить, что фильтрация хаотических сигналов с помощью ШПФ при соблюдении определенных требований является перспективным подходом для обеспечения скрытности и надежности передачи данных в системах радиосвязи. Вместе с тем она так же имеет и ограничения, которые необходимо учитывать при ее использовании. В частности, следует обращать внимание на влияние полученных при фильтрации сигналов на скрытность и надежность передачи данных в системах радиосвязи. Данный вывод согласуется с выводами из работы [4].

Авторы на основе проведенных исследований и выводов из известных работ [4, 5] считают целесообразным применять для обеспечения скрытности и надежности передачи данных в системах радиосвязи при использовании хаотических сигналов наряду с широко распространенными методами (например, расширением базы передаваемых сигналов, помехоустойчивым кодированием и др.) также и фильтрацию хаотических сигналов с помощью ПФ с широкой полосой пропускания. Вместе с тем данное утверждение требует дальнейших исследований с учетом апробации на значительно большем количестве генераторов хаотических сигналов. Кроме того, в перспективе необходимо обратить внимание на вопросы синхронизации в таких системах, а также на вопросы усложнения приемопередающей аппаратуры, которые неизбежно возникают в таких случаях.