Анализ эффективности использования резонансных режимов в импульсных высокочастотных преобразователях напряжения

Одним из перспективных направлений развития импульсных преобразователей электроэнергии является использование резонансных режимов работы регулирующего элемента – электронного ключа, коммутация которого происходит с минимальными потерями мощности [1–3]. Актуальность развития и совершенствования преобразовательной электроники во многом продиктована возрастанием популярности распределенных систем электропитания, которая влечет за собой увеличение спроса на различные типы DC/DC- и AC/DC-преобразователей. Распределенные системы стали стратегической архитектурой, если не всеобщим решением проблемы электропитания цифровых и телекоммуникационных систем. По мере распространения распределенных систем на контрольно-измерительную аппаратуру, технологическое оборудование, системы автоматики и телемеханики, охранные системы и т. д. преимущества распределенного электропитания становятся все более очевидными. Одновременно происходит расширение номенклатуры модулей, применяемых в распределенных системах электропитания, и повышение требований к качеству преобразователей [4].

По сравнению с классическими преобразователями напряжения (ПН), использующими широтно-импульсный закон регулирования, резонансные (квазирезонансные) ПН являются более сложным объектом управления, что обусловлено нелинейной зависимостью передаточной характеристики силовой части по постоянному току от тока нагрузки и напряжения питания [3; 5; 6]. Поэтому для обеспечения надежной работы ПН с резонансным контуром (РК) необходимо определить ограничения, налагаем на режимы управления резонансными ключевыми элементами. С другой стороны, из-за перераспределения энергии в РК возрастают амплитудные значения тока и напряжения на электронных ключах, повышающие статические потери мощности.

В данной статье исследованы два варианта квазирезо-нансного ПН с коммутацией при нулевых значениях тока, которые могут найти применение в распределенных системах электропитания.

Эффективность преобразователей постоянного напряжения может определяться следующими показателями: удельной мощностью, КПД и уровнем электромагнитных помех (ЭМП). Первые два параметра непосредственно связаны между собой, так как повышение удельной мощности возможно только за счет увеличения частоты преобразования при обеспечении заданного уровня пульсаций выходного напряжения и тока, что в классических схемах ПН приводит к увеличению потерь мощ- ности на переключение ключевого элемента (КЭ) и в магнитных цепях. Это в свою очередь связано с необходимостью введения дополнительных мер по съему тепловой энергии с силовых полупроводниковых компонентов ПН.

Снижение коммутационных и статических потерь мощности в классических импульсных преобразователях напряжения с широтно-импульсной модуляцией (ШИМ) может быть достигнуто за счет совершенствования элементной базы: повышения быстродействия ключевых элементов и уменьшения падения напряжения на КЭ в открытом состоянии. Но это только усилит влияние паразитных реактивных элементов реальной схемы, так как увеличение скорости изменения напряжения и тока на коллекторе (стоке) КЭ приводит к возрастанию амплитуды высших гармоник сигнала, частоты которых могут совпадать с собственными частотами резонансных контуров, образованных паразитными элементами схемы, что в свою очередь увеличивает высокочастотные помехи, наложенные на выходное напряжение ПН. Так, например, из-за конструктивных особенностей дросселей и конденсаторов в их составе неизбежно присутствуют паразитные реактивные элементы, исключить которые в реальной схеме полностью невозможно [7; 8]. Бороться с этим можно за счет введения в силовую часть схемы различных демпфирующих цепей, что влечет за собой дополнительные потери энергии. С другой стороны, из-за высокой скорости нарастания сигнала на стоке (коллекторе) силового транзистора может происходить наведение помех на другие элементы схемы или электронные устройства.

Таким образом, наиболее эффективным путем одновременного повышения указанных выше показателей эффективности высокочастотных преобразователей постоянного напряжения может быть применение резонансных режимов электронного ключевого элемента. По мнению автора, это единственный рациональный путь снижения электромагнитных помех в высокочастотной области.

Однако повышение частоты преобразования влечет за собой принятие мер по борьбе с эффектом вытеснения тока, т. е. применение планарных трансформаторов и индуктивных элементов, обмотки которых могут быть реализованы печатным способом, что в то же время приводит к увеличению паразитной межвитковой емкости. Следовательно, и с этой точки зрения повышение частоты преобразования оправдывает применение резонансных режимов в импульсных преобразователях несмотря на некоторые их ограничения.

Обобщая сказанное выше, мы можем сформулировать следующее утверждение: одновременное повыше- ние удельной мощности и КПД для резонансного (ква-зирезонансного) ПН по сравнению с классическим ПН при

равных условиях, возможно при выполнении неравенства

р + р +р д.ШИМ + ст.ШИМ + тр

Р + Р + Р +Р„„ д.рез      ст.рез      тр      РК

> 1,

где P _д.ШИМ – динамические потери при жестком переключении КЭ в режиме ШИМ; P _д.рез – динамические потери КЭ в резонансном режиме (как правило, несуществен-

ные); P _ст.рез, P _ст.ШИМ – статические потери пассивных и активных ключей в резонансном и ШИМ-режимах соответственно; P _тр, P _РК – потери мощности в трансформаторе (в случае его применения) и элементах РК. Прибли-

женное значение мощности коммутационных потерь в транзисторных МДП-ключах при условии, что ПН рабо-

тает в режиме непрерывного тока дросселя выходного

фильтра [9], можно найти по формуле

^ д. ШИМ = 2 I с U СИ ( t on + t off ) f к + 2 C си U си ² f _: ,    (²)

где U _СИ – напряжение стока-истока в закрытом состоянии МДП-ключа; I _c – коммутируемый ток (ток стока); С _СИ – емкость стока-истока МДП-транзистора; t _on, t _off – время отпирания и запирания МДП-транзистора соот-

ветственно; f _к – частота коммутации.

Оценку статических потерь в полупроводниковых

транзисторных ключах проведем путем их сравнения с аналогичными потерями в режиме ШИМ с жестким переключением КЭ при равных входном и выходном напряжении и токе нагрузки. Такая относительная оценка позволит более наглядно оценить разницу между режимами при выборе типа преобразователя для проектируе-

мого источника вторичного электропитания.

Импульсные преобразователи могут производить два типа электромагнитных помех [7]: ЭМП, генерируемые непосредственно импульсной работой КЭ, и ЭМП, генерируемые паразитными РК электрической схемы в моменты отпирания или запирания КЭ.

Электромагнитные помехи, генерируемые непосредственно импульсной работой КЭ, могут быть проанализированы путем разложения функций сигналов тока и напряжения в ряд Фурье [7]:

+

f N ( t ) =+

£ ( a n ■ cos ( n ■ t ) + b n ■ Sin

n = 1

(n ■ t))

12π                     12π a о =- Jf (t )dt, an = -J f (t) cos (n ■ t) dt, π0                π0

12π bn =      f (t) sin (n ■ t) dt,

π0

A n = V a n ² + b n ²,

• (4)

• (5)

гичными амплитудами в режиме ШИМ с жестким переключением КЭ при прочих равных условиях.

Электромагнитные помехи, генерируемые за счет паразитных элементов, как правило, имеют узкий спектр с максимальной амплитудой гармоники, соответствующей собственной частоте паразитного РК. В случае если один из элементов паразитного РК носит нелинейный характер, как, например, барьерная емкость диода или емкость стока-истока МДП-транзистора, то генерируемая помеха может иметь более широкий спектр. Такой тип помех зависит главным образом от используемой элементной базы, условий монтажа и компоновки элементов преобразователя на печатной плате. Поэтому теоретический анализ помех такого рода затруднителен и сводится, как правило, к экспериментальным исследованиям.

Данная статья посвящена анализу резонансного режима с коммутацией ключевого элемента при нулевых значениях тока. Основная идея использования данного режима состоит в том, что ток ключевого элемента, включенного последовательно с индуктивностью РК, изменяется по гармоническому закону, отпирание и запирание электронного ключа происходит в моменты прохождения тока через нулевые значения (или близкие к ним), причем из-за малой скорости нарастания тока по сравнению со скоростью переключения транзистора динамические потери мощности сведены к минимуму. Указанный режим предполагает два возможных варианта:

– с половиной волны резонансного цикла (ПНТ¹) (рис. 1, 2, а ) [2; 5; 6]. В этом варианте после открытия ключа начинается процесс, при котором ток ключа и резонансной индуктивности сначала линейно возрастает до значения, равного току нагрузки, после чего диод VD3 закрывается. Дальнейшее изменение тока ключа происходит по гармоническому закону. Когда ток ключа достигает нулевого уровня, происходит запирание диода VD2. В этот момент должно происходить выключение ключевого элемента, что обеспечит минимум динамических потерь. Характерным недостатком данной схемы является наличие проходного диода VD2, который увеличивает внутренние потери преобразователя. Для преодоления этого недостатка может быть использовано решение, предложенное в [10];

– с полной волной резонансного цикла (ПНТ²) (рис. 2, б ). Отличие этого варианта от предыдущего состоит в том, что ток L _р, достигая нулевого значения, меняет знак, при этом часть энергии, запасенной в С _р, не рекуперируется в нагрузку, а возвращается в первичный источник. Такой режим может быть реализован, если исключить диод VD2 в схеме на рис. 1 [3]. По сравнению с предыдущим этот вариант имеет более линейную регулировочную характеристику.

где f_N ( t ) – уравнение ряда Фурье; a ₀, a_n , b_n – коэффициенты Фурье; A_n определяет амплитуду n -й гармоники; f ( t ) – функция времени исследуемого сигнала. Фурье-анализ сигналов в цепи КЭ также позволит оценить амплитуды высших гармоник, на которых паразитные РК реальной схемы могут входить в резонанс. Анализ ЭМП, как и оценку статических потерь преобразователей исследуемого типа, будем проводить путем сравнения амплитуд гармонических составляющих сигналов в цепи КЭ с анало-

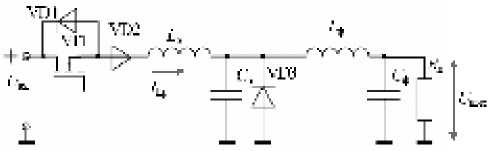
Рис. 1. Схема силовой части последовательного ПНТ1-преобразователя

Один период работы КЭ в цепи РК ПНТ¹-преобразо-вателя можно разбить на четыре временных интервала (см. рис. 2, а ), которые описываются выражениями

[ 0 <  t <  t i ] : <

I l p ( t ) = Ц х², L _р

U c р ( t ) = 0,

A t = t = ^{I h}- ^{L p}- ,

¹¹   U вх

[ t i <  t <  t 2 ] : <

sin (®o( t -t,))

I l p ( t ) = I н + U вх   —    -,

Z ₀

U CP р ( t ) = U вх ( ^{i -} cos ( ® 0 ( t ^- t i ) ) ) , .,    . . n , 1          . Z Z_o ■ /„

A t₂ = t ₂ - t = —+-- arcsin ——н

® 0   ® 0        I U вх

[ t 2 <  t <  t з ] : <

UCP (t ) = -

( t - t 2 ) Iн

C р

+

⁺ U вх ( 1 ^- cos ( ® 0 ⁽ t 2 ^-

I L P ( t ) = ^0;

A t 3 = t 3 - t 2 =

C

= "Г ^U вх ( 1 ^- cos ( ® 0 ( t 2 ^-

I _н

I l p ( t ) = 0, U c р ( t ) = 0,

где I_{L р}( t ) – ток через индуктивность РК L _р; U_{C р}( t ) – напряжение на конденсаторе РК; I _н – ток нагрузки; Z ₀= ( L _р / С _р)^0,5 – волновое сопротивление РК; U _вх – напряжение питания преобразователя; ® ₀= 2 n / 0 = 1/( L _р С _p)⁰ - ⁵- собственная частота РК.

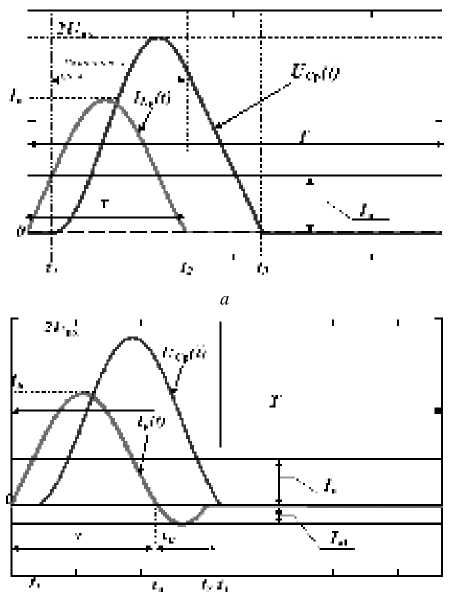
б

Рис. 2. Идеализированные временные диаграммы режимов: а – ПНТ¹; б – ПНТ²

Режим ПНТ² также можно разбить на четыре интервала (см. рис. 2, б ). От предыдущего случая его отличают только интервалы ( t ₁; t ₂) и ( t ₂; t ₃), которые описываются выражениями [3; 11]:

че

[ t i

*

sin ( ю₀ ( t - 1 ,))

Il p( t ) = I „ + U ------¹ ,

L рнвх

Z ₀

^U C р ( t ) = ^U вх ( 1 ^- cos ( ® 0 ( t ^- t i ) ) ) , (10) • ( LZ_n )

2n-arcsin I —⁰ I

A 1 2 = 1 2 - t i

U вх ^ω 0           ^,

U_{c p}( t ) = U =x i C р          вх

^- "Сн- ⁽ t ^- t 2 ) , I L P ( t ) = ^0;

A 1 3 = 1 3 - 1 2 =

U вх

i -

i -

-

i -

I н Z 0

U вх

-

I н Z 0

U вх

[           I н Z 0 ® 0

Для сравнительной оценки статических потерь на клю-введем относительный коэффициент потерь M _отн =

.

= P _КЭ.ШИМ/ P _КЭ.ПНТ, где P _КЭ.ШИМ – статическая мощность, рассеиваемая на ключе в открытом состоянии в режиме ШИМ; P _КЭ.ПНТ – мощность, рассеиваемая на ключе в открытом состоянии в режиме ПНТ.

В качестве КЭ может быть использован биполярный или МДП-транзистор. В первом случае относительный коэффициент потерь будет

^M отн

^U КЭ.отк ^I эф.ШИМ    ^I эф.ШИМ

^U КЭ.отк ^I эф.ПНТ

^, эф.ПНТ

где U _КЭ.отк – напряжение коллектора–эмиттера биполярного транзисторного ключа в открытом состоянии; I _эф.ПНТ – эффективный ток для любого из вариантов режима ПНТ. В случае использования МДП-транзистора

^M отн

^R отк ^I эф.ШИМ

^R отк ^I эф.ПНТ

I эф.ШИМ I

I , I эф.ПНТ J

где R _отк – сопротивление стока-истока транзисторного МДП-ключа в открытом состоянии.

Таким образом, далее необходимо определить эффективное (среднеквадратичное) значение тока, протекающего через КЭ. В общем случае эффективное значение тока любой формы [12] будет

I эф

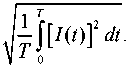
Для режима ШИМ, считая, что форма тока имеет строго прямоугольную форму, эффективный ток определим как

I эф.ШИМ    I a

где т - длительность импульса КЭ; T - период коммутации; I _a – амплитудное значение тока через ключ.

Для последовательного понижающего ПН справедливы следующие соотношения:

показывающий отношение эффективного значения тока КЭ в режиме ШИМ к эффективному току исследуемого

I a * I н ,

U вых

*

TU вх

.

Для дальнейших расчетов формулы (16) и (17) принимаем за строгие равенства.

Основные соотношения, определяющие эффективное значение тока КЭ для режимов ПНТ¹ и ПНТ², при условии, что ток имеет строго синусоидальную форму, представлены в табл. 1, в которой использованы следующие обозначения: U_Cр – усредненное по времени значение напряжения на конденсаторе РК, равное выходному напряжению в установившемся режиме при условии идеальности выходного фильтра; K_U – коэффициент передачи по напряжению; f _к – частота коммутации; K ₁( I _н) и K ₂( I _н) – коэффициенты, зависящие от тока нагрузки I _н для режима ПНТ¹ и ПНТ² соответственно:

K 1 (¹ - ⁾ = 2п ^{n +}

J ( I )

---—+ arcsin x

/           2

J ( I н )

K ( I - ⁾ = 27 2" ⁺

J ( I )

—^-— arcsin x

2     _

резонансного режима при прочих равных условиях, при-

чем найдем его как функцию от тока нагрузки:

I      (i )   Iэф.ШИМ (I- )   эф.отн1н

^I эф.ПНТ1 ^{( I} н ⁾

I -        1 ² K , ( I - ) / f 0

f I + Uвх P    T(I- )

l ^-

.      I j x _ ¹ эф.ШИМ ^{( 1} - ) _

• 1    эф.от-2 (J -)     у/ у

• Iэф.ПНТ2 (Iн )

• I -       1 2 K 2 ( I - ) / f 0

.

f I ₊ U вх P    T⁽ I - )

l ^-    Z 0 ^J

А поскольку режимы ПНТ1 и ПНТ2 имеют граничное условие по максимальному току нагрузки при прочих фик-

сированных параметрах, то можно рассчитать теоретический предел функций (19) и (20). Таким граничным условием является условие I _н Z ₀/ U _вх = 1 [13]. Подставляя его в функции (19) и (20), получим

^I эф.ШИМ

^I эф.ПНТ1

эф. ШИМ шим

^I эф.ПНТ2

* 0,737.

Представим некоторые кривые, показывающие отно-

шение между эффективными значениями тока через КЭ

J ( I н )

Так как M _отн определяется отношением эффективных токов, то целесообразно ввести относительный параметр,

для режимов ПНТ и ШИМ в зависимости от тока нагрузки с параметрами, указанными в табл. 2 (рис. 3, 4).

Наиболее приемлемыми топологиями для режима ПНТ, обеспечивающими гальваническую развязку, являются типы ПН, представленные на рис. 5. При этом все

Таблица 1

Параметр Режим ПНТ1 ПНТ2 Iэф IaA E a 2T a  2T Ia U I-+ Z0 U I- + ^х Z0 Ia1 – Uвх I- "^ Z0 τ f IZ) n + arcsin - 0 U Le^^ + р Uвх          ω0 f IZ 1 n + arcsin - 0 U L   +-------^_в^2 р Uвх          ω0 τn – f        f IZ11 n-2arcsin - 0 I          I U™ J J вх ω0 T T _ UBX K, (I-) u вых 0 T _ UвхK2(I-) *  Uвх Uвых f0     Uвых f0 J(Iн) IнZ0 Uвх IнZ0 Uвх KU U C-f- _ ( fк / fo) K1( I- ) Uвх U _ (f к / f 0) K2( I- ) * f к / f 0 Uвх аналитические соотношения будут такими же, как и в последовательной схеме в соответствии с режимом ПНТ1 или ПНТ2, с учетом того, что амплитудные значения тока и напряжения первичной и вторичной обмоток импульсного трансформатора связаны коэффициентом трансформации.

Как было сказано выше, теоретический анализ электромагнитных помех, создаваемых импульсной работой КЭ, можно проводить при помощи разложения в ряд Фурье функций времени сигналов в силовой цепи исследуемого ПН. Для этого определим амплитуду для n -й гармоники анализируемого сигнала в соответствии с (3)…(5), используя аналитические выражения (6)…(11), и введем относительную логарифмическую оценку амплитуд соответствующих гармоник тока ключа режимов ШИМ и ПНТ:

ШИМ

In °™ = 20log    ,, .                (22)

In

Покажем формы сигналов тока для разных режимов и их спектры (рис. 6) при прочих равных условиях, учитывая, что оба режима ПНТ имеют частотно-импульсный закон регулирования, а частота коммутации для режима ШИМ равна частоте для режимов ПНТ¹ и ПНТ² при I _н = 4,6 А, U _вх = 60 В и параметрах, заданных в табл. 2. Суммарная длительность фронтов t_r и t_f импульса тока в режиме ШИМ составляет порядка 3 % от длительности периода.

Таким образом, в результате проведенного анализа можно сделать следующие выводы:

– статические потери мощности на КЭ в режиме ПНТ по сравнению с режимом ШИМ при максимальной нагрузке и прочих равных условиях (входном и выходном напряжении, токе нагрузки) могут быть в 2…4 раза выше в зависимости от разницы между входным и выходным напряжением, причем для режима ПНТ2 относительные потери в КЭ выше, чем для режима ПНТ1, при условии

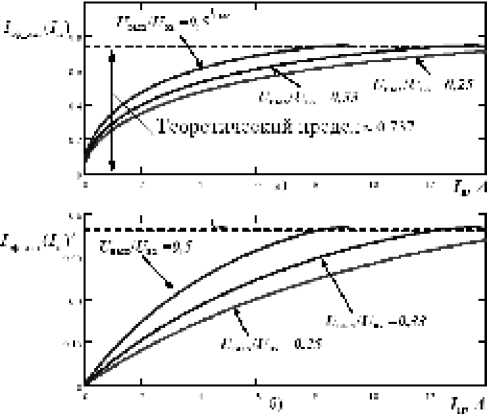
Рис. 3. График I эфо _тн1 ( I п ) для режима ПНТ¹

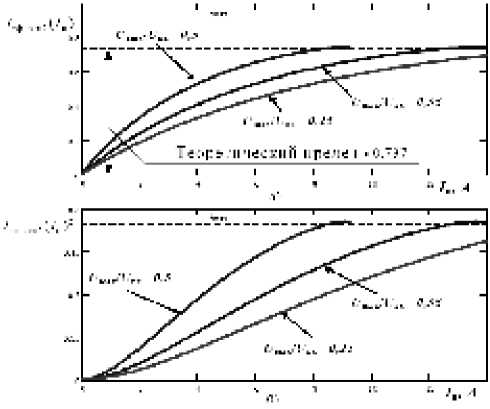
Рис. 4. График I эф _отн2 ( 1 п ) для режима ПНТ²

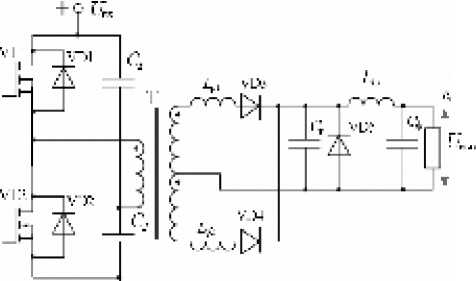
Рис. 5. Электрические схемы силовых частей полумостового ПН с режимом ПНТ¹ ( а ) и дифференциального ПН с режимом ПНТ² ( б )

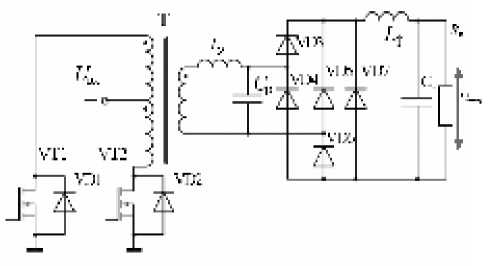
б

Таблица 2

Элемент Значение Lр, Гн 1,05 10–6 Cр, Ф 57 ∙ 10–9 Uвых, В 20 того, что в первом случае не учитываются потери за счет отрицательной полуволны тока индуктивности РК (см. рис. 2, б). Таким образом, режим ПНТ2 предполагает существенно большие статические потери на КЭ по сравнению с режимом ПНТ1;

– получены теоретические пределы отношений между статическими потерями в активных ключах квазирезо-нансного режима с коммутацией при нулевом токе и аналогичного режима с ШИМ при прочих равных условиях. Хотя функции (19), (20) имеют экстремум, а предельное значение (21) несколько ниже максимума, последнее может быть принято за теоретический предел определенного выше соотношения для обоих режимов с учетом того, что максимальное значение тока нагрузки (вертикальная пунктирная линия на рис. 3, 4) для режимов ПНТ1 и ПНТ2 существенно ниже значения, приходящегося на максимум функций (19) и (20) (см. рис. 3, 4);

– режимы ПНТ¹ и ПНТ² дают существенно меньший вклад высших гармоник в частотный спектр сигналов тока в цепи ключевого элемента по сравнению с режимом ПН с ШИМ. Амплитуда первой гармоники для тока в обоих случаях превышает аналогичные значения для режима ШИМ не более чем на 20 % при типовых параметрах РК, которые выбираются исходя из условия Z ₀ ≤ R _нmin, где R _нmin – минимальное сопротивление нагрузки.

Материалы данной статьи были подготовлены по результатам, полученным автором во время прохождения научной стажировки в Кассельском университете (Германия) на кафедре систем электроснабжения под руководством профессора П. Захариаса при финансовой поддержке грантов Министерства образования и науки Российской Федерации и Немецкой службы академических обменов (DAAD).