Анализ эффективности одношаговых численных методов решения задачи Коши для обыкновенного дифференциального уравнения первого порядка

Многие задачи различных отраслей науки и техники при их решении сводятся к дифференциальным уравнениям, в связи с чем решение последних является важной математической задачей. Особенно важна точность решения поставленных задач, а также время и затраченные на это усилия. Именно поэтому в данном вопросе в современном мире развивающихся технологий обязательно нужно использовать все его ресурсы, в частности вычислительную технику, для создания программного обеспечения, которое позволит использовать существующие численные методы для более точного и доступного решения важнейших задач, а также проверить эффективность данных методов.

Существует    множество    различных    методов    решения дифференциальных уравнений (ДУ) и, в том числе, задачи Коши. Будем рассматривать численные методы, так как они в настоящее время являются основным инструментом при исследовании научно-технических задач, описываемых дифференциальными уравнениями. Также стоит отметить, что данные методы особенно эффективны в сочетании с использованием современных компьютеров.

Задача Коши – одна из основных задач теории дифференциальных уравнений, состоящая в нахождении решения ДУ, удовлетворяющего заданным начальным условиям, или начальным данным. Дифференциальные уравнения делятся на два вида уравнений: обыкновенные ДУ с одной независимой переменной и уравнения с частными производными, содержащие несколько независимых переменных. Будем рассматривать задачу Коши для системы обыкновенных дифференциальных уравнений. Такие уравнения содержат одну или несколько производных от искомой функции.

Пусть имеем искомую функцию у = у(х). Тогда вид обыкновенных дифференциальных уравнений будет следующим: F(x,y,y', .„,у(п)) = 0, где х - независимая переменная, а n - наивысший порядок входящей в уравнение производной, который называется порядком дифференциального уравнения. Для простоты рассмотрим ОДУ первого порядка. Зачастую ОДУ можно свести к следующему виду: у' = f(x,y), или у" = f(x,y,y') (в зависимости от порядка уравнения), или, что то же самое, ^ = f(x,y).

Такая форма записи называется уравнением, разрешенным относительно старшей производной, и является наиболее понимаемой.

Производная у' по определению характеризует наклон касательной к графику решения у = у(х), то есть к интегральной кривой в данной точке, а также является константой: у' = к = const = f (х, у). Получаем f(x,y') = к - это уравнение линии постоянного наклона, которая называется изоклиной. При изменении к образуется семейство изоклин.

Прежде чем приступить к решению дифференциального уравнения, нужно разобраться, что значит решить ДУ. Решить ДУ значит найти такую функцию у = д)(х), которая после подстановки её в исходное уравнение превращает его в тождество. Решение может быть общим и частным. Общее решение - содержит такое определенное количество п произвольных постоянных С [ , каков порядок уравнения, в нашем случае такая постоянная будет одна, и представляется в следующем виде: у = ф(х,С 1 ,С 2 ,... ,С_п). Частное решение получается из общего, если произвольным постоянным придать определенные значения. Так, например, если для ДУ первого порядка общее решение будет выглядеть так: у = ^(х, С), то частное решение, при условии, что С = С₀, где С₀ - некоторое число, - так: у = ^(х, С₀). Решение задачи Коши - это частное решение, где С₀ находится с помощью подстановки в общее решение заданных начальных условий.

Итак, какие существуют численные одношаговые методы решения задачи Коши для ОДУ?

• • Метод Эйлера

Является простейшим численным методом решения задачи Коши, имеет первый порядок точности. Применяется сравнительно редко при небольшом количестве узлов. Пусть имеем уравнение, разрешенное относительно старшей производной, и начальные условия х₀ и у₀. Рассмотрим его в окрестностях узлов х , (i = 0,1,...). Будем считать, что х , равноотстоят друг от друга на шаг h, т.е. h_t = х ^ ₊₁ — х ^ = h = const. Тогда у ^ находится по следующей формуле:

У,+1 = У[ + hf(xi,yi)

Данным методом можно воспользоваться также и в случае, если необходимо найти решение задачи Коши на определенном отрезке [а,Ь]. Тогда %₀ следует взять равным а, а шаг h = ^^, где п - количество расчетных точек (узлов).

• • Модификации метода Эйлера

Существует две модификации метода Эйлера – это метод Эйлера с пересчетом, также известный как метод Эйлера-Коши, и усовершенствованный    метод    Эйлера,    также    называемый модифицированным методом Эйлера. Так как первый является более распространенным и оба они имеют второй порядок точности, рассмотрим лишь его.

h

• У [+1 = у< + 2 [f (ХьУ t) + f (xt+i>yt + hf (xi,yj))]

• • Методы Рунге-Кутта

Широко распространен метод Рунге-Кутта четвертого порядка, соответственно, имеющий четвертый порядок точности. Алгоритм этого метода записывается в следующем виде:

^yj+1 = ^yj ⁺ 7 ^(k1 ^{+ 2k}2 ⁺ 2^ 3 + ^ 4 ) , г^де О

^1 =f(xi,yi)

^2=f(xi+h,yi+h^1) k3=f(Xi+h,yi + h^2) ^4 = f(Xj + h,yt + hk3)

Для исследования эффективности и точности описанных выше методов была разработана программа на объектно-ориентированном языке программирования Java. Далее представлены результаты выполнения программы и диаграммы с сравнением графиков, полученных при работе методов Эйлера, Эйлера-Коши и Рунге-Кутта четвертого порядка, и эталонного решения, полученного аналитическим способом.

Пример 1:

У’sinx = ylny, %o = |,yo = y(Xo) = e

Эталонное решение 1 (далее – эталон):

x

У = etan2

Таблица 1.

x	1,6708	1,7708	1,8708		2,2708	2,3708	2,4708	2,5000
Эйлер	2,9901	3,3193	3,7256		7,0238	8,8139	11,5671	12,8975
Эйлер-Коши	3,0183	3,3920	3,8693		8,4130	11,3878	16,6784	19,1302
Рунге-Кутта	3,0203	3,3975	3,8810		8,5822	11,7616	17,6120	20,2722
Эталон	3,0203	3,3975	3,8810	…	8,5827	11,7630	17,6173	20,2787

Пример 2:

, y 2 -2xy-x²

^У = y²+2xy-x² ,    ^x 0 =  ^,У0 =

Эталон 2:

У = -X

Таблица 2.

x	1,10	1,20	1,30		1,70	1,80	1,90	2,00
Эйлер	-1,10	-1,20	-1,30		-1,70	-1,80	-1,90	-2,00
Эйлер-Коши	-1,10	-1,20	-1,30		-1,70	-1,80	-1,90	-2,00
Рунге-Кутта	-1,10	-1,20	-1,30		-1,70	-1,80	-1,90	-2,00
Эталон	-1,10	-1,20	-1,30	…	-1,70	-1,80	-1,90	-2,00

Пример 3:

y‘= 3x2y + X5 + X2,  Хо = О,Уо = 1

Эталон 3

5 з 1

У = ^ех --(2 + х3)

Таблица 3.

x	0,1000	0,2000	0,3000		0,7000	0,8000	0,9000	1,0000
Эйлер	1,0000	1,0030	1,0150		1,3051	1,5052	1,8152	2,3041
Эйлер-Коши	1,0010	1,0080	1,0273		1,4138	1,6856	2,1229	2,8484
Рунге-Кутта	1,0010	1,0080	1,0274		1,4171	1,6929	2,1394	2,8862
Эталон	1,0010	1,0080	1,0274	…	1,4171	1,6929	2,1394	2,8862

Из приведенной выше теоретической информации становится понятно, что общее решение на графике будет отражать все возможные подходящие решения, то есть семейство интегральных кривых, а частное решение – только одно из них, конкретное, то есть одну такую кривую. Для сравнения точности исследуемых методов построим такие кривые для каждого из них. Это позволит более наглядно увидеть точность работы каждого из используемых методов.

График для первого примера:

Эйлер      Эйлер-Коши      Рунге-Кутта      Эталон

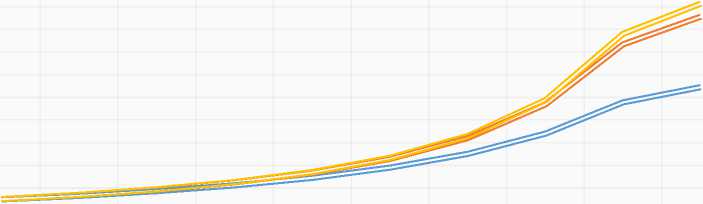
1,6708 1,7708 1,8708 1,9708 2,0708 2,1708 2,2708 2,3708 2,4708 2,5000

22,0000

20,0000

18,0000

16,0000

14,0000

12,0000

10,0000

8,0000

6,0000

4,0000

2,0000

0,0000

По графику можно сказать, что метод Рунге-Кутта наиболее точно, практически абсолютно повторяет эталонное решение, а метод Эйлера отрабатывает с достаточно большой погрешностью, что показывает его неэффективность для данного примера.

График для второго примера:

Эйлер      Эйлер-Коши      Рунге-Кутта      Эталон

0,0000

1,1000       1,2000       1,3000       1,4000       1,5000       1,6000

-2,0000

Ввиду того, что эталон представляет собой линейную функцию, все методы позволили получить точное решение на заданном отрезке.

График для третьего примера:

Эйлер      Эйлер-Коши      Рунге-Кутта      Эталон

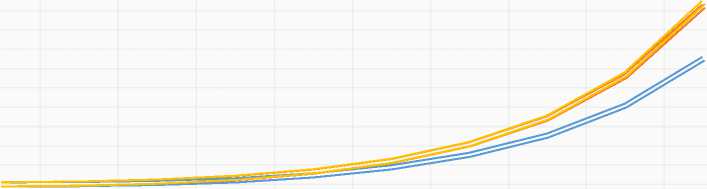
3,2000 3,0000 2,8000 2,6000 2,4000 2,2000 2,0000 1,8000 1,6000 1,4000 1,2000 1,0000 0,8000 0,6000 0,4000 0,2000 0,0000

1,0000 1,0030 1,0150 1,0425 1,0927 1,1754 1,3051 1,5052 1,8152 2,3041

В данном примере можно увидеть достаточную эффективность метода Эйлера-Коши.

Для более точного определения эффективности рассматриваемых методов следует также провести анализ времени их работы, что может быть крайне полезно при разработке программ, предназначенных для обработки и решения достаточно большого количества задач Коши различной сложности.

Итак, время работы метода зависит от программного окружения, то есть от общей загруженности системы. Среднее значение времени выполнения методов в наносекундах представлено на диаграмме:

Время выполнения

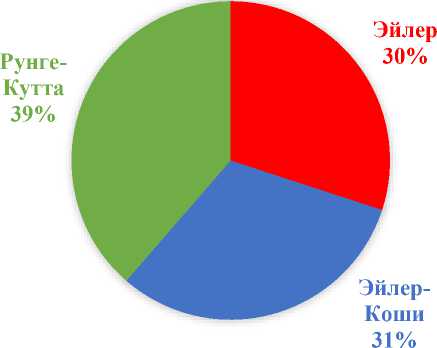
Сравнительно с другими языками программирования описанные методы в Java отрабатывают за немного большее время, что обусловлено также имеющимся в коде синтаксическим анализатором функций.

Вывод:

После проведенного исследования выявлено, что метод Рунге-Кутта обладает более высокой точностью, но имеет наибольшее время выполнения, однако для некоторых видов задач эффективны может быть и метод Эйлера, имеющего наименьшую точность и самую высокую скорость выполнения. Можно сделать вывод, что при выборе метода решения задачи Коши следует опираться на конкретную задачу и на ожидаемую точность решения. Если же требуется разработать собственную программу для решения задачи Коши одним из приведенных численных методов, при выборе метода следует учитывать сложность реализации и особенности языка программирования.