Анализ эффективности способов спецификации уравнения регрессии

Автор: Моисеев Никита Александрович, Романников Александр Николаевич

Журнал: Экономический журнал @economicarggu

Статья в выпуске: 1 (45), 2017 года.

Бесплатный доступ

В данной статье представлен сравнительный анализ способов спецификации линейного регрессионного уравнения посредством проведения серии машинных экспериментов. Тестируются такие методы отбора переменных как прямой отбор, пошаговый отбор, обратное исключение, отбор по остаточной корреляции, лучшие подмножества и все возможные комбинации. В качестве критерия эффективности модели сравниваются такие показатели как средняя квадратичная ожидаемая ошибка прогноза, Байесовский информационный критерий, F-статистика и дисперсия бутстрапированных ошибок. В результате проведенных экспериментов делаются выводы и даются рекомендации относительно оптимальности применимости того или иного способа спецификации, а также критерия эффективности модели при различных параметрах исследуемых наборов данных.

Еще

Спецификация регрессии, линейная модель, метод наименьших квадратов, байесовский информационный критерий, f-статистика

Короткий адрес: https://sciup.org/14915315

IDR: 14915315

Текст научной статьи Анализ эффективности способов спецификации уравнения регрессии

Moiseyev Nikita, Romannikov Alexander

ANALYSIS OF EFFICIENCY OF WAYSOF THE SPECIFICATION OF THE EQUATION OF REGRESSION

В настоящее время самым широко распространенным методом вычисления коэффициентов регрессионной модели является метод наименьших квадратов (МНК, англ. Ordinary Least Squares) и его многочисленные вариации. В связи с этим постараемся в данной статье глубже разобраться в его специфике, достоинствах, недостатках и способах их устранения. Для начала дадим небольшую справку по данному методу.

МНК является математическим методом поиска оптимальных параметров регрессионной модели, основанный на минимизации суммы квадратов отклонений подстраиваемой функции от истинных значений целевой переменной. Пусть { Y, X }– рассматриваемая выборка статистических данных, где Y – вектор-столбец наблюдений значений целевой переменной размерностью n × 1, а X – конечная матрица наблюдений по объясняющим переменным размерностью n × ( m + 1).

X = 1

x ₁₁

x 21

1 x n 1

x ₁ _m

x 2 m

, Y =

y ₁

y ₂

X nm

y_n

Тогда линейная регрессионная модель может быть представлена в следующем виде:

У. = b 0 + b l xt 1 + b 2 xt 2 + - + bmxm + et, либо в матричной форме: ^^

где e – вектор-столбец ошибок модели, состоящий из элементов .

Для нахождения вектора коэффициентов проводится процедура нахождения минимума целевой функции, представляющей собой сумму квадратов отклонений модельных значений от истинных значений целевой переменной. В результате данной оптимизации вектор выражается аналитически следующим образом:

B = ( X T X )^- ¹ X T Y .

Здесь необходимо отметить, что МНК заслужил свою популярность, поскольку полученные на его основе оценки истинных коэффициентов регрессии β являются лучшими несмещенными оценками из класса линейных оценок (англ. BLUE, Best Linear Unbiased Estimator) при выполнении указанных ниже предпосылок.

Предпосылка 1: Строгая экзогенность ошибок, т. е. E ( ε_t | X ). Это значит, что ошибки модели не зависят от объясняющих переменных;

Предпосылка 2: Гомоскедастичность ошибок, т. е. E ( ε_t ² | X ) = σ ² . Дисперсия случайных отклонений является константой и не зависит от величины значений объясняющих переменных. Отметим, что невыполнение этой предпосылки называется гетероскедастичностью;

Предпосылка 3: Нормальность ошибок, т. е. ε_t ~ N (0; σ ). Случайные отклонения истинных значений зависимой переменной от модельных подчиняются нормальному распределению с нулевым математическим ожиданием и некоторой дисперсией;

Предпосылка 4: Отсутствие полной мультиколлинеарности, т. е. X ^ТX является положительно определенной матрицей. Здесь имеется ввиду, что среди объясняющих переменных нет функциональной линейной связи;

Предпосылка 5: Отсутствие автокорреляции остатков, т. е. сov( ε_i ; ε j ) = 0, i ≠ j . Случайные отклонения являются полностью независимыми друг от друга, что означает отсутствие систематической взаимосвязи между любыми отдельно взятыми ошибками модели.

На практике при построении модели зачастую приходится прибегать к процедуре отбора объясняющих переменных, иначе называемой спецификацией модели. При проведении спецификации мы стремимся отобрать для расчета коэффициентов линии регрессии наиболее значимые предикторы и исключить незначимые, т.е. те, которые не оказывают влияния на целевую переменную. Следует отметить, что качество проведенной спецификации оказывает существенное влияние на эффективность и адекватность получаемой модели. Именно поэтому в данной статье мы сконцентрируемся на тестировании и сравнительном анализе различных способов отбора и интегрирования набора объясняющих переменных. Первым делом дадим краткую информационную справку по наиболее популярным методам спецификации уравнения регрессии.

Отбор по всем возможным комбинациям. В данном случае рассматриваются и сравниваются между собой все возможные модели, которые можно составить из данного набора потенциальных объясняющих переменных. Преимущество этого способа заключается в том, что отсутствует риск упустить лучшую по выбранному критерию модель. Однако указанное преимущество сопряжено с существенным недостатком, которым является вычислительная трудоемкость такого отбора, особенно, если число потенциальных объясняющих переменных достаточно велико. Поскольку количество моделей, которые можно построить по набору из независимых переменных вычисляется по формуле , то уже при 30–40 независимых переменных такой способ отбора модели становится абсолютно нецелесообразным, особенно для персональных компьютеров.

Следует также отметить, что независимо от метода отбора переменных в модель исследователю необходимо определиться с критерием, отражающим качество уравнения регрессии, и согласно которому будет оцениваться та или иная спецификация модели. Несомненно, конечная цель, которую желает достигнуть любой исследователь – это построение модели с минимальной ошибкой прогноза. Однако проблема заключается в том, что нам неизвестно заранее какую ошибку даст рассматриваемая модель. Но существует множество способов получить некоторую оценку будущей эффективности анализируемого уравнения. Приведем несколько самых часто используемых из них.

F-статистика. Отражает отношение суммы квадратов отклонений линии регрессии от среднего значения целевой переменной, деленой на число включенных в уравнение независимых переменных, и несмещенной оценки дисперсии остатков модели. При выполнении гипотезы о том, что истинная линия регрессии не объясняет никаких отклонений целевой переменной от своей средней, F-статистика подчиняется распределению Фишера, а именно

К y - y )2f = ----- n

К У - У )2

I = 1

n - m -1

F m , n

- m - 1^.

Таким образом, согласно данному критерию следует выбрать ту спецификацию, которая дает наибольшее значение F-статистики.

Несмещенная оценка дисперсии ошибок прогноза (англ. Mean Squared Forecast Error, MSFE). Является показателем ожидаемой точности прогноза выбранной модели. Рассчитывается по формуле:

MSFEt+i = s2 (1 + XL (XTX)-1 Xt+i), (5)

где X_t+i – вектор-столбец значений объясняющих переменных, участвующих в построении прогноза на период t + i , s ² – несмещенная оценка дисперсии ошибок, рассчитывающаяся следующим образом:

Z( y — y )2

5 ² = ^-------- . (6)

n — m — 1

Отметим, что формула (5) используется в случае, если известен вектор-столбец X _t+i . В противном случае качество модели оценивается по формуле (6). Разумеется, выбирается та модель, у которой значение несмещенной оценки дисперсии ошибок наименьшее.

Байесовский информационный критерий (англ. Bayesian Information Criterion, BIC). Строится на предположении, что среди рассматриваемого набора моделей имеется одна истинная, которую можно определить с некоторой долей вероятности. Критерий штрафует модели за неоправданно большое количество параметров, тем самым, предотвращая переобучение модели. Вычисляется как:

BIC = n ■ In ( 5 ²) + m ■ In ( n ) . (7)

Предпочтение отдается той модели, у которой значение байесовского информационного критерия является наименьшим.

Информационный критерий Акаике (англ. Akaike Information Criterion, AIC). Является очень близким по смыслу с байесовским информационным критерием, так как также накладывает на модель штраф за каждую включаемую объясняющую переменную. Рассчитывается следующим образом:

AIC = n ■ In (52) + 2m. (8)

Выбирается точно так же, как и в предыдущем случае та модель, у которой значение информационного критерия является наименьшим.

Бутстрап (англ. Bootstrap). В основе бутсраповского подхода лежит идея, что истинное распределение данных можно с достаточной точностью приблизить эмпирическим, то есть теми данными, которые оказались в выборке. В данном случае нам необходимо оценить качество рассматриваемой модели, а именно ее ожидаемую ошибку прогноза. Для этого можно прибегнуть к одной из бутстраповских техник “one in – one out”. Допустим имеется окно наблюдений размера и по этой выборке оценивается дисперсия ошибок линейной регрессионной модели. Начинается данная процедура с того, что из выборки удаляется первая строчка, характеризующая значения переменных по одному наблюдению, и без нее рассчитываются параметры уравнения регрессии. Затем с помощью полученных параметров делается прогноз для удаленного ранее значения целевой переменной и записывается полученная ошибка. Далее удаленная строчка возвращается в выборку, удаляется вторая строчка и процедура повторяется. По проведении итераций рассчитывается оценка дисперсии ошибок модели по формуле:

L (~ - y)

i =1 _______________

В данном случае волна над символами обозначает, что данные значения мы получили по результатам бутстрапированной выборки.

Прямой отбор (англ. Forward Selection). Данный алгоритм предполагает выполнение следующих пошаговых операций. На первой стадии из всех имеющихся объясняющих переменных выбирается та, которая имеет наибольший показатель корреляции с целевой переменной. Далее по полученной модели рассчитывается один из показателей ее эффективности, рассмотренных выше. Затем к модели по очереди добавляются оставшиеся независимые переменные и пересчитывается выбранный ранее показатель эффективности. После чего в модель вводится переменная, вызвавшая наибольшее улучшение качества модели. Процедура повторяется до тех пор, пока ни одна из переменных более не улучшает показатель эффективности регрессионного уравнения.

Обратное исключение (англ. Backward Elimination). Данный способ спецификации регрессионного уравнения схож с предыдущим с той лишь разницей, что изначально в уравнение включаются все возможные переменные (в случае, если их число не превышает число наблюдений) и затем происходит постепенное отсеивание незначимых факторов. На каждом шаге мы попеременно исключаем из уравнения все имеющиеся переменные и сравниваем получившиеся модели плюс модель без исключения переменной по приведенным выше показателям эффективности.

В результате проведенных сравнений принимается решение о целесообразности исключения объясняющей переменной из уравнения. Процедура завершается в случае, если исключение любого фактора ведет к потере качества модели.

Пошаговый отбор (англ. Stepwise selection). Представляет собой всего лишь модификацию метода прямого отбора. Различие в данном случае заключается в том, что на каждом шаге после включения в уравнение нового фактора производится проверка на значимость всех уже имеющихся переменных модели. Обычно значимость предикторов модели характеризуется p-значением, которое в классической литературе предлагается рассчитывать согласно следующей формуле:

p_t = ² •

¹ T n - m -1

b i

V V Var (bi)

В данном случае T_n–m–1 (x) – интегральная функция распределения Стьюдента с числом степеней свободы n – m – 1 , а несмещенная оценка дисперсии коэффициентов вычисляется как:

Var (bi-i ) = ?(XTX) — 1.

Если в процессе такой проверки обнаружится, что какие-то переменные стали незначимыми в уравнении, то они выводятся из модели, после чего начинается очередная итерация по поиску новой переменной, способной улучшить качество модели.

Лучшие подмножества (англ. Best Subsets). Данный способ спецификации регрессионного уравнения является частным случаем отбора по всем возможным комбинациям. Здесь исследователь заранее определяет максимальное количество предикторов в уравнении. После чего перебираются все возможные комбинации объясняющих переменных, удовлетворяющих установленному ограничению на количество. Полученные модели сравниваются между собой по одному из показателей эффективности, рассмотренных выше, и выбирается лучшая из них.

Отбор по остаточной корреляции. Идея метода заключается в следующем. На первом этапе определяется объясняющая переменная, имеющая наибольшую корреляцию с целевой. Затем в модель добавляется следующая переменная, которая показывает наиболее тесную связь с остатками модели, построенной только по первой включенной переменной. Для нахождения этой объясняющей переменной будем использовать частный коэффициент корреляции, который отражает взаимосвязь между двумя переменными, «очищенными» от влияния других переменных. Частный коэффициент корреляции между переменными i и j , «очищенными» от влияния остальных факторов набора из переменных, в общем виде вычисляется как показано ниже:

r j .12. .( I -1 )( I + 1 ) . ( j -1 )( j + 1 ) . k

R ^-

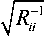
• R

где – R _i j ^–1 i -ый j -ый элемент обратной корреляционной матрицы, включающей весь набор из k переменных.

Таким образом, для того, чтобы включить в модель вторую переменную, необходимо рассчитать частные корреляции всех оставшихся факторов с зависимой переменной, «очищенные» от влияния первой переменной. Для включения третьей переменной в модель повторяется та же самая процедура, только частные корреляции рассчитываются уже с учетом двух включенных ранее предикторов. На каждом шаге полученные модели проверяются согласно выбранному показателю эффективности. Процедура повторяется до тех пор, пока включение новых переменных перестает повышать качество модели.

Рассмотренные выше способы за исключением самого первого призваны снизить вычислительную сложность процедуры спецификации регрессионного уравнения и при этом минимизировать риски упущения из рассмотрения наилучшей модели, которую можно построить по данному набору независимых переменных. В данной статье мы постараемся проанализировать эффективность применения этих способов в зависимости от свойств и структуры набора потенциальных объясняющих переменных и дать рекомендации относительно их применимости в тех или иных ситуациях.

Предположим имеется целевая переменнаяи набор потенциальных объясняющих переменных x_t ₁, x_t ₂, …, x_tm . Для проведения сравнительного анализа вышеописанных способов спецификации поставим несколько имитационных экспериментов. В данных экспериментах будем полагать, что объясняющие переменные подчиняются нормальному распределению с нулевой средней и единичной дисперсией, а именно x_t ₁, x_t ₂, …, x_tm ~ N [ E ( x_ti ) = 0, D ( x_ti ) = 1].Также на данном этапе установим, что объясняющие переменные не мультиколлинеарны, то есть являются линейно независимыми друг от друга. Определим, что целевая переменная зависит только от первых четырех предикторов из сгенерированного набора данных, а остальные факторы не имеют никакой взаимосвязи с y_t . Таким образом, y_t будет вычисляться как:

У. = 2 + S“ xi + et, (13) i =1 i где εt~N(0,1) – «белый» шум, 2 – произвольно выбранная константа модели, βi = 1/i – истинные коэффициенты модели, убывающие пропорционально порядковому номеру объясняющей переменной.

В результате проведенного имитационного эксперимента были протестированы все шесть представленных выше способов отбора переменных, а именно отбор по всем возможным комбинациям, лучшие подмножества с числом включаемых переменных l ≤ 4, прямой отбор, пошаговый отбор с уровнем значимости sig < 0.05, отбор по остаточной корреляции и обратное исключение. Данные способы были реализованы с использованием следующих критериев качества модели: несмещенная оценка дисперсии ошибок прогноза (MSE), F-статистика, Байесовский информационный критерий (BIC), среднеквадратичные бутстрапированные ошибки модели. Для сравнения эффективности и особенностей применения каждого из методов отбора переменных и критериев качества использовались: среднеквадратичная ошибка прогноза за пределами выборки (MSE) и эмпирическая вероятность включения i -ого предиктора в модель (w _i ).

Эксперимент включал в себя несколько планов, при которых проверялись вышеупомянутые способы спецификации уравнения и критерии качества модели при трех различных окнах данных n = 20, n = 40, n = 80, а также при разном количестве потенциальных объясняющих переменных m = 4, m = 6, m = 9. Для получения расчетных значений по каждому из способов спецификации использовалось 10 000 итераций.

В таблице 1 представлена сводка по эффективности способов отбора переменных при критерии качества MSE и количестве потенциальных объясняющих переменных равном четырем. Таким образом, согласно (13) в исходном наборе предикторов содержатся только переменные, которые действительно оказывают влияние на результирующую переменную. Данная ситуация возникает, когда исследователь корректно идентифицировал теоретические взаимосвязи изучаемых экономических процессов и отобрал в пул переменных значимые факторы.

Таблица 1. Сравнение методов спецификации уравнения регрессии по критерию MSE, m = 4

		s s CT cd s VO 2 s m	СУ m s g _ 3 2 -» ^ G	VO о )G О S’	о to •&>	о S	О G G G О s
20	MSE	1.412245	1.412245	1.413594	1.500384	1.412343	1.414995
	w1	0.8342	0.8342	0.8289	0.589	0.8286	0.832
	w2	0.6536	0.6536	0.6479	0.3266	0.6392	0.6524
	w3	0.5434	0.5434	0.5349	0.2241	0.5428	0.5434
	w4	0.4837	0.4837	0.4774	0.1691	0.4726	0.4836
40	MSE	1.180281	1.180281	1.181057	1.274298	1.180361	1.186613
	w1	0.9685	0.9685	0.9678	0.8279	0.9681	0.9683
	w2	0.8356	0.8356	0.8334	0.4911	0.8326	0.8355
	w3	0.6989	0.6989	0.6962	0.3104	0.6878	0.6961
	w4	0.6024	0.6024	0.6007	0.2212	0.5986	0.6011
80	MSE	1.073722	1.073722	1.073726	1.126084	1.075344	1.07856
	w1	0.9993	0.9993	0.9993	0.9815	0.9994	0.9987
	w2	0.964	0.964	0.9638	0.7989	0.964	0.9682
	w3	0.8738	0.8738	0.8737	0.5583	0.8725	0.8759
	w4	0.7696	0.7696	0.7696	0.3893	0.7689	0.7695

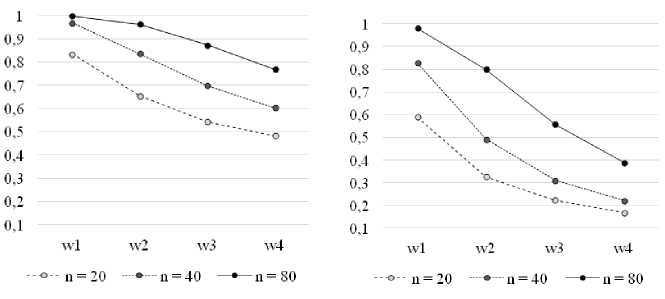
Риc. 1а. Частотность включения Риc. 1б. Частотность включения факторов в модель (отбор по всем факторов в модель (пошаговый отбор, комбинациям, критерий MSE, m = 4) критерий MSE, m = 4)

По таблице 1 можно отследить, как с ростом числа наблюдений спецификации моделей все чаще совпадают с истинной. Также, анализируя показатель MSE по разным способам спецификации, становится ясно, что в случае, если набор потенциальных предикторов совпадает с истинным, метод пошагового отбора с контролем уровня значимости не является предпочтительным. В данном случае при процедуре спецификации уравнения желательным является включение как можно большего числа факторов, поскольку все они влияют на целевую переменную. Пошаговый отбор с этой точки зрения является достаточно «строгим» методом спецификации, так как включает в уравнение только те предикторы, которые с высокой степенью уверенности влияют на зависимую переменную, таким образом теряя в точности прогнозирования.

Для иллюстрации вышесказанного на рисунках 1а и 1б приведены вероятности включения потенциальных факторов в уравнение при способе отбора по всем возможным комбинациям и пошаговом отборе. Как видно, из этих рисунков при пошаговом отборе гораздо меньшее количество переменных в среднем включается в уравнение, что в данном случае ведет к потере точности прогноза, так как на самом деле все потенциальные предикторы являются значимыми.

Как видно из таблицы 2 пошаговый отбор уже не является явным аутсайдером по точности прогноза, в случае, если в рассматриваемом наборе предикторов появилось два, никак не связанных с целевой переменной.

На рисунках 2а и 2б видно, что переменные №5 и №6, не влияющие на целевую переменную гораздо реже включаются в уравнение регрессии, особенно при большом количестве наблюдений. Однако, в случае отбора

Таблица 2. Сравнение методов спецификации уравнения регрессии по критерию MSE, m = 6

s s CT cd s VO 2 s m cd G ^ VO о )G C m о £ о g o’ У 5 vo .bo П S S s О S G О s 20 MSE 1.595099 1.584214 1.581305 1.548723 1.575332 1.580023 w1 0.8167 0.8055 0.8096 0.5574 0.8133 0.8261 w2 0.6387 0.6194 0.6276 0.2998 0.635 0.6543 w3 0.5392 0.5137 0.5255 0.1998 0.5375 0.5544 w4 0.4848 0.4585 0.4693 0.1604 0.4705 0.5093 w5 0.3748 0.3349 0.3642 0.0862 0.3542 0.3878 w6 0.3692 0.3343 0.3575 0.0804 0.3508 0.3718 40 MSE 1.225285 1.223898 1.226202 1.300612 1.229469 1.230168 w1 0.9639 0.9561 0.9625 0.8159 0.963 0.9669 w2 0.828 0.8027 0.825 0.484 0.8184 0.8326 w3 0.6889 0.6483 0.6836 0.3055 0.6819 0.6888 w4 0.6002 0.5488 0.5944 0.2195 0.5804 0.602 w5 0.3365 0.2603 0.3328 0.0578 0.3402 0.3378 w6 0.3342 0.2676 0.3312 0.0577 0.3318 0.349 80 MSE 1.104427 1.102402 1.104555 1.135791 1.106067 1.095833 w1 0.9991 0.9982 0.999 0.9793 0.9986 0.9991 w2 0.969 0.9497 0.9687 0.8058 0.9625 0.9682 w3 0.8743 0.8214 0.8729 0.5597 0.871 0.8712 w4 0.7632 0.6875 0.7617 0.3999 0.7647 0.7708 w5 0.32 0.1703 0.3179 0.0522 0.3243 0.3248 w6 0.3218 0.1729 0.32 0.05 0.3261 0.3293 по всем возможным комбинациям незначимые предикторы включаются чаще, чем при пошаговом отборе (35-40% против 5-10%). Но при этом в случае пошагового отбора менее вероятно и включение значимых факторов, что в общем и целом приводит примерно к равной точности прогнозирования.

Таблица 3. Сравнение методов спецификации уравнения регрессии по критерию MSE, m = 9

		s s a s VO S m	cy m о i s g 3 2 -» A В ^	о VO о >S о S’	о VO о >s E О § ^vо .&) П ^	о §	о m S f О s
1	2	3	4	5	6	7	8
20	MSE	1.980721	1.836345	1.895016	1.631747	1.838751	2.01023
	w1	0.7938	0.7495	0.7974	0.5238	0.7935	0.7965
	w2	0.6377	0.5614	0.6286	0.2821	0.6148	0.6482
	w3	0.554	0.4573	0.531	0.1873	0.528	0.5664
	w4	0.5008	0.3997	0.4762	0.1471	0.4871	0.5114
	w5	0.4102	0.2868	0.3784	0.0743	0.3731	0.4261
	w6	0.4007	0.2898	0.371	0.0791	0.3805	0.4316
	w7	0.4053	0.2892	0.3772	0.0764	0.3763	0.4271
	w8	0.4084	0.2894	0.3771	0.0783	0.3696	0.4375
	w9	0.4056	0.2836	0.3754	0.0748	0.3764	0.4283

Продолжение талб. 3

1	2	3	4	5	6	7	8
40	MSE	1.334179	1.312947	1.330512	1.324853	1.353906	1.353566
	w1	0.9563	0.9322	0.9556	0.7987	0.9552	0.9634
	w2	0.8147	0.7407	0.8104	0.4722	0.8133	0.8222
	w3	0.6787	0.5774	0.672	0.2931	0.6743	0.6835
	w4	0.5897	0.4693	0.5817	0.2113	0.5812	0.5887
	w5	0.34	0.2099	0.3299	0.0567	0.338	0.358
	w6	0.347	0.2118	0.3364	0.0561	0.3468	0.3607
	w7	0.3382	0.2028	0.3283	0.577	0.3491	0.3366
	w8	0.341	0.2096	0.3326	0.0601	0.3286	0.3252
	w9	0.3543	0.222	0.3444	0.0588	0.3387	0.322
80	MSE	1.109306	1.107999	1.110039	1.130571	1.129652	1.099458
	w1	0.9987	0.9944	0.9987	0.9805	0.9987	0.9982
	w2	0.9599	0.9113	0.959	0.7907	0.9625	0.9593
	w3	0.863	0.7537	0.8625	0.5555	0.8602	0.8518
	w4	0.7694	0.6079	0.7666	0.397	0.7556	0.7319
	w5	0.3297	0.1327	0.326	0.0501	0.317	0.3008
	w6	0.3382	0.1403	0.3342	0.0535	0.3297	0.3301
	w7	0.3307	0.1316	0.3266	0.048	0.3249	0.3152
	w8	0.3282	0.1279	0.3243	0.0495	0.3283	0.3296
	w9	0.3218	0.1293	0.318	0.0491	0.3203	0.3194

На рисунках 3а и 3б представлена схожая картина, как и на рисунках 2а, 2б с той лишь разницей, что в данном случае количество незначимых предикторов в изначальном наборе факторов увеличилось до пяти. Как видно из таблицы 3 в случае малого количества наблюдений и при значительном числе незначимых предикторов контроль уровня значимости в некоторой мере оправдывает себя.

В таблицах 4–6 представлены сводки по эффективности способов отбора переменных по байесовскому информационному критерию. Рассматриваются аналогичные случаи как в таблицах 1-3, а именно три различных окна данных , а также количество потенциальных объясняющих переменных .

Таблица 4. Сравнение методов спецификации уравнения регрессии по критерию BIC, m = 4

		s CT cd s VO О Ч о о m S	СУ ^ G ^	О VO о )G О К	m о г о g о У п ё	в ст о S	G О И О s
1	2	3	4	5	6	7	8
20	MSE	1.457402	1.457402	1.457319	1.457673	1.423258	1.471792
	w1	0.6304	0.6304	0.6206	0.6203	0.6116	0.6387
	w2	0.3521	0.3521	0.3408	0.3404	0.3492	0.3664
	w3	0.2498	0.2498	0.2396	0.2394	0.2428	0.26
	w4	0.2077	0.2077	0.2	0.2	0.1848	0.2125
40	MSE	1.298385	1.298385	1.301812	1.301753	1.291321	1.299321
	w1	0.8105	0.8105	0.8044	0.8044	0.8015	0.8145
	w2	0.4537	0.4537	0.4443	0.4443	0.4454	0.4628
	w3	0.2805	0.2805	0.2713	0.2712	0.2763	0.2723
	w4	0.194	0.194	0.1873	0.1872	0.1871	0.1934

Продолжение талб. 4

80	MSE	1.13961	1.13961	1.143122	1.143115	1.12843	1.14121
	w1	0.9695	0.9695	0.9665	0.9665	0.9676	0.9697
	w2	0.7038	0.7038	0.6964	0.6964	0.6912	0.7032
	w3	0.4495	0.4495	0.4429	0.4428	0.433	0.4446
	w4	0.2826	0.2826	0.2762	0.2762	0.284	0.2797

Таблица 5. Сравнение методов спецификации уравнения регрессии по критерию BIC, m = 6

		s s CT cd s VO ° о m S	СУ	О VO о >s о с	5 ю .ьо п	в ст о S	S О s
20	MSE	1.531847	1.533302	1.523368	1.517422	1.540227	1.581985
	w1	0.5972	0.5964	0.5829	0.5605	0.5843	0.6188
	w2	0.3491	0.3481	0.3338	0.3047	0.3351	0.3658
	w3	0.2428	0.2415	0.2255	0.1994	0.2289	0.2692
	w4	0.1976	0.1956	0.1815	0.1591	0.1789	0.2149
	w5	0.1095	0.1075	0.0991	0.0837	0.0999	0.1261
	w6	0.1079	0.1067	0.0981	0.0845	0.0986	0.1209
40	MSE	1.287326	1.28761	1.290412	1.290811	1.311268	1.273256
	w1	0.8039	0.8036	0.7933	0.7932	0.784	0.8153
	w2	0.472	0.4715	0.4572	0.4567	0.4457	0.4675
	w3	0.2804	0.2797	0.266	0.2656	0.2686	0.2982
	w4	0.1946	0.1939	0.1849	0.1845	0.1826	0.2083
	w5	0.0509	0.0502	0.0476	0.0475	0.0466	0.0532
	w6	0.0548	0.054	0.0508	0.0503	0.0475	0.0541
80	MSE	1.171932	1.172059	1.174377	1.174377	1.170231	1.15699
	w1	0.968	0.9679	0.9652	0.9652	0.9645	0.9694
	w2	0.7061	0.7058	0.6977	0.6977	0.6905	0.7079
	w3	0.4356	0.435	0.4286	0.4286	0.4324	0.4447
	w4	0.2812	0.2803	0.2731	0.2731	0.2799	0.299
	w5	0.0242	0.0228	0.0235	0.0235	0.0246	0.0287
	w6	0.0266	0.025	0.0251	0.0251	0.0246	0.0289

Таблица 6. Сравнение методов спецификации уравнения регрессии по критерию BIC, m = 9

		s s CT cd s VO О ° о	СУ s g 3 2 -» Д § X'	CT О VO о )G CT	3 ° У	o S	G О G О s
20	MSE	1.694907	1.678955	1.644776	1.629418	1.66095	1.769303
	w1	0.5844	0.5801	0.5593	0.5337	0.5547	0.5963
	w2	0.3463	0.3397	0.3154	0.2832	0.3097	0.3761
	w3	0.2595	0.2519	0.2257	0.1933	0.2093	0.2842
	w4	0.198	0.1908	0.1678	0.1428	0.1669	0.2412
	w5	0.1228	0.1156	0.0992	0.0793	0.0979	0.1398
	w6	0.1184	0.1101	0.096	0.0769	0.093	0.1454
	w7	0.1169	0.1079	0.0954	0.0755	0.0859	0.1526
	w8	0.1123	0.1045	0.0912	0.0733	0.0955	0.1481
	w9	0.1165	0.1084	0.0953	0.0768	0.0968	0.1511
40	MSE	1.352114	1.351788	1.353341	1.353927	1.348325	1.348503
	w1	0.7894	0.7888	0.7791	0.7786	0.7826	0.7996
	w2	0.4522	0.4506	0.4337	0.433	0.4373	0.4812
	w3	0.2876	0.2855	0.2718	0.2715	0.2575	0.295
	w4	0.1916	0.1889	0.1791	0.1787	0.1813	0.2084
	w5	0.0498	0.0485	0.046	0.0456	0.0482	0.0595
	w6	0.051	0.0487	0.0468	0.046	0.045	0.0565
	w7	0.0521	0.0496	0.0452	0.0449	0.0475	0.0543
	w8	0.0516	0.0491	0.0463	0.0461	0.0502	0.0577
	w9	0.0517	0.0502	0.0476	0.0475	0.0467	0.0589
80	MSE	1.171273	1.170671	1.170224	1.170378	1.152341	1.186376
	w1	0.9634	0.9631	0.96	0.96	0.9619	0.9649
	w2	0.7021	0.7002	0.6907	0.6906	0.6923	0.7013
	w3	0.4385	0.4363	0.4259	0.4258	0.4347	0.4563
	w4	0.2836	0.2803	0.2742	0.274	0.2798	0.3048
	w5	0.0273	0.0242	0.0247	0.0246	0.0224	0.0276
	w6	0.0292	0.0269	0.0281	0.028	0.0271	0.032
	w7	0.0269	0.0245	0.0254	0.0254	0.0255	0.0275
	w8	0.0299	0.0278	0.0289	0.029	0.0264	0.0284
	w9	0.0259	0.0242	0.0243	0.0243	0.0255	0.0289

Отметим, что в случае применения байесовского информационного критерия, рассматриваемые способы отбора переменных показывают более близкие результаты, чем при критерии MSE. Сравнивая таблицы 1–3 и 4–6 можно сделать вывод, что применение BIC дает лучшие результаты в случае короткого окна данных, однако при достаточном числе наблюдений предпочтительным остается выбор в пользу критерия наименьшей ожидаемой ошибки прогноза.

Далее в таблицах 7–9 представлены сводки по эффективности способов отбора переменных по критерию F-статистика. Тестирование проводилось по параметрам, аналогичным тем, которые использовались для расчета таблиц 1–6.

Таблица 7. Сравнение методов спецификации уравнения регрессии по критерию F-статистика, m = 4

		s s CT cd s VO О ° о m S	cd m Д § X' ^ G ^	VO о )G О § П	g o’ У с ёа	S s О S	О s
20	MSE	1.458661	1.458661	1.457826	1.463198	1.462404	1.480975
	w1	0.614	0.614	0.5992	0.5668	0.6052	0.6453
	w2	0.3308	0.3308	0.3148	0.2852	0.3171	0.3525
	w3	0.2304	0.2304	0.2176	0.1941	0.2119	0.2463
	w4	0.1771	0.1771	0.1669	0.1479	0.1652	0.1935
40	MSE	1.345871	1.345871	1.346792	1.350051	1.321607	1.324561
	w1	0.7318	0.7318	0.721	0.714	0.7208	0.7586
	w2	0.3056	0.3056	0.2925	0.2861	0.2928	0.3278
	w3	0.171	0.171	0.1607	0.1551	0.1605	0.1897
	w4	0.1082	0.1082	0.1005	0.0961	0.106	0.1268
80	MSE	1.238926	1.238926	1.239607	1.239875	1.275889	1.229155
	w1	0.8646	0.8646	0.8572	0.8569	0.847	0.8708
	w2	0.2617	0.2617	0.2526	0.2522	0.2491	0.2848
	w3	0.1051	0.1051	0.0975	0.0972	0.1049	0.1265
	w4	0.0545	0.0545	0.0506	0.0505	0.052	0.0741

Таблица 8. Сравнение методов спецификации уравнения регрессии по критерию F-статистика, m = 6

20	MSE	1.534856	1.53456	1.51584	1.512927	1.564458	1.565908
	w1	0.5749	0.5741	0.5557	0.5303	0.5592	0.6203
	w2	0.3138	0.3129	0.2894	0.2611	0.2805	0.3559
	w3	0.2167	0.2153	0.1933	0.1726	0.1927	0.26
	w4	0.1744	0.1724	0.153	0.1338	0.1537	0.2116
	w5	0.0876	0.0858	0.0748	0.0636	0.0788	0.1341
	w6	0.0912	0.0898	0.0791	0.0676	0.0857	0.1296
40	MSE	1.36197	1.361627	1.354005	1.365254	1.326859	1.32849
	w1	0.7245	0.7241	0.7114	0.7051	0.7111	0.7411
	w2	0.2969	0.2965	0.2827	0.2771	0.2848	0.3326
	w3	0.1634	0.163	0.1529	0.1485	0.1539	0.1967
	w4	0.1111	0.1103	0.1007	0.0977	0.0957	0.1323
	w5	0.0274	0.0266	0.0233	0.0216	0.0222	0.0346
	w6	0.026	0.0252	0.0239	0.0228	0.024	0.0342
80	MSE	1.261543	1.261543	1.264064	1.263935	1.236504	1.254842
	w1	0.8557	0.8557	0.8468	0.8466	0.8537	0.8731
	w2	0.2626	0.2626	0.2508	0.2506	0.2552	0.2881
	w3	0.111	0.111	0.1016	0.1013	0.1013	0.134
	w4	0.0524	0.0524	0.0485	0.0481	0.0479	0.0715
	w5	0.0036	0.0036	0.0033	0.0031	0.0022	0.004
	w6	0.0026	0.0026	0.0025	0.0025	0.0011	0.0048

Таблица 9. Сравнение методов спецификации уравнения регрессии по критерию F-статистика, m = 9

20	MSE	1.712448	1.682937	1.63928	1.607243	1.616617	1.825362
	w1	0.552	0.545	0.5146	0.4904	0.5166	0.626
	w2	0.3083	0.2972	0.2629	0.243	0.2637	0.3936
	w3	0.2127	0.2026	0.1756	0.1576	0.1766	0.3093
	w4	0.1682	0.1556	0.1316	0.1153	0.1372	0.257
	w5	0.1025	0.0914	0.0735	0.0603	0.0726	0.177
	w6	0.1013	0.0898	0.0725	0.0606	0.0699	0.1814
	w7	0.1049	0.0934	0.0741	0.061	0.0702	0.1821
	w8	0.1003	0.0908	0.0715	0.0572	0.0696	0.1876
	w9	0.1006	0.0902	0.0719	0.0608	0.0765	0.177
40	MSE	1.331854	1.330796	1.337458	1.33891	1.370318	1.368247
	w1	0.7045	0.7032	0.6858	0.6807	0.6834	0.7412
	w2	0.2926	0.2917	0.2746	0.2704	0.2825	0.3363
	w3	0.1666	0.166	0.1549	0.1519	0.1445	0.2015
	w4	0.1035	0.1025	0.0924	0.0891	0.0987	0.1467
	w5	0.0232	0.0222	0.0211	0.0199	0.0218	0.0418
	w6	0.0232	0.0226	0.0198	0.0185	0.022	0.0389
	w7	0.0246	0.0238	0.0218	0.0201	0.0198	0.0424
	w8	0.0248	0.0241	0.0216	0.0197	0.0213	0.0401
	w9	0.0233	0.0225	0.0193	0.0184	0.0223	0.0395
80	MSE	1.219736	1.219682	1.221796	1.221807	1.282559	1.240945
	w1	0.858	0.858	0.8508	0.8507	0.8527	0.8702
	w2	0.2589	0.2588	0.2476	0.2475	0.2482	0.2914
	w3	0.1048	0.1047	0.0962	0.0961	0.0975	0.1378
	w4	0.0554	0.0553	0.0509	0.0507	0.0471	0.0729
	w5	0.0031	0.0029	0.0025	0.0024	0.0024	0.0051
	w6	0.0021	0.0021	0.0016	0.0016	0.0024	0.0047
	w7	0.0028	0.0028	0.0027	0.0027	0.0023	0.0044
	w8	0.0022	0.0022	0.0025	0.0025	0.0022	0.0045
	w9	0.004	0.004	0.0038	0.0038	0.0019	0.0045

Анализируя результаты эффективности способов спецификации регрессионного уравнения из таблиц 7-9, можно заключить, что F-статистика так же как и BIC является менее предпочтительным критерием оценки качества модели, чем MSE в случае длинного окна наблюдений, однако демонстрирует схожую с BIC эффективность при коротком окне данных.

Ниже в таблицах 10-12 приведены результаты имитационного эксперимента по проверке эффективности способов отбора переменных согласно величине бутстрапированных среднеквадратических ошибок модели.

Таблица 10. Сравнение методов спецификации уравнения регрессии по критерию бутстрап, m = 4

		s s CT cd s VO О m S	СУ s g _ 3 2 -» д s x¹	VO о )G О S’	e S её»	G CT ^w о S	G О G G G О s
20	MSE	1.423126	1.423126	1.411576	1.458673	1.435022	1.429975
	w1	0.7256	0.7256	0.7262	0.5899	0.7172	0.7434
	w2	0.4969	0.4969	0.4922	0.3162	0.491	0.5196
	w3	0.3969	0.3969	0.391	0.2234	0.3685	0.4056
	w4	0.3402	0.3402	0.3288	0.1706	0.3088	0.3417
40	MSE	1.205586	1.205586	1.206058	1.268908	1.239423	1.224884
	w1	0.926	0.926	0.9221	0.8258	0.9176	0.9264
	w2	0.704	0.704	0.698	0.493	0.6924	0.7104
	w3	0.5333	0.5333	0.5279	0.3102	0.5182	0.5381
	w4	0.4203	0.4203	0.415	0.2121	0.4062	0.4306
80	MSE	1.115735	1.115735	1.11604	1.15255	1.104863	1.10235
	w1	0.9965	0.9965	0.9962	0.9846	0.9953	0.9955
	w2	0.924	0.924	0.924	0.7922	0.9118	0.9215
	w3	0.7674	0.7674	0.7674	0.5691	0.7677	0.7694
	w4	0.6327	0.6327	0.6327	0.4024	0.6126	0.6189

Таблица 11. Сравнение методов спецификации уравнения регрессии по критерию бутстрап, m = 6

20	MSE	1.577075	1.576173	1.563686	1.532479	1.599864	1.586442
	w1	0.7069	0.7043	0.6999	0.5554	0.6863	0.7162
	w2	0.4992	0.4932	0.4823	0.3019	0.4565	0.5168
	w3	0.3868	0.3802	0.3703	0.2003	0.3479	0.4031
	w4	0.3407	0.3325	0.3206	0.1584	0.2869	0.3574
	w5	0.2321	0.2243	0.2147	0.0826	0.1903	0.2507
	w6	0.2288	0.2197	0.2099	0.0815	0.191	0.2438
40	MSE	1.240247	1.239571	1.241776	1.285424	1.289202	1.240869
	w1	0.9198	0.9172	0.9168	0.8206	0.9105	0.9232
	w2	0.6994	0.6926	0.6913	0.4821	0.6848	0.7074
	w3	0.5343	0.522	0.5248	0.308	0.5067	0.5433
	w4	0.4246	0.408	0.416	0.2104	0.404	0.4339
	w5	0.1934	0.1732	0.1867	0.0599	0.1647	0.1997
	w6	0.1954	0.1786	0.1885	0.0601	0.1654	0.202
80	MSE	1.140508	1.139433	1.140555	1.17063	1.102485	1.140032
	w1	0.9965	0.9953	0.9963	0.981	0.9964	0.9966
	w2	0.9154	0.9053	0.913	0.7931	0.9137	0.9167
	w3	0.7626	0.7413	0.7597	0.5558	0.7645	0.765
	w4	0.615	0.585	0.6125	0.3856	0.6103	0.6168
	w5	0.1793	0.1262	0.176	0.0557	0.1646	0.1811
	w6	0.168	0.1209	0.1668	0.0503	0.1529	0.1696

Таблица 12. Сравнение методов спецификации уравнения регрессии по критерию бутстрап, m = 9

		s s CT cd s VO О ° о	cd m s g Д § X'	VO о )G О § C	>S g o’ У 5 vo .bo П S	S s О S	G G G О s
20	MSE	1.864355	1.816384	1.770326	1.644799	1.696479	1.932457
	w1	0.7024	0.671	0.6913	0.5336	0.6542	0.711
	w2	0.495	0.4604	0.4616	0.2704	0.4343	0.5207
	w3	0.4079	0.3716	0.3705	0.1883	0.3302	0.4397
	w4	0.3482	0.3117	0.3082	0.1388	0.2793	0.3819
	w5	0.2642	0.2206	0.2194	0.0749	0.1834	0.2995
	w6	0.259	0.2204	0.2168	0.0761	0.1833	0.2873
	w7	0.2507	0.2134	0.2054	0.0745	0.1805	0.2869
	w8	0.2702	0.2342	0.2226	0.0804	0.1862	0.3038
	w9	0.2573	0.2207	0.2141	0.0764	0.1855	0.2895
40	MSE	1.288918	1.279112	1.27942	1.281611	1.321003	1.289904
	w1	0.9099	0.8946	0.9086	0.8038	0.901	0.9136
	w2	0.6942	0.666	0.684	0.4802	0.6559	0.7053
	w3	0.5244	0.4872	0.5114	0.299	0.491	0.5336
	w4	0.4252	0.3856	0.4133	0.2126	0.3911	0.4362
	w5	0.196	0.1594	0.1843	0.0607	0.1673	0.2062
	w6	0.1948	0.1591	0.1842	0.0587	0.1697	0.2087
	w7	0.195	0.1598	0.1843	0.057	0.1649	0.206
	w8	0.1941	0.1605	0.1808	0.0548	0.168	0.2058
	w9	0.1917	0.1542	0.1803	0.0545	0.1644	0.2044
80	MSE	1.148844	1.146393	1.147739	1.162737	1.123335	1.149186
	w1	0.9955	0.9917	0.995	0.9816	0.9941	0.9959
	w2	0.9192	0.885	0.9175	0.7976	0.9094	0.9215
	w3	0.7611	0.7037	0.7569	0.569	0.7503	0.7645
	w4	0.6162	0.5436	0.6113	0.3928	0.6096	0.6209
	w5	0.1718	0.1041	0.1671	0.0514	0.1622	0.175
	w6	0.1741	0.1077	0.1697	0.0514	0.1661	0.1783
	w7	0.1738	0.1084	0.1702	0.054	0.1603	0.1787
	w8	0.1714	0.1048	0.1685	0.048	0.1636	0.1745
	w9	0.1726	0.108	0.1681	0.0503	0.1635	0.1762

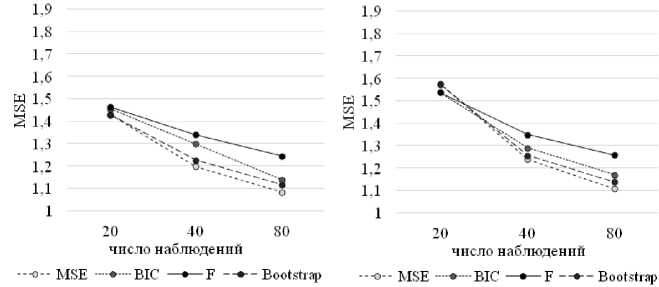
Риc. 4а . Сравнение эффективности моделей ( m = 4)

Риc. 4б . Сравнение эффективности моделей ( m = 6)

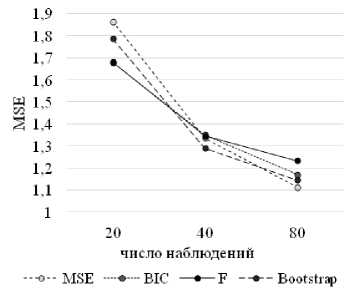
Риc. 4в . Сравнение эффективности моделей ( m = 9)

Модели, полученные на основе критерия бутстрап практически являются аналогом уравнениям, рассчитанным по критерию MSE, демонстрируя слегка большую ошибку при значительном превосходстве числа наблюдений над числом потенциальных предикторов и наоборот – немного более высокую точность при коротком окне данных и значительном числе потенциальных факторов.

На рисунках 4а-4в приведены сравнения средних эффективностей способов спецификации регрессии в зависимости от различных вводных параметров.

Сразу отметим, что ни один из способов спецификации и критериев эффективности не является наиболее предпочтительным при любых исходных условиях. Так, из представленных выше рисунков можно сделать две основные рекомендации: в среднем при значительном превосходстве числа наблюдений над числом рассматриваемых предикторов целесообразней использовать критерий MSE в качестве показателя качества модели, а в случае короткого окна данных и наличия неопределенности относительно значимости отобранных факторов предпочтительнее использовать F-статистику или BIC/AIC. Однако, легко заметить, что, если принимать решение о выборе способа спецификации модели и критерии оценки ее качества в условиях неопределенности относительно степени значимости предварительно отобранных предикторов, то присутствует высокая вероятность выбрать далеко не лучшую модель. Если при достаточно длинном окне данных различия в эффективности способов отбора переменных не такие критичные, то при относительно небольшом числе наблюдений эти различия достигают значений в 20–30% и в этом случае у исследователя появляются реальные риски потери точности из-за неверного выбора способа спецификации и критерия эффективности.

Список литературы Анализ эффективности способов спецификации уравнения регрессии

Moiseev N.A. Linear model averaging by minimizing mean-squared forecast error unbiased estimator. Model Assisted Statistics and Applications. 2016. Т. 11. № 4. С. 325-338.
Zubakin V.A., Kosorukov O.A., Moiseev N.A. Improvement of regression forecasting models. Modern Applied Science. 2015. Т. 9. № 6. С. 344-353.
Бокс, Дж. Анализ временных рядов. Прогноз и управление: пер. с англ./Дж. Бокс, Г. Дженкинс. -М.: Мир, 1974. -Вып. 1. -406 с.; Вып. 2. -198 с.
Глазьев, С. Проблемы прогнозирования макроэкономической динамики/С. Глазьев//Российский экономический журнал. -2001. -№ 3. -С. 76-85; № 4. -С. 12-22.
Крыштановский, А. О. Методы анализа временных рядов/А. О. Крыштановский//Мониторинг общественного мнения: экономические и социальные перемены. -2000. -№ 2 (46). -С. 44-51.
Магнус, Я. Р. Эконометрика. Начальный курс: учебник/Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий. -6-е изд., перераб. и доп. -М.: Дело, 2004. -576 с.
Математическое моделирование экономических процессов. Учебное пособие -М.: Экономика, 1990 -378 с.
Моисеев Н.А. Современные инструментальные методы прогнозирования процессов нестабильной экономики//В сборнике: Международная научно-практическая конференция «Интеграция отечественной науки в мировую: проблемы, тенденции и перспективы» сборник научных докладов. Автономная некоммерческая организация содействия развитию современной отечественной науки Издательский дом «Научное обозрение». 2014. С. 42-54.
Моисеев Н.А., Ахмадеев Б.А. Инновационная модель регрессионного прогноза. Инновации и инвестиции. 2014. № 9. С. 123-127.
Прогнозирование и планирование в условиях рынка: учеб. пособие для вузов/под. ред. Т. Г. Морозовой, А. В. Пикулькина. -2-е изд., перераб. и доп. -М.: ЮНИТИ-ДАНА. 2003. -279 с. -(Серия «Профессиональный учебник: Экономика»).
Эконометрика. Учебник. И.И. Елисеевой. -М.: Финансы и статистика, 2002 -344 с.
Эконометрические методы. Дж. Джонстон. -М.: Статистика, 1980 -444 с.

Еще

Статья научная