Анализ электропривода автономного объекта

В настоящее время электромеханические системы, которые в зависимости от областей применения называются электроприводами, электромеханизмами, электромеханическими устройствами и т.п., все более широко внедряются в новые объекты или области применения, в частности, используются в автономных транспортных средствах, таких как электропогрузчики, электротележки, гольфкары и электромобили. Предлагается использовать в подобных устройствах электропривод на основе вентильного двигателя (ВД). Это позволит повысить надежность устройства, осуществить рекуперацию энергии, в ряде случаев – упростить кинематическую цепь. Рассмотрим возможные варианты управления вентильным двигателем.

В установившемся режиме уравнение механических характеристик для вентильного двигателя описывается формулой [1]:

U cos O = I q Tp + 1) + to (1 - T₃ I d ) ^{- U} sin ⁰ = I d ^(ТЭ p + 1) + ^{to T}3 I q T_M to p = I q - M h

где в относительных единицах представлены следующие координаты: I q и I d – проекции тока на оси d и q во вращающейся системе координат, T M – электромеханическая постоянная времени. На основании системы уравнений (2) можно построить структурную схему двигателя (рис. 1).

„ cos O

M =-- U4^U

—

1 + TU sin 0 ------^э .  . to

1 + Ttoг

,

где М, ω, U, T Э – относительные значения момента, скорости, напряжения и электромагнитной постоянной ВД.

Исходя из (1) управление двигателем может быть реализовано за счет изменения напряжения U либо угла установки θ датчика положения ротора (ДПР). В [1] отмечается, что двигатель может быть описан системой дифференциальных уравнений, которые при переходе к записи в операторной форме принимают вид:

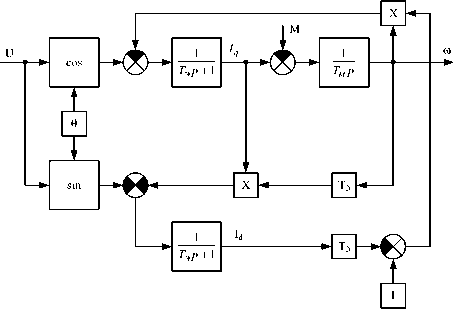
Рис. 1. Структурная схема вентильного двигателя с учетом значения угла установки θ

Из выражения (1) видно, что практически все координаты ВД зависят от угла установки θ . Анализ уравнения (1) показал, что в функции M = f ( θ ) имеется экстремум при условии:

0ЭКС = arctg (-тэ^)

Халиуллов Динар Салаватович, студент

- M

ЭКС     max

ujx + Tto _ to

1 + т Э2 to ²      1 + т Э2 to

Аналогичный анализ можно провести для функции U = f ( θ ). Экстремум U = f ( θ ) достигается при том же условии (3):

U ЭКС

= U min

to        1 + T 2 to ²

-- +—   Э —

V 1 + t 2 ® ²   V 1 + t 2 ®^г

На основании (1) получаем следующее выражение:

Анализ функции ω = f ( θ ) показывает, что экстремум достигается при условии:

U _   (1 - T _Э to0 )U

~ U - to (1 + Т_эи 0 )

T₃M = sin 0 cos 0 + T₃U cos 0

По аналогичной формуле определяется чувствительность к изменению угла установки:

Уравнение (6) не позволяет однозначно, как в предыдущих случаях, определить значение θ ЭКС . Можно найти θ ЭКС для условия М=0:

- (U0 + to + T3Uto)0 U - to(1 + Тэи)0

⁰ ЭКС = arcsin TU )

В этом случае:

_    _ U 1 - T 2² U²

^to ЭКС = ^to max =  ^   Т^Ц¹

.

Сравнение выражений (13) и (14) показывает, что при прочих равных условиях механическая характеристика вентильного двигателя более чувствительна к изменению угла установки ДПР, чем к изменению напряжения. Пусть экстремальный регулятор обеспечивает выполнение условия (3). В этом случае

Для того, чтобы оценить влияние угла установки на момент, найдем приращение ΔМ по формуле:

sin 0 экс = sin( arctg ( — T э to )) =

KM = M_3Kc - M_H

cos 0 экc = cos( arctg ( - T э to )) =

^{- T}э to

>1 1 + т Э 2to ²

V1 + T э²to²

где М ЭКС – экстремальное значение по формуле (4); М Н – значение М по формуле (1) при условии θ =0 (нейтральная установка датчика).

KM =

U Q1 + T э²to ² - 1) 1 + т Э2 ® to

Видно, что на основе сигнала по скорости можно вычислить оптимальный угол смещения ДПР. Структурная схема вычислителя приведена на рис. 2.

Из уравнения (10) видно, что ΔМ возрастает с ростом U влияние Т Э и ω на ΔМ незначительно. Для оценки влияния угла установки на напряжение выполним аналогичный анализ:

K U = U_3K - U U_H ЭКС   H

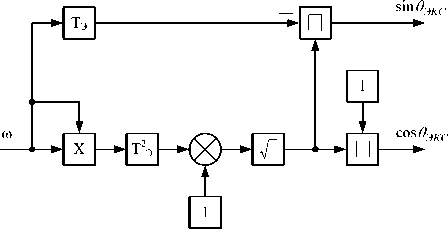
Рис. 2. Структурная схема вычислителя θ ЭКС

где U ЭКС – экстремальное значение U по формуле (5); U H – значение U из формулы (1) при условии θ =0.

к u = to + m (1 + T to ²)

V1 + T ₃ ² to ²

—

В реальном электроприводе экстремальный регулятор должен изменять сигналы ДПР по закону

Из уравнения (12) видно, что модуль ΔU возрастает с ростом ω , М и T Э . Определим чувствительность момента к изменениям напряжения и угла установки. Чувствительность к изменению напряжения определяется выражением:

_U dM U

= dU M

.

sin а = sin( a + 0 _ЭКС ) cos a ' = cos( a + 0 _ЭКС )

Для выполнения этих условий используем узел координатного преобразования. В вентильном двигателе имеются сигналы sin α и cos α , вырабатываемые ДПР. Сигналы sin θ ЭКС и cos θ ЭКС формируются вычислителем (рис. 2). На основании этого координатное преобразование

может быть реализовано схемой, структура которой приведена на рис. 3.

По структуре (рис. 1) было проведено моделирование вентильного двигателя. На рис. 4 приведены логарифмические амплитудные характеристики при управлении напряжением (1) и при управлении по углу установки (2).

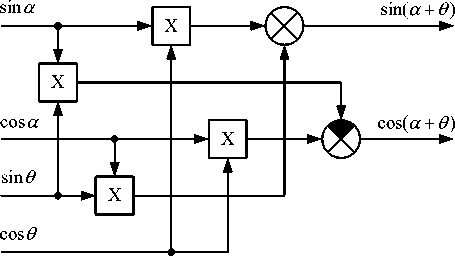
Рис. 3. Структурная схема узла координатного преобразования

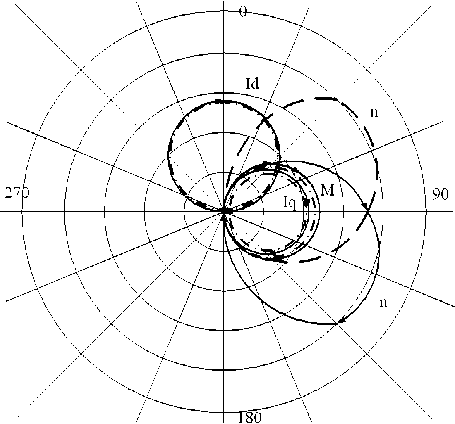
Рис. 4. Угловая диаграмма ВД

В процессе исследований анализировались координаты ВД при пуске с различными значениями угла Q . На основании этого построена угловая характеристика вентильного двигателя, изображенная на рис. 4. Изменение угла Q происходит по часовой стрелке. По направлениям значений угла Q в масштабе отложены соответствующие значения координат ВД, которые затем соединены в годограф. Положительные значения координаты обозначены непрерывистой линией, отрицательные – пунктирной.

Анализ угловой диаграммы (рис. 4) показывает, что

• -    годографы координат Id, Iq, M представляют собой окружности;

• -    годоргафы Id и Iq сдвинуты друг относительно друга на 90 градусов;

• -    годограф n состоит из двух эллипсов, экстремумы для +n и –n не совпадают, но симметричны относительно Q =90 ° ;

• -    годографы Iq и M лежат на одной оси и масштабно совпадают;

• -    максимальная скорость при пуске соответствует Q =90 ° ±а, где а - угол, зависящий от конструктивных параметров ВД.